Minimum Spanning Trees Prims Algorithm Kruskals Algorithm by

Minimum Spanning Trees • Prim’s Algorithm • Kruskal’s Algorithm by, Faraz Bagwan ME Comp. VIIT 521003

Contents • • Definition (MST) Prim’s Algorithm Walk-Through using graph. (Prim’s) Kruskal’s Algorithm Walk-Through using graph. (Kruskal’s) Difference Applications

Definition • A Minimum Spanning Tree (MST) is a subgraph of an undirected graph such that the subgraph spans (includes) all nodes, is connected, is acyclic, and has minimum total edge weight.

Algorithm Characteristics • Both Prim’s and Kruskal’s Algorithms work with undirected graphs • Both work with weighted and unweighted graphs but are more interesting when edges are weighted • Both are greedy algorithms that produce optimal solutions

Prim’s Algorithm • The idea behind Prim’s algorithm is simple, a spanning tree means all vertices must be connected. • So the two disjoint subsets of vertices must be connected to make a Spanning Tree. • And they must be connected with the minimum weight edge to make it a Minimum Spanning Tree.
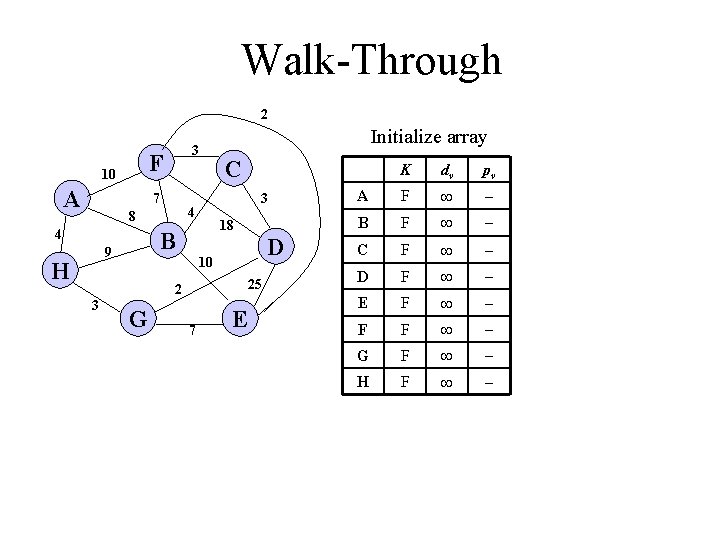
Walk-Through 2 F 10 A 3 7 4 H 18 B 9 C 3 4 8 Initialize array 25 2 3 D 10 G 7 E K dv pv A F B F C F D F E F F F G F H F
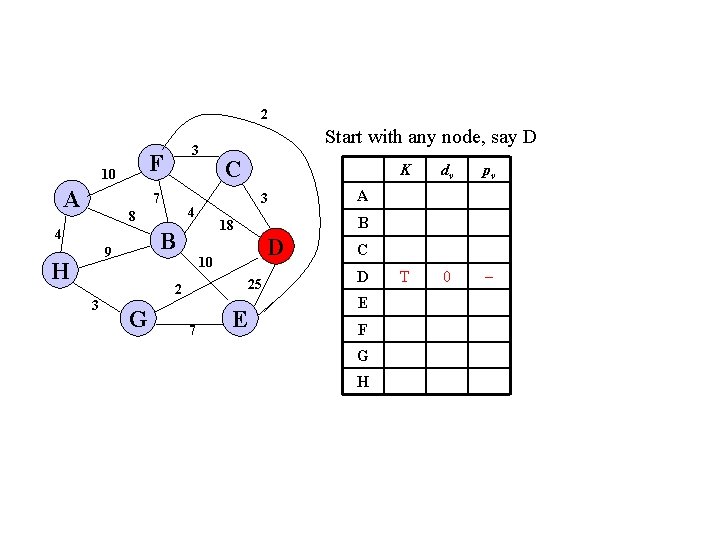
2 F 10 A 3 7 4 H 3 D 10 25 2 G 7 E K dv pv T 0 A B 18 B 9 C 3 4 8 Start with any node, say D C D E F G H
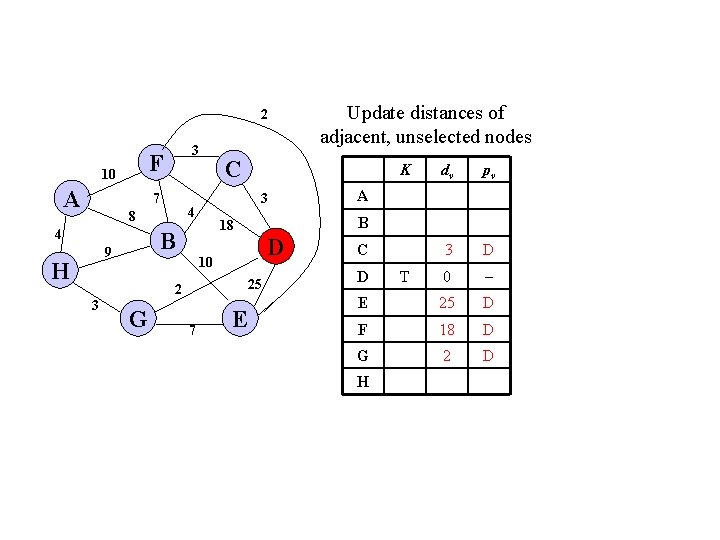
2 F 10 A 3 7 4 H G D 25 7 E dv pv 3 D 0 E 25 D F 18 D G 2 D A B 10 2 3 K 18 B 9 C 3 4 8 Update distances of adjacent, unselected nodes C D H T
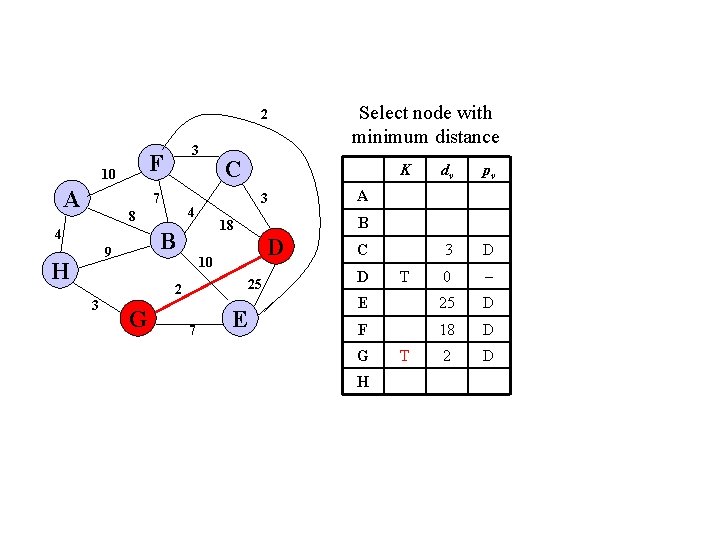
2 F 10 A 3 7 4 H G D 25 7 E dv pv 3 D 0 E 25 D F 18 D 2 D A B 10 2 3 K 18 B 9 C 3 4 8 Select node with minimum distance C D G H T T
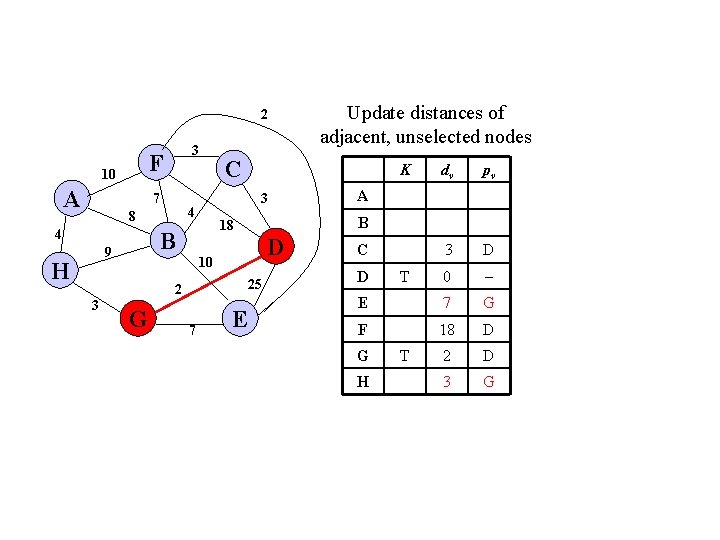
2 F 10 A 3 7 4 H G D 25 7 E dv pv 3 D 0 E 7 G F 18 D 2 D 3 G A B 10 2 3 K 18 B 9 C 3 4 8 Update distances of adjacent, unselected nodes C D G H T T
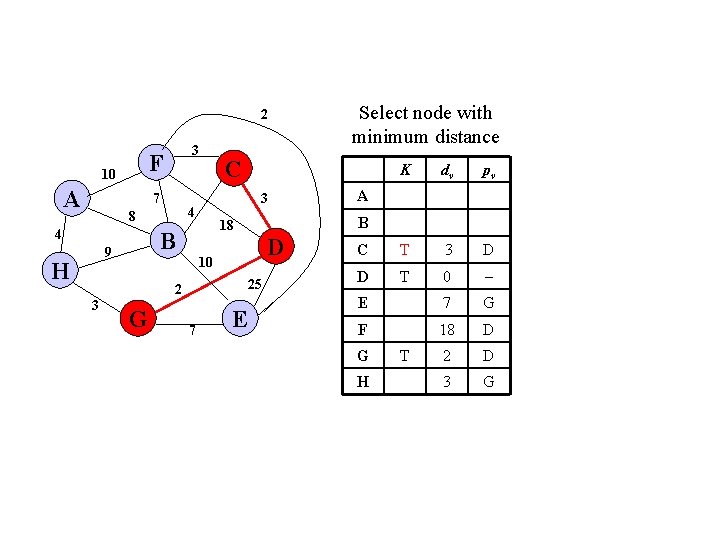
2 F 10 A 3 7 4 H 3 D 10 25 2 G 7 E K dv pv C T 3 D D T 0 E 7 G F 18 D 2 D 3 G A B 18 B 9 C 3 4 8 Select node with minimum distance G H T
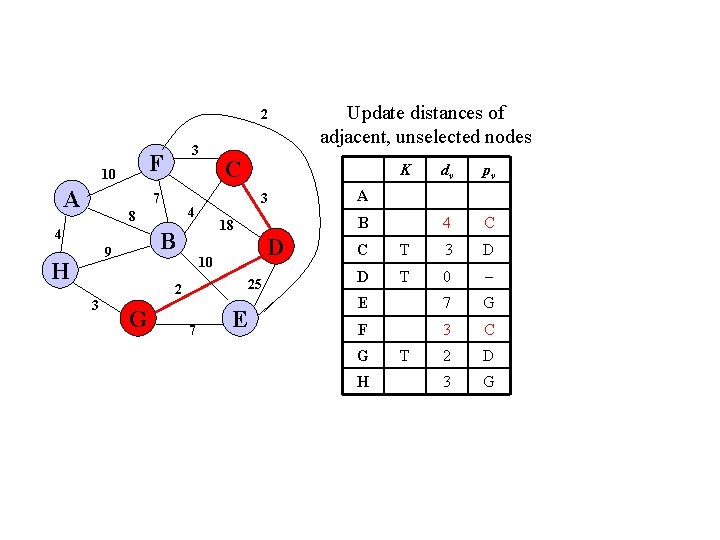
2 F 10 A 3 7 4 H D 25 G 7 E dv pv 4 C A B 10 2 3 K 18 B 9 C 3 4 8 Update distances of adjacent, unselected nodes C T 3 D D T 0 E 7 G F 3 C 2 D 3 G G H T
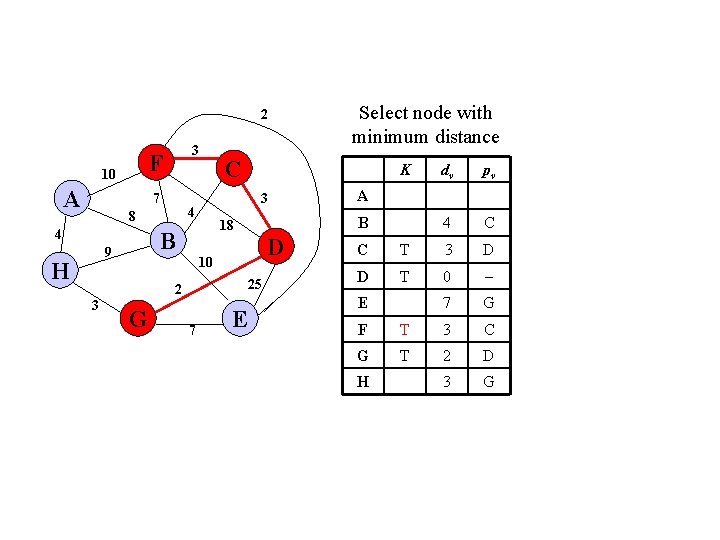
2 F 10 A 3 7 4 H D 25 G 7 E dv pv 4 C A B 10 2 3 K 18 B 9 C 3 4 8 Select node with minimum distance C T 3 D D T 0 7 G E F T 3 C G T 2 D 3 G H
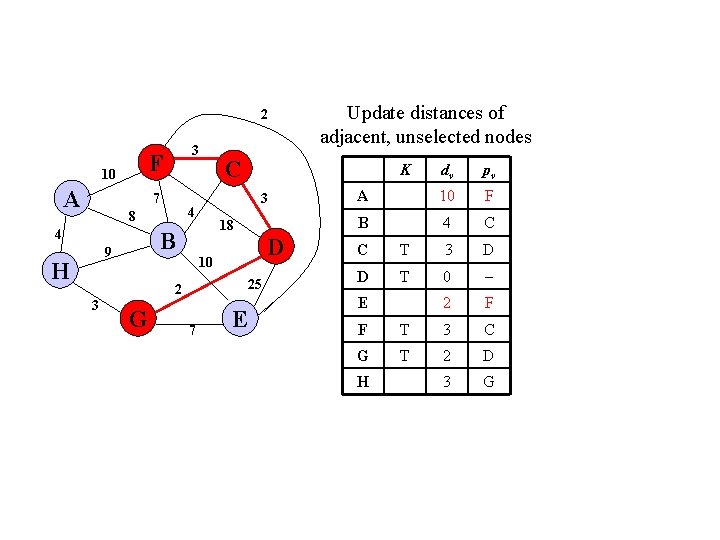
2 F 10 A 3 7 4 H D 10 25 2 3 K 18 B 9 C 3 4 8 G 7 Update distances of adjacent, unselected nodes E dv pv A 10 F B 4 C C T 3 D D T 0 2 F E F T 3 C G T 2 D 3 G H
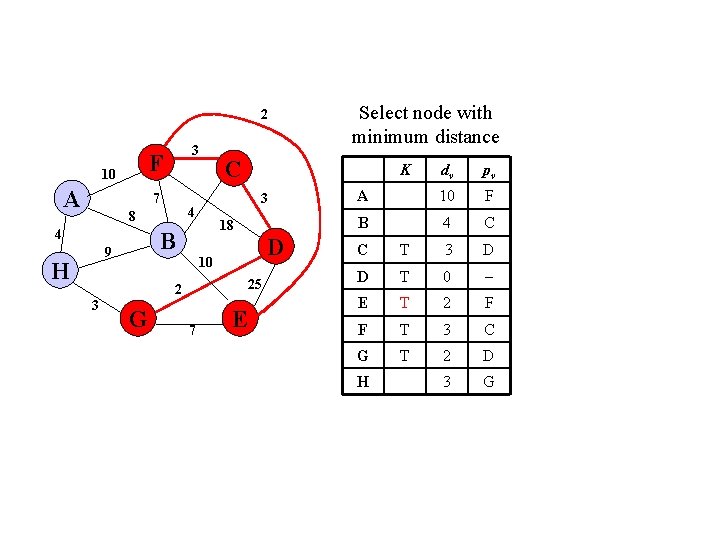
2 F 10 A 3 7 4 H D 10 25 2 3 K 18 B 9 C 3 4 8 G 7 Select node with minimum distance E dv pv A 10 F B 4 C C T 3 D D T 0 E T 2 F F T 3 C G T 2 D 3 G H
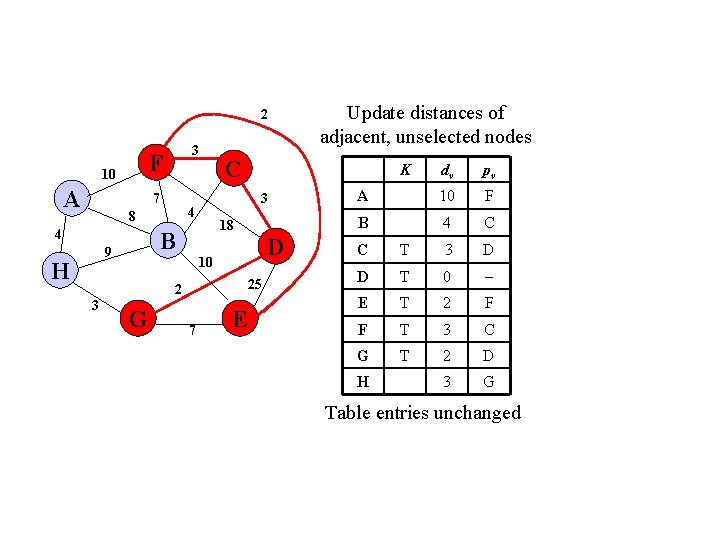
2 F 10 A 3 7 4 H D 10 25 2 3 K 18 B 9 C 3 4 8 G 7 Update distances of adjacent, unselected nodes E dv pv A 10 F B 4 C C T 3 D D T 0 E T 2 F F T 3 C G T 2 D 3 G H Table entries unchanged
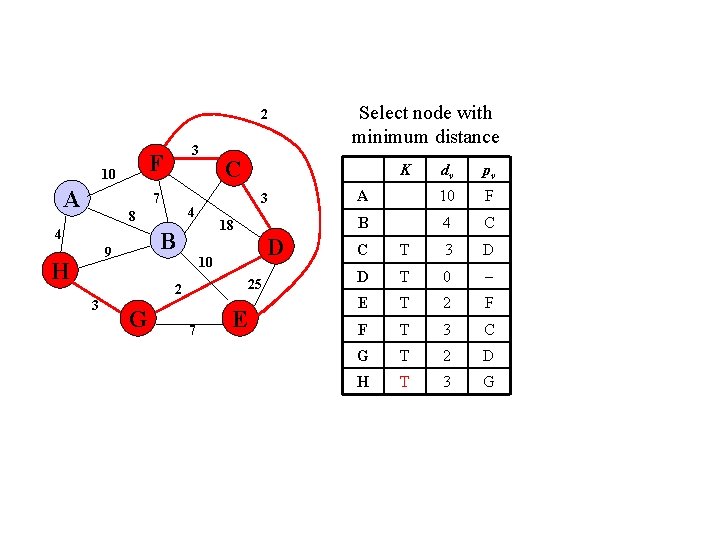
2 F 10 A 3 7 4 H D 10 25 2 3 K 18 B 9 C 3 4 8 G 7 Select node with minimum distance E dv pv A 10 F B 4 C C T 3 D D T 0 E T 2 F F T 3 C G T 2 D H T 3 G
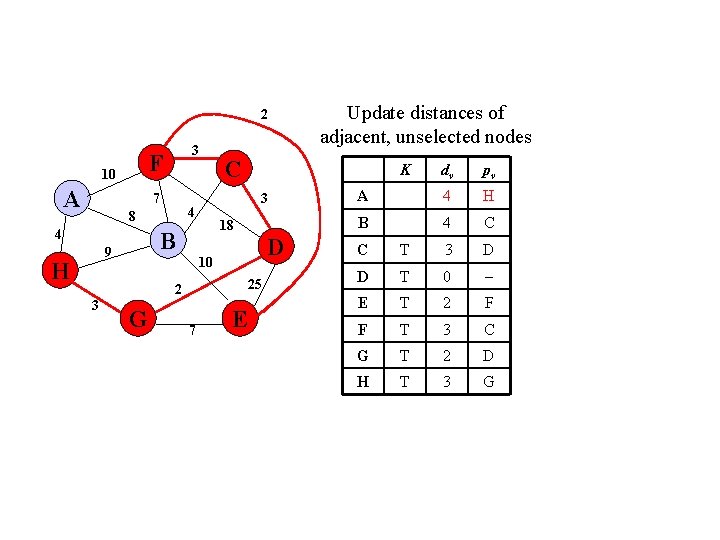
2 F 10 A 3 7 4 H D 10 25 2 3 K 18 B 9 C 3 4 8 G 7 Update distances of adjacent, unselected nodes E dv pv A 4 H B 4 C C T 3 D D T 0 E T 2 F F T 3 C G T 2 D H T 3 G
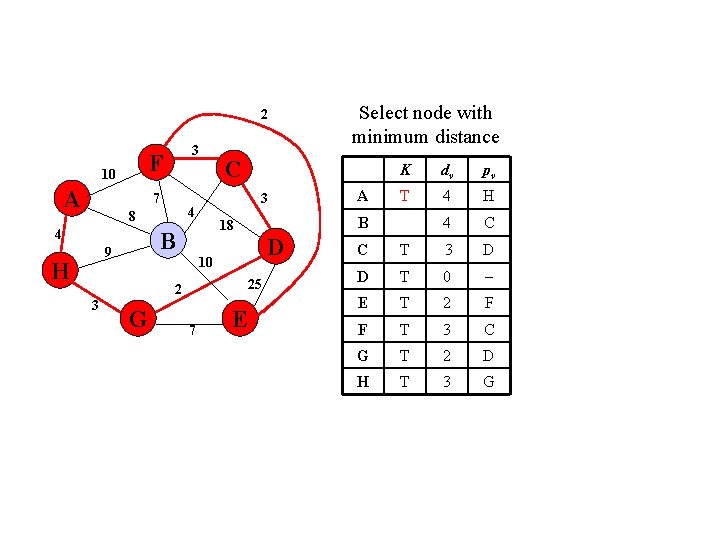
2 F 10 A 3 7 4 H 3 D 10 25 2 G 7 E A K dv pv T 4 H 4 C B 18 B 9 C 3 4 8 Select node with minimum distance C T 3 D D T 0 E T 2 F F T 3 C G T 2 D H T 3 G
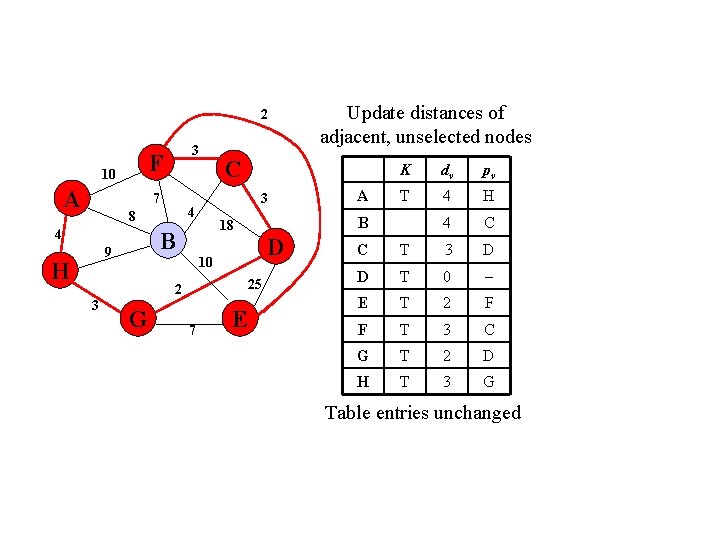
2 F 10 A 3 7 4 H 3 D 10 25 2 G 7 E A K dv pv T 4 H 4 C B 18 B 9 C 3 4 8 Update distances of adjacent, unselected nodes C T 3 D D T 0 E T 2 F F T 3 C G T 2 D H T 3 G Table entries unchanged
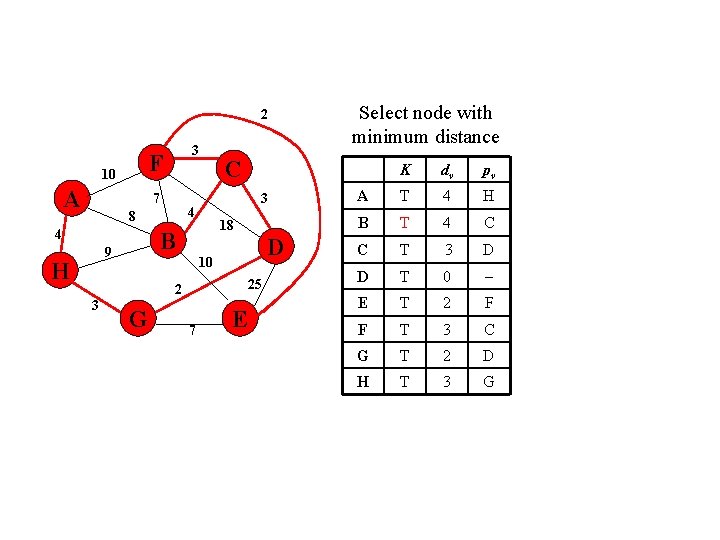
2 F 10 A 3 7 4 H 18 B 9 C 3 4 8 D 10 25 2 3 G 7 Select node with minimum distance E K dv pv A T 4 H B T 4 C C T 3 D D T 0 E T 2 F F T 3 C G T 2 D H T 3 G
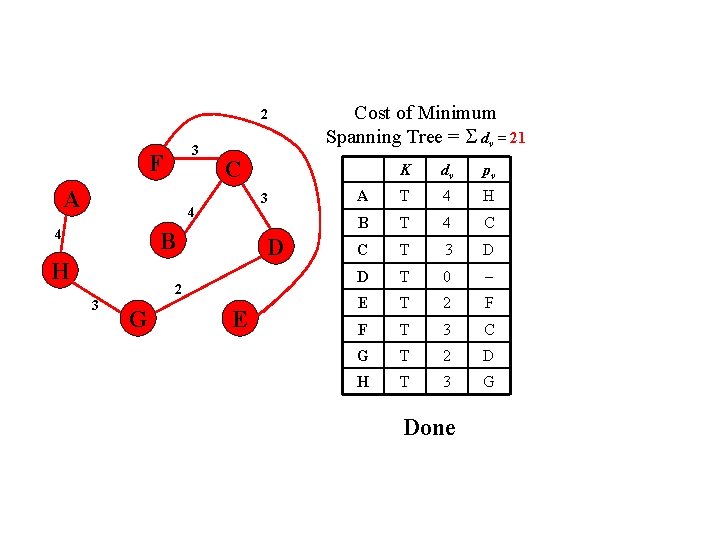
2 3 F A C 3 4 4 B H D 2 3 G Cost of Minimum Spanning Tree = dv = 21 E K dv pv A T 4 H B T 4 C C T 3 D D T 0 E T 2 F F T 3 C G T 2 D H T 3 G Done

Pseudo code 1. Make a queue (Q) with all the vertices of G (V); 2. For each member of Q set the priority to INFINITY; 3. Only for the starting vertex (s) set the priority to 0; 4. The parent of (s) should be NULL; 5. While Q isn’t empty 6. Get the minimum from Q – let’s say (u); (priority queue); 7. For each adjacent vertex to (v) to (u) 8. If (v) is in Q and weight of (u, v) < priority of (v) then 9. The parent of (v) is set to be (u) 10. The priority of (v) is the weight of (u, v)

Prim’s Time Complexity • O(V^2). • If the input graph is represented using adjacency list, then the time complexity of Prim’s algorithm can be reduced to O(E log V) with the help of binary heap.

Kruskal’s Algorithm • Works with edges, rather than nodes • Steps: – Sort edges by increasing edge weight. – Pick the smallest edge. Check if it forms a cycle with the spanning tree formed so far. If cycle is not formed, include this edge. Else, discard it. – Repeat step#2 until there are (V-1) edges in the spanning tree.
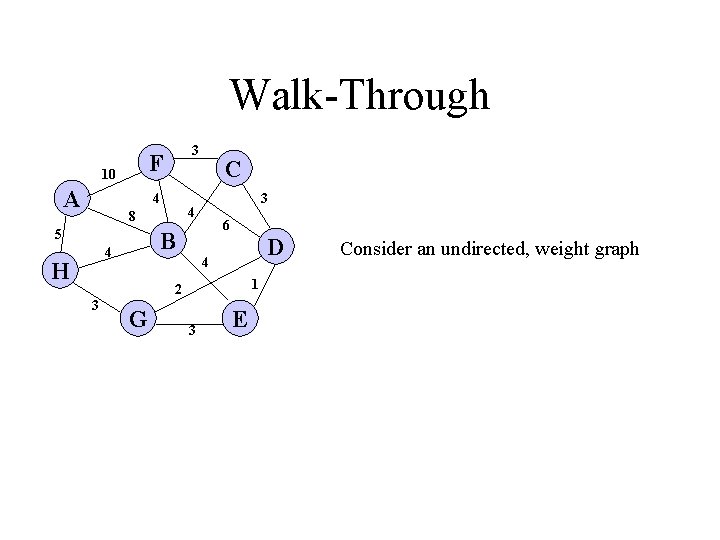
Walk-Through F 10 A 3 4 6 B 4 H 3 4 8 5 C D 4 1 2 3 G 3 E Consider an undirected, weight graph
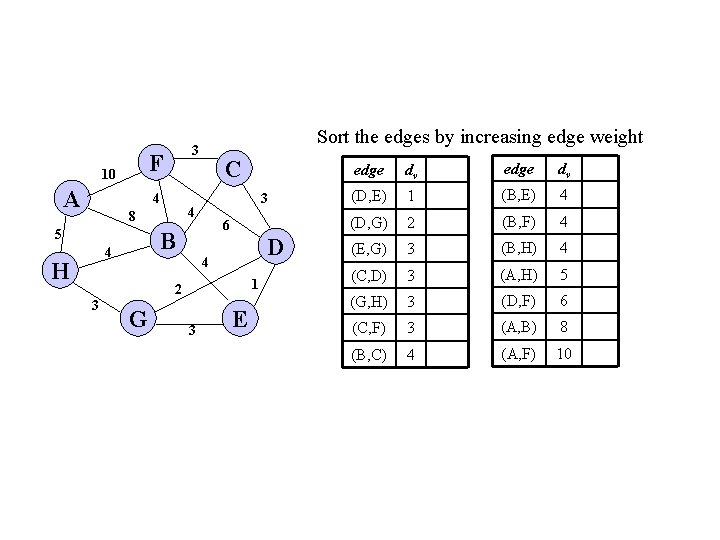
F 10 A 4 3 6 B 4 H C 4 8 5 Sort the edges by increasing edge weight 3 D 4 1 2 3 G 3 E edge dv (D, E) 1 (B, E) 4 (D, G) 2 (B, F) 4 (E, G) 3 (B, H) 4 (C, D) 3 (A, H) 5 (G, H) 3 (D, F) 6 (C, F) 3 (A, B) 8 (B, C) 4 (A, F) 10
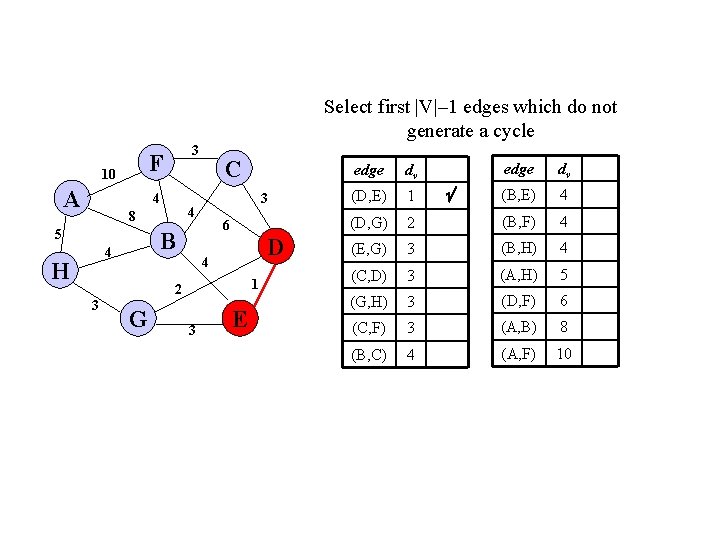
Select first |V|– 1 edges which do not generate a cycle F 10 A 3 4 6 B 4 H 3 4 8 5 C D 4 1 2 3 G 3 E edge dv (B, E) 4 2 (B, F) 4 (E, G) 3 (B, H) 4 (C, D) 3 (A, H) 5 (G, H) 3 (D, F) 6 (C, F) 3 (A, B) 8 (B, C) 4 (A, F) 10 edge dv (D, E) 1 (D, G)
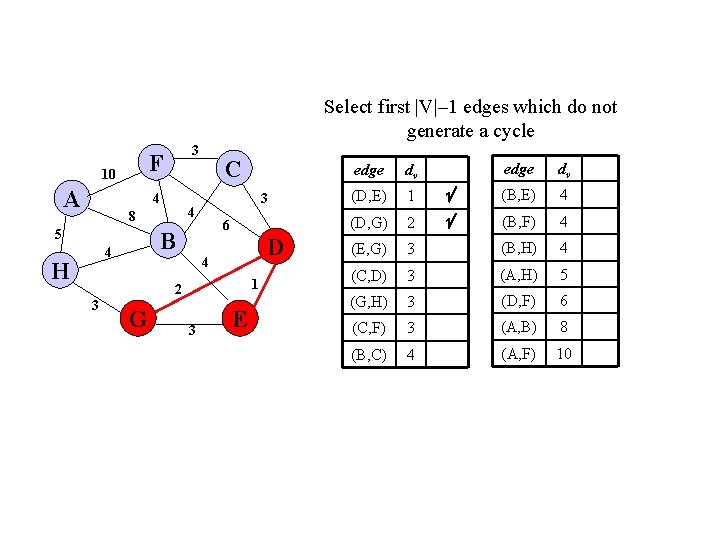
Select first |V|– 1 edges which do not generate a cycle F 10 A 3 4 6 B 4 H 3 4 8 5 C D 4 1 2 3 G 3 E edge dv (B, E) 4 (B, F) 4 3 (B, H) 4 (C, D) 3 (A, H) 5 (G, H) 3 (D, F) 6 (C, F) 3 (A, B) 8 (B, C) 4 (A, F) 10 edge dv (D, E) 1 (D, G) 2 (E, G)
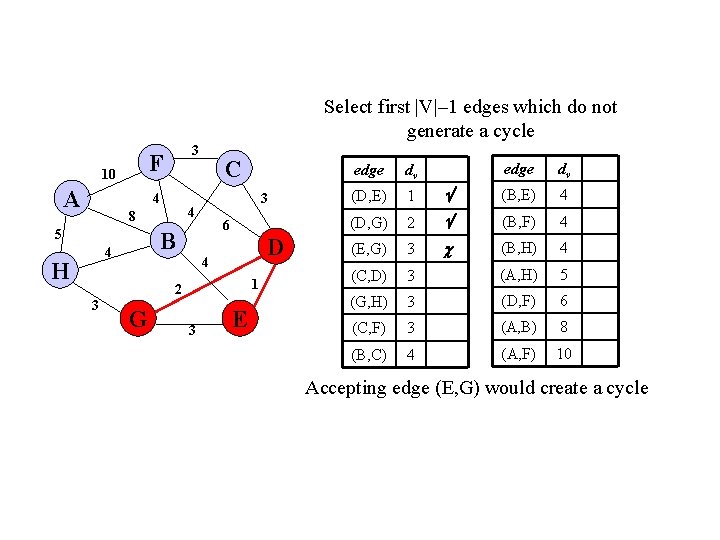
Select first |V|– 1 edges which do not generate a cycle F 10 A 3 4 6 B 4 H 3 4 8 5 C D 4 1 2 3 G 3 E edge dv (B, E) 4 2 (B, F) 4 (E, G) 3 (B, H) 4 (C, D) 3 (A, H) 5 (G, H) 3 (D, F) 6 (C, F) 3 (A, B) 8 (B, C) 4 (A, F) 10 edge dv (D, E) 1 (D, G) Accepting edge (E, G) would create a cycle
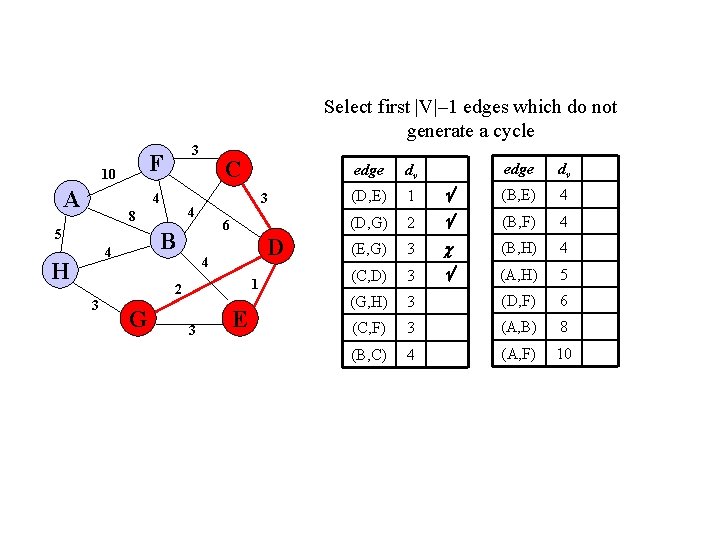
Select first |V|– 1 edges which do not generate a cycle F 10 A 3 4 6 B 4 H 3 4 8 5 C D 4 1 2 3 G 3 E edge dv (B, E) 4 2 (B, F) 4 (E, G) 3 (B, H) 4 (C, D) 3 (A, H) 5 (G, H) 3 (D, F) 6 (C, F) 3 (A, B) 8 (B, C) 4 (A, F) 10 edge dv (D, E) 1 (D, G)
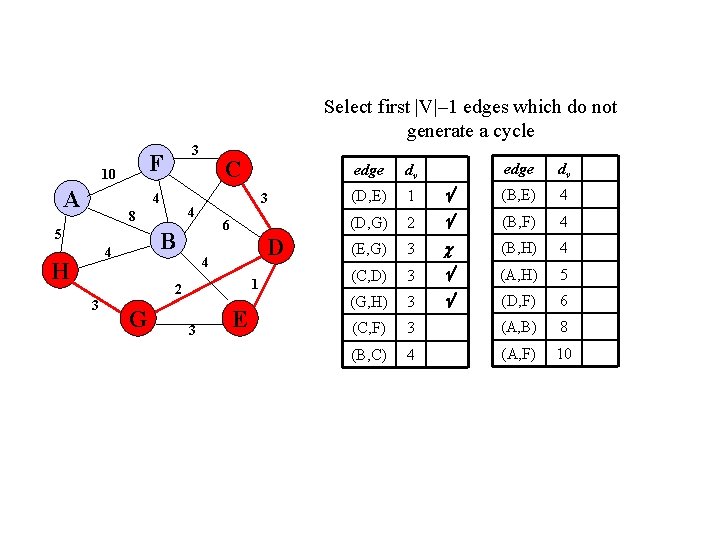
Select first |V|– 1 edges which do not generate a cycle F 10 A 3 4 6 B 4 H 3 4 8 5 C D 4 1 2 3 G 3 E edge dv (B, E) 4 2 (B, F) 4 (E, G) 3 (B, H) 4 (C, D) 3 (A, H) 5 (G, H) 3 (D, F) 6 (C, F) 3 (A, B) 8 (B, C) 4 (A, F) 10 edge dv (D, E) 1 (D, G)
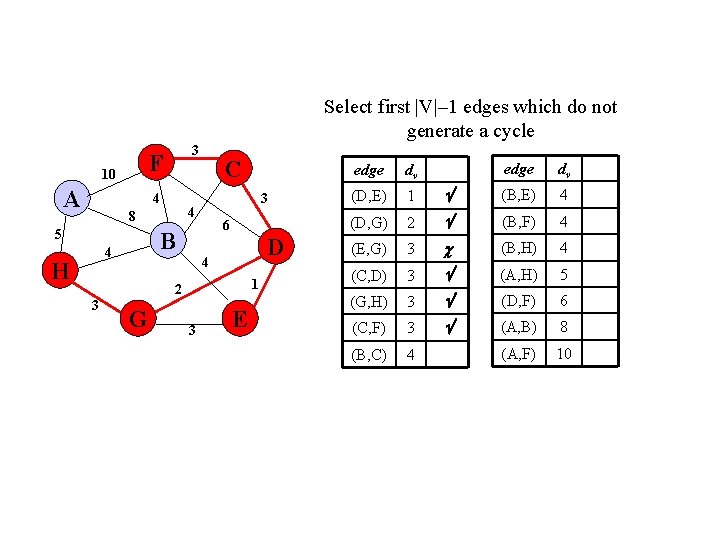
Select first |V|– 1 edges which do not generate a cycle F 10 A 3 4 6 B 4 H 3 4 8 5 C D 4 1 2 3 G 3 E edge dv (B, E) 4 2 (B, F) 4 (E, G) 3 (B, H) 4 (C, D) 3 (A, H) 5 (G, H) 3 (D, F) 6 (C, F) 3 (A, B) 8 (B, C) 4 (A, F) 10 edge dv (D, E) 1 (D, G)
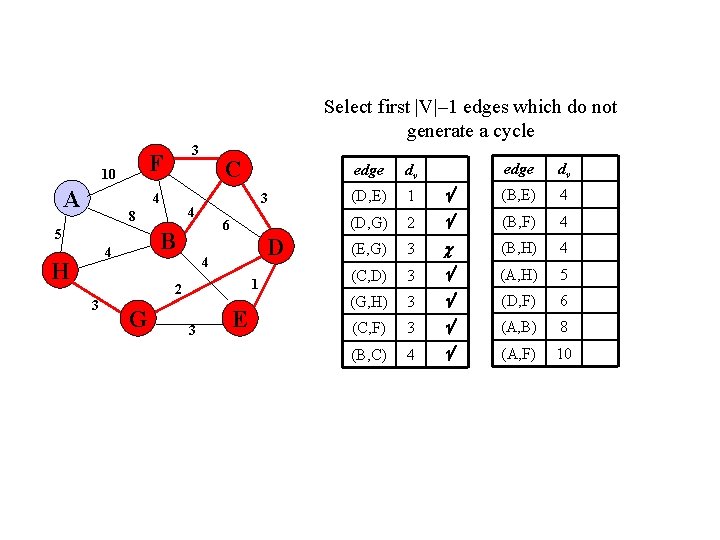
Select first |V|– 1 edges which do not generate a cycle F 10 A 3 4 6 B 4 H 3 4 8 5 C D 4 1 2 3 G 3 E edge dv (B, E) 4 2 (B, F) 4 (E, G) 3 (B, H) 4 (C, D) 3 (A, H) 5 (G, H) 3 (D, F) 6 (C, F) 3 (A, B) 8 (B, C) 4 (A, F) 10 edge dv (D, E) 1 (D, G)
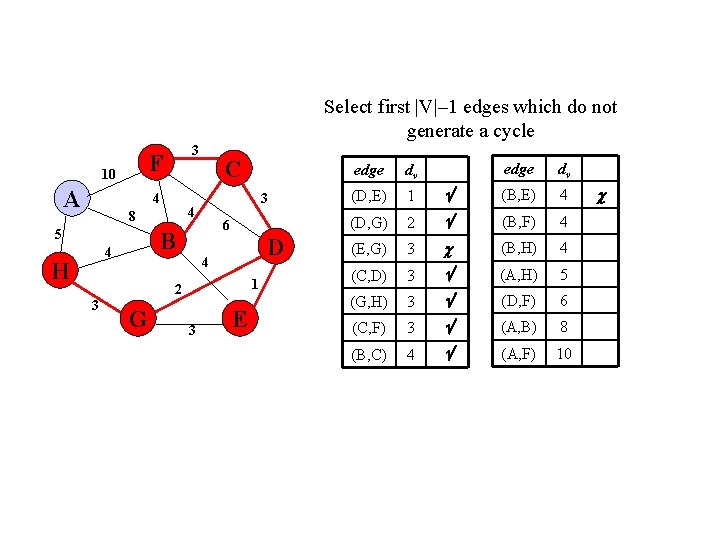
Select first |V|– 1 edges which do not generate a cycle F 10 A 3 4 6 B 4 H 3 4 8 5 C D 4 1 2 3 G 3 E edge dv (B, E) 4 2 (B, F) 4 (E, G) 3 (B, H) 4 (C, D) 3 (A, H) 5 (G, H) 3 (D, F) 6 (C, F) 3 (A, B) 8 (B, C) 4 (A, F) 10 edge dv (D, E) 1 (D, G)
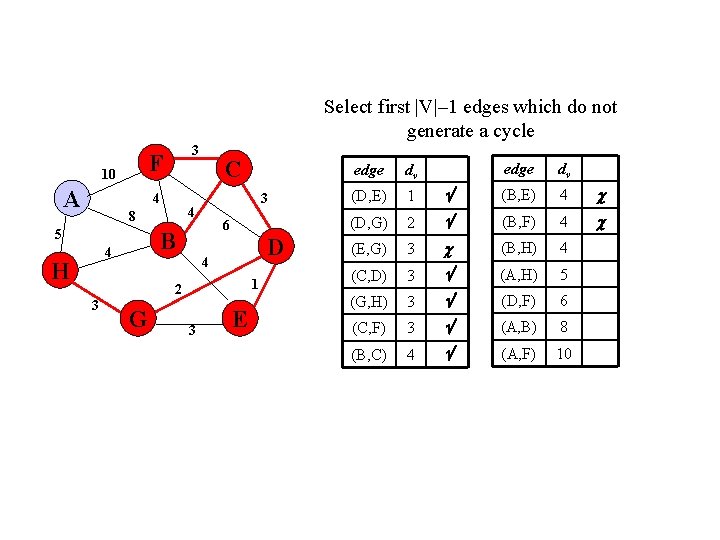
Select first |V|– 1 edges which do not generate a cycle F 10 A 3 4 6 B 4 H 3 4 8 5 C D 4 1 2 3 G 3 E edge dv (B, E) 4 2 (B, F) 4 (E, G) 3 (B, H) 4 (C, D) 3 (A, H) 5 (G, H) 3 (D, F) 6 (C, F) 3 (A, B) 8 (B, C) 4 (A, F) 10 edge dv (D, E) 1 (D, G)
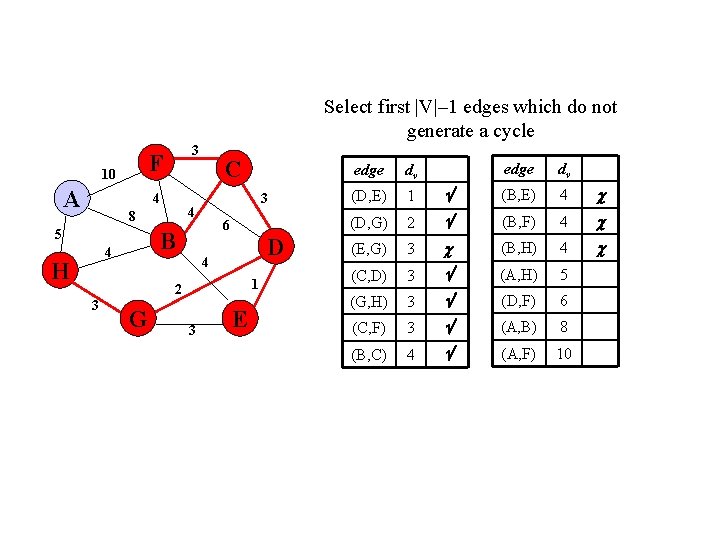
Select first |V|– 1 edges which do not generate a cycle F 10 A 3 4 6 B 4 H 3 4 8 5 C D 4 1 2 3 G 3 E edge dv (B, E) 4 2 (B, F) 4 (E, G) 3 (B, H) 4 (C, D) 3 (A, H) 5 (G, H) 3 (D, F) 6 (C, F) 3 (A, B) 8 (B, C) 4 (A, F) 10 edge dv (D, E) 1 (D, G)
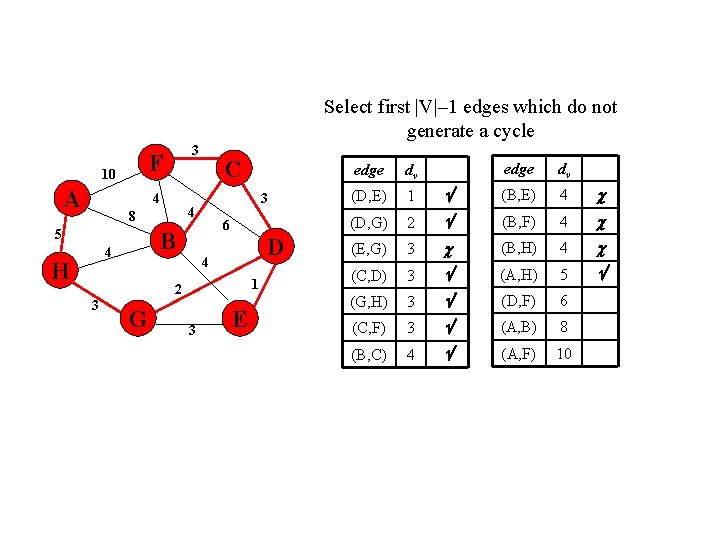
Select first |V|– 1 edges which do not generate a cycle F 10 A 3 4 6 B 4 H 3 4 8 5 C D 4 1 2 3 G 3 E edge dv (B, E) 4 2 (B, F) 4 (E, G) 3 (B, H) 4 (C, D) 3 (A, H) 5 (G, H) 3 (D, F) 6 (C, F) 3 (A, B) 8 (B, C) 4 (A, F) 10 edge dv (D, E) 1 (D, G)
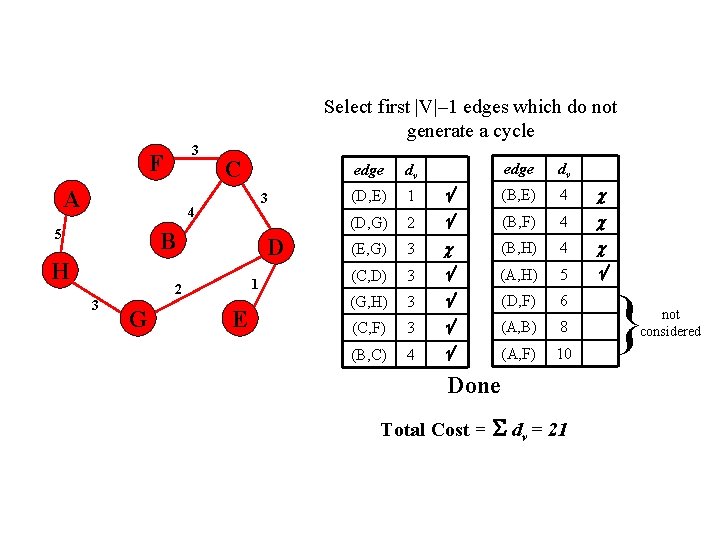
Select first |V|– 1 edges which do not generate a cycle 3 F A C 3 4 5 B H D 1 2 3 G E edge dv (B, E) 4 2 (B, F) 4 (E, G) 3 (B, H) 4 (C, D) 3 (A, H) 5 (G, H) 3 (D, F) 6 (C, F) 3 (A, B) 8 (B, C) 4 (A, F) 10 edge dv (D, E) 1 (D, G) Done Total Cost = dv = 21 } not considered

Pseudo code 1. 2. 3. 4. T (the final spanning tree) is defined to be the empty set; For each vertex v of G, make the empty set out of v; Sort the edges of G in ascending (non-decreasing) order; For each edge (u, v) from the stored list of step 3. If u and v belong to different sets Add (u, v) to T; Get together u and v in one single set; 5. Return T

Kruskal’s Time Complexity • O(Elog. E) or O(Elog. V). • Sorting of edges takes O(ELog. E) time. • After sorting, we iterate through all edges & apply findunion algorithm, so O(Log. V). • Overall complexity is O(ELog. E + ELog. V) • The value of E can be atmost V^2, so O(Log. V) are O(Log. E) same. • Therefore, overall time complexity is O(Elog. E) or O(Elog. V)

Difference b/w Prim’s & Kruskal’s • The basic difference the edge you choose next, to add to the spanning tree in each step. • In Prim's, you always keep a connected component, starting with a single vertex. You look at all edges from the current component to other vertices and find the smallest among them. You then add the neighbouring vertex to the component, increasing its size by 1. In N-1 steps, every vertex would be merged to the current one if we have a connected graph.

• In Kruskal's, you do not keep one connected component but a forest. At each stage, you look at the globally smallest edge that does not create a cycle in the current forest. Such an edge has to necessarily merge two trees in the current forest into one. Since you start with N singlevertex trees, in N-1 steps, they would all have merged into one if the graph was connected. Kruskal's has a larger complexity than Prim.

Applications • • Topology Cartography Geometry Clustering Routing Algorithms Generation of Mazes Mechanical / Electrical / Computer Networks Study of Molecular bonds in Chemistry

References • “data structures and algorithm analysis in c++”, Mark Allen Weiss, Ch. 9, topic 9. 5 • “Fundamentals of computer algorithms”, Ellis horowitz Sartaj Sahni, Ch. 4, topic 4. 6
- Slides: 45