Minimum Spanning Trees GHS Algorithm 1 Weighted Graph

Minimum Spanning Trees GHS Algorithm 1

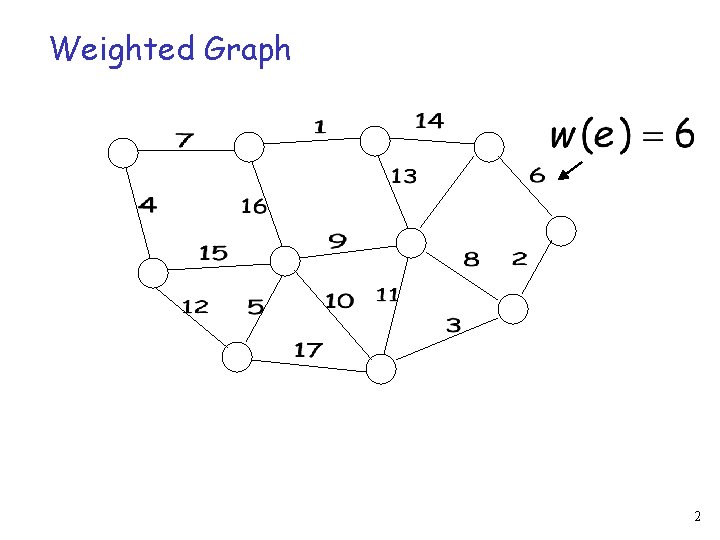
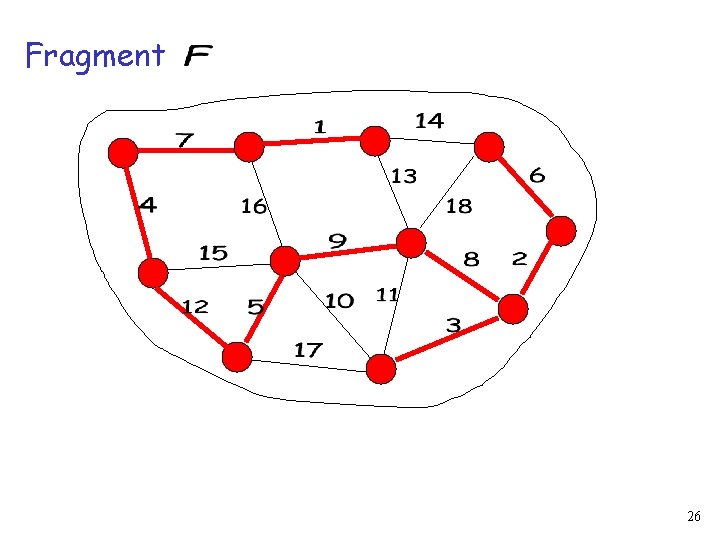
Weighted Graph 2

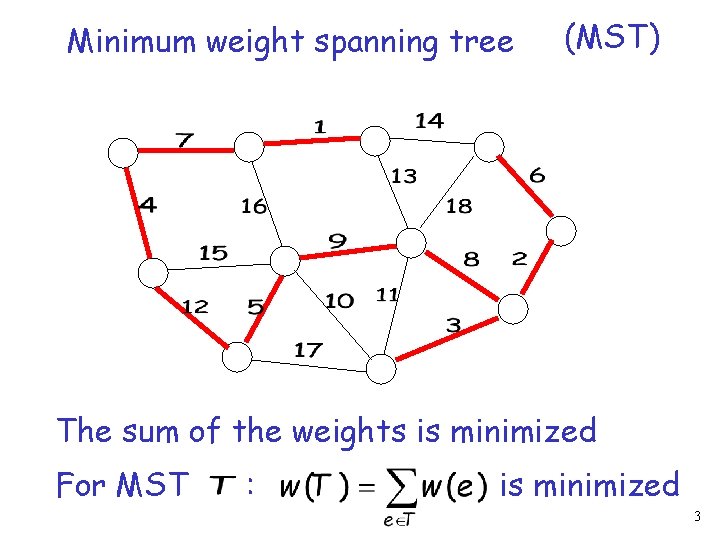
Minimum weight spanning tree (MST) The sum of the weights is minimized For MST : is minimized 3

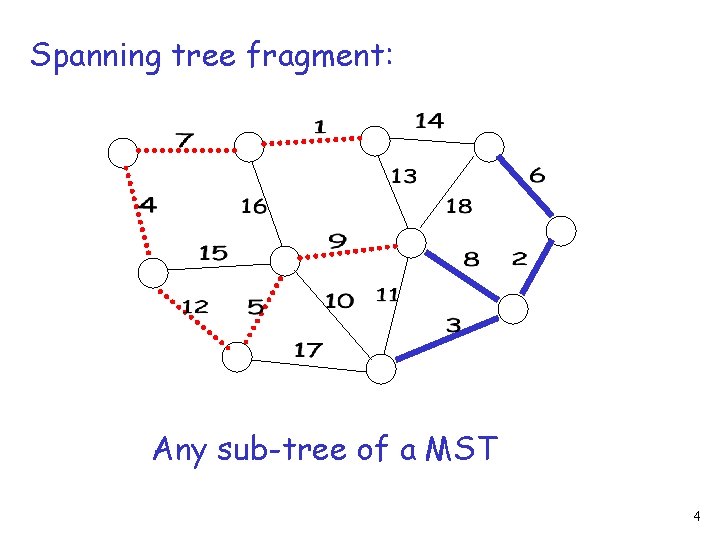
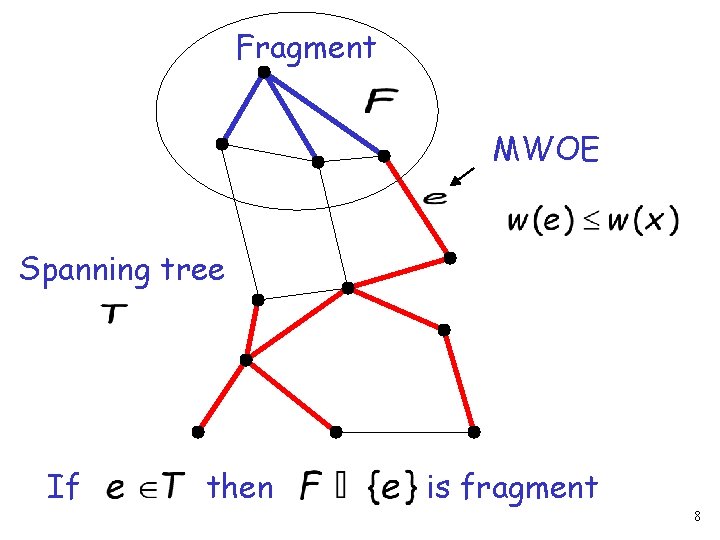
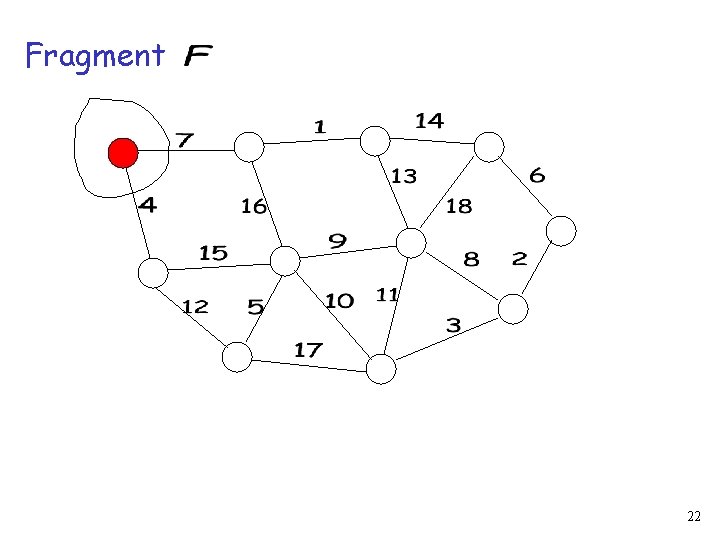
Spanning tree fragment: Any sub-tree of a MST 4

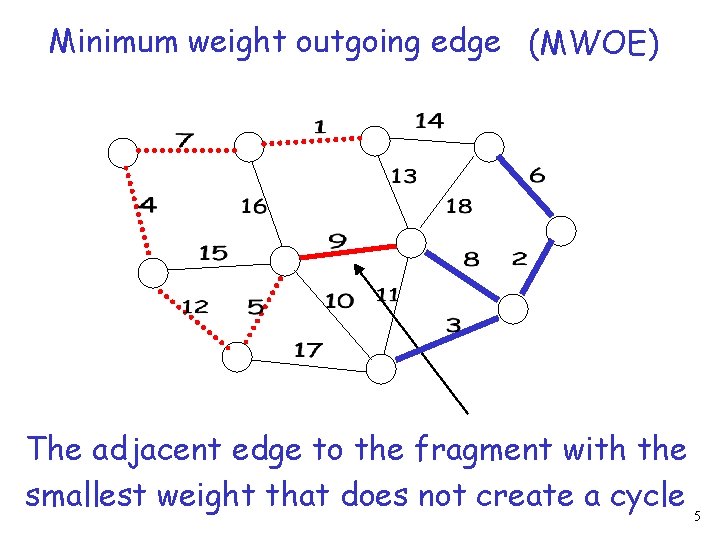
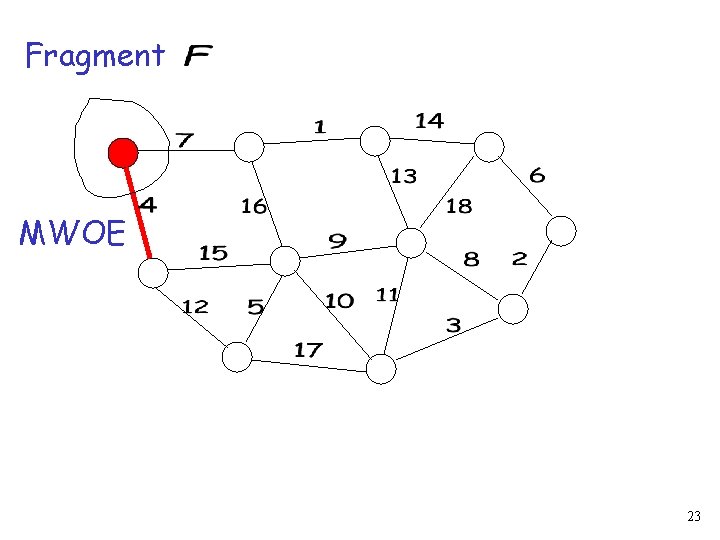
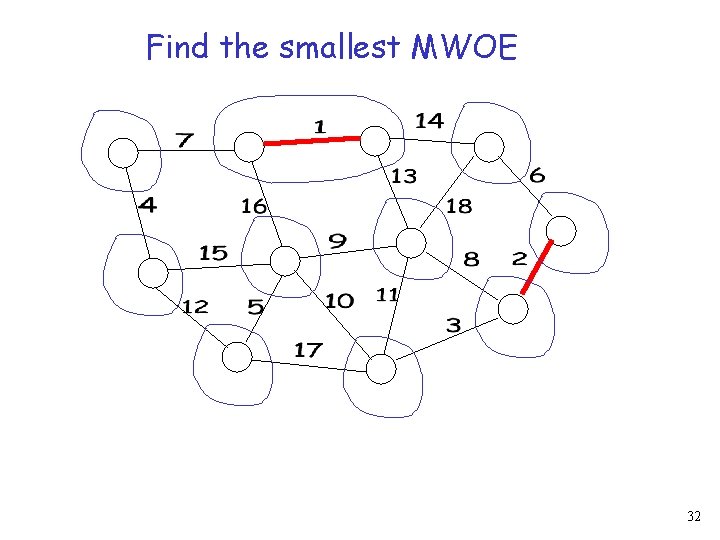
Minimum weight outgoing edge (MWOE) The adjacent edge to the fragment with the smallest weight that does not create a cycle 5

Two important properties for building MST Property 1: The union of a fragment and the MWOE is a fragment Property 2: If the weights are unique then the MST is unique 6

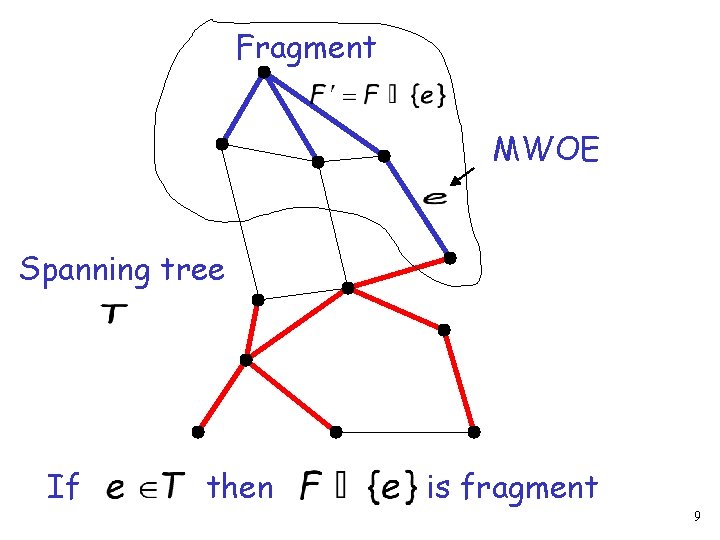
Property 1: The union of a fragment and the MWOE is a fragment Proof: Basic idea Examine if the new fragment is part of a MST 7

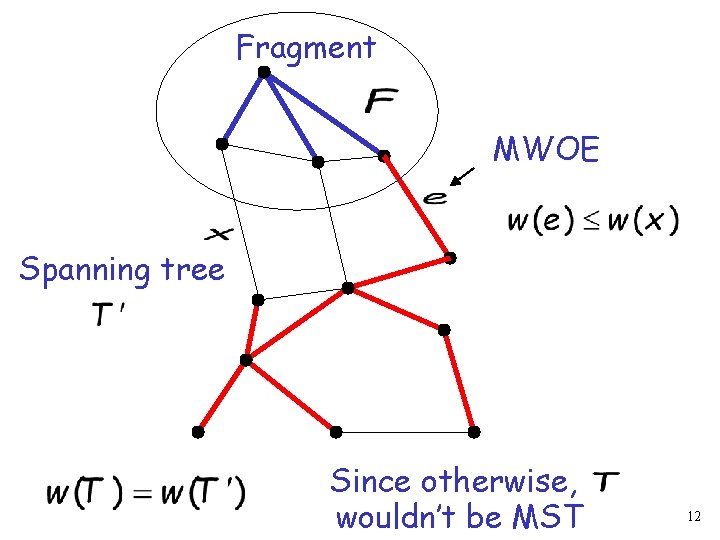
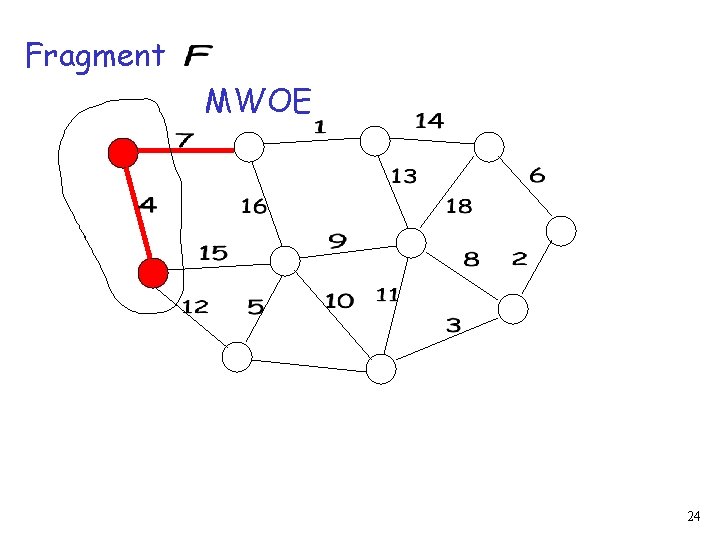
Fragment MWOE Spanning tree If then is fragment 8

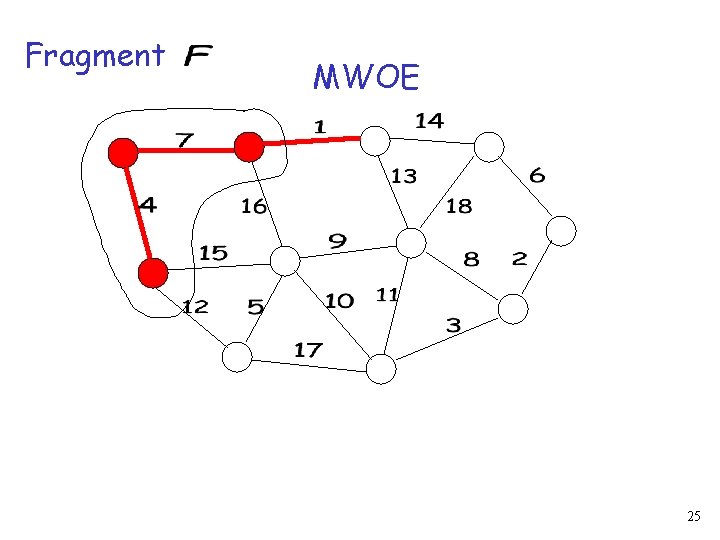
Fragment MWOE Spanning tree If then is fragment 9

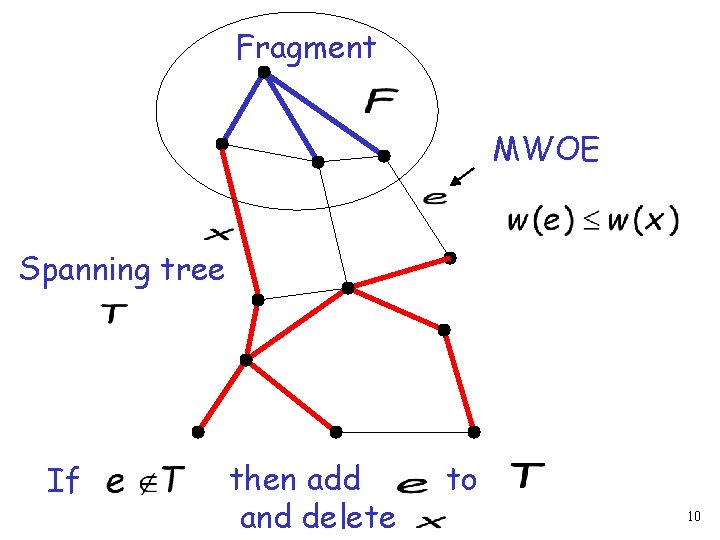
Fragment MWOE Spanning tree If then add and delete to 10

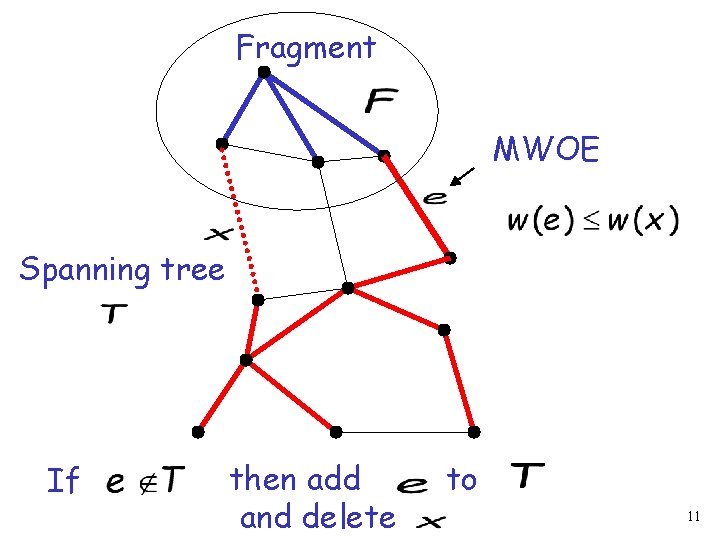
Fragment MWOE Spanning tree If then add and delete to 11

Fragment MWOE Spanning tree Since otherwise, wouldn’t be MST 12

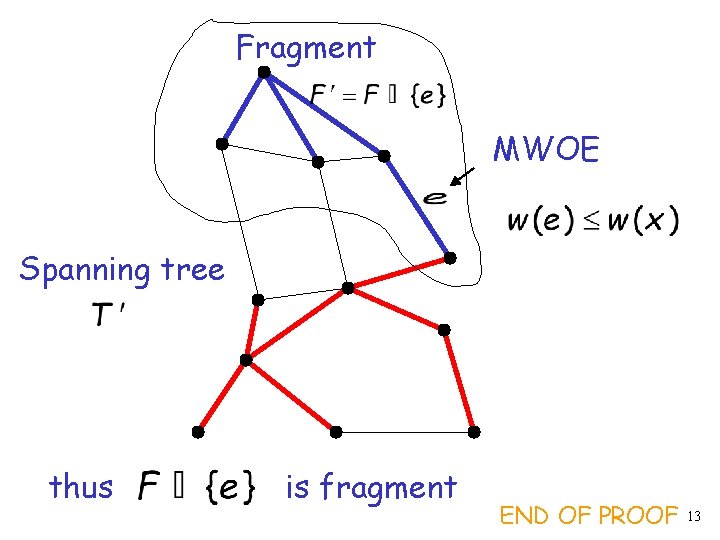
Fragment MWOE Spanning tree thus is fragment END OF PROOF 13

Property 2: If the weights are unique then the MST is unique Proof: Basic Idea: Suppose there are two MST Then there is another MST of smaller weight Contradiction! 14

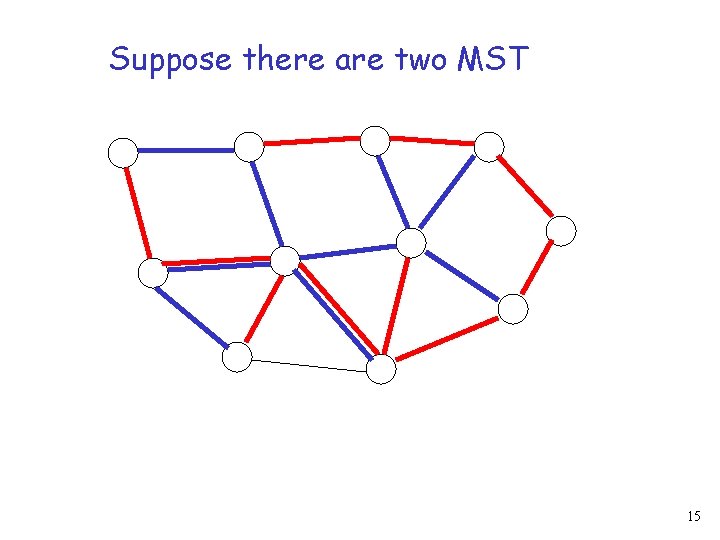
Suppose there are two MST 15

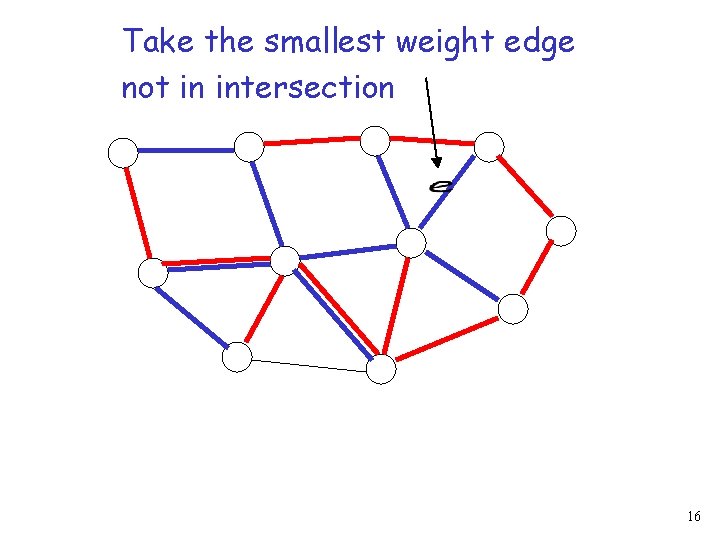
Take the smallest weight edge not in intersection 16

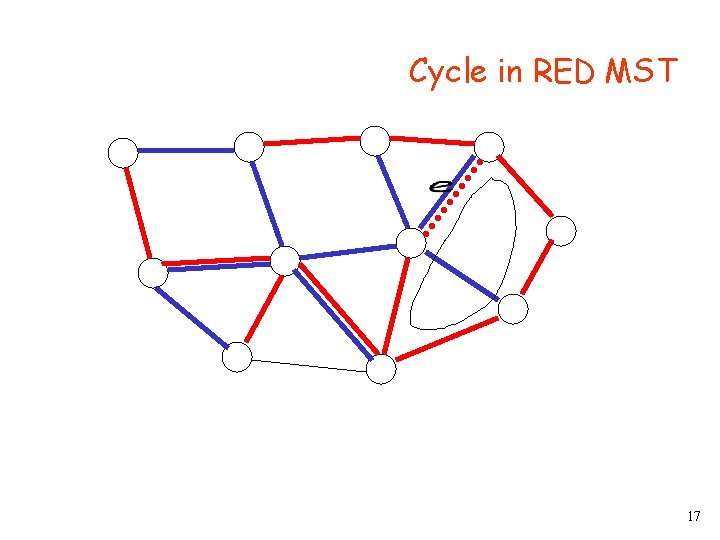
Cycle in RED MST 17

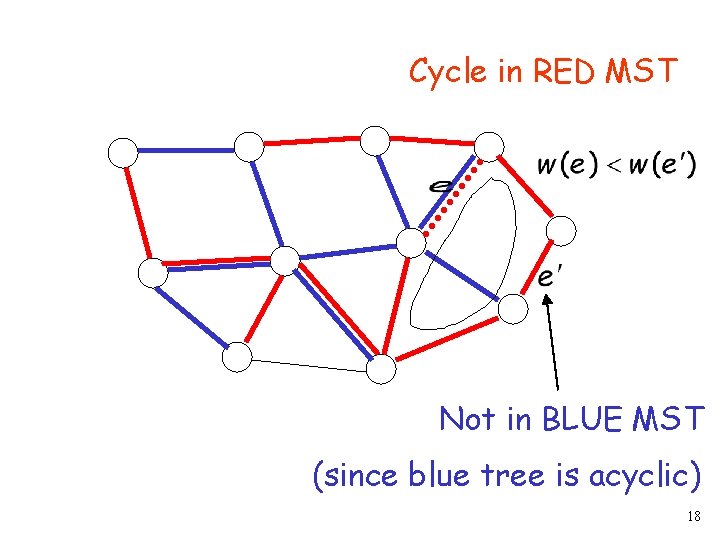
Cycle in RED MST Not in BLUE MST (since blue tree is acyclic) 18

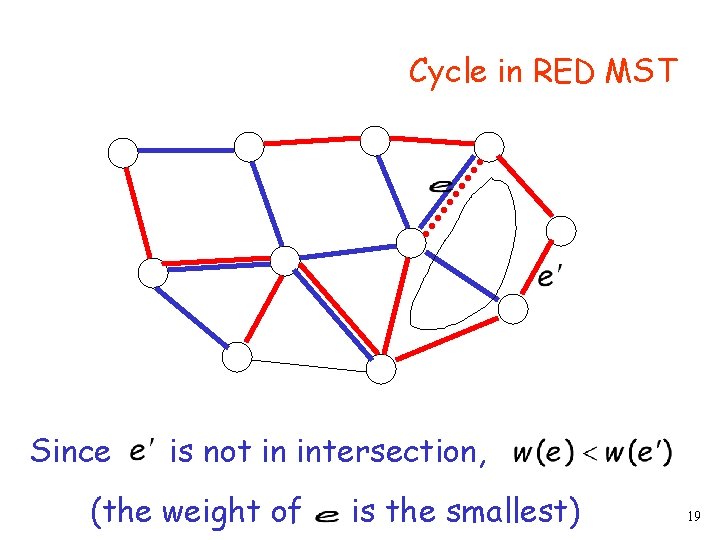
Cycle in RED MST Since is not in intersection, (the weight of is the smallest) 19

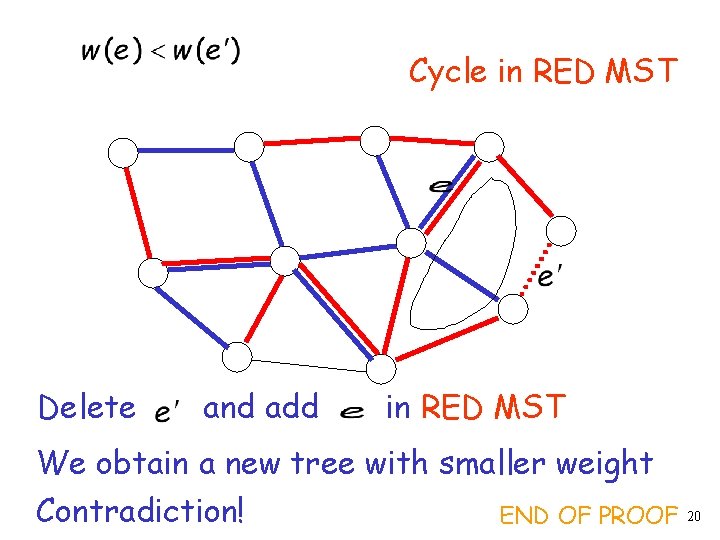
Cycle in RED MST Delete and add in RED MST We obtain a new tree with smaller weight Contradiction! END OF PROOF 20

Prim’s Algorithm Start with a node as an initial fragment Repeat Augment fragment with the MWOE Until no other edge can be added to (Assume unique IDs) 21

Fragment 22

Fragment MWOE 23

Fragment MWOE 24

Fragment MWOE 25

Fragment 26

Theorem: Proof: Prim’s algorithm gives an MST Use Property 1 repeatedly END OF PROOF 27

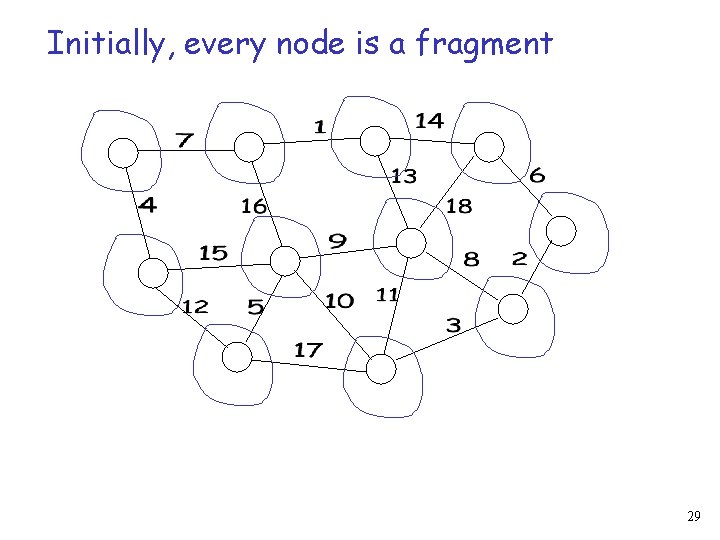
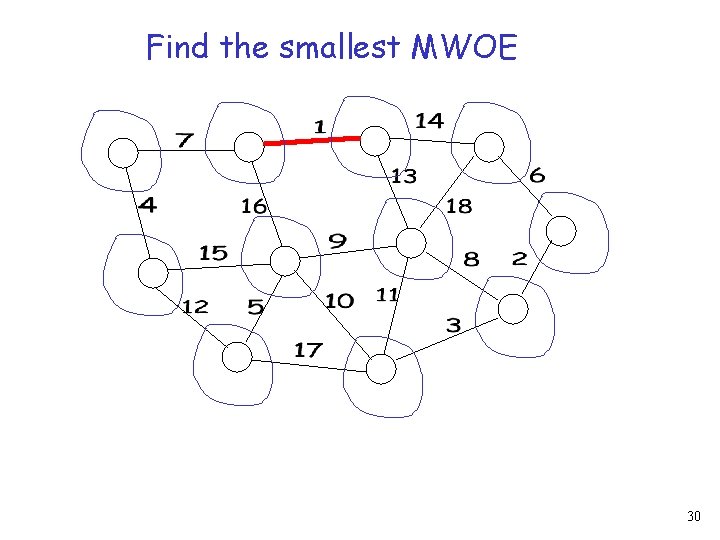
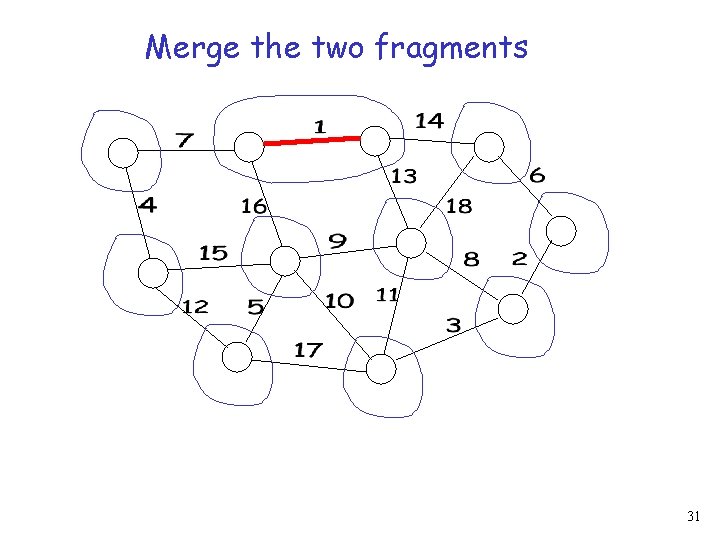
Kruskal’s Algorithm Initially, each node is a fragment Repeat Find the smallest MWOE of all fragments Merge the two fragments adjacent to Until there is one fragment (Assume unique IDs) 28

Initially, every node is a fragment 29

Find the smallest MWOE 30

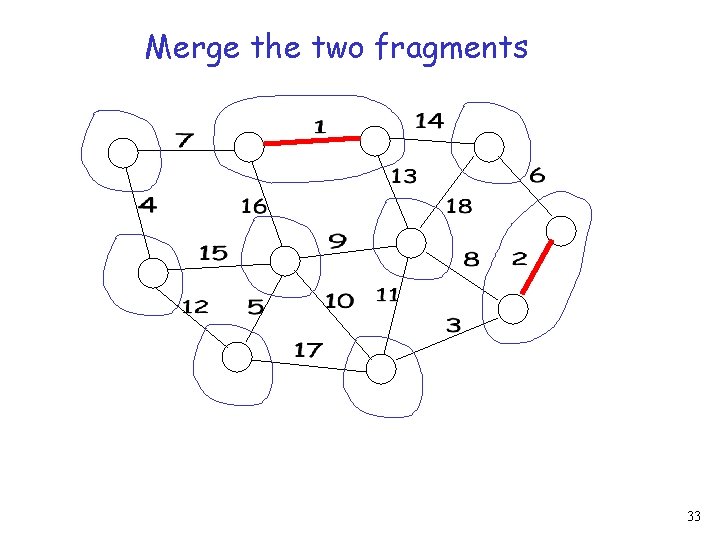
Merge the two fragments 31

Find the smallest MWOE 32

Merge the two fragments 33

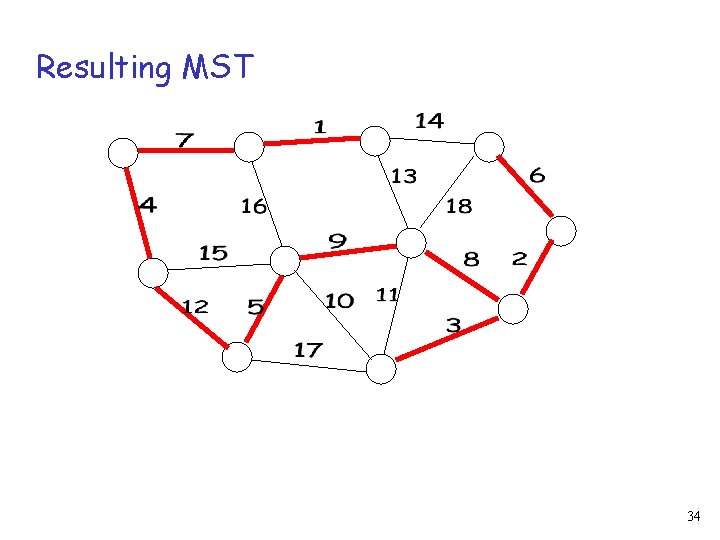
Resulting MST 34

Theorem: Proof: Kruskal’s algorithm gives an MST Use Properties 1 and 2 repeatedly Property 2 guarantees that the merged trees are fragments END OF PROOF 35

GHS Algorithm Distributed version of Kruskal’s Algorithm Initially, each node is a fragment Repeat in parallel: (A Synchronous Phase) Each fragment finds its MWOE Merge fragments adjacent to MWOE’s Until there is one fragment 36

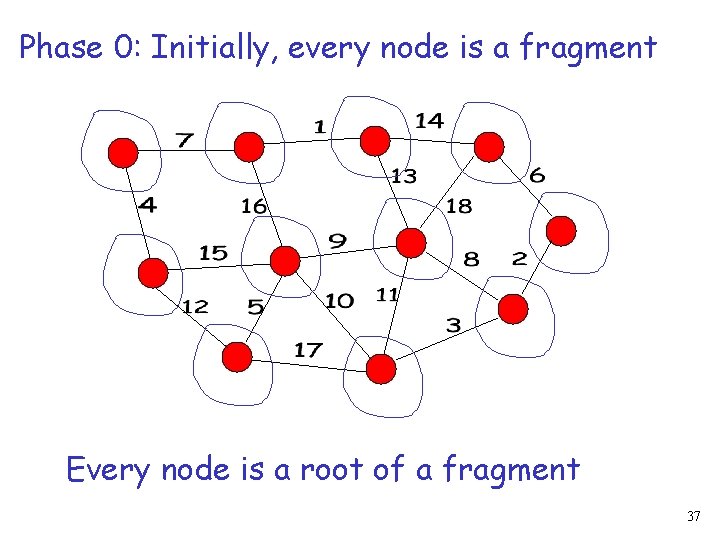
Phase 0: Initially, every node is a fragment Every node is a root of a fragment 37

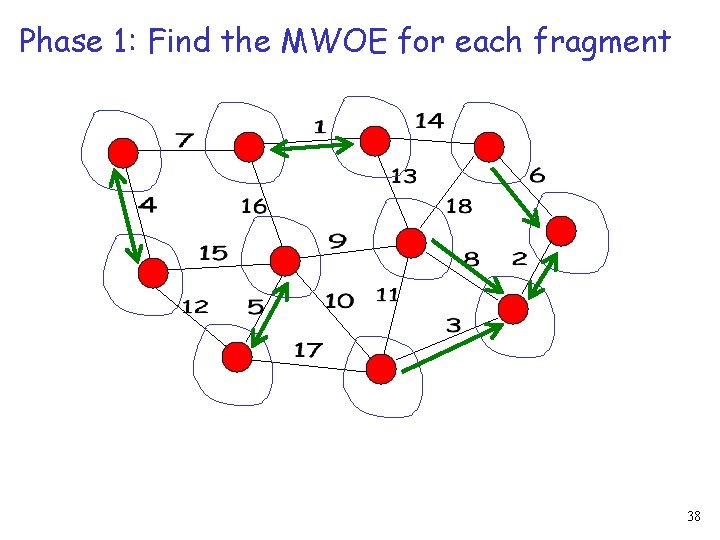
Phase 1: Find the MWOE for each fragment 38

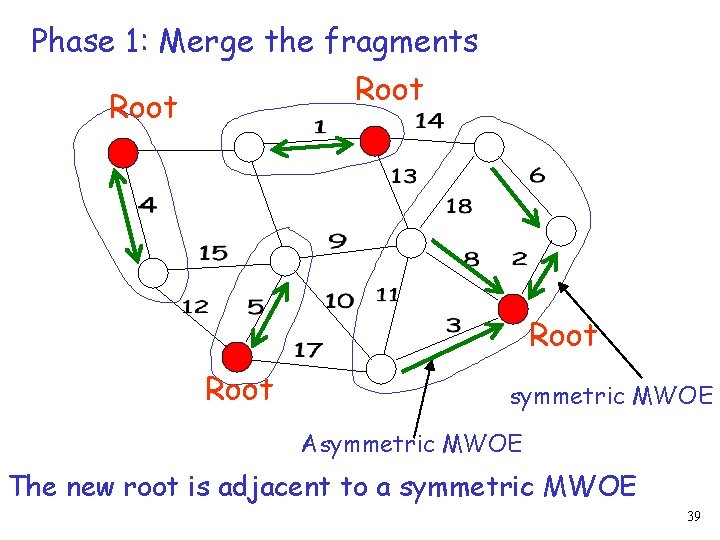
Phase 1: Merge the fragments Root symmetric MWOE Asymmetric MWOE The new root is adjacent to a symmetric MWOE 39

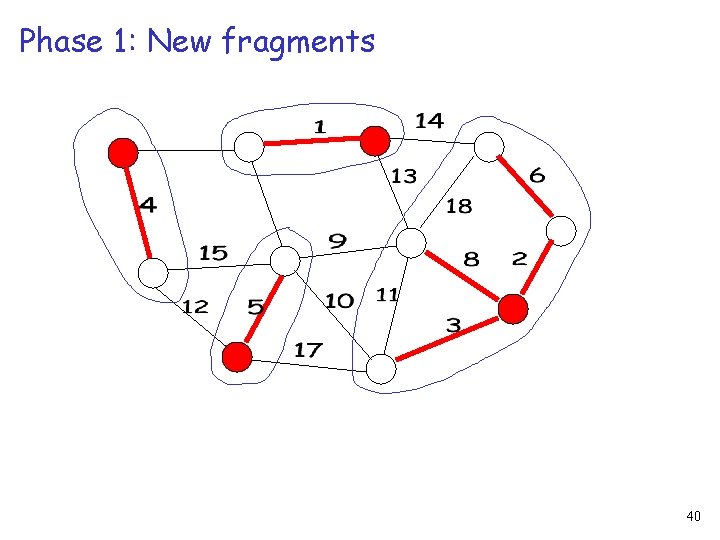
Phase 1: New fragments 40

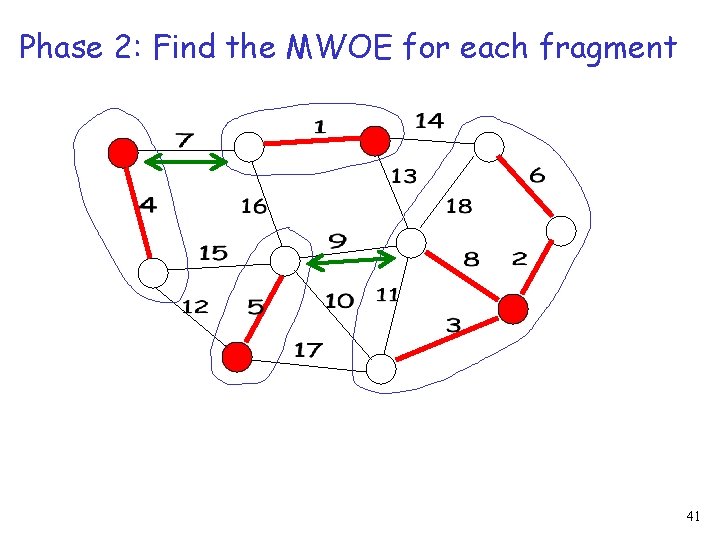
Phase 2: Find the MWOE for each fragment 41

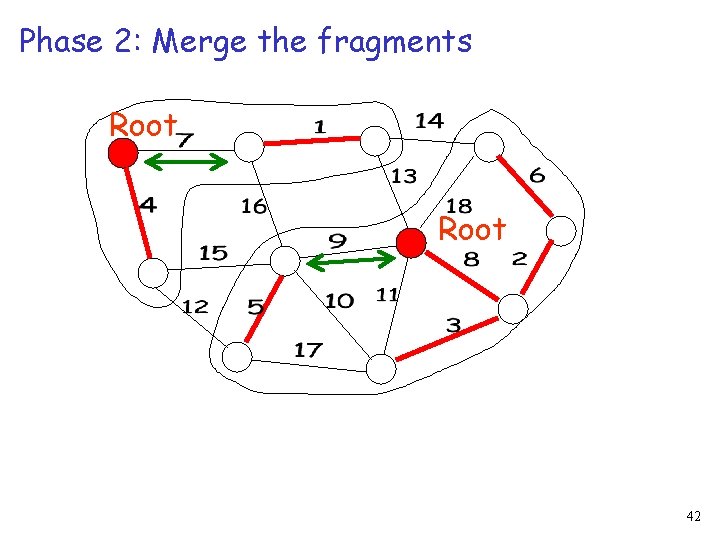
Phase 2: Merge the fragments Root 42

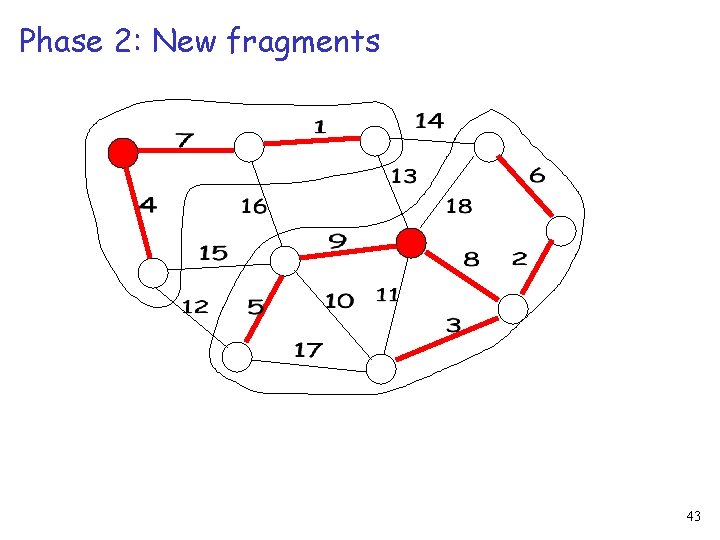
Phase 2: New fragments 43

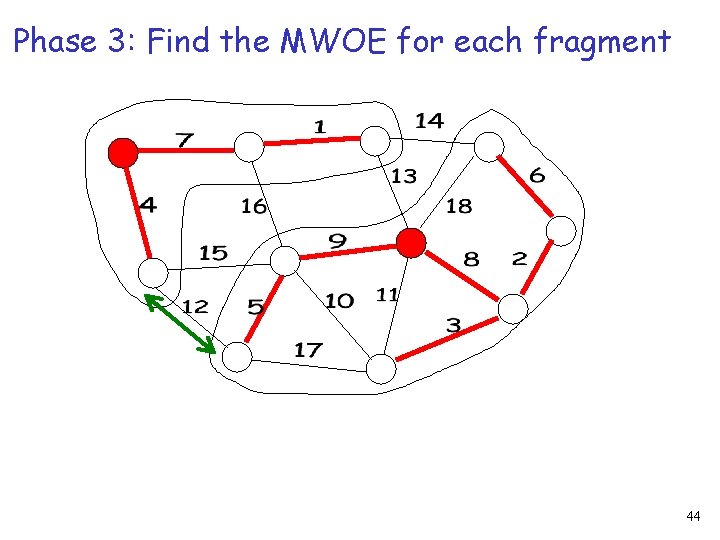
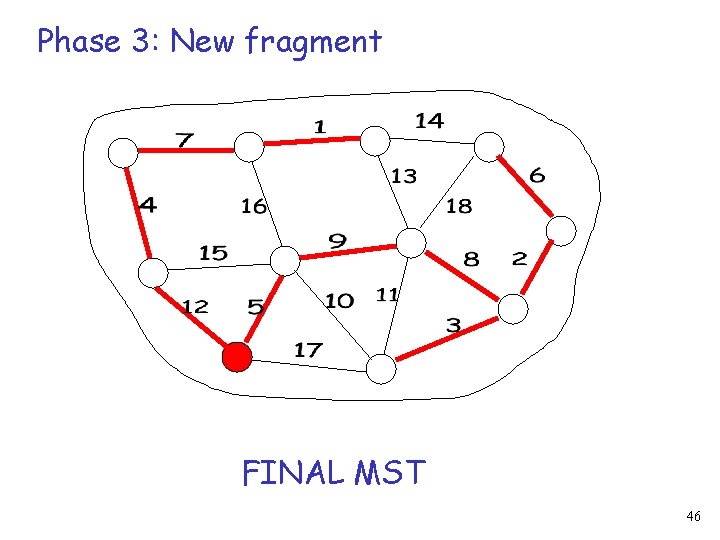
Phase 3: Find the MWOE for each fragment 44

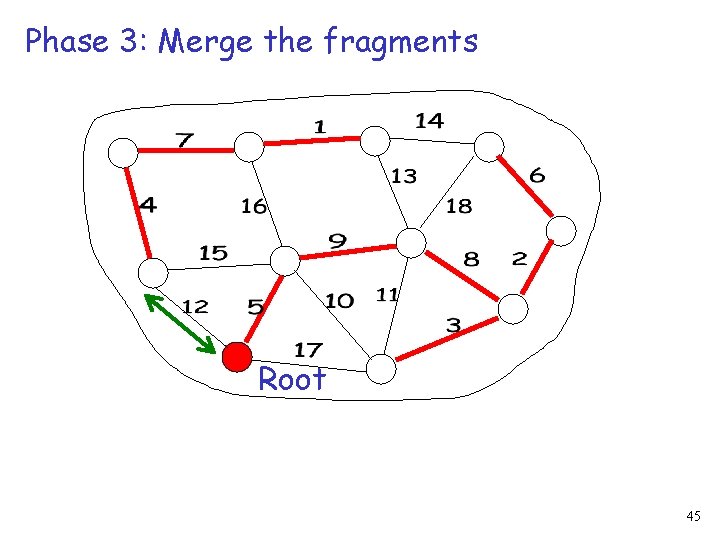
Phase 3: Merge the fragments Root 45

Phase 3: New fragment FINAL MST 46

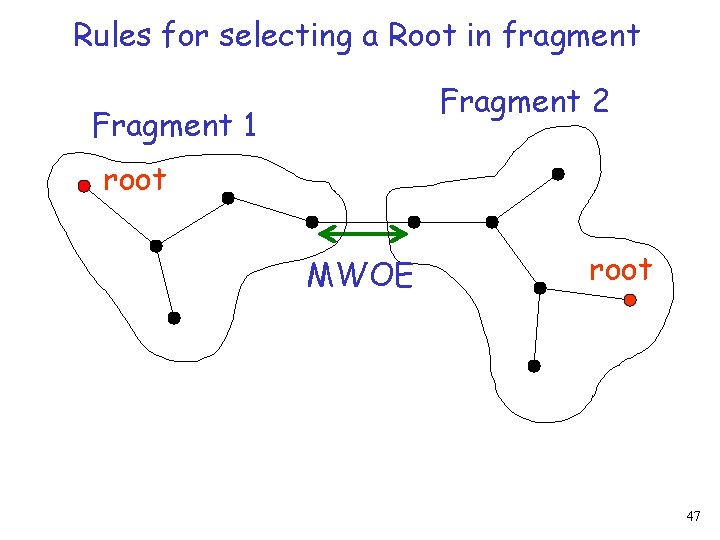
Rules for selecting a Root in fragment Fragment 2 Fragment 1 root MWOE root 47

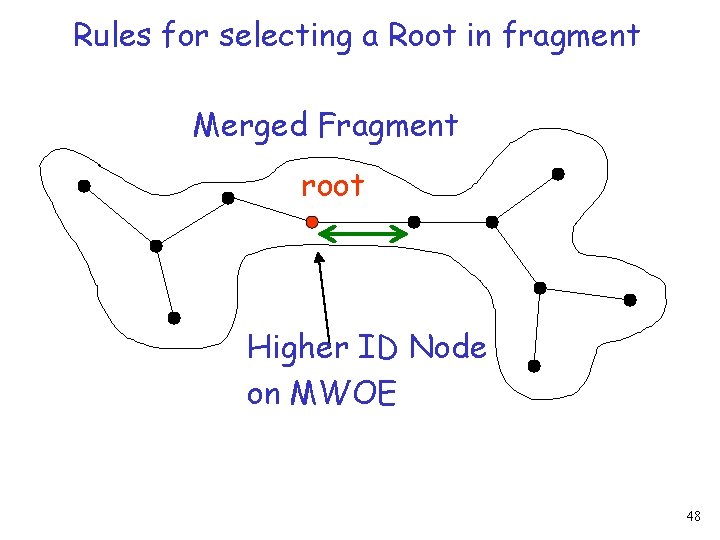
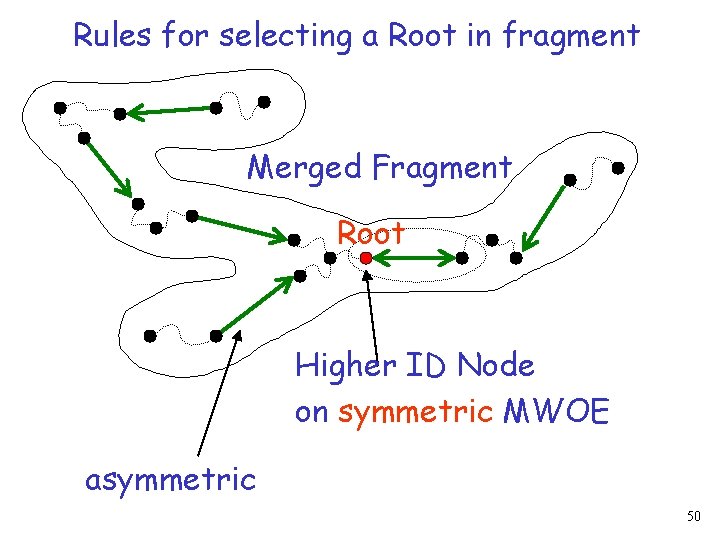
Rules for selecting a Root in fragment Merged Fragment root Higher ID Node on MWOE 48

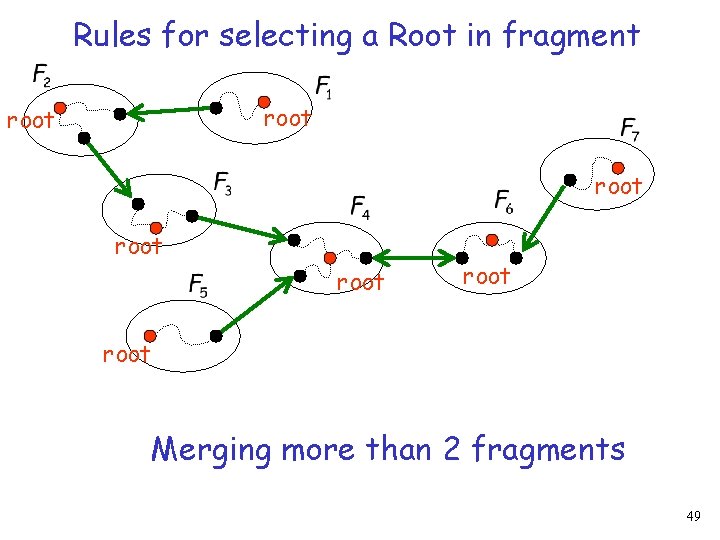
Rules for selecting a Root in fragment root root Merging more than 2 fragments 49

Rules for selecting a Root in fragment Merged Fragment Root Higher ID Node on symmetric MWOE asymmetric 50

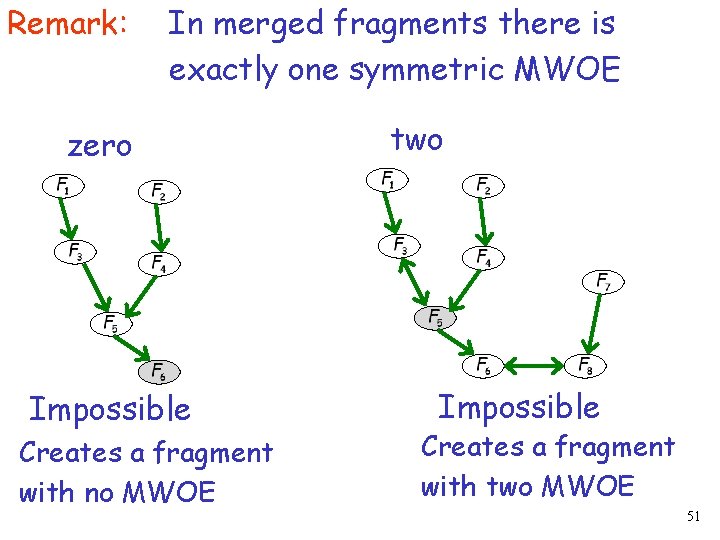
Remark: In merged fragments there is exactly one symmetric MWOE zero Impossible Creates a fragment with no MWOE two Impossible Creates a fragment with two MWOE 51

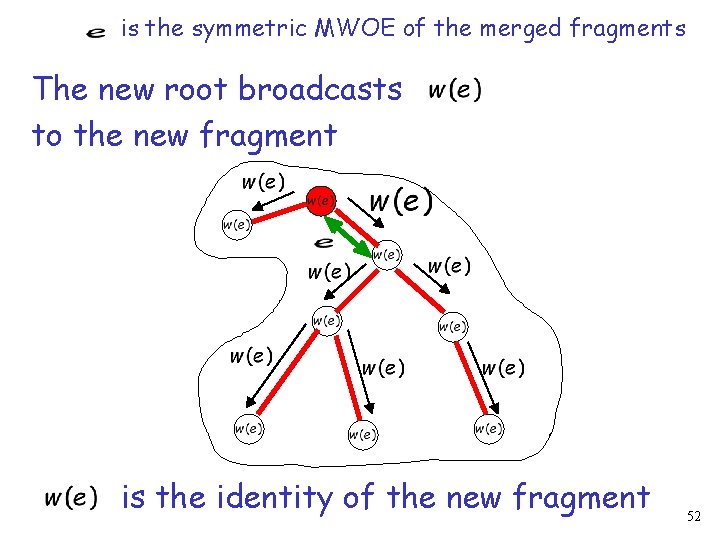
is the symmetric MWOE of the merged fragments The new root broadcasts to the new fragment is the identity of the new fragment 52

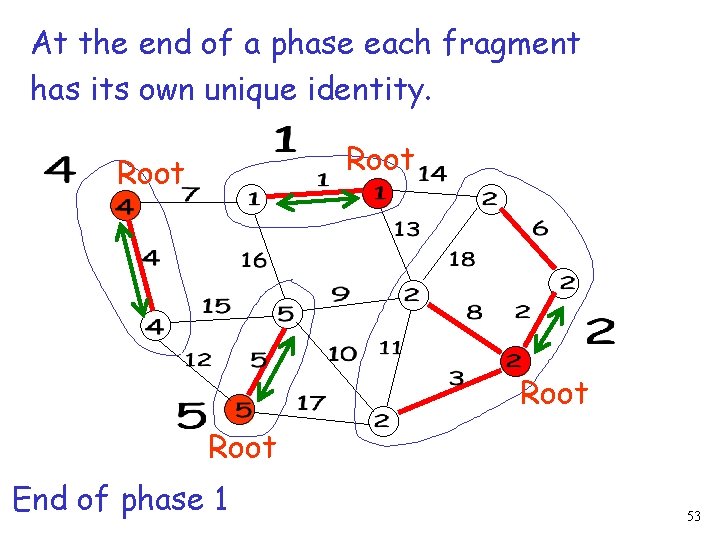
At the end of a phase each fragment has its own unique identity. Root End of phase 1 53

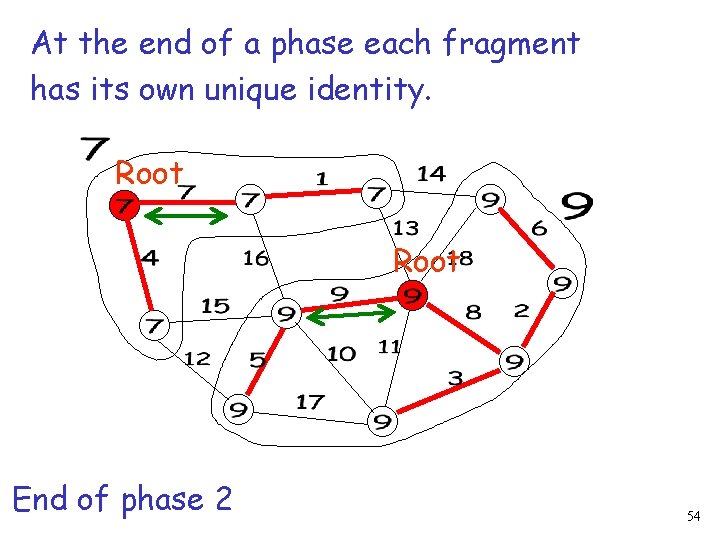
At the end of a phase each fragment has its own unique identity. Root End of phase 2 54

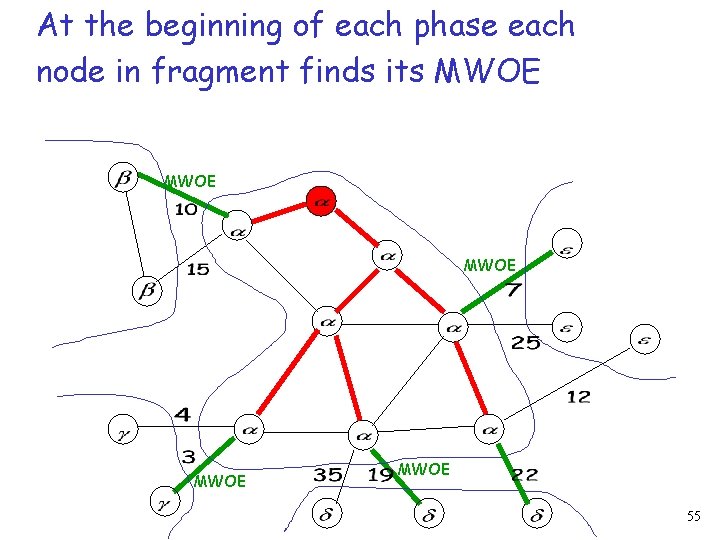
At the beginning of each phase each node in fragment finds its MWOE MWOE 55

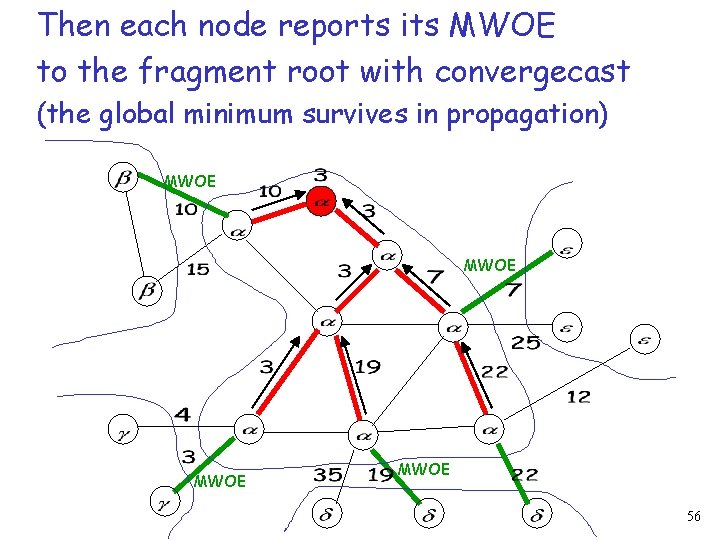
Then each node reports its MWOE to the fragment root with convergecast (the global minimum survives in propagation) MWOE 56

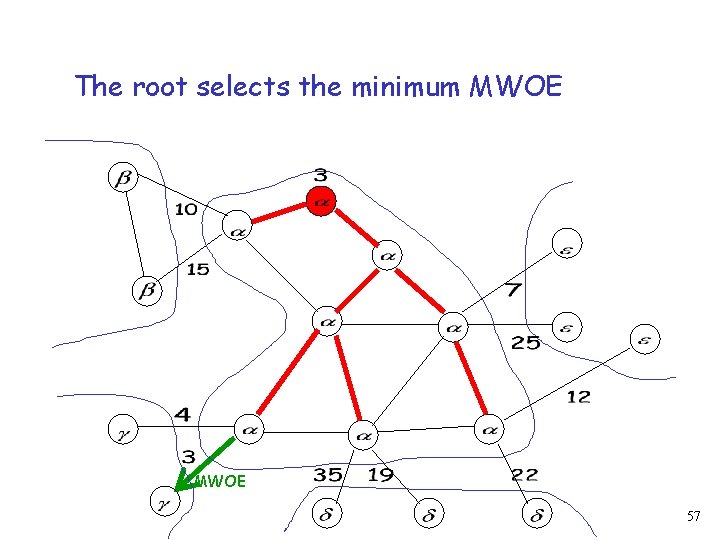
The root selects the minimum MWOE 57

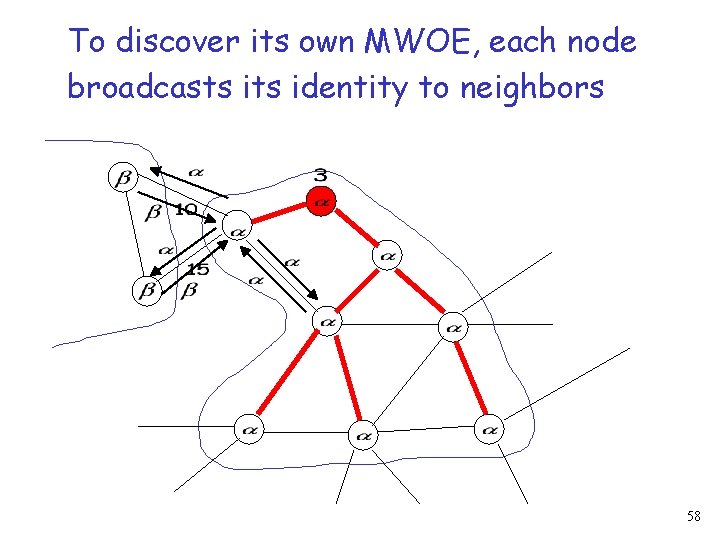
To discover its own MWOE, each node broadcasts identity to neighbors 58

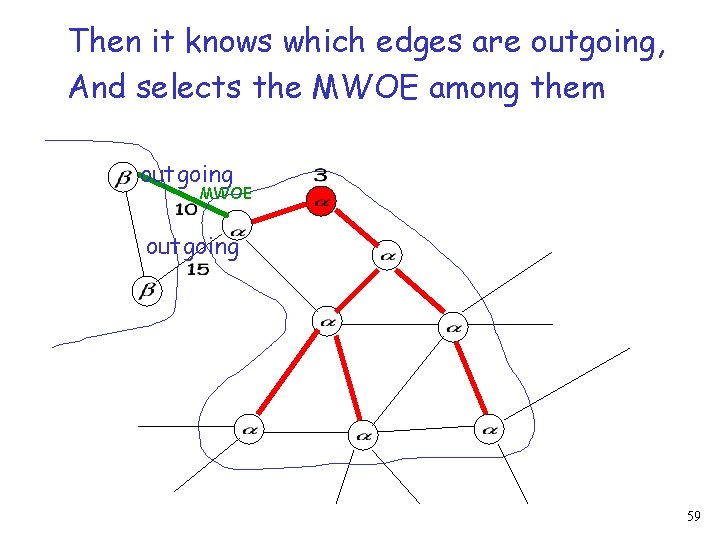
Then it knows which edges are outgoing, And selects the MWOE among them outgoing MWOE outgoing 59

Complexity Phase Smallest Fragment size (#nodes) 60

Maximum possible fragment size Number of nodes Maximum phase: 61

Time of a phase: Time to convergecast MWOE to root: (maximum fragment size is ) Time to connect new fragments: (Each fragment sends one message on its MWOE) Time of root to broadcast identity: Total phase time: 62

Algorithm Time Total time = Phase time X #phases = Lower bound: 63

Messages in a phase: Messages for nodes to find MWOE: (on each edge 2 messages) Messages to convergecast to root: (maximum fragment size is ) Messages to connect new fragments: (Each fragment sends one message on its MWOE) Messages to broadcast identity: Total phase messages: 64

Algorithm messages Total messages = Phase messages X #phases Can be improved to 65

Asynchronous Version of GHS Algorithm Simulates the synchronous version Every fragment has a level 66

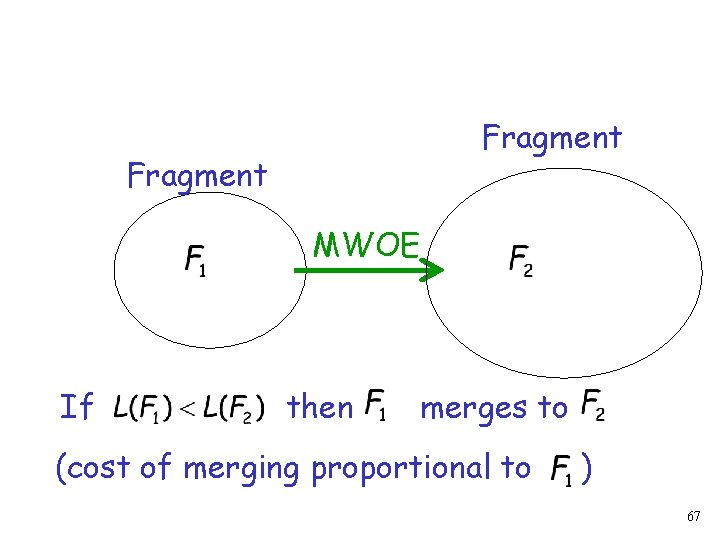
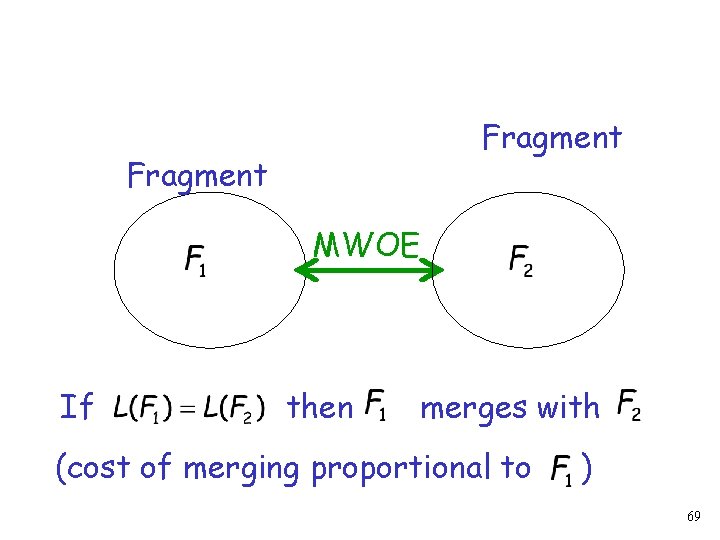
Fragment MWOE If then merges to (cost of merging proportional to ) 67

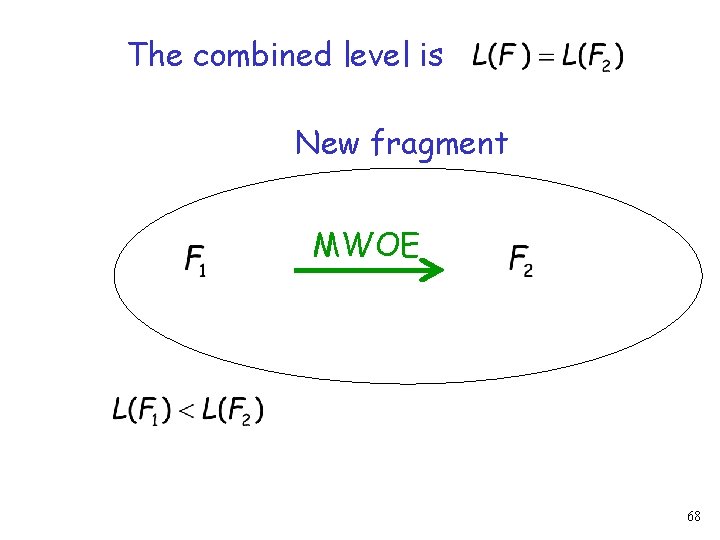
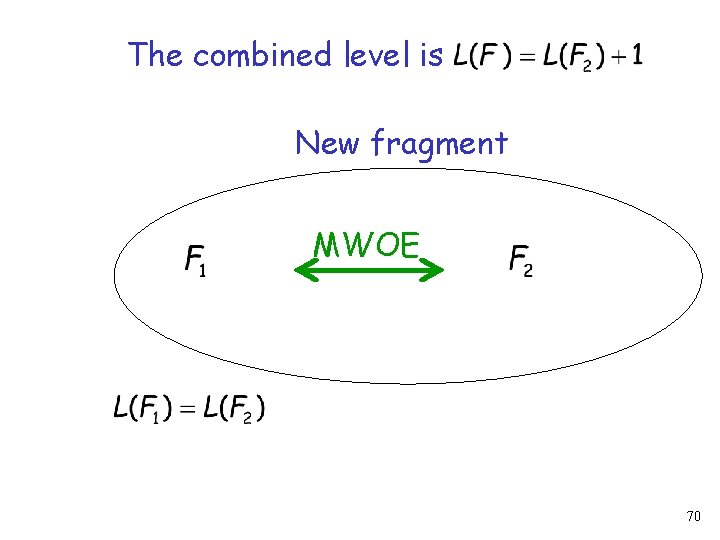
The combined level is New fragment MWOE 68

Fragment MWOE If then merges with (cost of merging proportional to ) 69

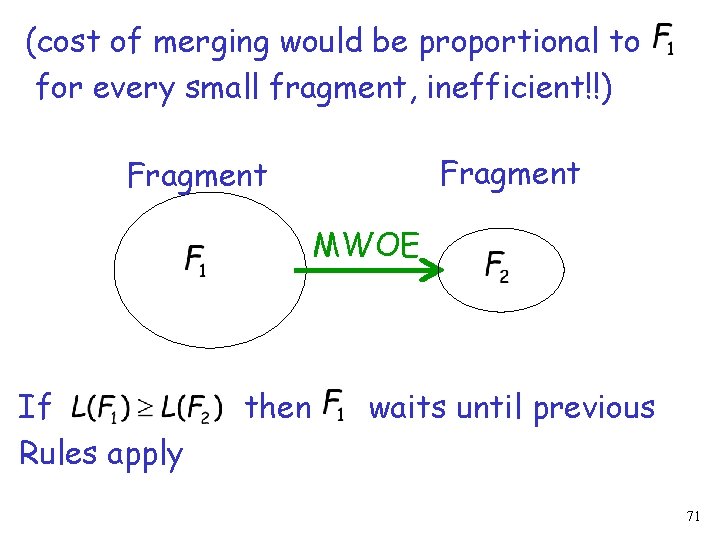
The combined level is New fragment MWOE 70

(cost of merging would be proportional to for every small fragment, inefficient!!) Fragment MWOE If Rules apply then waits until previous 71