Minimum Spanning Tree in expected linear time Epilogue



![Today’s Topic Expected O(m)-time comparisonbased algorithm for MST [Karger-Klein-Tarjan, JACM 1995] 7 Today’s Topic Expected O(m)-time comparisonbased algorithm for MST [Karger-Klein-Tarjan, JACM 1995] 7](https://slidetodoc.com/presentation_image/36757a4d64a0c4a46a7e1f529dc636a6/image-7.jpg)








![Tool 1: Dixon-Rauch-Tarjan • [SIAM J. Computing 1992] – Given a spanning tree T Tool 1: Dixon-Rauch-Tarjan • [SIAM J. Computing 1992] – Given a spanning tree T](https://slidetodoc.com/presentation_image/36757a4d64a0c4a46a7e1f529dc636a6/image-21.jpg)













- Slides: 34

• Minimum Spanning Tree in expected linear time. • Epilogue: Top-in card shuffling. 1

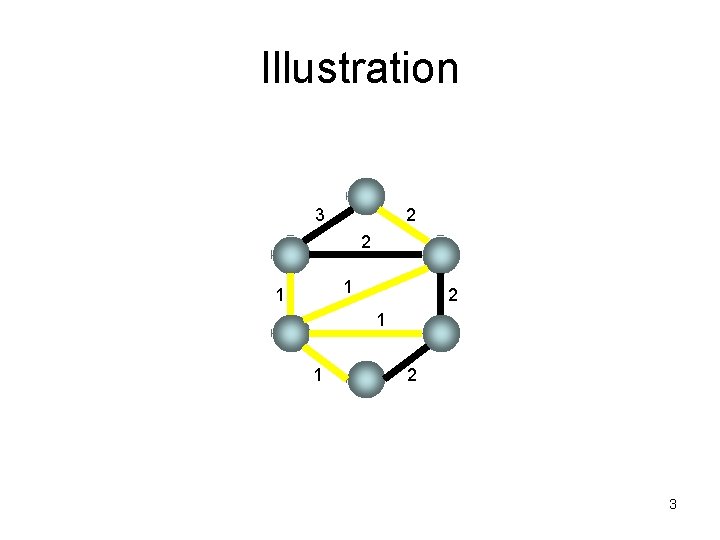
The problem • Input: – A connected n-node m -edge graph G with edge weight w. • Output: – A spanning tree T of G with minimum w(T). 2

Illustration 3 2 2 1 1 2 3

Inventor of MST • Otakar Borůvka – Czech scientist – Introduced the problem – Gave an O(m log n) time algorithm – The original paper was written in Czech in 1926. – The purpose was to efficiently provide electric coverage of Bohemia. 4

Bohemia – Western Czech 5

The competition • Unit-cost RAM model – O(m) Fredman-Willard (FOCS 1990) • Deterministic comparison based algorithms. – – – O(m log n) Borůvka, Prim, Dijkstra, Kruskal, … O(m log n) Yao (1975), Cheriton-Tarjan (1976) O(m (m, n)) Fredman-Tarjan (1987) O(m log (m, n)) Gabow-Galil-Spencer-Tarjan (1986) O(m (m, n)) Chazelle (JACM 2000) O(m) Holy grail 6
![Todays Topic Expected Omtime comparisonbased algorithm for MST KargerKleinTarjan JACM 1995 7 Today’s Topic Expected O(m)-time comparisonbased algorithm for MST [Karger-Klein-Tarjan, JACM 1995] 7](https://slidetodoc.com/presentation_image/36757a4d64a0c4a46a7e1f529dc636a6/image-7.jpg)
Today’s Topic Expected O(m)-time comparisonbased algorithm for MST [Karger-Klein-Tarjan, JACM 1995] 7

Without loss of generality • We may assume that all edge weights are distinct. • Why? 8

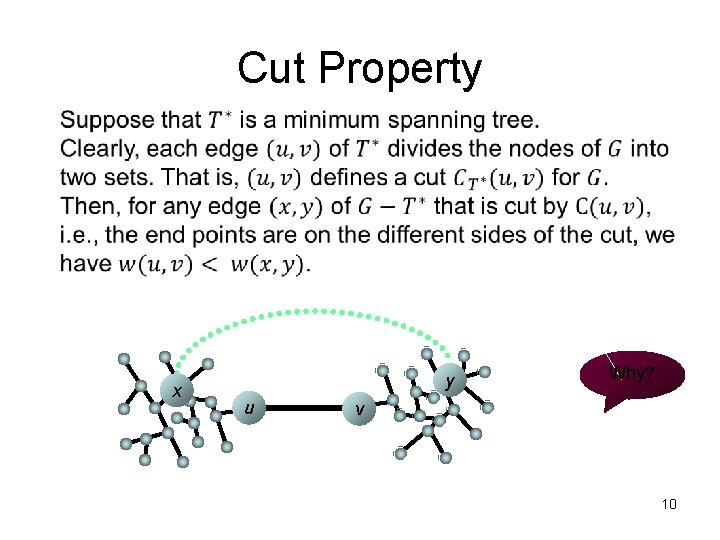
Warm-up: Fundamental Properties of MST (a) Cut Property (b) Cycle Property (c) Uniqueness Property 9

Cut Property x y u Why? v 10

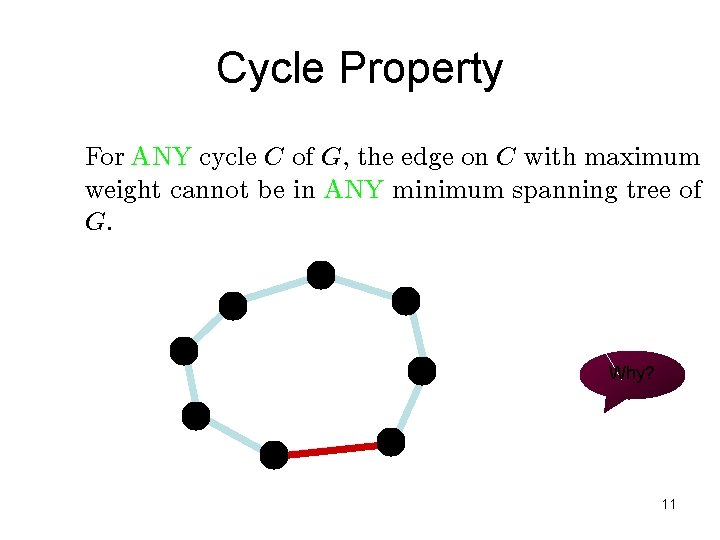
Cycle Property For ANY cycle C of G, the edge on C with maximum weight cannot be in ANY minimum spanning tree of G. Why? 11

Uniqueness Property u v T T ¤ x y 12

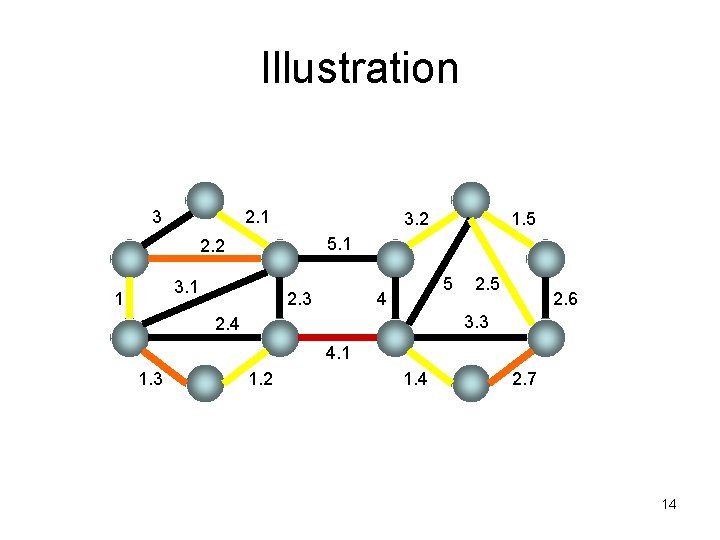
Boruvka’s algorithm • Repeat the following procedure until the resulting graph becomes a single node. – For each node u, mark its lightest incident edge. – Now, the marked edges form a forest F. Add the edges of F into the set of edges to be reported. – Contract each maximal subtree of F into a single node. 13

Illustration 3 2. 1 3. 2 5. 1 2. 2 3. 1 1 1. 5 5 4 2. 3 2. 5 2. 6 3. 3 2. 4 4. 1 1. 3 1. 2 1. 4 2. 7 14

Running time = O(m log n) 15

Karger-Klein-Tarjan 16

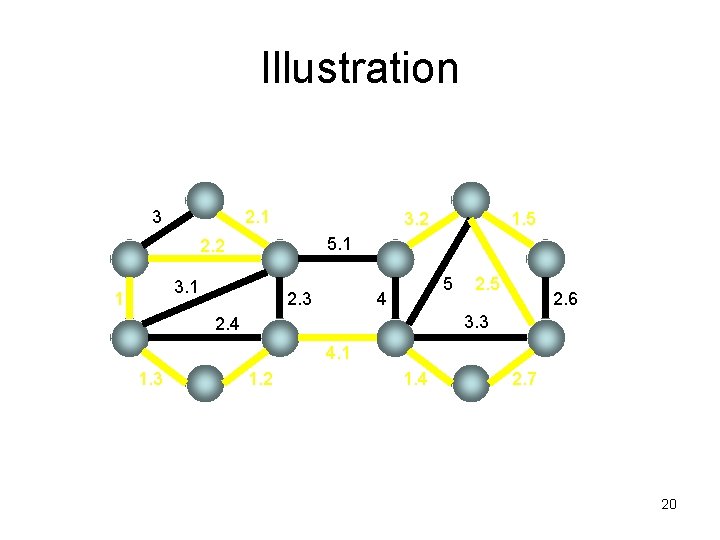
Resorting to the cycle property! Question: What edges can be deleted without affecting the optimality of the output tree? 17

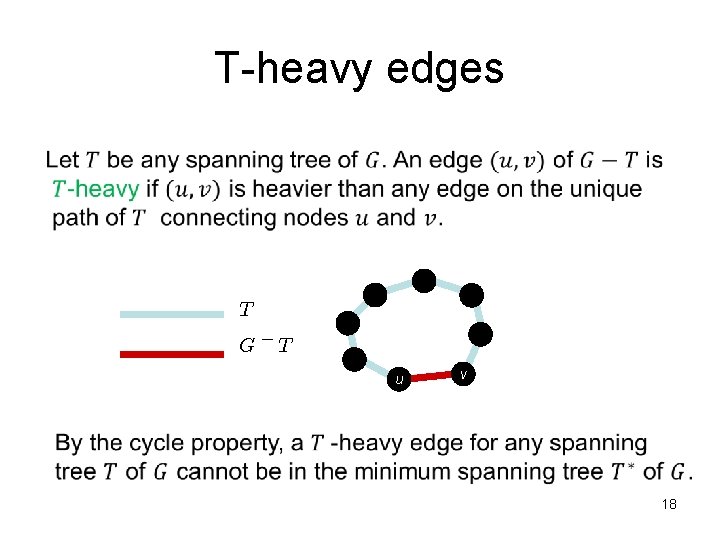
T-heavy edges T G¡T u v 18

The Heaviness Lemma 19

Illustration 3 2. 1 3. 2 5. 1 2. 2 3. 1 1 1. 5 2. 3 5 4 2. 5 2. 6 3. 3 2. 4 4. 1 1. 3 1. 2 1. 4 2. 7 20
![Tool 1 DixonRauchTarjan SIAM J Computing 1992 Given a spanning tree T Tool 1: Dixon-Rauch-Tarjan • [SIAM J. Computing 1992] – Given a spanning tree T](https://slidetodoc.com/presentation_image/36757a4d64a0c4a46a7e1f529dc636a6/image-21.jpg)
Tool 1: Dixon-Rauch-Tarjan • [SIAM J. Computing 1992] – Given a spanning tree T of G, it takes (deterministic) O(m) time to output all T-heavy edges of G. 21

Verifying MST is easier! • It follows from Dixon-Rauch-Tarjan that verifying whether an input tree T is the minimum spanning tree G can be done in (deterministic) O(m) time. 22

Tool 2: A Sampling Lemma 23

The (recursive) algorithm 24

Expected Running Time 25

Comments • The original sampling lemma, which is slightly more complicated, is due to Karger, Klein, and Tarjan. • The version we see is due to Timothy Chan [IPL 1998]. – The statement and its proof are both extremely simple! 26

Chan’s Proof 27

28

29

Shuffling cards 30

Top-In Shuffling • Suppose that we are given a deck of n cards. • Each iteration, we pick the card on top, and then insert it back to the deck at a random position: there are n positions, each with probability 1/n. 31

Question How many iterations are required to make the deck random? 32

33

34