Minimum Spanning Tree By Prof Uzair Salman Spanning

Minimum Spanning Tree By: Prof. Uzair Salman

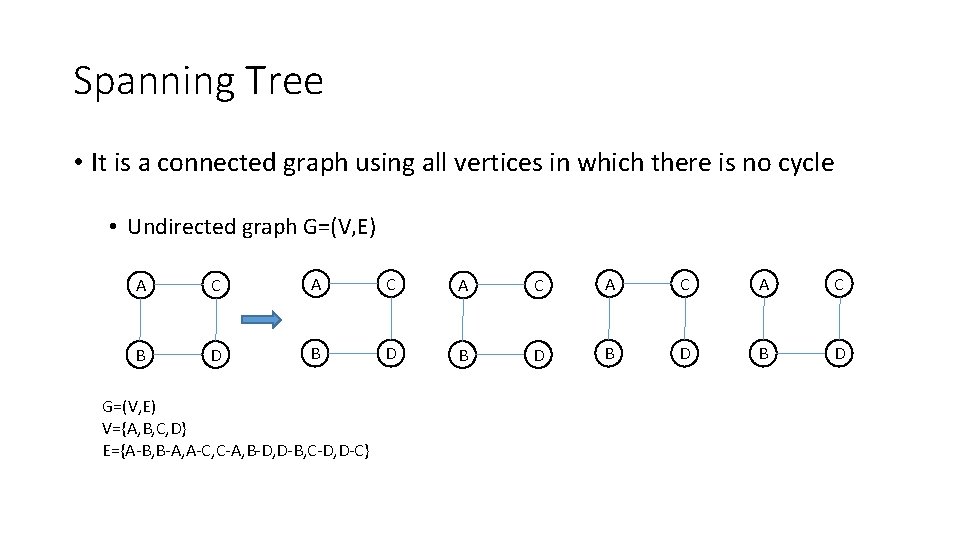
Spanning Tree • It is a connected graph using all vertices in which there is no cycle • Undirected graph G=(V, E) A C A C A C B D B D B D G=(V, E) V={A, B, C, D} E={A-B, B-A, A-C, C-A, B-D, D-B, C-D, D-C}

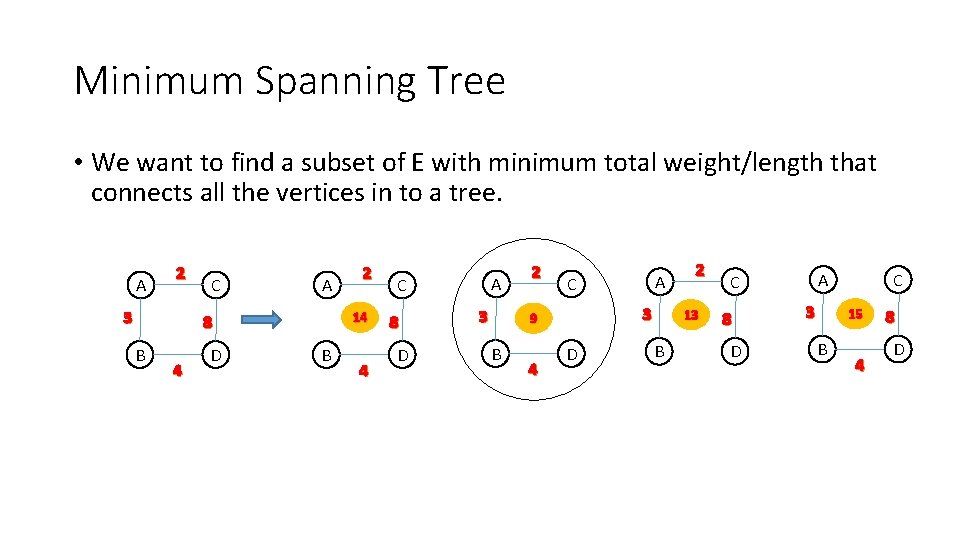
Minimum Spanning Tree • We want to find a subset of E with minimum total weight/length that connects all the vertices in to a tree. A 2 3 C A 14 8 B 4 D 2 B 4 A C 8 D 3 2 C 3 9 B 4 A D 2 13 B A C 8 D 3 C 15 B 4 8 D

Applications of MST • Network design. • • • telephone Electrical Hydraulic TV cable Computer network road • Cluster analysis • Handwriting Recognition

Applications Contd. . • The phone company task is to provide phone lines to a village with 10 houses, each labeled H 1 through H 10. • A single cable must connects each home. The cable must run through houses H 1, H 2, and so forth, up through H 10. • Each node is a house, and the edges are the means by which one house can be wired up to another. • The weights of the edges dictate the distance between the homes. • Their task is to wire up all ten houses using the least amount of telephone wiring possible.

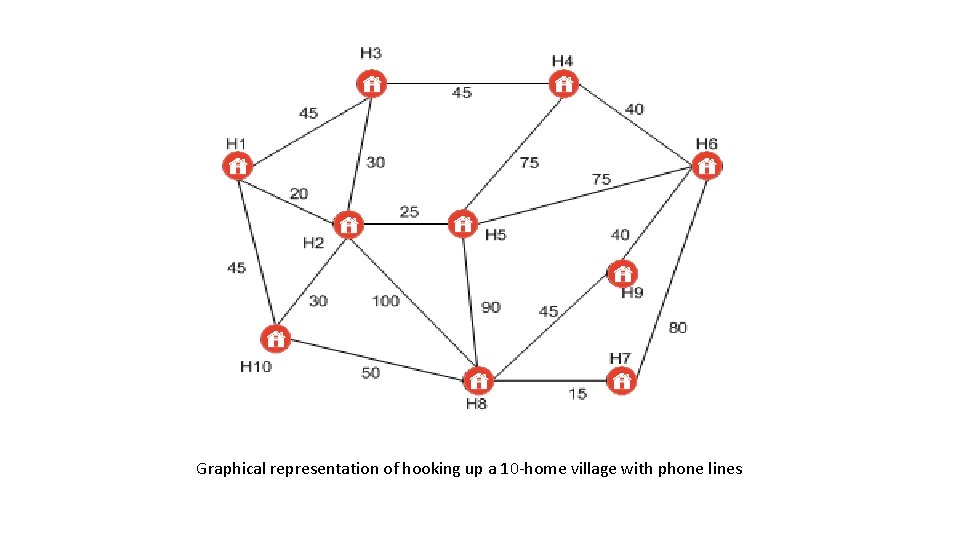
Graphical representation of hooking up a 10 -home village with phone lines

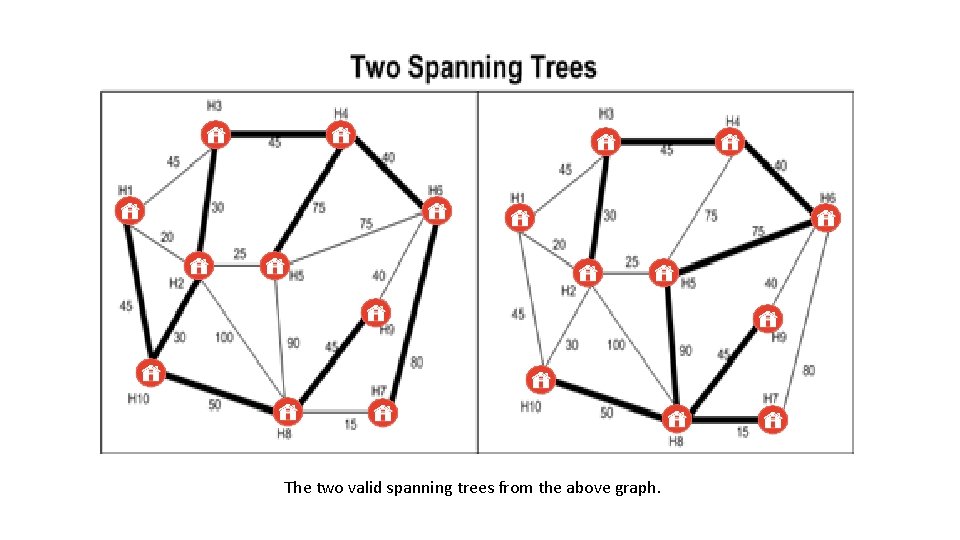
The two valid spanning trees from the above graph.

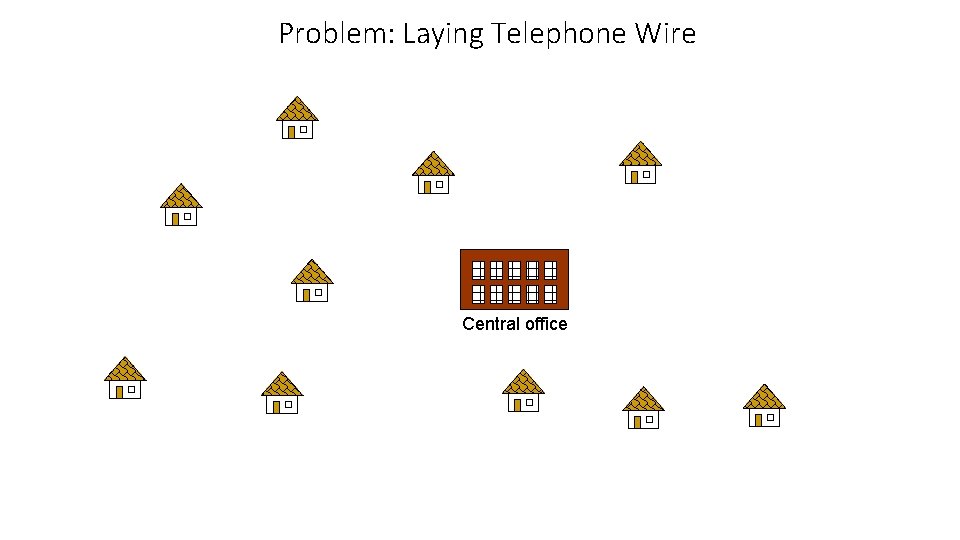
Problem: Laying Telephone Wire Central office

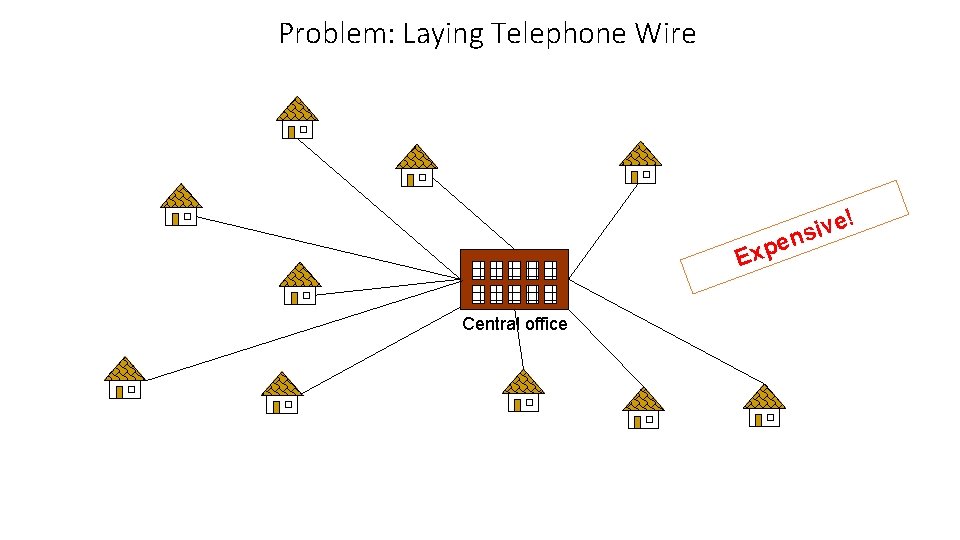
Problem: Laying Telephone Wire ! e v i s n e xp E Central office

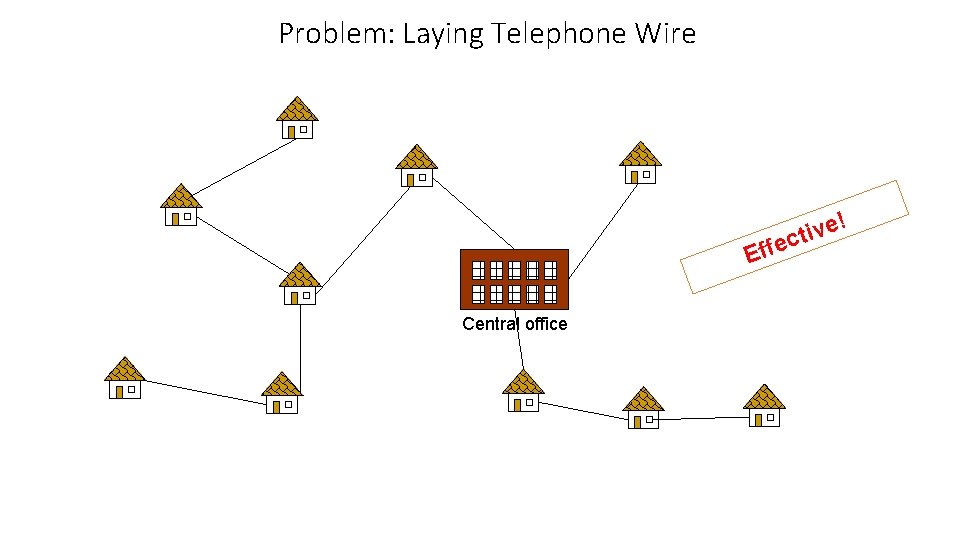
Problem: Laying Telephone Wire e! v i t ec Eff Central office

Algorithm for Minimum Spanning Tree (MST) • Two basic algorithms exists • Kruskal’s • Prim • May have different complexity (efficiency) depending on the topology of the network.

MST Kruskal’s Algorithm 1. Sort all the edges in non-decreasing order of their weight. 2. Pick the smallest edge. Check if it forms a cycle with the spanning tree formed so far. If cycle is not formed, include this edge. Else, discard it. 3. Repeat step#2 until there are (V-1) edges in the spanning tree.

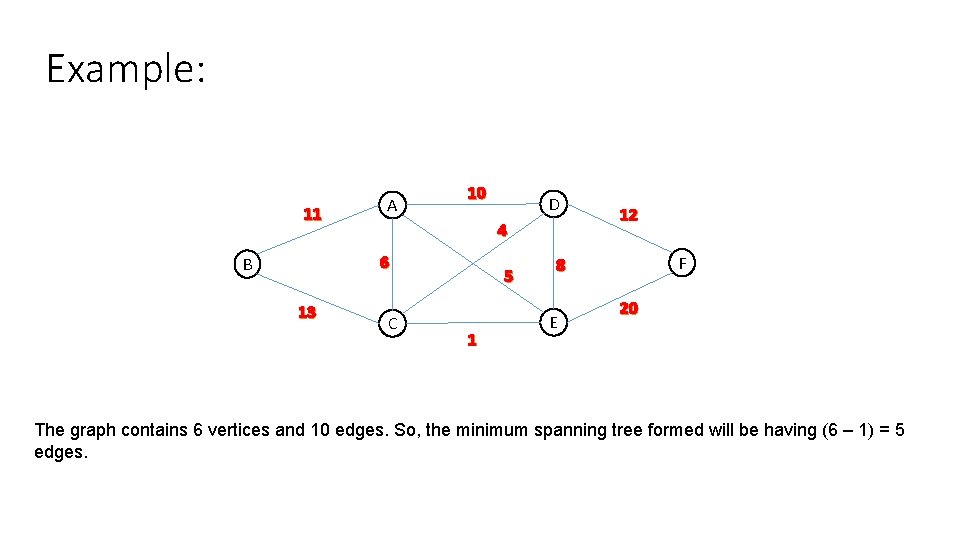
Example: 11 A 10 4 6 B 13 D C 5 1 12 F 8 E 20 The graph contains 6 vertices and 10 edges. So, the minimum spanning tree formed will be having (6 – 1) = 5 edges.

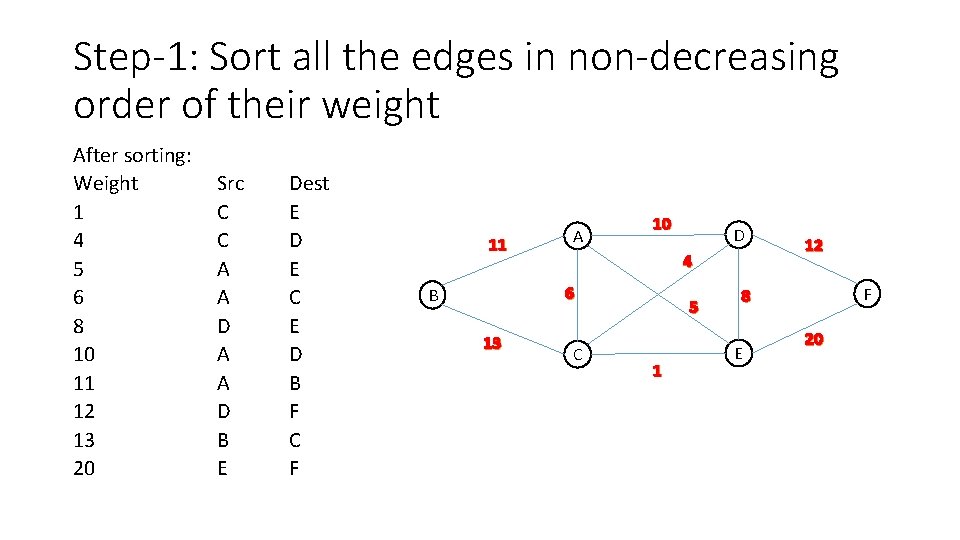
Step-1: Sort all the edges in non-decreasing order of their weight After sorting: Weight 1 4 5 6 8 10 11 12 13 20 Src C C A A D B E Dest E D E C E D B F C F 11 A 10 4 6 B 13 D C 5 1 12 F 8 E 20

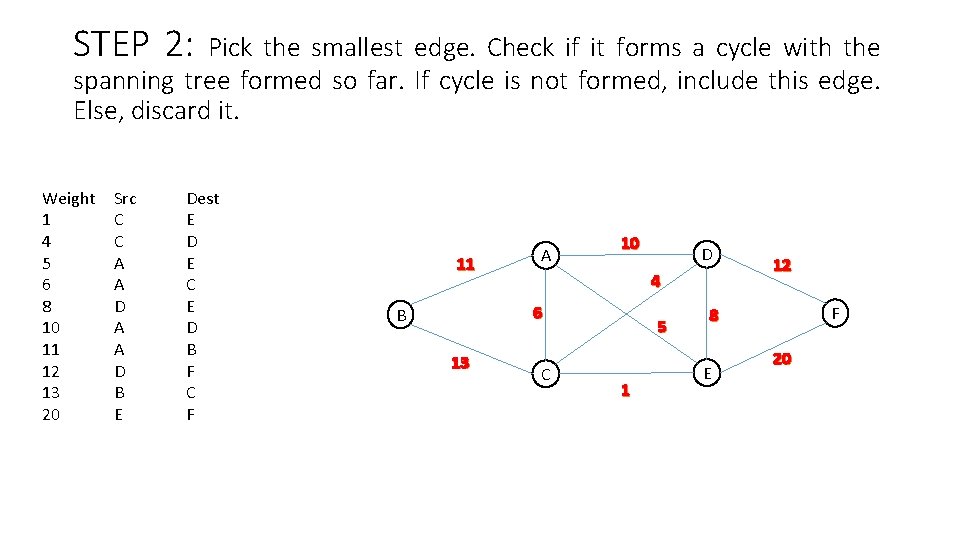
STEP 2: Pick the smallest edge. Check if it forms a cycle with the spanning tree formed so far. If cycle is not formed, include this edge. Else, discard it. Weight 1 4 5 6 8 10 11 12 13 20 Src C C A A D B E Dest E D E C E D B F C F 11 A 10 4 6 B 13 D C 5 1 12 F 8 E 20

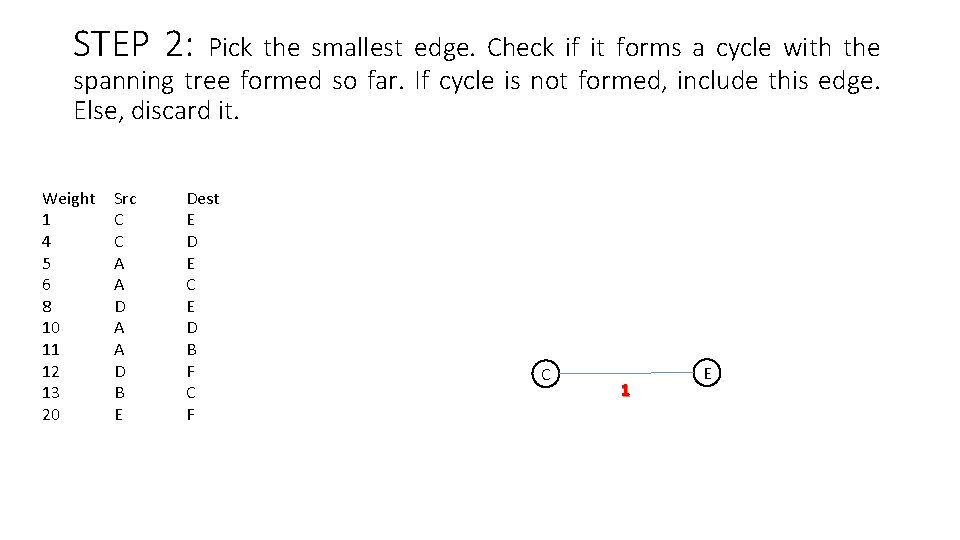
STEP 2: Pick the smallest edge. Check if it forms a cycle with the spanning tree formed so far. If cycle is not formed, include this edge. Else, discard it. Weight 1 4 5 6 8 10 11 12 13 20 Src C C A A D B E Dest E D E C E D B F C 1 E

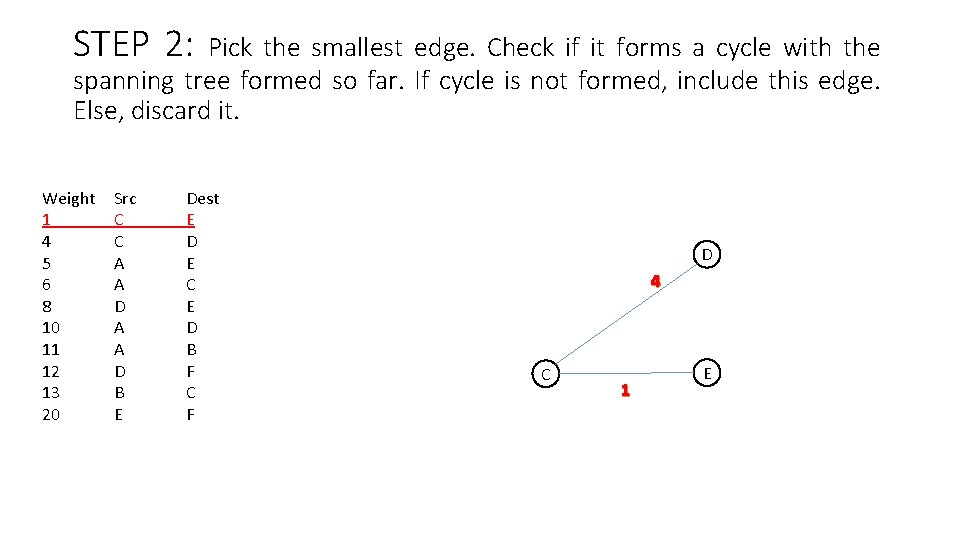
STEP 2: Pick the smallest edge. Check if it forms a cycle with the spanning tree formed so far. If cycle is not formed, include this edge. Else, discard it. Weight 1 4 5 6 8 10 11 12 13 20 Src C C A A D B E Dest E D E C E D B F C F D 4 C 1 E

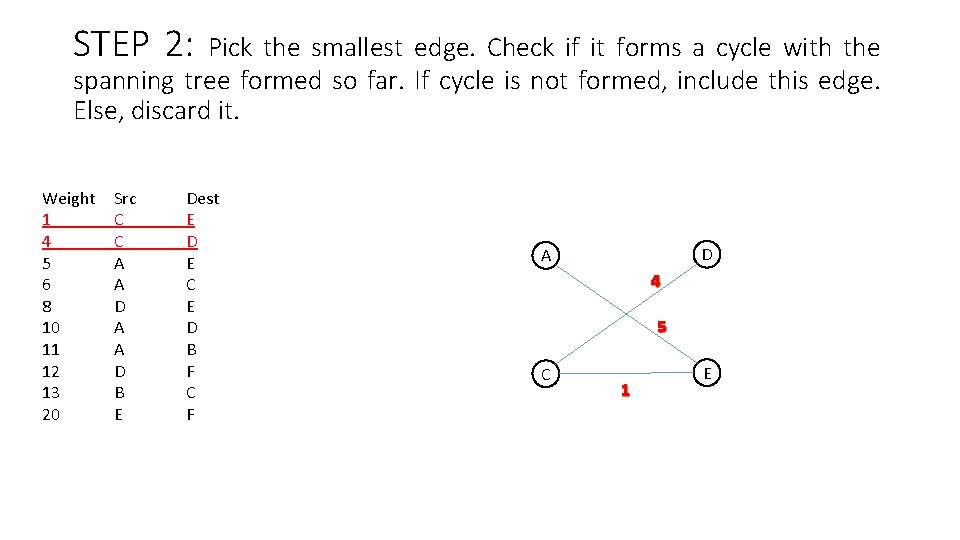
STEP 2: Pick the smallest edge. Check if it forms a cycle with the spanning tree formed so far. If cycle is not formed, include this edge. Else, discard it. Weight 1 4 5 6 8 10 11 12 13 20 Src C C A A D B E Dest E D E C E D B F C F D A 4 5 C 1 E

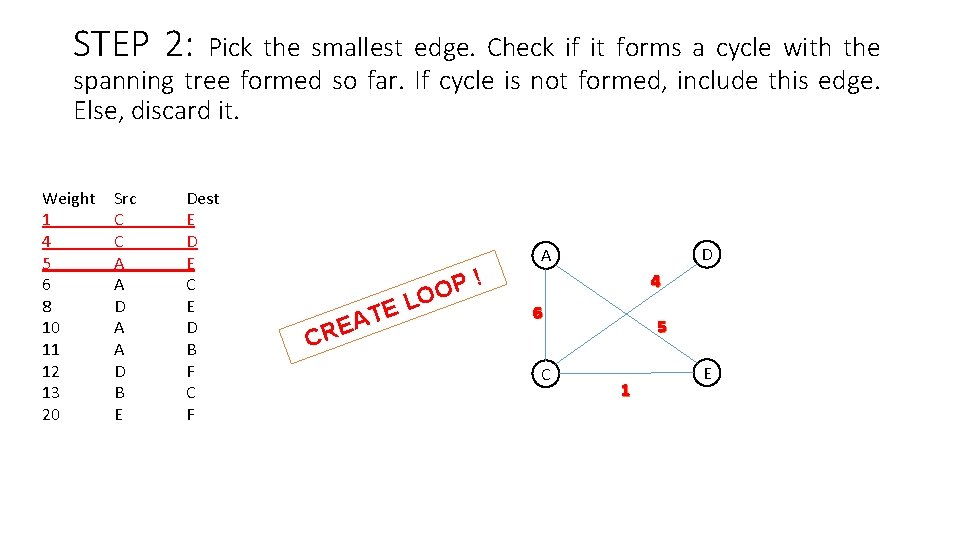
STEP 2: Pick the smallest edge. Check if it forms a cycle with the spanning tree formed so far. If cycle is not formed, include this edge. Else, discard it. Weight 1 4 5 6 8 10 11 12 13 20 Src C C A A D B E Dest E D E C E D B F C F E T A RE P O O L ! D A 4 6 5 C C 1 E

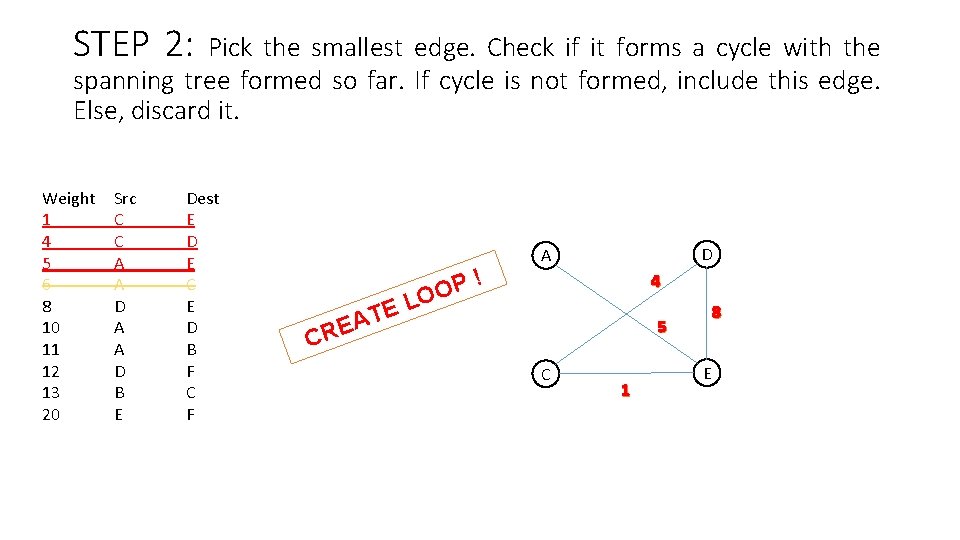
STEP 2: Pick the smallest edge. Check if it forms a cycle with the spanning tree formed so far. If cycle is not formed, include this edge. Else, discard it. Weight 1 4 5 6 8 10 11 12 13 20 Src C C A A D B E Dest E D E C E D B F C F E T A RE P O O L ! D A 4 8 5 C C 1 E

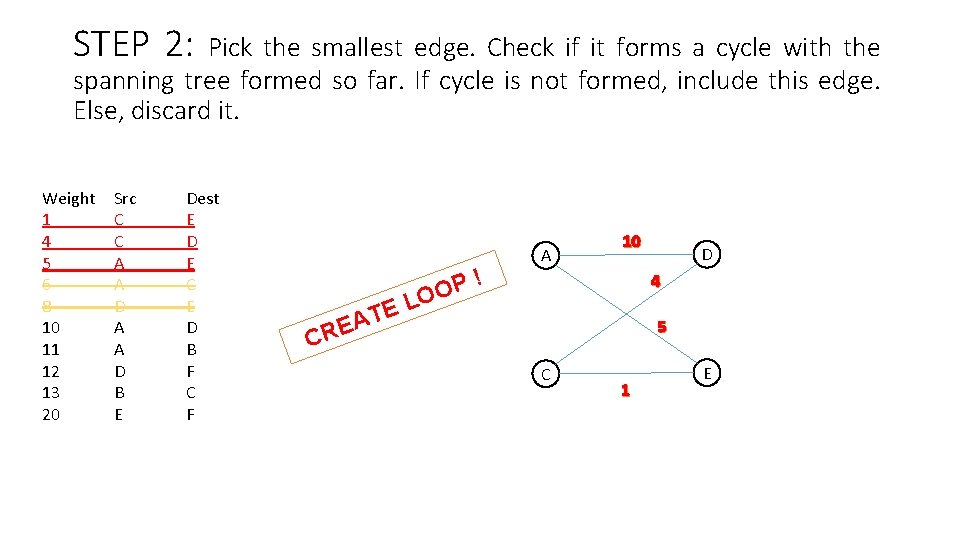
STEP 2: Pick the smallest edge. Check if it forms a cycle with the spanning tree formed so far. If cycle is not formed, include this edge. Else, discard it. Weight 1 4 5 6 8 10 11 12 13 20 Src C C A A D B E Dest E D E C E D B F C F E T A RE P O O L ! A 10 D 4 5 C C 1 E

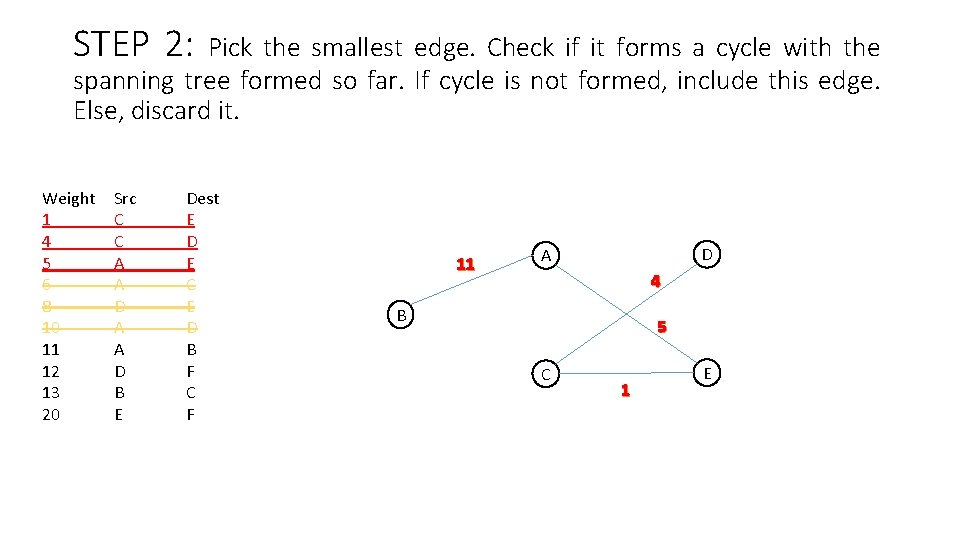
STEP 2: Pick the smallest edge. Check if it forms a cycle with the spanning tree formed so far. If cycle is not formed, include this edge. Else, discard it. Weight 1 4 5 6 8 10 11 12 13 20 Src C C A A D B E Dest E D E C E D B F C F 11 D A 4 B 5 C 1 E

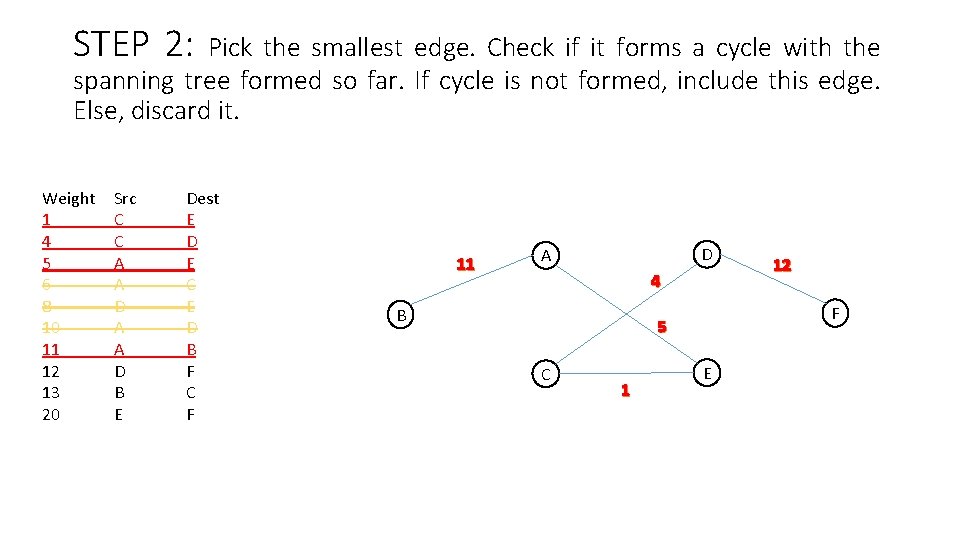
STEP 2: Pick the smallest edge. Check if it forms a cycle with the spanning tree formed so far. If cycle is not formed, include this edge. Else, discard it. Weight 1 4 5 6 8 10 11 12 13 20 Src C C A A D B E Dest E D E C E D B F C F 11 D A 4 B F 5 C 1 12 E

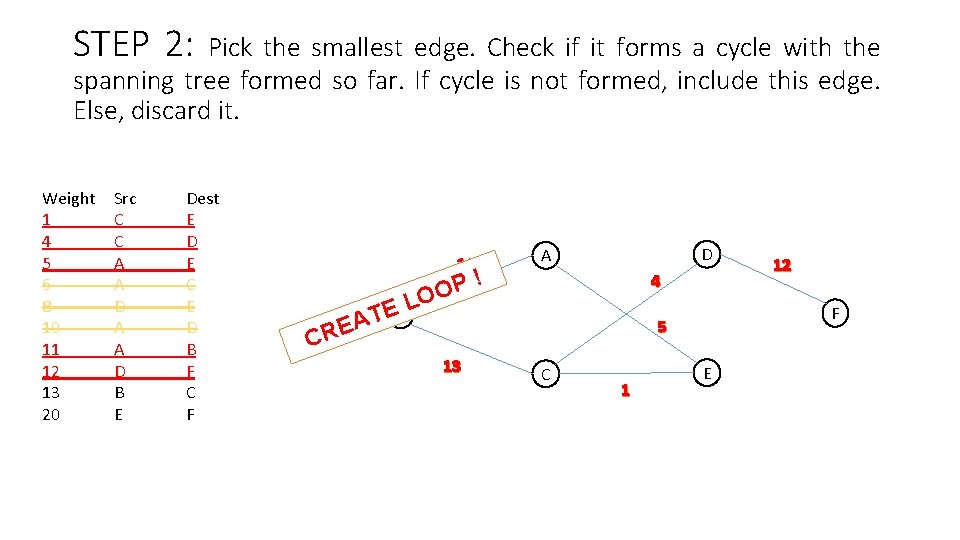
STEP 2: Pick the smallest edge. Check if it forms a cycle with the spanning tree formed so far. If cycle is not formed, include this edge. Else, discard it. Weight 1 4 5 6 8 10 11 12 13 20 Src C C A A D B E Dest E D E C E D B F C F 11 EB T A RE P O O L ! D A 4 13 F 5 C C 1 12 E

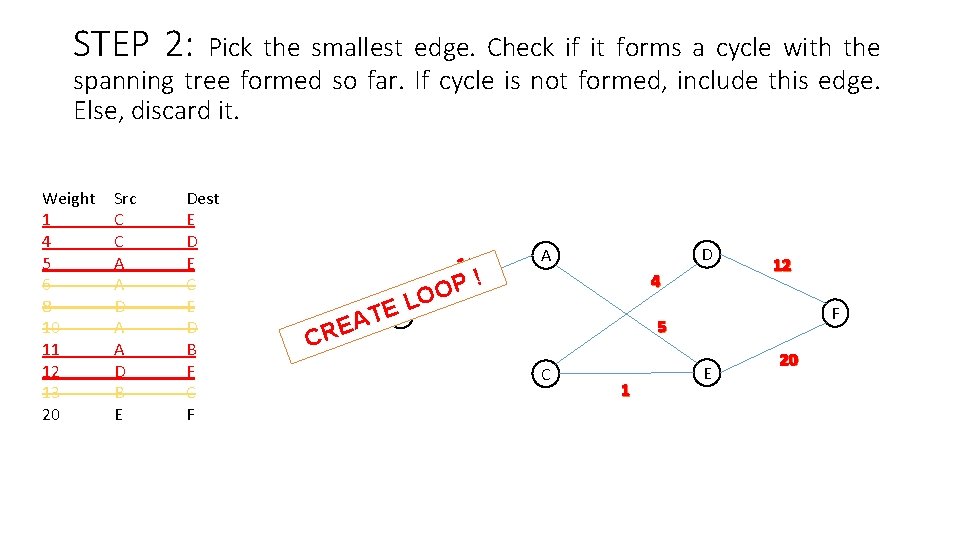
STEP 2: Pick the smallest edge. Check if it forms a cycle with the spanning tree formed so far. If cycle is not formed, include this edge. Else, discard it. Weight 1 4 5 6 8 10 11 12 13 20 Src C C A A D B E Dest E D E C E D B F C F 11 EB T A RE P O O L ! D A 4 12 F 5 C C 1 E 20

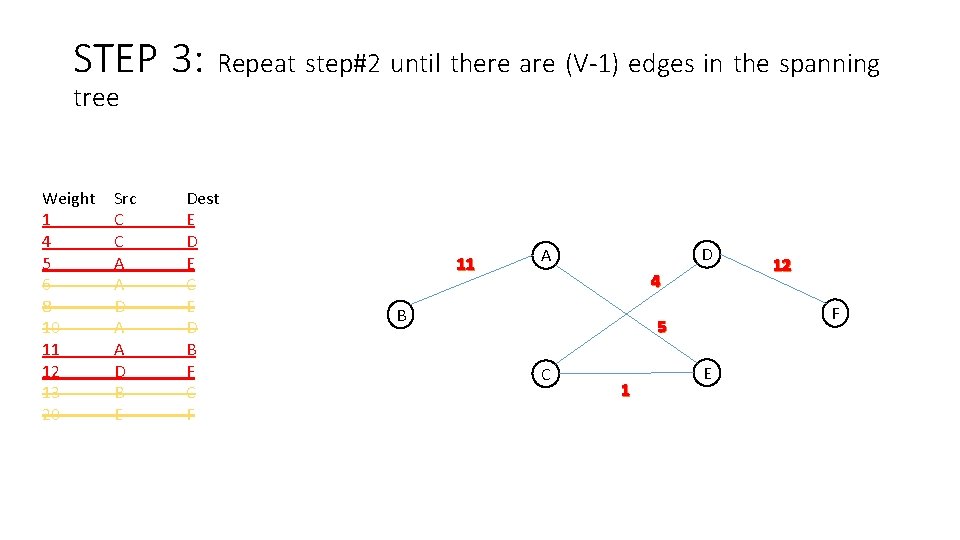
STEP 3: Repeat step#2 until there are (V-1) edges in the spanning tree Weight 1 4 5 6 8 10 11 12 13 20 Src C C A A D B E Dest E D E C E D B F C F 11 D A 4 B F 5 C 1 12 E

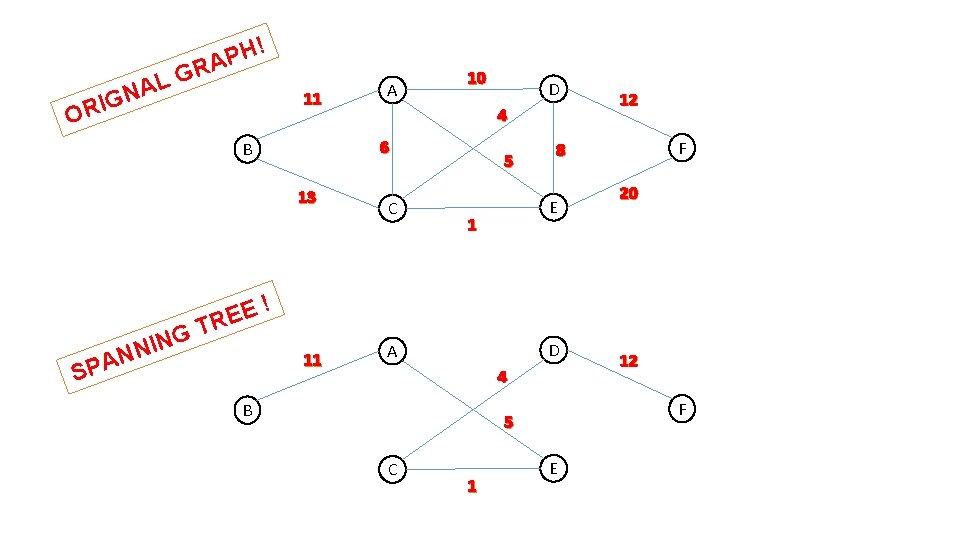
R G AL IGN OR ! H P A 11 13 SPA G 10 ! E TRE 11 D 4 6 B IN N N A C 5 D A 4 B 1 20 12 F 5 C F 8 E 1 12 E

MST Prim’s Algorithm 1. Remove all loops and parallel edges 2. Choose any arbitrary node as root node 3. Check outgoing edges and select the one with less cost 3. Repeat step#3 until there are (V-1) edges in the spanning tree.

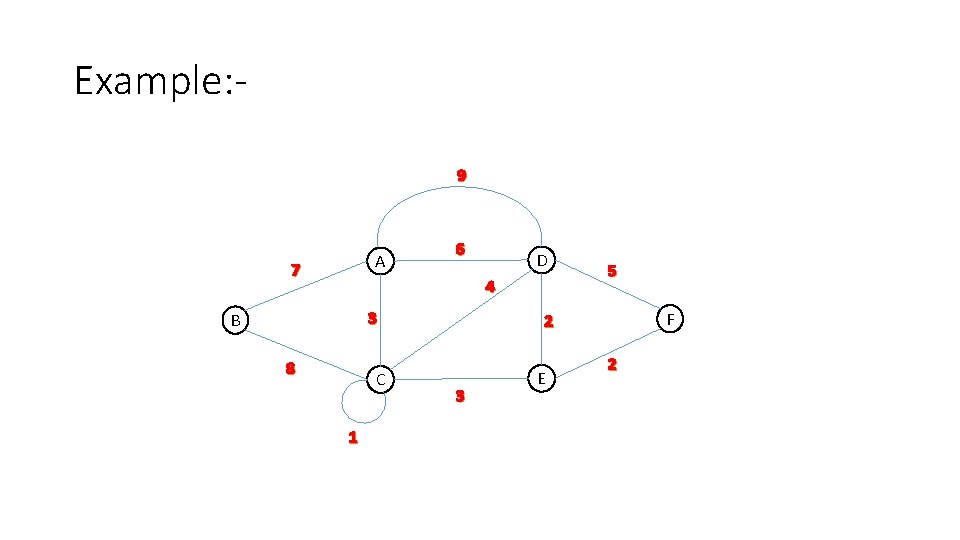
Example: 9 A 7 6 D 4 3 B 8 C 1 5 F 2 3 E 2

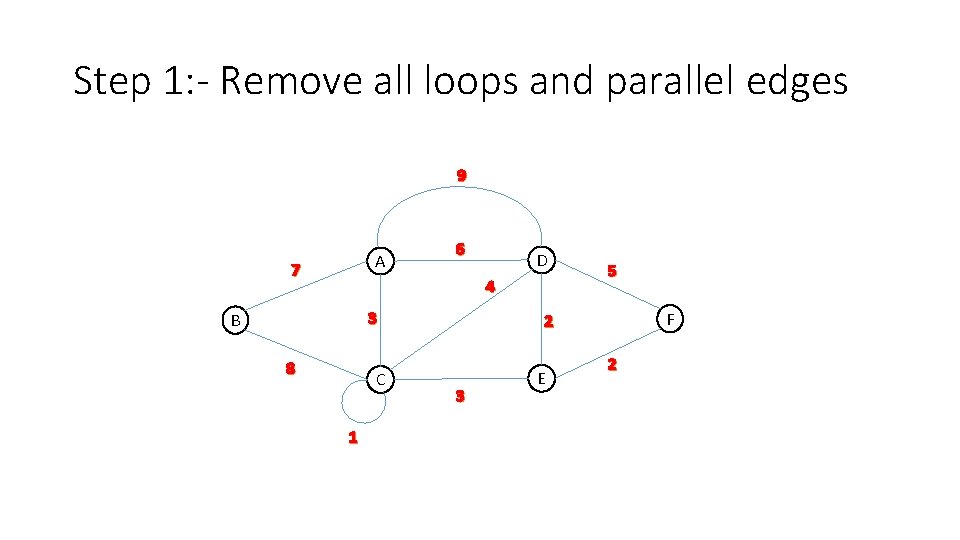
Step 1: - Remove all loops and parallel edges 9 A 7 6 D 4 3 B 8 C 1 5 F 2 3 E 2

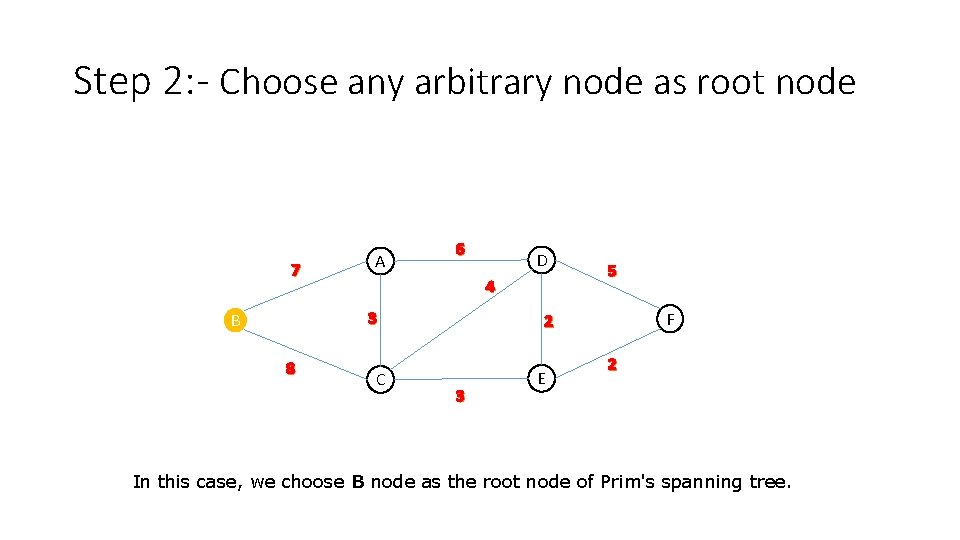
Step 2: - Choose any arbitrary node as root node 7 A 6 4 3 B 8 D C 5 F 2 3 E 2 In this case, we choose B node as the root node of Prim's spanning tree.

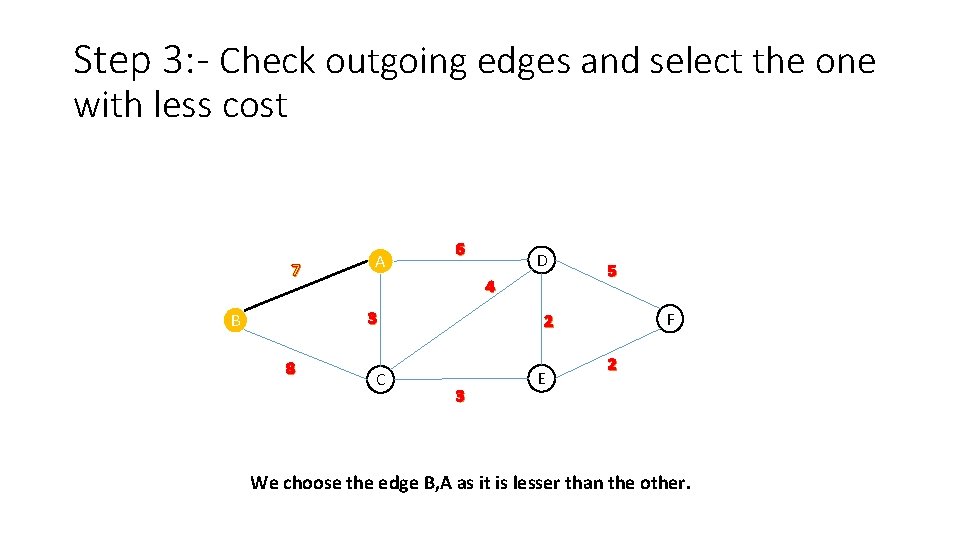
Step 3: - Check outgoing edges and select the one with less cost 7 A 6 4 3 B 8 D C 5 F 2 3 E 2 We choose the edge B, A as it is lesser than the other.

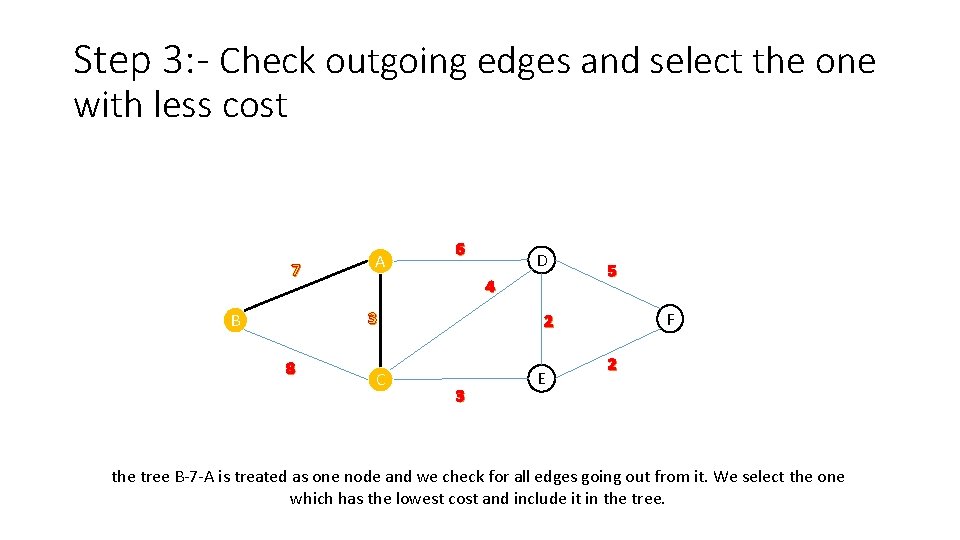
Step 3: - Check outgoing edges and select the one with less cost 7 A 6 4 3 B 8 D C 5 F 2 3 E 2 the tree B-7 -A is treated as one node and we check for all edges going out from it. We select the one which has the lowest cost and include it in the tree.

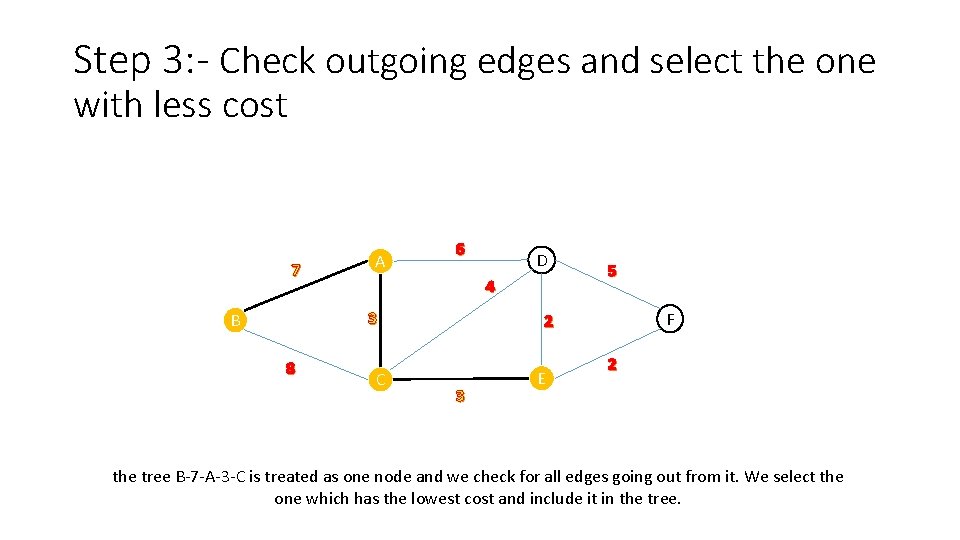
Step 3: - Check outgoing edges and select the one with less cost 7 A 6 4 3 B 8 D C 5 F 2 3 E 2 the tree B-7 -A-3 -C is treated as one node and we check for all edges going out from it. We select the one which has the lowest cost and include it in the tree.

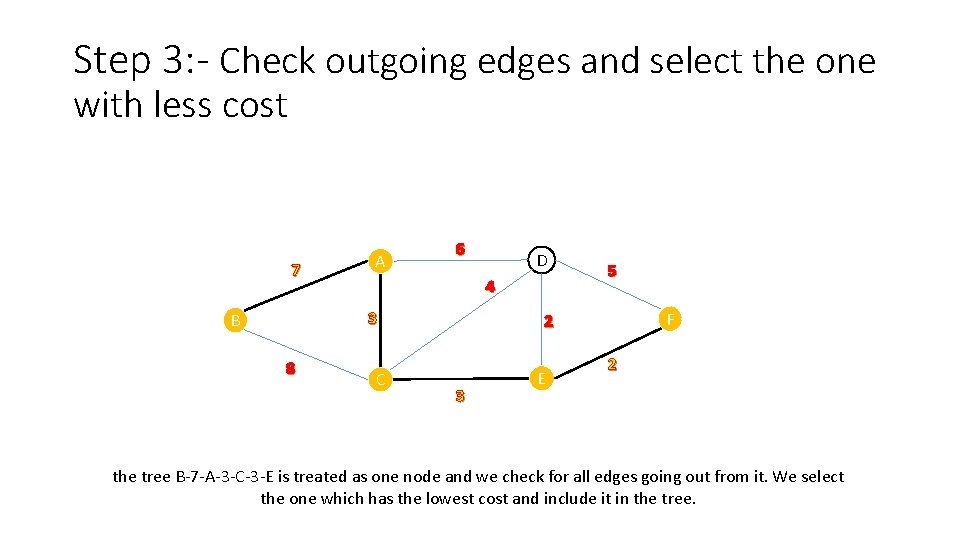
Step 3: - Check outgoing edges and select the one with less cost 7 A 6 4 3 B 8 D C 5 F 2 3 E 2 the tree B-7 -A-3 -C-3 -E is treated as one node and we check for all edges going out from it. We select the one which has the lowest cost and include it in the tree.

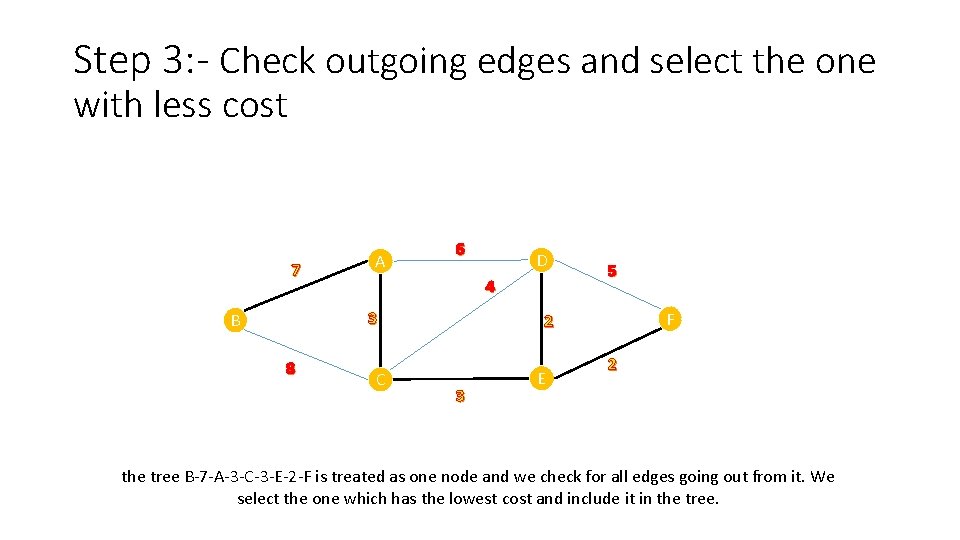
Step 3: - Check outgoing edges and select the one with less cost 7 A 6 4 3 B 8 D C 5 F 2 3 E 2 the tree B-7 -A-3 -C-3 -E-2 -F is treated as one node and we check for all edges going out from it. We select the one which has the lowest cost and include it in the tree.

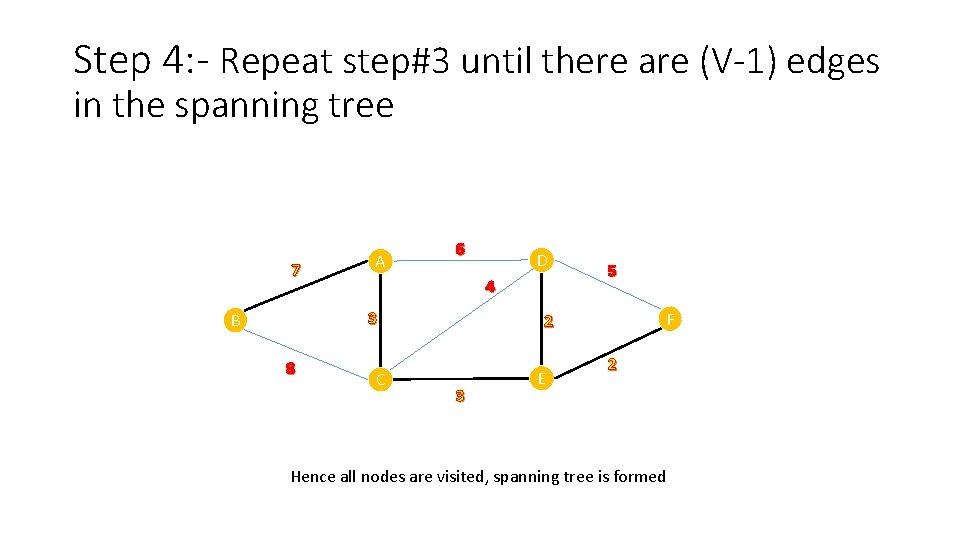
Step 4: - Repeat step#3 until there are (V-1) edges in the spanning tree 7 A 6 4 3 B 8 D C 5 F 2 3 E 2 Hence all nodes are visited, spanning tree is formed

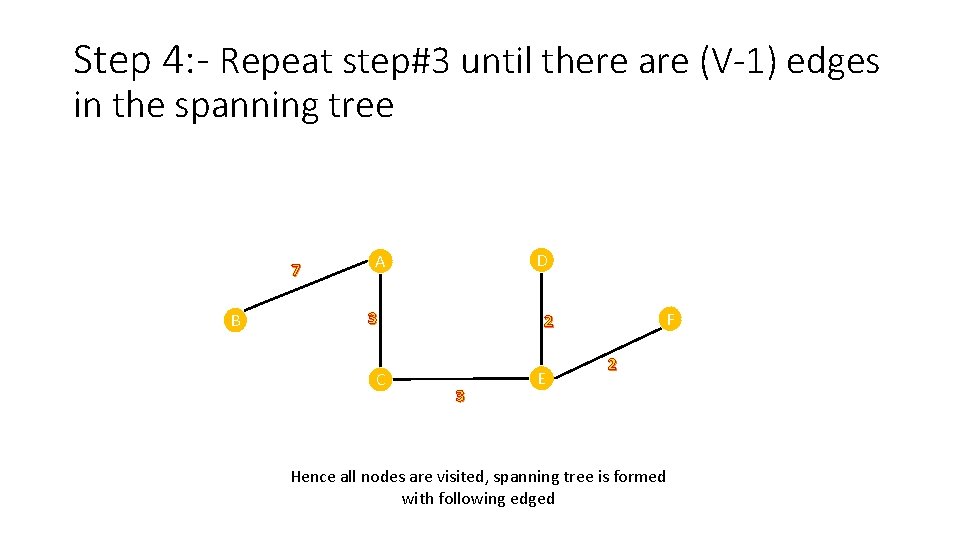
Step 4: - Repeat step#3 until there are (V-1) edges in the spanning tree 7 B D A 3 C F 2 3 E 2 Hence all nodes are visited, spanning tree is formed with following edged

ANY QUESTION ?