Minimum Spanning Tree Algorithms Prims Algorithm Copyright 1999

Minimum Spanning Tree Algorithms Prim’s Algorithm Copyright 1999 by Cutler/Head

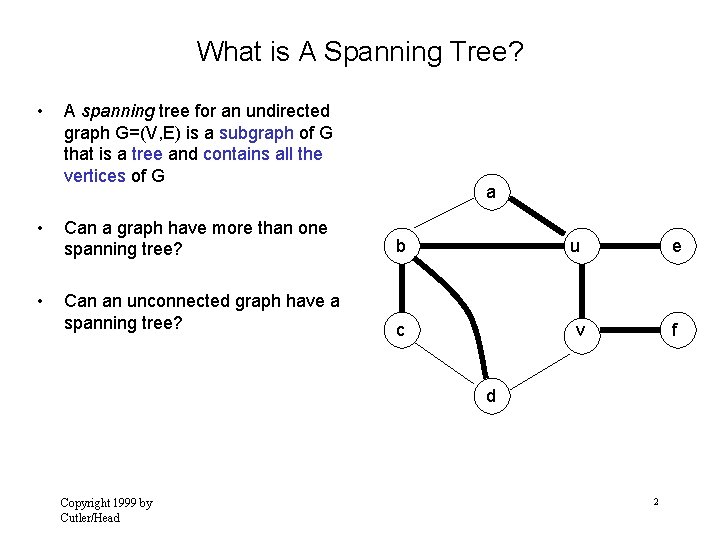
What is A Spanning Tree? • A spanning tree for an undirected graph G=(V, E) is a subgraph of G that is a tree and contains all the vertices of G a • Can a graph have more than one spanning tree? b u e • Can an unconnected graph have a spanning tree? c v f d Copyright 1999 by Cutler/Head 2

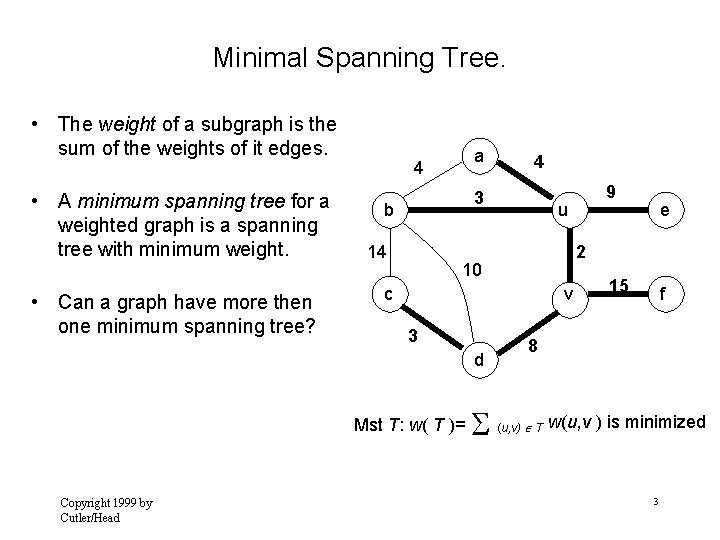
Minimal Spanning Tree. • The weight of a subgraph is the sum of the weights of it edges. • A minimum spanning tree for a weighted graph is a spanning tree with minimum weight. • Can a graph have more then one minimum spanning tree? a 4 3 b 14 v Mst T: w( T )= e 2 c 3 9 u 10 d Copyright 1999 by Cutler/Head 4 15 f 8 (u, v) T w(u, v ) is minimized 3

Example of a Problem that Translates into a MST The Problem • Several pins of an electronic circuit must be connected using the least amount of wire. Modeling the Problem • The graph is a complete, undirected graph G = ( V, E , W ), where V is the set of pins, E is the set of all possible interconnections between the pairs of pins and w(e) is the length of the wire needed to connect the pair of vertices. • Find a minimum spanning tree. Copyright 1999 by Cutler/Head 4

Greedy Choice We will show two ways to build a minimum spanning tree. • A MST can be grown from the current spanning tree by adding the nearest vertex and the edge connecting the nearest vertex to the MST. (Prim's algorithm) • A MST can be grown from a forest of spanning trees by adding the smallest edge connecting two spanning trees. (Kruskal's algorithm) • Another algorithm is a “backward” version of Kruskal. Edges are deleted in decreasing cost as long as graph remains connected. Copyright 1999 by Cutler/Head 5

Notation • Tree-vertices: in the tree constructed so far • Non-tree vertices: rest of vertices Prim’s Selection rule • Select the minimum weight edge between a treenode and a non-tree node and add to the tree Copyright 1999 by Cutler/Head 6

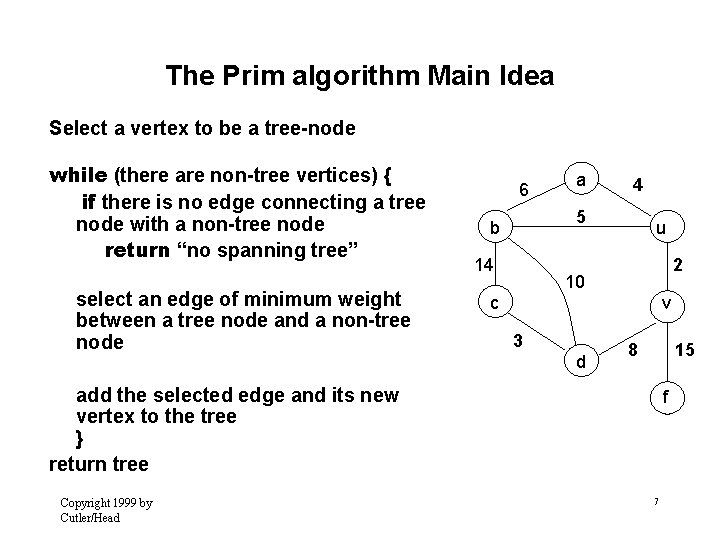
The Prim algorithm Main Idea Select a vertex to be a tree-node while (there are non-tree vertices) { if there is no edge connecting a tree node with a non-tree node return “no spanning tree” select an edge of minimum weight between a tree node and a non-tree node 6 a 4 5 b 14 u 2 10 c v 3 d 8 15 add the selected edge and its new vertex to the tree } return tree Copyright 1999 by Cutler/Head f 7

Implementation Issues • How is the graph implemented? – Assume that we just added node u to the tree. – The distance of non tree nodes adjacent to u may now be decreased. – There must be fast access to all the adjacent vertices. – So using adjacency lists seems better • How should the set of non-tree vertices be represented? – The operations are: • build set • delete node closest to tree • decrease the distance of a non-tree node from the tree • check whether a node is a non- tree node Copyright 1999 by Cutler/Head 8

Implementation Issues • How should the set of non-tree vertices be represented? – A priority queue PQ may be used with the priority D[v] equal to the minimum distance of each non-tree vertex v to the tree. – Each item in PQ contains: D[v], the vertex v, and the shortest distance edge (v, u) where u is a tree node • This means: – build a PQ of non-tree nodes with initial values • fast build heap O (V ) • building an unsorted list O(V) • building a sorted list O(V) (special case) Copyright 1999 by Cutler/Head 9

Implementation Issues – delete node closest to tree (extract. Min) • O(lg V ) if heap and • O(V) if unsorted list • O(1) sorted list – decrease the distance of a non-tree node to the tree – We need to find the location i of node v in the priority queue and then execute (decrease. Priority. Value(i, p)) where p is the new priority – decrease. Priority. Value(i, p) • O(lg V) for heap, • O(1) for unsorted list • O(V ) for sorted list (too slow) Copyright 1999 by Cutler/Head 10

Implementation Issues • What is the location i of node v in a priority queue? – Find in Heaps, and sorted lists O(n) – Unsorted – if the nodes are numbered 1 to n and we use an array where node v is the v item in the array O(1) Extended heap – We will use extended heaps that contain a “handle” to the location of each node in the heap. – When a node is not in PQ the “handle” will indicate that this is the case – This means that we can access a node in the extended heap in O(1), and check v PQ in O(1) – Note that the “handle” must be updated whenever a heap operation is applied Copyright 1999 by Cutler/Head 11

Implementation Issues 2. Unsorted list – Array implementation where node v can be accesses as PQ[v] in O(1), and the value of PQ[v] indicates when the node is not in PQ. Copyright 1999 by Cutler/Head 12

Prim’s Algorithm 1. for each u V 2. do D [u ] 3. D[ r ] 0 4. PQ make-heap(D, V, {})//No edges 5. T 6. 7. while PQ do 8. (u, e ) PQ. extract. Min() 9. add (u, e) to T 10. for each v Adjacent (u ) // execute relaxation 11. do if v PQ && w( u, v ) < D [ v ] 12. then D [ v ] w (u, v) 13. PQ. decrease. Priority. Value ( D[v], v, (u, v )) 14. return T // T is a mst. Copyright 1999 by Cutler/Head Lines 1 -5 initialize the priority queue PQ to contain all Vertices. Ds for all vertices except r, are set to infinity. r is the starting vertex of the T The T so far is empty Add closest vertex and edge to current T Get all adjacent vertices v of u, update D of each non-tree vertex adjacent to u Store the current minimum weight edge, and updated distance in the priority queue 13

Prim’s Algorithm Initialization Prim (G ) 1. for each u V 2. do D [u ] 3. D[ r ] 0 4. PQ make-heap(D, V, {})//No edges 5. T Copyright 1999 by Cutler/Head 14

Building the MST // solution check 7. while PQ do //Selection and feasibility 8. (u, e ) PQ. extract. Min() // T contains the solution so far. 9. add (u, e) to T 10. for each v Adjacent (u ) 11. do if v PQ && w( u, v ) < D [ v ] 12. then D [ v ] w (u, v) 13. PQ. decrease. Priority. Value (D[v], v, (u, v) ) 14. return T Copyright 1999 by Cutler/Head 15

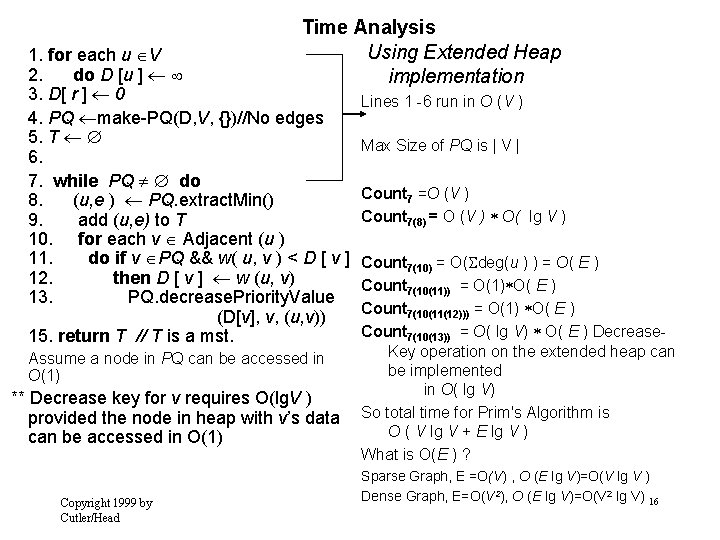
Time Analysis Using Extended Heap implementation 1. for each u V 2. do D [u ] 3. D[ r ] 0 4. PQ make-PQ(D, V, {})//No edges 5. T 6. 7. while PQ do 8. (u, e ) PQ. extract. Min() 9. add (u, e) to T 10. for each v Adjacent (u ) 11. do if v PQ && w( u, v ) < D [ v ] 12. then D [ v ] w (u, v) 13. PQ. decrease. Priority. Value (D[v], v, (u, v)) 15. return T // T is a mst. Assume a node in PQ can be accessed in O(1) ** Decrease key for v requires O(lg. V ) provided the node in heap with v’s data can be accessed in O(1) Copyright 1999 by Cutler/Head Lines 1 -6 run in O (V ) Max Size of PQ is | V | Count 7 =O (V ) Count 7(8) = O (V ) O( lg V ) Count 7(10) = O( deg(u ) ) = O( E ) Count 7(10(11)) = O(1) O( E ) Count 7(10(11(12))) = O(1) O( E ) Count 7(10(13)) = O( lg V) O( E ) Decrease. Key operation on the extended heap can be implemented in O( lg V) So total time for Prim's Algorithm is O ( V lg V + E lg V ) What is O(E ) ? Sparse Graph, E =O(V) , O (E lg V)=O(V lg V ) Dense Graph, E=O(V 2), O (E lg V)=O(V 2 lg V) 16

Time Analysis 1. for each u V 2. do D [u ] 3. D[ r ] 0 4. PQ make-PQ(D, V, {})//No edges 5. T 6. 7. while PQ do 8. (u, e ) PQ. extract. Min() 9. add (u, e) to T 10. for each v Adjacent (u ) 11. do if v PQ && w( u, v ) < D [ v ] 12. then D [ v ] w (u, v) 13. PQ. decrease. Priority. Value (D[v], v, (u, v)) 15. return T // T is a mst. Using unsorted PQ Lines 1 - 6 run in O (V ) Max Size of PQ is | V | Count 7 = O (V ) Count 7(8) = O (V ) O(V ) Count 7(10) = O( deg(u ) ) = O( E ) Count 7(10(11)) = O(1) O( E ) Count 7(10(11(12))) = O(1) O( E ) Count 7(10(13)) =O( 1) O( E ) So total time for Prim's Algorithm is O (V + V 2 + E ) = O (V 2 ) For Sparse/Dense graph : O( V 2 ) Note growth rate unchanged for adjacency matrix graph representation Copyright 1999 by Cutler/Head 17

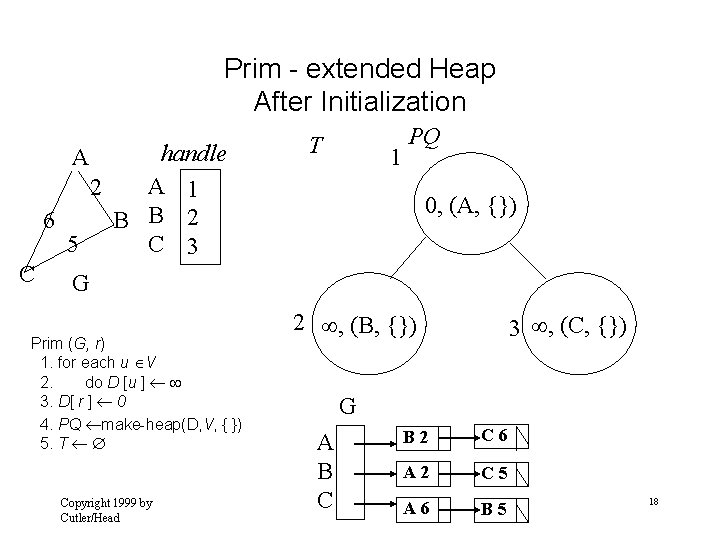
Prim - extended Heap After Initialization handle A 1 2 6 B B 2 5 C 3 A C T 1 PQ 0, (A, {}) G Prim (G, r) 1. for each u V 2. do D [u ] 3. D[ r ] 0 4. PQ make-heap(D, V, { }) 5. T Copyright 1999 by Cutler/Head 2 , (B, {}) 3 , (C, {}) G A B C B 2 C 6 A 2 C 5 A 6 B 5 18

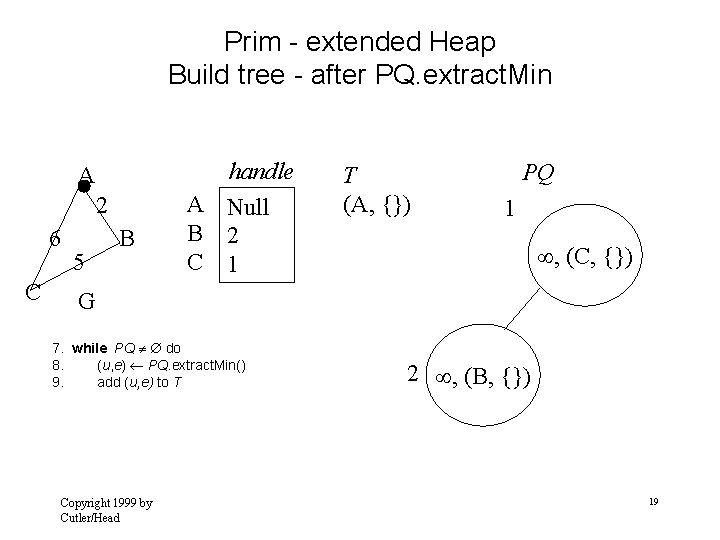
Prim - extended Heap Build tree - after PQ. extract. Min A 2 6 C 5 B handle A Null B 2 C 1 T (A, {}) PQ 1 , (C, {}) G 7. while PQ do 8. (u, e) PQ. extract. Min() 9. add (u, e) to T Copyright 1999 by Cutler/Head 2 , (B, {}) 19

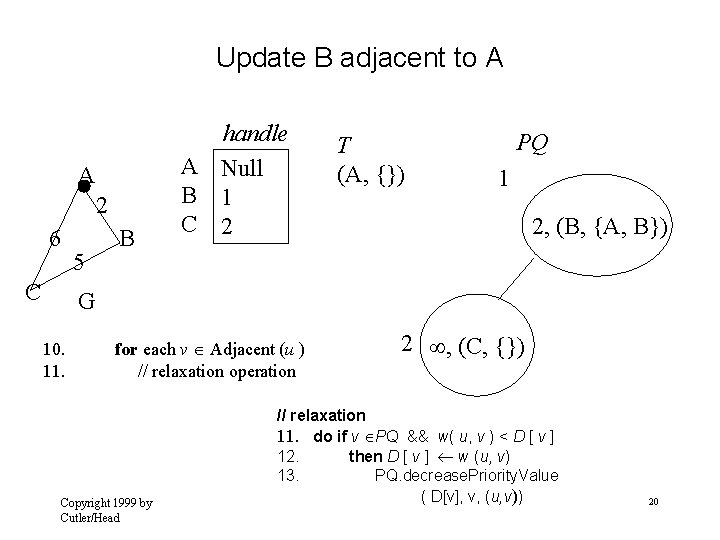
Update B adjacent to A A 2 6 C 5 B handle A Null B 1 C 2 T (A, {}) PQ 1 2, (B, {A, B}) G 10. 11. for each v Adjacent (u ) // relaxation operation Copyright 1999 by Cutler/Head 2 , (C, {}) // relaxation 11. do if v PQ && w( u, v ) < D [ v ] 12. then D [ v ] w (u, v) 13. PQ. decrease. Priority. Value ( D[v], v, (u, v)) 20

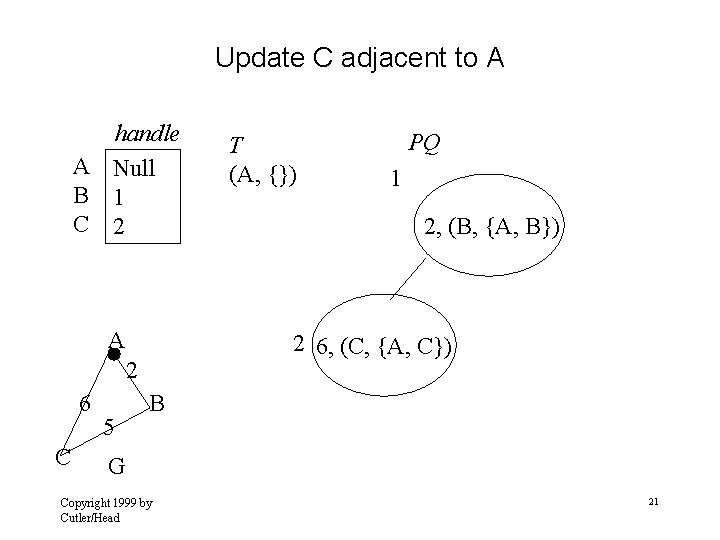
Update C adjacent to A handle A Null B 1 C 2 A C 5 PQ 1 2, (B, {A, B}) 2 6, (C, {A, C}) 2 6 T (A, {}) B G Copyright 1999 by Cutler/Head 21

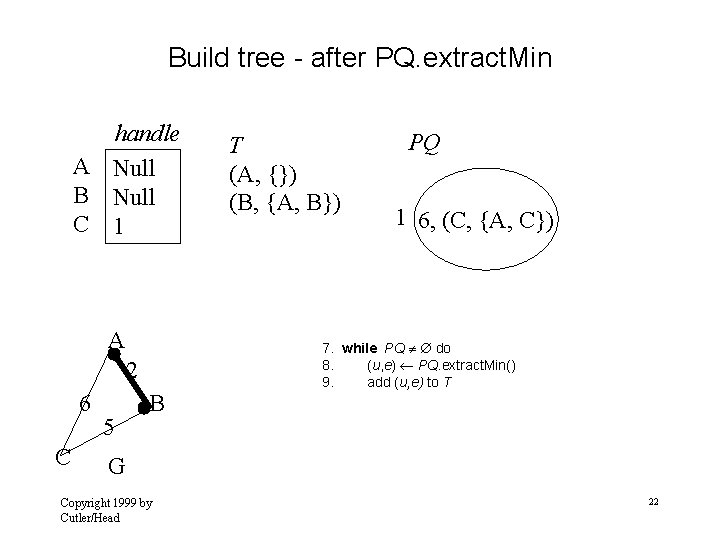
Build tree - after PQ. extract. Min handle A Null B Null C 1 A 2 6 C 5 B T (A, {}) (B, {A, B}) PQ 1 6, (C, {A, C}) 7. while PQ do 8. (u, e) PQ. extract. Min() 9. add (u, e) to T G Copyright 1999 by Cutler/Head 22

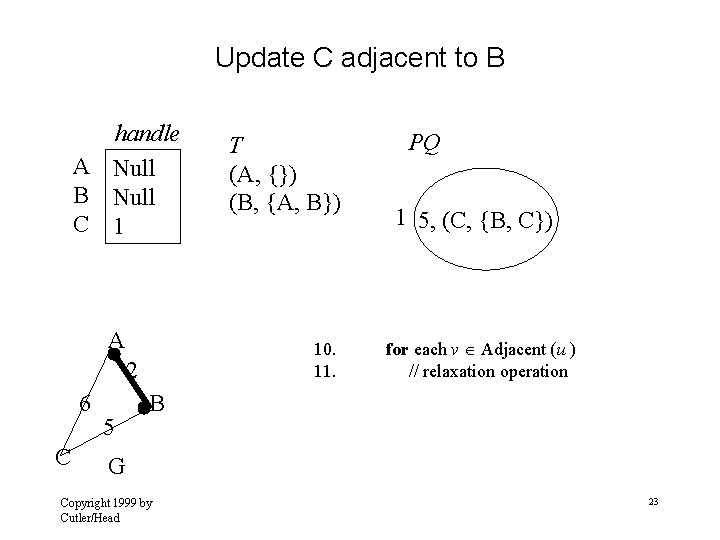
Update C adjacent to B handle A Null B Null C 1 A 10. 11. 2 6 C 5 T (A, {}) (B, {A, B}) PQ 1 5, (C, {B, C}) for each v Adjacent (u ) // relaxation operation B G Copyright 1999 by Cutler/Head 23

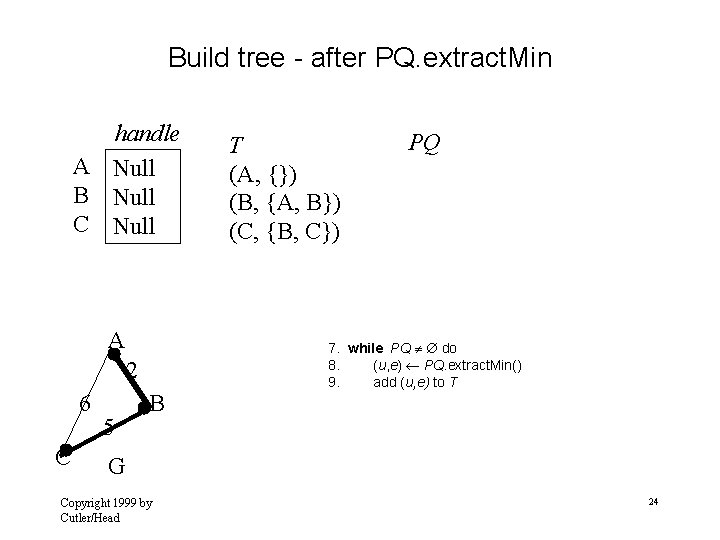
Build tree - after PQ. extract. Min handle A Null B Null C Null A 2 6 C 5 B T (A, {}) (B, {A, B}) (C, {B, C}) PQ 7. while PQ do 8. (u, e) PQ. extract. Min() 9. add (u, e) to T G Copyright 1999 by Cutler/Head 24

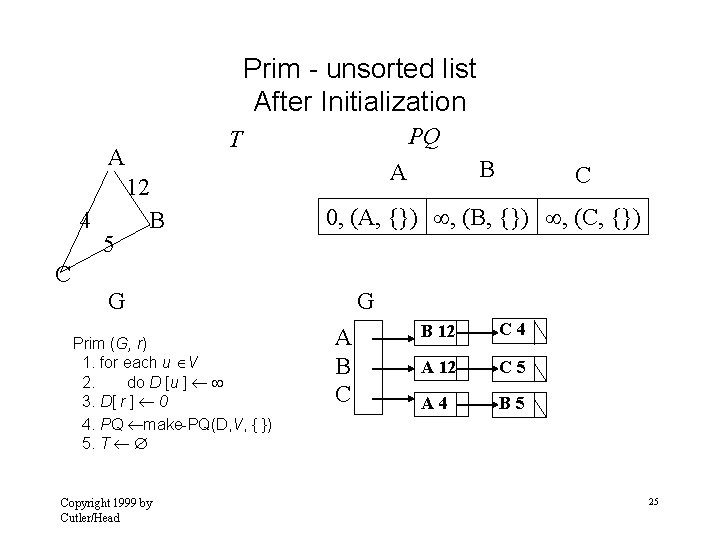
Prim - unsorted list After Initialization A 4 5 PQ T 12 B B A C 0, (A, {}) , (B, {}) , (C, {}) C G Prim (G, r) 1. for each u V 2. do D [u ] 3. D[ r ] 0 4. PQ make-PQ(D, V, { }) 5. T Copyright 1999 by Cutler/Head G A B C B 12 C 4 A 12 C 5 A 4 B 5 25

Build tree - after PQ. extract. Min A 4 5 12 B T (A, {}) PQ A B C Null , (B, {}) , (C, {}) C G 7. while PQ do 8. (u, e) PQ. extract. Min() 9. add (u, e) to T Copyright 1999 by Cutler/Head 26

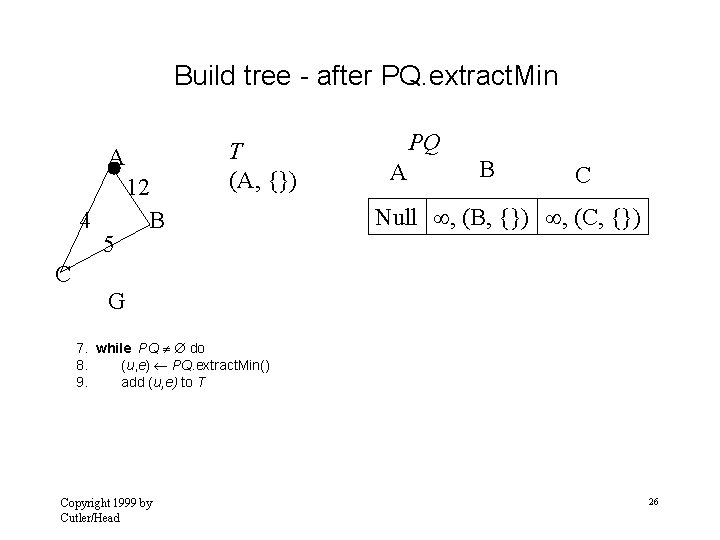
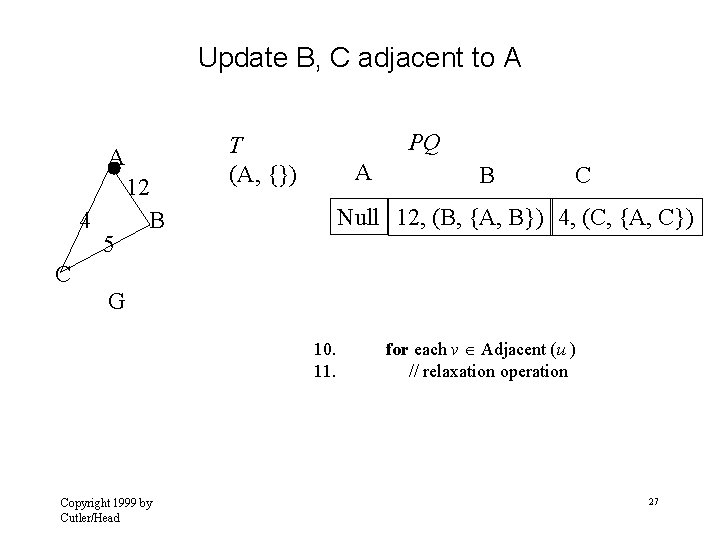
Update B, C adjacent to A A 4 5 12 B PQ T (A, {}) A B C Null 12, (B, {A, B}) 4, (C, {A, C}) C G 10. 11. Copyright 1999 by Cutler/Head for each v Adjacent (u ) // relaxation operation 27

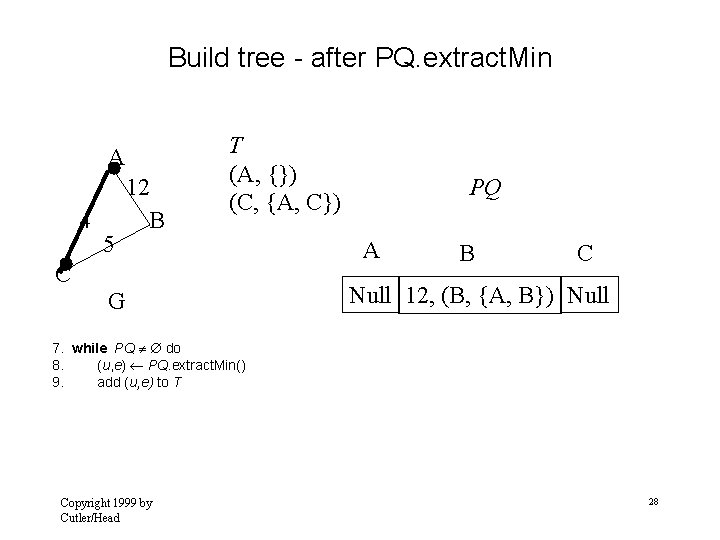
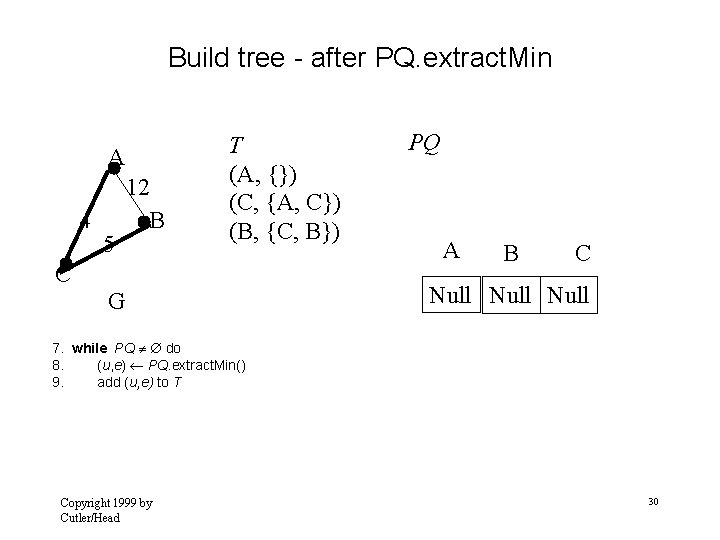
Build tree - after PQ. extract. Min A 4 5 12 B T (A, {}) (C, {A, C}) C G PQ A B C Null 12, (B, {A, B}) Null 7. while PQ do 8. (u, e) PQ. extract. Min() 9. add (u, e) to T Copyright 1999 by Cutler/Head 28

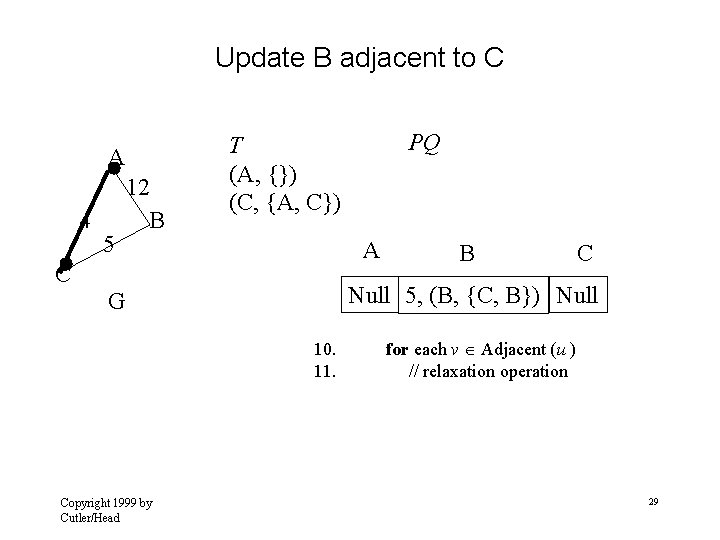
Update B adjacent to C A 4 5 12 B A C B C Null 5, (B, {C, B}) Null G 10. 11. Copyright 1999 by Cutler/Head PQ T (A, {}) (C, {A, C}) for each v Adjacent (u ) // relaxation operation 29

Build tree - after PQ. extract. Min A 4 5 12 B T (A, {}) (C, {A, C}) (B, {C, B}) C G PQ A B C Null 7. while PQ do 8. (u, e) PQ. extract. Min() 9. add (u, e) to T Copyright 1999 by Cutler/Head 30

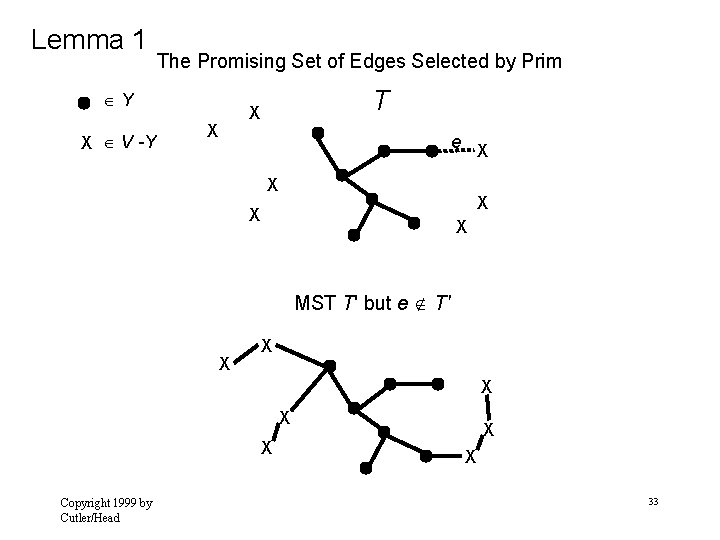
Lemma 1 Let G = ( V, E) be a connected, weighted undirected graph. Let T be a promising subset of E. Let Y be the set of vertices connected by the edges in T. If e is a minimum weight edge that connects a vertex in Y to a vertex in V - Y, then T { e } is promising. Note: A feasible set is promising if it can be extended to produce not only a solution , but an optimal solution. In this algorithm: A feasible set of edges is promising if it is a subset of a Minimum Spanning Tree for the connected graph. Copyright 1999 by Cutler/Head 31

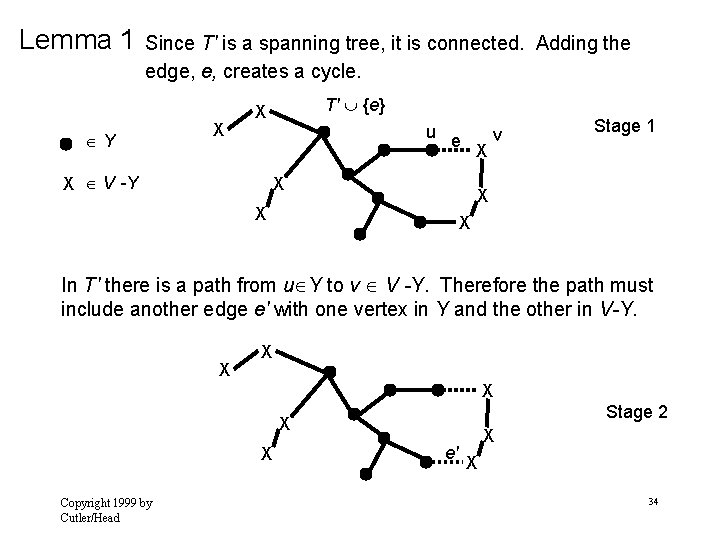
Outline of Proof of Correctness of Lemma 1 T is the promising subset, and e the minimum cost edge of Lemma 1 Let T ' be the MST such that T T ' We will show that if e T' then there must be another MST T" such that T {e} T". Proof has 4 stages: 1. Adding e to T', closes a cycle in T' {e}. 2. Cycle contains another edge e' T' but e' T 3. T"=T' {e} - {e’ } is a spanning tree 4. T" is a MST Copyright 1999 by Cutler/Head 32

Lemma 1 The Promising Set of Edges Selected by Prim Y X V -Y T X X e X X X MST T' but e T' X X X Copyright 1999 by Cutler/Head X X 33

Lemma 1 Since T' is a spanning tree, it is connected. Adding the edge, e, creates a cycle. Y X T' {e} X u X V -Y e X X v Stage 1 X X X In T' there is a path from u Y to v V -Y. Therefore the path must include another edge e' with one vertex in Y and the other in V-Y. X X X Stage 2 X X Copyright 1999 by Cutler/Head e' X X 34

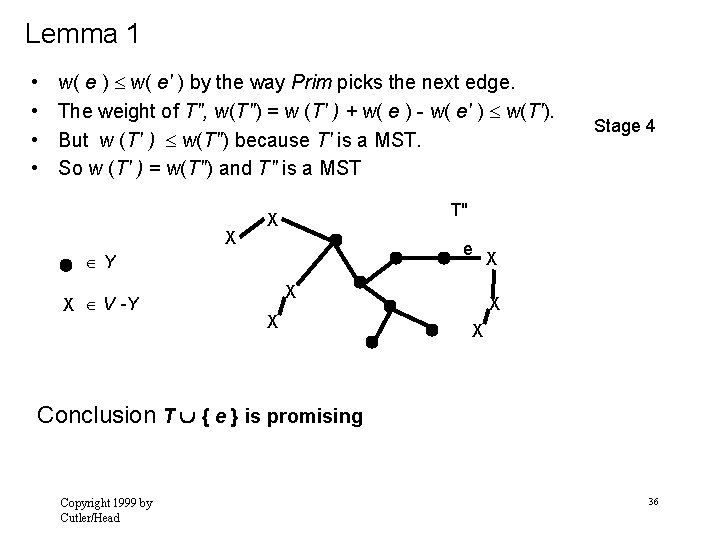
Lemma 1 • If we remove e’ from T’ { e } the cycle disappears. • T”=T’ { e } - {e’} is connected. T’ is connected. Every pair of vertices connected by a path that does not include e’ is still connected in T”. Every pair of vertices connected by a path that included e’ , is still connected in T” because there is a path in T" =T’ { e } - { e’ } connecting the vertices of e’. X T" X e Y X V -Y Stage 3 X X X w( e ) w( e' ) By the way Prim picks the next edge Copyright 1999 by Cutler/Head 35

Lemma 1 • • w( e ) w( e' ) by the way Prim picks the next edge. The weight of T", w(T") = w (T' ) + w( e ) - w( e' ) w(T'). But w (T' ) w(T") because T' is a MST. So w (T' ) = w(T") and T" is a MST X T" X e Y X V -Y Stage 4 X X X Conclusion T { e } is promising Copyright 1999 by Cutler/Head 36

Theorem : Prim's Algorithm always produces a minimum spanning tree. Proof by induction on the set T of promising edges. Base case: Initially, T = is promising. Induction hypothesis: The current set of edges T selected by Prim is promising. Induction step: After Prim adds the edge e, T { e } is promising. Proof: T { e } is promising by Lemma 1. Conclusion: When G is connected, Prim terminates with |T | = |V | -1, and T is a MST. Copyright 1999 by Cutler/Head 37