Minimum cost spanning tree and activity networks Data

Minimum cost spanning tree and activity networks Data structure 2002/12/2

Minimum-cost spanning trees (MST) in a given graph (6. 3) • A minimum-cost spanning tree is a spanning tree • of least cost Design strategy – greedy method – Kruskal’s algorithm • Edge by edge – Prim’s algorithm • Span out from one vertex – Sollin’s algorithm • Hint: Construct from connected components • Leave as a homework

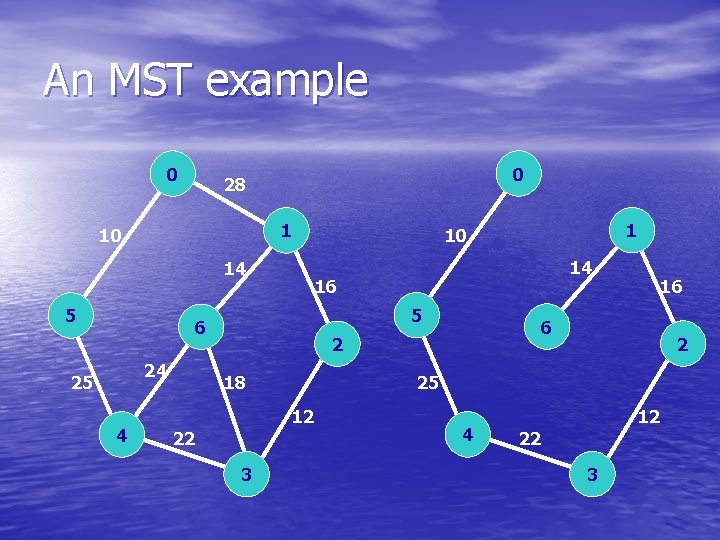
An MST example 0 0 28 1 10 14 5 24 4 14 16 5 6 25 2 25 18 12 3 16 6 2 22 1 10 4 12 22 3

Kruskal’s algorithm • Edge by edge • O(e log e) • Algorithm: T={}; While ((T contains less than n-1 edges) &&(E not empty)){ choose an edge (v, w) from E of lowest cost; delete (v, w) from E; if((v, w) does not create a cycle in T) add(v, w) to T; else discard(v, w); } If(T contains fewer than n – 1 edges) printf(“No spanning treen”);

Prim’s algorithm • Begins from a vertex • O(n 2) • Algorithm: T={}; TV = {0}; /* start with vertex 0 and no edges */ While (T contains fewer than n-1 edges){ let(u, v) be a least cost edge s. t. u in TV and v not in TV; if (there is no such edge) break; add v to TV; add (u, v) to T; } If (T contains fewer than n-1 edges) printf(“No spanning treen”);

Activity networks (6. 5) • Definition: – Vertex i is a predecessor of j • Iff there is a directed path from i to j – Vertex i is an immediate predecessor of j • Iff <i, j> is an edge in G – Successor, immediate successor – Precedence relation, is a partial order relation • Transitive • Irreflexive • Can be represented by a Directed Acyclic Graph (DAG)? – Topological order • is a linear ordering of the vertices of a graph s. t. if i is a predecessor of j, then i precedes j in the linear ordering

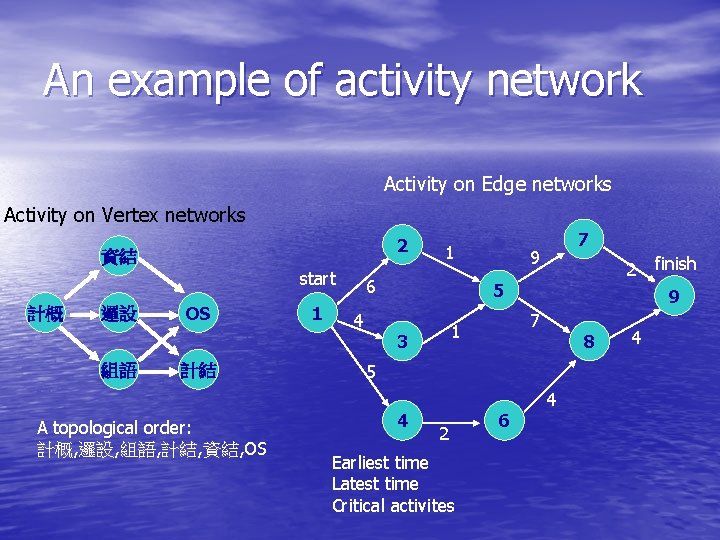
An example of activity network Activity on Edge networks Activity on Vertex networks 2 資結 start 計概 邏設 組語 OS 計結 A topological order: 計概, 邏設, 組語, 計結, 資結, OS 1 1 6 4 7 9 2 5 3 9 7 1 8 5 4 2 Earliest time Latest time Critical activites 6 finish 4 4