Minimum Cost Flow Algorithms and Networks This lecture

Minimum Cost Flow Algorithms and Networks

This lecture • The minimum cost flow problem: statement and applications • The cycle cancelling algorithm • A polynomial time variant of cycle cancelling • The successive shortest paths algorithm 2 Algorithms and Networks: Minimum Cost Flow

Minimum Cost Flow I • Edges have – Capacity: c(u, v): bound on amount of flow that can go through the edge – Cost: cost(u, v): cost that must be paid per unit of flow that goes through the edge. • Cost of flow f: – Sum over all (u, v) of: f (u, v) * cost(u, v). 3 Algorithms and Networks: Minimum Cost Flow

Minimum cost flow problem • Given: Network G, c, cost, s, t, and a target flow value r. • Question: Find a flow from s to t with value r, with minimum cost. 4 Algorithms and Networks: Minimum Cost Flow

Unbounded capacities • Some edges may have unbounded capacities – If there is a cycle of negative cost with only edges with unbounded capacity: • Arbitrary small cost (degenerate case) • Finding such a cycle: shortest paths algorithms (see lectures by Johan) – Otherwise: simple transformation to bounded capacities • E. g. , set each unbounded capacity to sum of all bounded capacities 5 Algorithms and Networks: Minimum Cost Flow

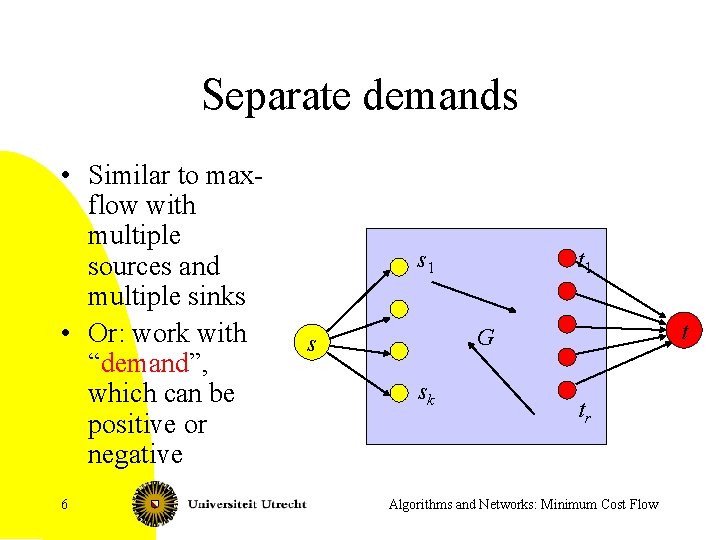
Separate demands • Similar to maxflow with multiple sources and multiple sinks • Or: work with “demand”, which can be positive or negative 6 s 1 t G s sk tr Algorithms and Networks: Minimum Cost Flow

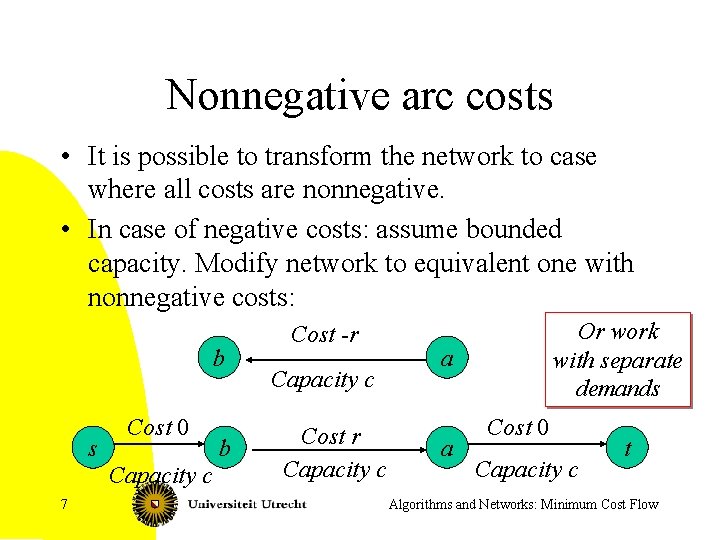
Nonnegative arc costs • It is possible to transform the network to case where all costs are nonnegative. • In case of negative costs: assume bounded capacity. Modify network to equivalent one with nonnegative costs: b s Cost 0 Capacity c 7 b Cost -r Capacity c Cost r Capacity c Or work with separate demands a a Cost 0 Capacity c t Algorithms and Networks: Minimum Cost Flow

Applications • Transport problems • Minimum cost matchings • Reconstruction of Left Ventricle from X-ray projections – Image: 2 d bit array; known are sums of columns, rows; probabilities for each bit – Look for image with correct row and column sums of maximum probability – Can be modelled as minimum cost flow problem 8 Algorithms and Networks: Minimum Cost Flow

Application: Optimal loading of hopping airplane 1 2 n bij weight units (or passengers) can be transported from i to j Each gives a profit of fij Plane can never carry more than p units How much units do we transport of each type for maximum profit? 14 13 12 1 9 Capacity i ® j: p 24 Node ij has supply bij Cost from ij to i: - fij 23 34 Node i has demand sum over all bji 2 3 4 All other arcs infinite cap. All other costs 0 Algorithms and Networks: Minimum Cost Flow

Cycles and circulations; paths and flows • We can view: – Cycles as a special type of circulations – Paths as a special type of flows – If we have a directed cycle c, then we can see it as a circulation: • c(e) = 1 when e is on c • c(e) = 0 otherwise – If we have a path p from s to t, we can see it as a flow with value 1: • p(e) = 1 when e is on p • p(e) = 0 otherwise 10 Algorithms and Networks: Minimum Cost Flow

First: useful theorems on flows and circulations Theorem Let f be a circulation. Then f is a nonnegative linear combination of cycles in G. Proof. • Ignore lower bounds. • If f(v, w) = 0 everywhere, then it clearly holds. • Otherwise, there is a directed cycle c in G with each edge e on c: f(e)>0 • Let r be the minimum flow of an edge on c, i. e. , r = min {f(e) | e on c} • Use induction: theorem also holds for f – cr: f-cr(e) = f(e) when e is not on c f-cr(e) = f(e) – r when e is on c • … 11 A&N: Maximum flow

Corollary for flows • Corollary: Let f be a flow from s to t. f is a nonnegative linear combination of cycles in G and paths from s to t. • Proof: Add edge from t to s with flow equal to value(f). Now, we have a circulation. Apply previous theorem. Cycles that use (t, s) correspond to a path from s to t. … QED 12 Algorithms and Networks: Minimum Cost Flow

More on these linear combinations • If circulation f is integer, then f can be written as an`integer scalared’ linear combination of cycles in G • A flow f with each f(e) an integer is the integer scalared linear combination of cycles and paths from s to t 13 Algorithms and Networks: Minimum Cost Flow

Algorithms for finding minimum cost flow • Here: two simple algorithms, based on the residual network • Better algorithms exist, see also the exercise sets 14 Algorithms and Networks: Minimum Cost Flow

Residual network • Define the residual network Gf of a flow f – Capacities as for maximum flow algorithms – If f (u, v)>0, then costf (u, v) = cost(u, v), and costf (v, u) = – cost(u, v). 15 Algorithms and Networks: Minimum Cost Flow

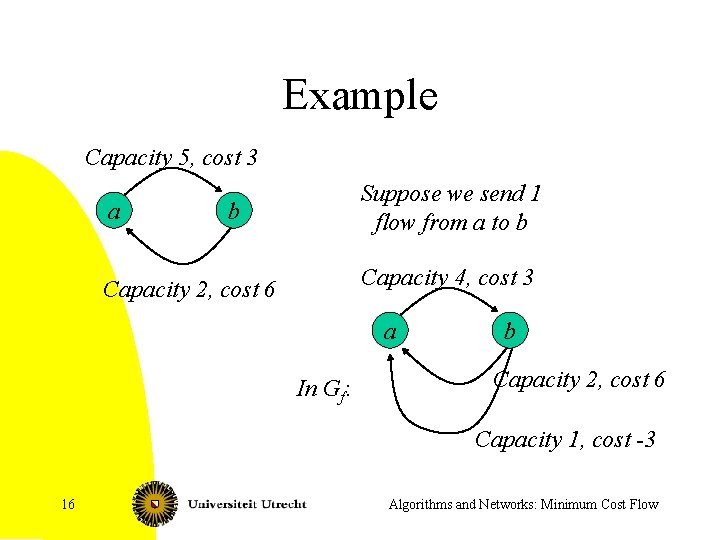
Example Capacity 5, cost 3 a Suppose we send 1 flow from a to b b Capacity 4, cost 3 Capacity 2, cost 6 a In Gf: b Capacity 2, cost 6 Capacity 1, cost -3 16 Algorithms and Networks: Minimum Cost Flow

Cycle cancelling algorithm • Make a feasible flow f in the network • while Gf has a negative cycle do – Find a negative cycle C in Gf – Let D be the minimum residual capacity cf of an edge on C – Add D units of flow to each edge on C: this is a new feasible flow of smaller cost • Output f. 17 Algorithms and Networks: Minimum Cost Flow

Cycle cancelling algorithm is correct • Theorem: a flow f has minimum costs, if and only if Gf has no negative cycle. • Proof: – If Gf has negative cycle, then we can improve f to one with smaller cost. – Suppose f is a flow, and f’ is an optimal flow. f’ – f is a circulation in Gf, hence a linear combination of cycles, and if f is not optimal, then the total cost of these cycles is negative, so there is a negative cycle in this set: it is a cycle in Gf. 18 Algorithms and Networks: Minimum Cost Flow

More on the cycle cancelling algorithm • No guarantee that it uses polynomial time. • Corollary: if all capacities and target flow value are integral, then there is an optimal integer minimum cost flow. – The cycle cancelling algorithm finds an integer flow in this case. • Variant: using always the minimum mean cost cycle gives a polynomial time algorithm! 19 Algorithms and Networks: Minimum Cost Flow

Minimum mean-cost circulation algorithm • Cycle cancelling algorithm but find always the minimum mean cost cycle and use that. – O(nm) time to find the cycle. – A theorem shows that O(nm 2 log 2 n) iterations are sufficient. – O(n 2 m 3 log 2 n) algorithm. 20 Algorithms and Networks: Minimum Cost Flow

Lower bounds • Cycle cancelling algorithm also works with lower bounds: – First find a feasible flow, respecting lower bounds (see lecture on max flow) – Remaining algorithm the same, with the residual network defined as for flows with lower bounds 21 Algorithms and Networks: Minimum Cost Flow

Successive shortest paths • Start with flow f with f(u, v)=0 for all u, v. • repeat until value(f ) = r – Find the shortest path P in Gf from s to t – Let q be the minimum residual capacity of an edge on P. – Send min(q, r – value(f)) additional units of flow across P. 22 Algorithms and Networks: Minimum Cost Flow

Time and correctness • Time: possibly exponential time … • Correctness: only if G has no cycle with negative cost • If G has a negative cycle, the algorithm may give an incorrect answer, e. g. , when we have target flow r=0 • Proof of correctness: next 23 Algorithms and Networks: Minimum Cost Flow

Correctness of successive shortest paths algorithm • Theorem: If G has no negative cycle, then the successive shortest paths algorithm gives the minimum cost flow. • Proof follows from • Claim: The ssp-algorithm maintains the following invariant: f has minimum cost among all flows with value(f). 24 Algorithms and Networks: Minimum Cost Flow

Proof of claim • Suppose we obtain f’ from f by sending flow over a path P. • From invariant: f has minimum cost for flows with value equal to value(f) • Suppose f’’ is a minimum cost flow with same value as f’. • f’’ – f is a flow in Gf. Hence, it can be written as a linear combination of cycles in Gf and paths from s to t in Gf. – All cycles in Gf have cost at least 0: otherwise f is not of minimum cost – All paths in this combination have cost at least the cost of P: this is how the algorithm works (P is shortest path) – It follows that cost(f’’ – f) >= cost (f’ – f) – So, cost(f’’) >= cost(f’) which show minimality of cost of f’. • QED 25 Algorithms and Networks: Minimum Cost Flow

Finally • More efficient algorithms exist – Some use scaling techniques: • Scaling on capacities • Scaling on costs – Scaling will be discussed in the chapter on shortest paths 26 Algorithms and Networks: Minimum Cost Flow