Minimum Classification Error MCE Approach in Pattern Recognition

Minimum Classification Error (MCE) Approach in Pattern Recognition Wu Chou, Avaya Labs Research, Avaya Inc. , USA Present by: Fang-Hui Chu

Outline (1/2) • • Introduction Optimal Classifier from Bayes Desicion Theory Discriminant Function Approach to Classifier Design Speech Recogniation and Hidden Markov Modeling – Hidden Markov Modeling of Speech • MCE Classifier Design Using Discriminant Functions – – – MCE Classifier Design Strategy Optimization Methods Other Optimization Methods HMM as a Discriminant Function Relation Between MCE and MMI Discussions and Comments 2

Outline (2/2) • MCE TRAINING BASED ON EMBEDDED STRING MODEL – String-Model-Based MCE Approach – Combined String-Model-Based MCE Approach – Discriminative Language Model Estimation • SUMMARY 3

Introduction • The advent of powerful computing devices and success of statistical approaches – A renewed pursuit for more powerful method to reduce recognition error rate • Although MCE-based discriminative methods is rooted in the classical Bayes’ decision theory, instead of a classification task to distribution estimation problem, it takes a discriminant-function based statistical pattern classification approach • For a given family of discriminant function, optimal classifier/recognizer design involves finding a set of parameters which minimize the empirical pattern recognition error rate 4

Introduction • Why we take this approach to design classifier? – We lack complete knowledge of the form of the distribution – Training data are inadequate • How to do? – Formulating the problem of self-learning into a classification problem which consists of optimal partitioning of the observation space into regions, Xk, for which the expected risk , R, is minimized – Then we apply generalized probabilistic decent algorithm to achieve the goal 5

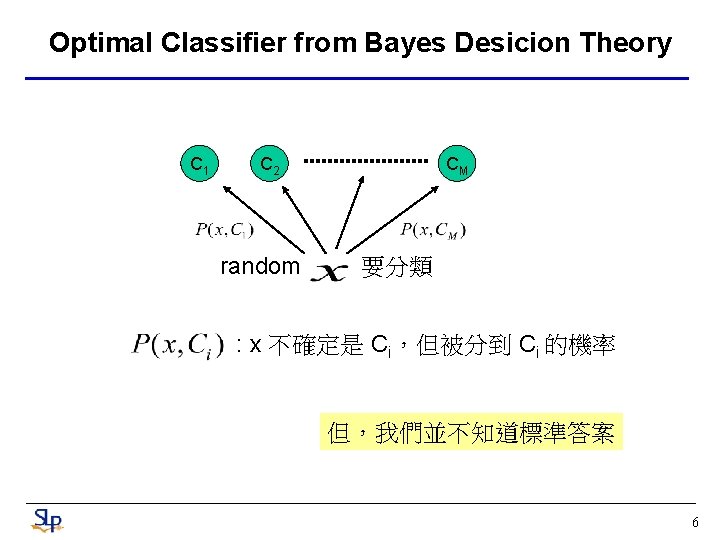
Optimal Classifier from Bayes Desicion Theory C 1 C 2 random CM 要分類 : x 不確定是 Ci，但被分到 Ci 的機率 但，我們並不知道標準答案 6

Optimal Classifier from Bayes Desicion Theory 定義 loss function : 可以想成 Class i 與 Class j 的 distance, 將 Class i 的observation分到 Class j，分錯的 cost 假設 Class i 是正確答案， 則將 x 分錯而得到的cost之expectation (1) 7

Optimal Classifier from Bayes Desicion Theory 在SR及許多application中，我們常用的 loss function Posterior Probability (5) 所以【Decision Rule】可以改寫 Bayes’ risk (6) MAP decision 9

Optimal Classifier from Bayes Desicion Theory OK!! 若 Posterior Probability知道，一切好辦 over 但一般來說，Posterior Probability 需有已知 class 的 labeled training data來估測 (這是不容易取得的) 本來是classifier design的問題 distribution estimation problem estimate the a posterior probabilities for any to implement the maximum a posterior decision for minimum Bayes risk 由Bayes’ Theorem (7) 可省略！ 10

Optimal Classifier from Bayes Desicion Theory • three issues： – The distribution form is often limited by the mathematical tractability of the particular distribution functions and is very likely to be inconsistent with the actual distribution – The estimation method has to be able to produce consistent parameter values when the size of the training samples varies – Requiring a training data set of sufficient size in order to have reliable parameter estimates • But in practice and for speech and language processing in particular, training data are always sparse 11

Optimal Classifier from Bayes Desicion Theory • Despite the conceptual optimality of the Bayes decision theory and its applications to pattern recognition, it can’t always be accomplished in practice • Most practical “MAP” decisions in speech and language processing are not true MAP decisions 12

Discriminant Function Approach to Classifier Design 先只考慮 2 -class 定義 discriminant function 分類用 One well-studied family of discriminant function is the Linear discriminant function which has computational advantages (9) 13

Discriminant Function Approach to Classifier Design More generally (10) (11) 14

Discriminant Function Approach to Classifier Design 再來考慮 M-class (12) 也就是說，我們要一組『最佳discriminant functions』 (13) When the loss function is specified 15

Discriminant Function Approach to Classifier Design This is quite different from the distribution estimation based approach in pattern classification 16

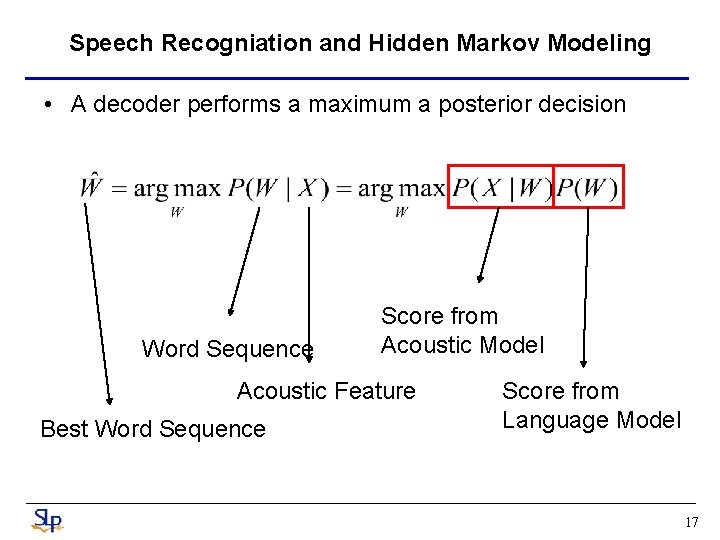
Speech Recogniation and Hidden Markov Modeling • A decoder performs a maximum a posterior decision Word Sequence Score from Acoustic Model Acoustic Feature Best Word Sequence Score from Language Model 17

Speech Recogniation and Hidden Markov Modeling • Basic components: • Acoustic Feature Extraction： – Used to extract the features from waveform. – We use to represent the acoustic observation feature vector sequence. • Acoustic Modeling： – Provides statistical modeling for the acoustic observation X. – Hidden Markov Model is the prevalent choice. • Language Modeling： – Provides linguistic constraints to the text sequence W. – Based on statistical N-gram language models 18

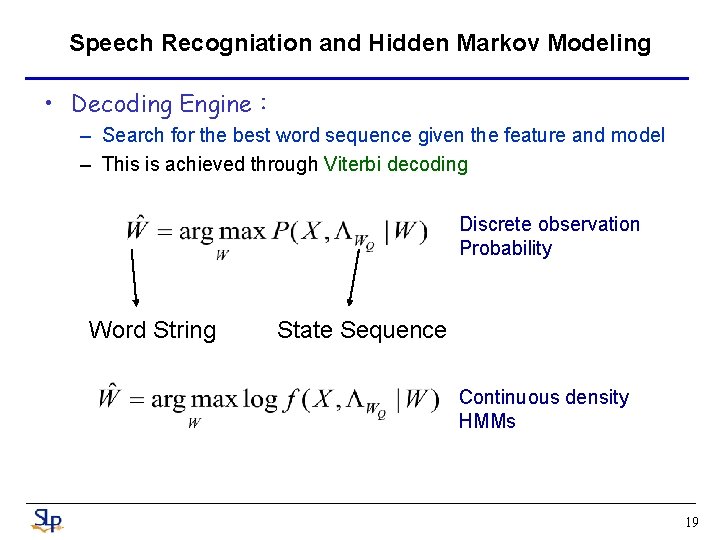
Speech Recogniation and Hidden Markov Modeling • Decoding Engine： – Search for the best word sequence given the feature and model – This is achieved through Viterbi decoding Discrete observation Probability Word String State Sequence Continuous density HMMs 19

Speech Recogniation and Hidden Markov Modeling • Hidden Markov modeling is a powerful statistical framework for time-varying quasi-stationary process and a popular choice for statistical modeling of speech signal 20

SPEECH RECOGNITION AND HIDDEN MARKOV MODELING • Three basic problems have to be resolved： • The evaluation problem – estimate the probability • The decoding problem – find a best state sequence q • The estimation problem – estimate HMM parameters from a given set of training samples (ML based algorithms such as Baum-Welch al. ) 21

MCE Classifier Design Using Discriminant Functions (19) MCE classifier design based on 3 steps 22

MCE Classifier Design Using Discriminant Functions • Misclassification measure (20) Generally we use 23

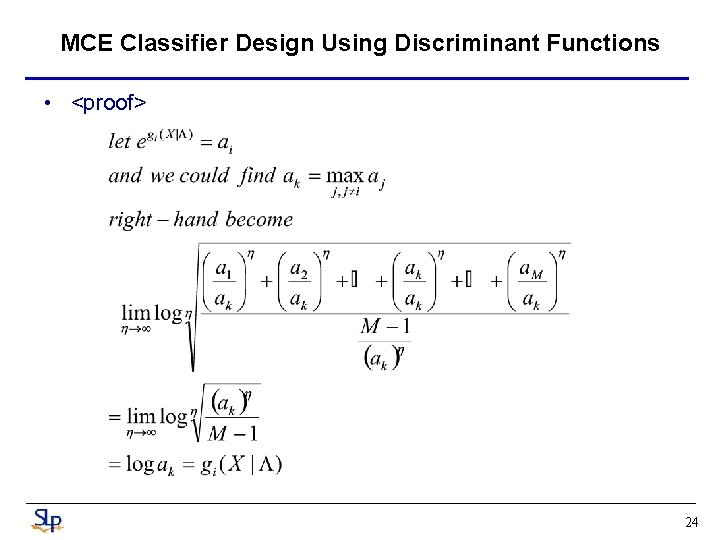
MCE Classifier Design Using Discriminant Functions • <proof> 24

MCE Classifier Design Using Discriminant Functions • Loss function (21) (22) 25

MCE Classifier Design Using Discriminant Functions • Classifier Performance Measure (23) (24) 26

MCE Classifier Design Using Discriminant Functions If posterior probability is used Then the Bayes’ minimum risk is (25) ? X 在 Class k 的機率不可最大，也就是說分錯的 loss 27

MCE Classifier Design Using Discriminant Functions If posterior probability is used Then the Bayes’ minimum risk is (26) 28

Optimization Methods • Expected Loss (27) We use GPD-based minimization algorithm to minimize it (28) Ut is the learning bias matrix to impose a different learning rate for the correct model vs. competing models 29

Optimization Methods 若滿足下面三個properties，則 收斂 30

Optimization Methods • Empirical Loss (31) If the training samples are obtained by an independent sampling from a space with a fixed probability distribution P (32) 31

HMM as a Discriminant Function 使用HMM當作discriminant function (34) discriminant function利用 有三種方式來產生 (35) (36) (37) 32

HMM as a Discriminant Function 33

HMM as a Discriminant Function 假設 Maintain HMM 原有的constraints 34

HMM as a Discriminant Function 所以我們使用parameter transformation來保留這些 constraints 35

HMM as a Discriminant Function , discriminant adjustment of the mean vector 36

HMM as a Discriminant Function 37

HMM as a Discriminant Function 38

HMM as a Discriminant Function , discriminant adjustment of the variance 39

HMM as a Discriminant Function 40

HMM as a Discriminant Function discriminant adjustment of the mixture weight 41

HMM as a Discriminant Function 42

HMM as a Discriminant Function • How to design the step size? – If the step size is too large, the classifier will be degraded at the start and sequential learning cannot be made successful – If the step size is too small, the convergence speed of the algorithm is too slow and it is practically not useful • It’s difficult to design it, the general solution is still lacking 43

HMM as a Discriminant Function • Why we normalize mean vector? – The magnitude of variances can vary in the range between 100 and 10 -5. – If using a constant step size for all mean vectors, the algorithm will either not converge or will be too slow to become practically useless • This takes away the dependencies on the variance variations 44

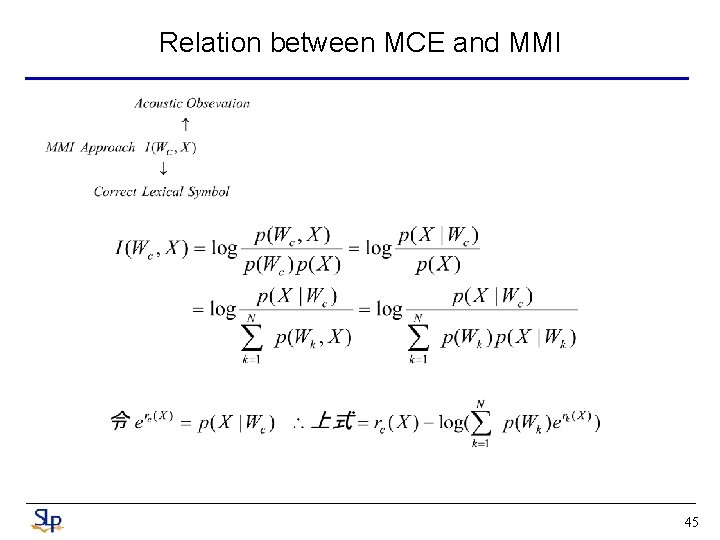
Relation between MCE and MMI 45

Relation between MCE and MMI 46

Relation between MCE and MMI 47

Relation between MCE and MMI 48

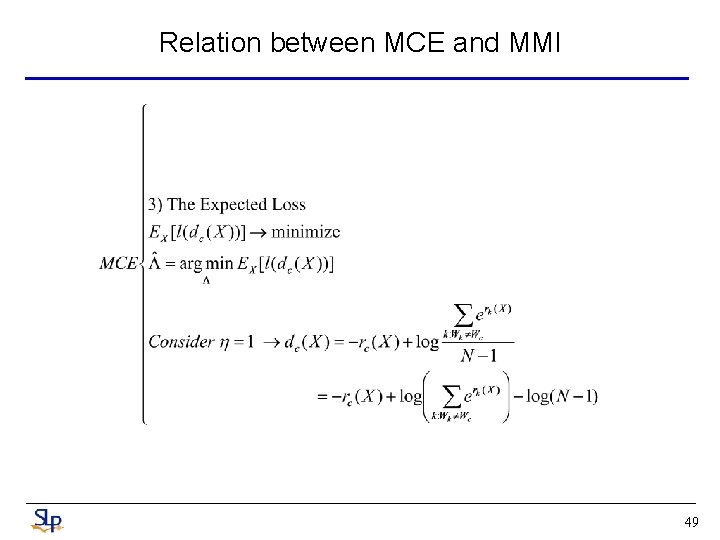
Relation between MCE and MMI 49

Relation between MCE and MMI 50

Relation between MCE and MMI The objective function in MMI is not bounded for dc(x)>0 This behavior may have some adverse effects in MMI based parameter estimation, since it is based on the mutual information I(Wc, X) averaged over the entire training set 51

Relation between MCE and MMI • MCE approach has several advantages in classifier design: – It is meaningful in the sense of minimizing the empirical recognition error rate of the classifier – If the true class posterior distributions are used as discriminant functions, the asymptotic behavior of the classifier will approximate the minimum Baye’s risk 52

SUMMARY • We examined the classical Bayes’ decision theory approach to the problem of pattern classification. • We don’t know the actual probability distribution • So we minimize the expected loss. Get a set of parameters. • Understand what MCE is, and how to use it to solve problems 53