Minimizing general submodular functions CVPR 2015 Tutorial Stefanie

Minimizing general submodular functions CVPR 2015 Tutorial Stefanie Jegelka MIT

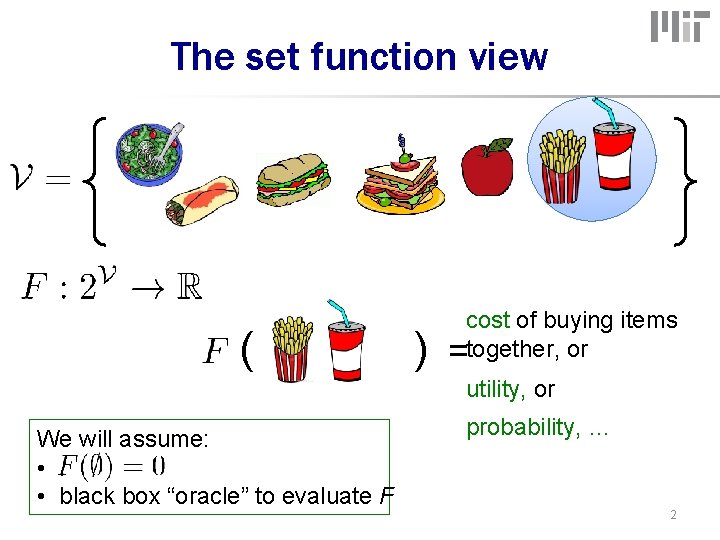
The set function view ( ) cost of buying items =together, or utility, or We will assume: • black box “oracle” to evaluate F probability, … 2

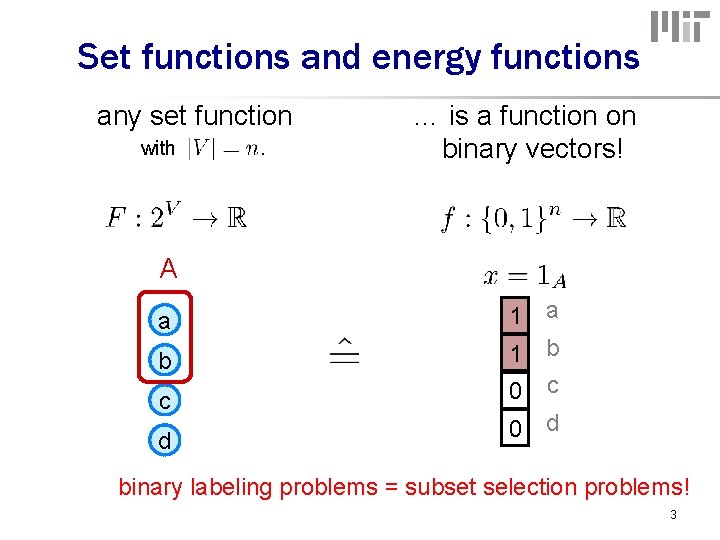
Set functions and energy functions any set function with . … is a function on binary vectors! A a a 1 b 0 c c d 0 d binary labeling problems = subset selection problems! 3

Discrete Labeling sky tree house grass 4

Summarization 5

Influential subsets

Submodularity extra cost: one drink extra cost: free refill diminishing marginal costs 7

The big picture graph theory (Frank 1993) G. Choquet game theory (Shapley 1970) submodular functions matroid theory (Whitney, 1935) stochastic processes (Macchi 1975, Borodin 2009) L. S. Shapley electrical networks (Narayanan 1997) J. Edmonds combinatorial optimization computer vision & machine learning L. Lovász

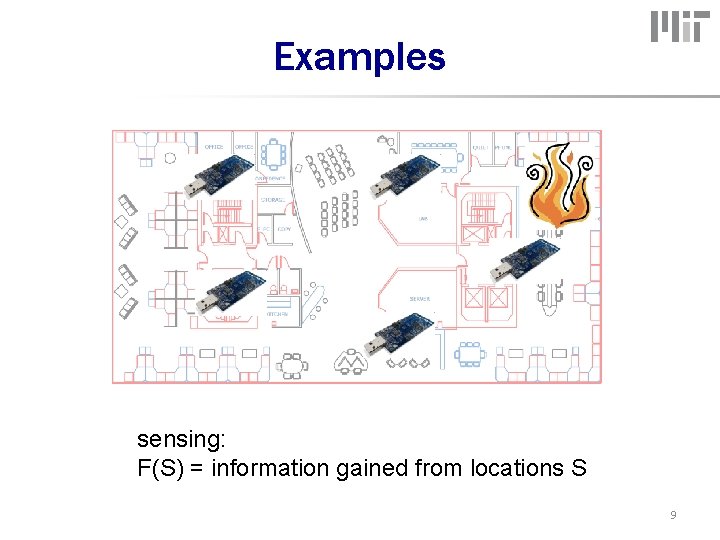
Examples sensing: F(S) = information gained from locations S 9

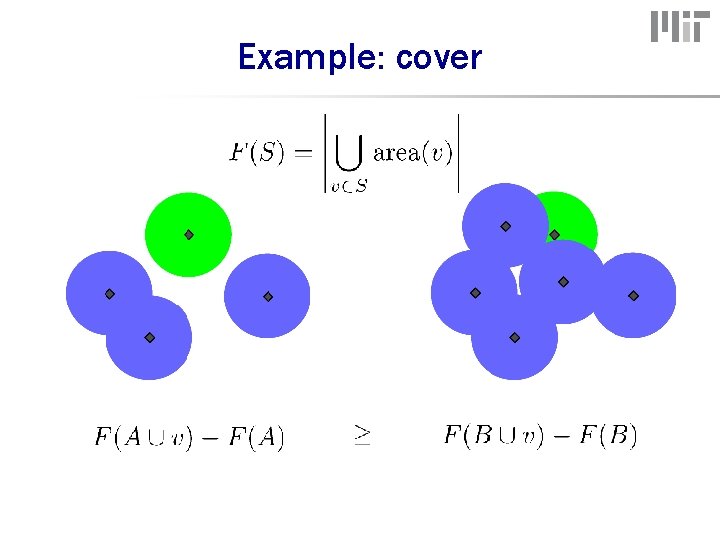
Example: cover

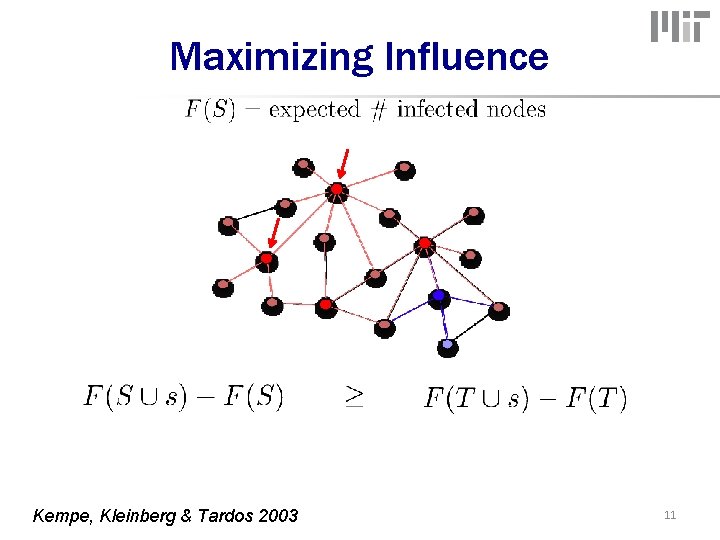
Maximizing Influence Kempe, Kleinberg & Tardos 2003 11

Submodular set functions • Diminishing gains: for all A + e • Union-Intersection: for all B + e

Submodularity: boolean & sets

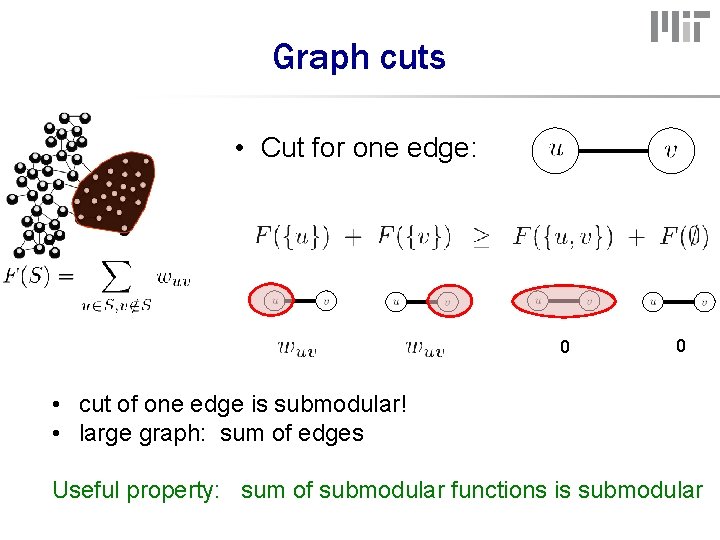
Graph cuts • Cut for one edge: 0 0 • cut of one edge is submodular! • large graph: sum of edges Useful property: sum of submodular functions is submodular

Other closedness properties submodular on . The following are submodular: • Restriction: VV SS W 15

Other closedness properties submodular on . The following are submodular: • Restriction: • Conditioning: VV SS W 16

Closedness properties submodular on . The following are submodular: • Restriction: • Conditioning: • Reflection: V S 17

Submodular optimization • subset selection: min / max F(S) • minimizing submodular functions: next • maximizing submodular functions: afternoon convex … … and concave aspects!

Minimizing submodular functions Why? • energy minimization • variational inference (marginals) • structured sparse estimation … How? • graph cuts – fast, not always possible • convex relaxations – can be fast, always possible • …

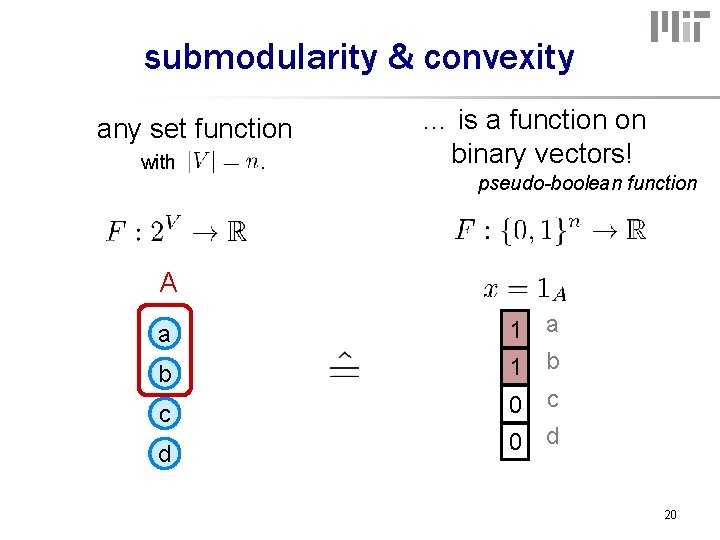
submodularity & convexity any set function with . … is a function on binary vectors! pseudo-boolean function A a a 1 b 0 c c d 0 d 20

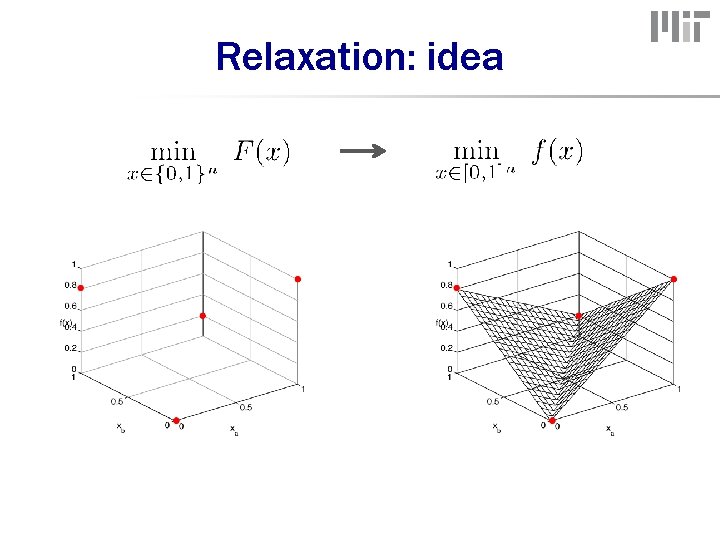
Relaxation: idea

A relaxation (extension) have (1. 0 - 0. 5) want: extension + (0. 5 – 0. 2) + (0. 2)

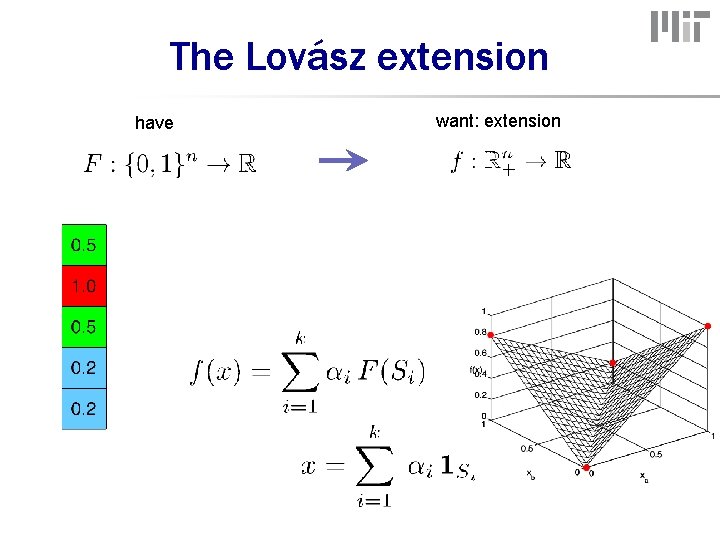
The Lovász extension have want: extension

Examples • truncation 1. 0 - 0. 5 • cut function “total variation”!

Alternative characterization if F is submodular, this is equivalent to: Theorem (Lovász, 1983) Lovasz extension is convex F is submodular.

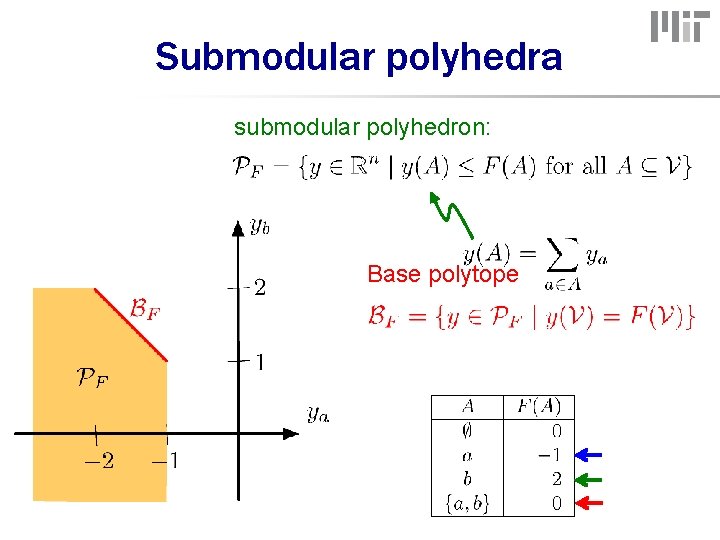
Submodular polyhedra submodular polyhedron: Base polytope

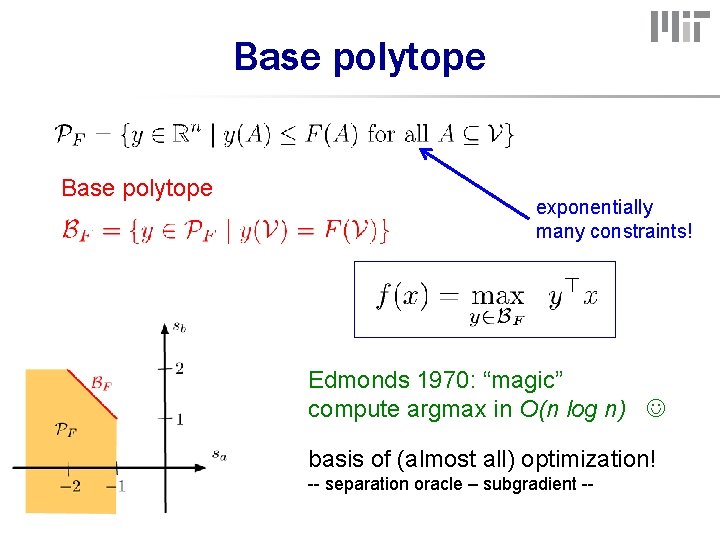
Base polytope exponentially many constraints! Edmonds 1970: “magic” compute argmax in O(n log n) basis of (almost all) optimization! -- separation oracle – subgradient --

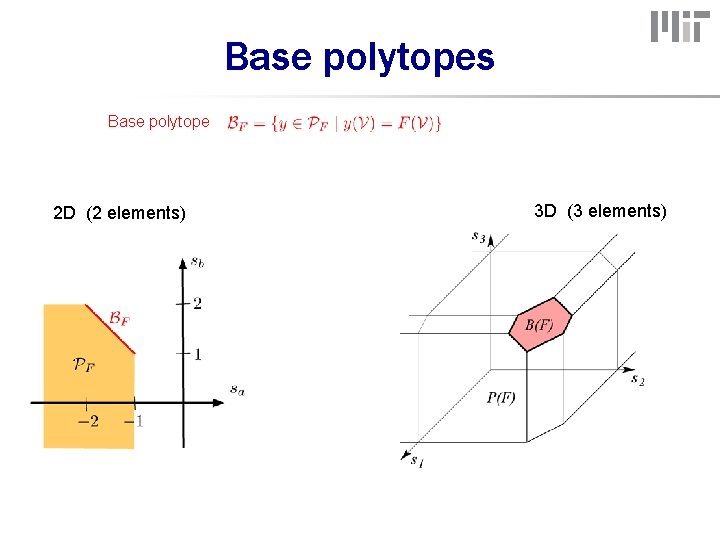
Base polytopes Base polytope 2 D (2 elements) 3 D (3 elements)

Convex relaxation 1. relaxation: convex optimization (non-smooth) 2. relaxation is exact! submodular minimization in polynomial time! (Grötschel, Lovász, Schrijver 1981)

Submodular minimization • minimize – subgradient descent – smoothing (special cases) • solve dual: combinatorial algorithms – foundations: Edmonds, Cunningham – first poly-time algorithms: (Iwata-Fujishige-Fleischer 2001, Schrijver 2000) – many more after that …

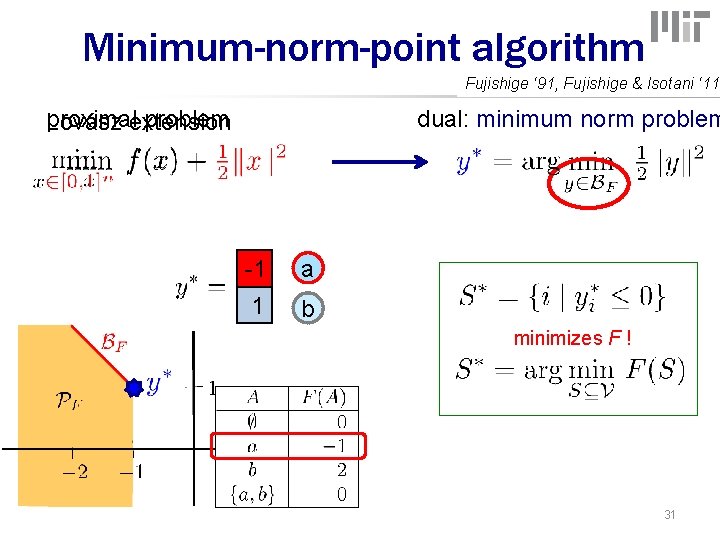
Minimum-norm-point algorithm Fujishige ‘ 91, Fujishige & Isotani ‘ 11 dual: minimum norm problem proximal problem Lovász extension -1 a 1 b minimizes F ! 31

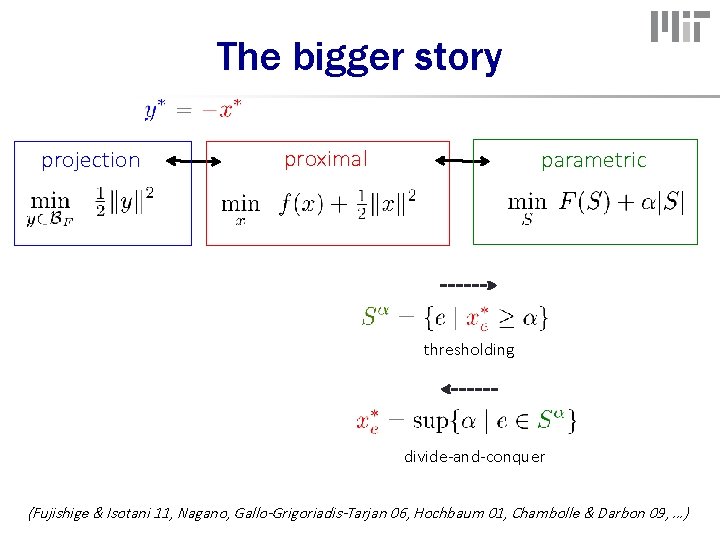
The bigger story projection proximal parametric thresholding divide-and-conquer (Fujishige & Isotani 11, Nagano, Gallo-Grigoriadis-Tarjan 06, Hochbaum 01, Chambolle & Darbon 09, …)

Minimum-norm-point algorithm 1. optimization: find how solve? 2. rounding: Polytope -0. 5 a has exponentiallyamany inequalities / faces -0. 5 b BUT: can do linear optimizationbover c 0. 8 c Frank-Wolfe or Fujishige-Wolfe algorithm 1. 0 d d

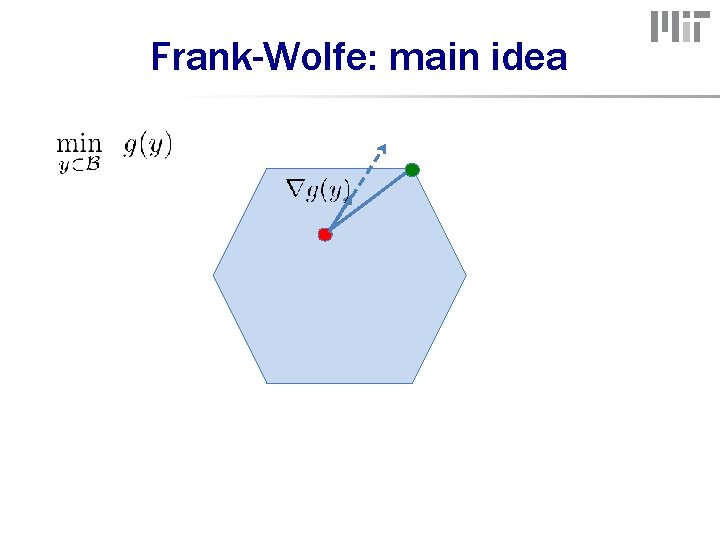
Frank-Wolfe: main idea

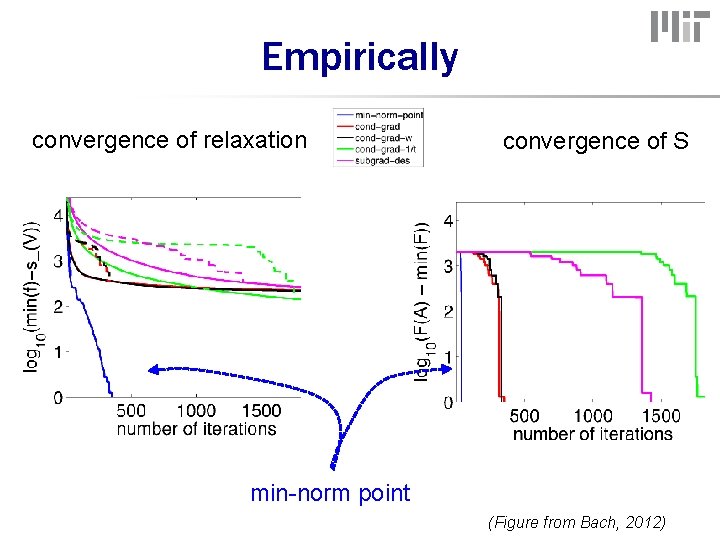
Empirically convergence of relaxation convergence of S min-norm point (Figure from Bach, 2012)

Recap – links to convexity • submodular function F(S) • convex extension f(x) --- can compute it! • submodular minimization as convex optimization -- can solve it! • What can we do with it?

Links to convexity • What can we do with it? • MAP inference / energy minimization (out-of-the-box) • variational inference (Djolonga & Krause 2014) • structured sparsity (Bach 2010) • decomposition & parallel algorithms

Structured sparsity and submodularity

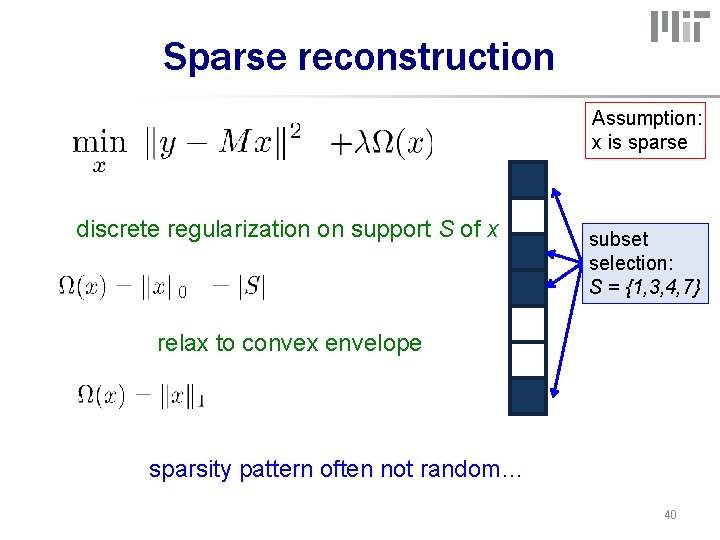
Sparse reconstruction Assumption: x is sparse discrete regularization on support S of x subset selection: S = {1, 3, 4, 7} relax to convex envelope sparsity pattern often not random… 40

Structured sparsity Assumption: support of x has structure express by set function!

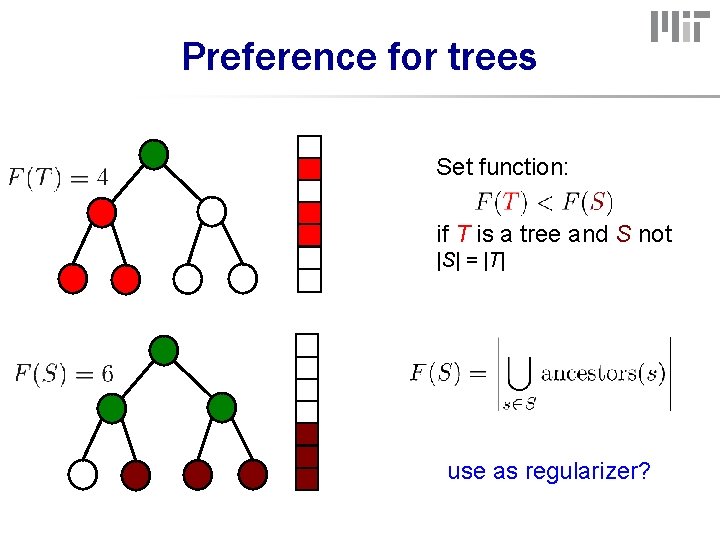
Preference for trees Set function: if T is a tree and S not |S| = |T| use as regularizer?

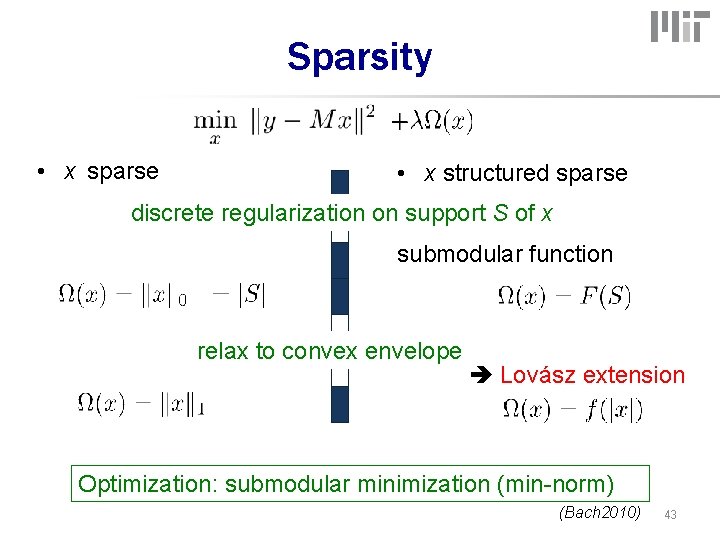
Sparsity • x sparse • x structured sparse discrete regularization on support S of x submodular function relax to convex envelope Lovász extension Optimization: submodular minimization (min-norm) (Bach 2010) 43

Special case • minimize a sum of submodular functions “easy” • combinatorial algorithms (Kolmogorov 12, Fix-Joachims-Park-Zabih 13, Fix-Wang-Zabih 14) • convex relaxations

Relaxation • convex Lovász extension: tight relaxation • dual decomposition: parallel algorithms (Komodakis-Paragios-Tziritas 11, Savchynskyy-Schmidt-Kappes-Schnörr 11, J-Bach-Sra 13)

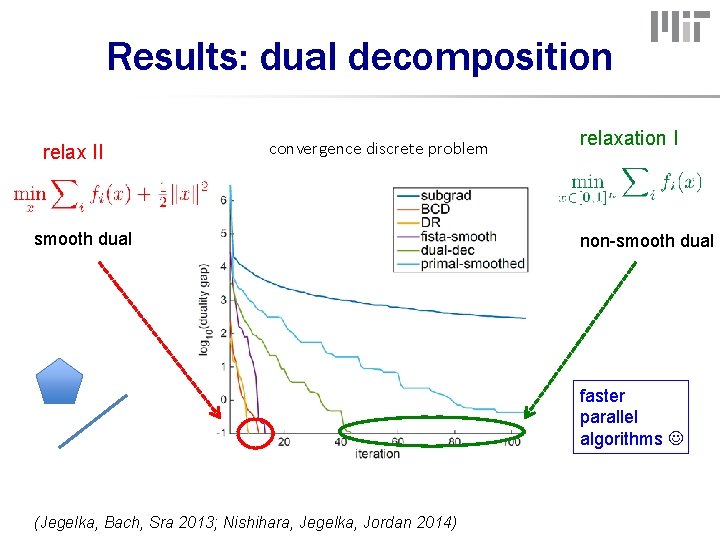
Results: dual decomposition relax II convergence discrete problem smooth dual relaxation I non-smooth dual faster parallel algorithms (Jegelka, Bach, Sra 2013; Nishihara, Jegelka, Jordan 2014)

Summary • Submodular functions – diminishing returns/costs • convex relations: – exact relaxation – structured norms – fast algorithms • more soon: – constraints – maximization: diversity, information