Minimizers Reducing Storage Requirements for Biological Sequence Comparison

Minimizers Reducing Storage Requirements for Biological Sequence Comparison M. Roberts et al, 2004 November 2018 Deep Sequencing Seminar Avia Efrat, Tomer Ronen

Previously On “Algorithms for Deep Sequencing” • Last Week: o Find identical parts between documents o Reduce the needed storage for the algorithm • Similarities to Last Week: o Comparing between documents o Large storage reduction, small performance hit • Differences from Last Week o Biology domain - our “documents” are sequences of nucleic acids (ACGT) and proteins. o Different options for choosing the “representative k-mers” o A bit on similarities, not just identical strings. 2

Problem • Given two long sequences, find common substrings (and their location) • “Common”: Not necessarily Identical, But “similar”. The similarity is a function of the differences between the two strings, and can be determined by the user. A C G T A A A G T C A G G T C Not Similar enough 3

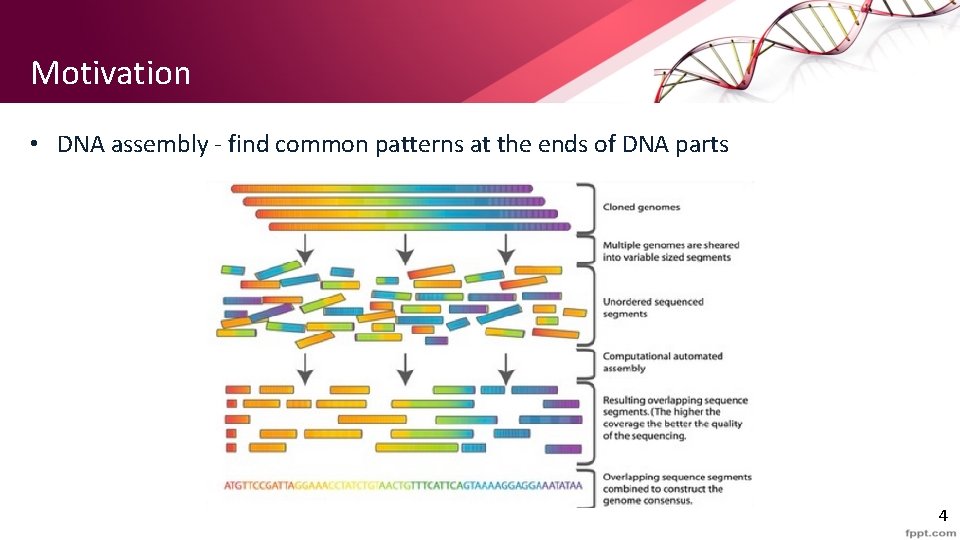
Motivation • DNA assembly - find common patterns at the ends of DNA parts 4

Motivation • Homology - similar parts may suggest common ancestry or similar “function”. 5

k-mers • k-mer: a substring of length k • In a string with length L, there are L-k+1 k-mers: 1 2 3 4 5 A C G G T Intuition: 1 2 3 A C G 2 3 4 C G G 3 4 5 G G T In the first L-k indices there are L-k k-mers. In the last k indices there is only place for 1 more k-mer. 6

“Seed and Extend” • We want to find common substrings between two strings. • What about more than two strings? And similarity? Later! • We get k-mers from both strings. These are the “seeds”. o How do we choose these seeds/k-mers? Good question! • Each seed is represented by 3 -tuple: <s, i, p> o s - the k-mer letters o i - the index of the string (in our case: ‘ 1’ or ‘ 2’) o p - the starting position of the k-mer in the string 7

Finding Common K-mers • Sort your list of k-mers (your “seeds”). • Now identical seeds are one after another, making it easy to find the corresponding strings and try to extend the seed matches. • The ability to recognize matches as soon as the database is sorted is called the “collection criterion”. 8

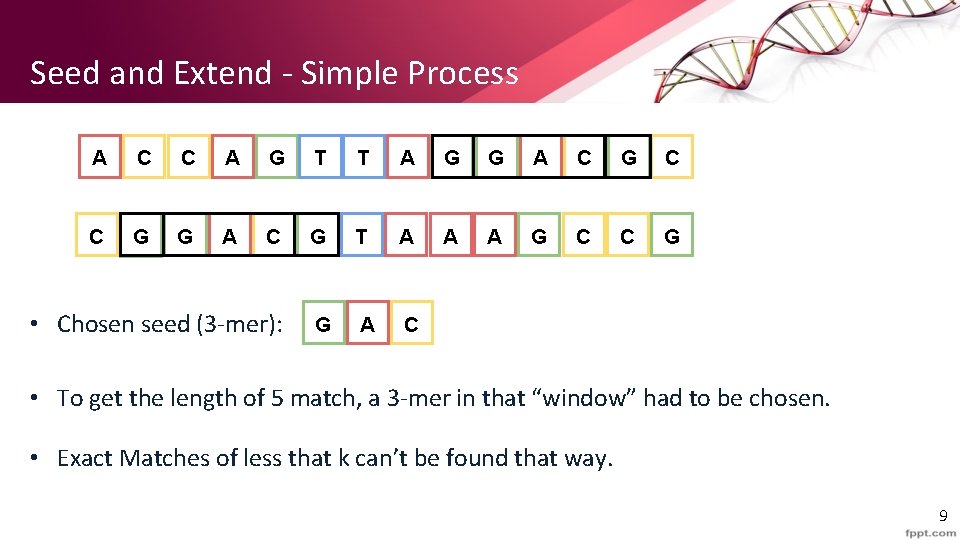
Seed and Extend - Simple Process A C C A G T T A G G A C G C C G G A C G T A A A G C C G • Chosen seed (3 -mer): G A C • To get the length of 5 match, a 3 -mer in that “window” had to be chosen. • Exact Matches of less that k can’t be found that way. 9

Storage Cost: Naïve Choice of K-Mers • 10

Reducing Storage Requirements • 11

Minimizers • Minimizers: a special set of representative k-mers. • The Representation Property (Property 1): o If two strings have a significant exact match, then at least one of the minimizers chosen from one will also be chosen from the other. 12

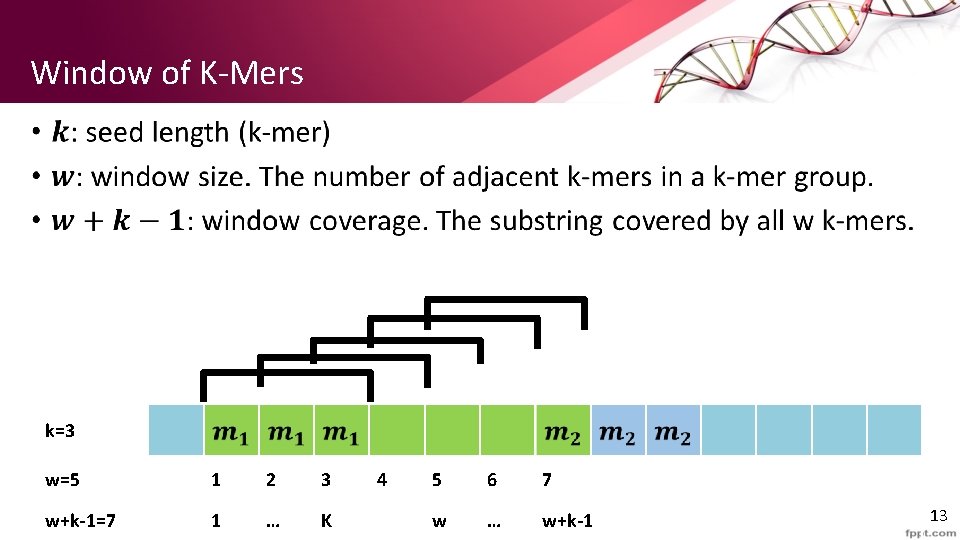
Window of K-Mers • k=3 w=5 1 2 3 w+k-1=7 1 … K 4 5 6 7 w … w+k-1 13

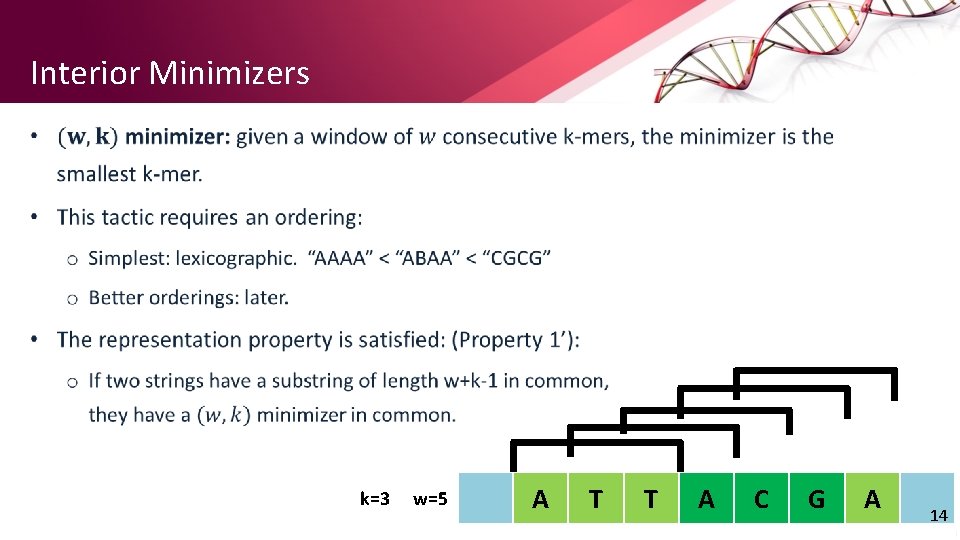
Interior Minimizers • k=3 w=5 A T T A C G A 14

Interior Minimizers • 15

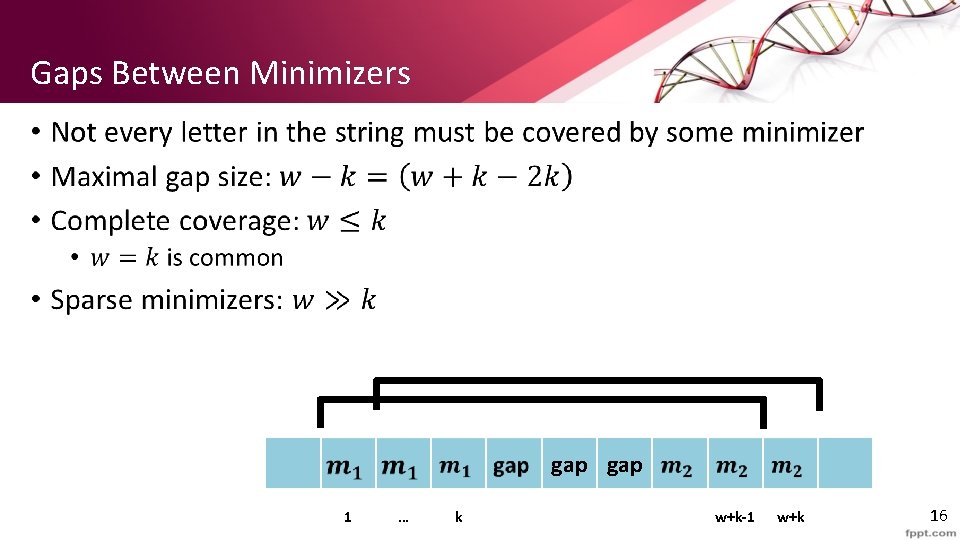
Gaps Between Minimizers • gap 1 … k w+k-1 w+k 16

End Minimizers • 17

End Minimizers • 18

Mixed Strategy • 19

Ordering - Effect on Storage • 20

Ordering - Effect on Storage • 21

Ordering Effect on Match Significance • Ordering by “rarity” does not only help in reducing storage • We want our matches to be significant. • If we want to see if two articles are similar, The word “protein” in both of them is more indicative of a resemblance than multiple co-occurrences of the phrase “this is a“. • Same with genes - a match of CGCG is more significant than a match of AAAA. The order can impact both storage requirements and the statistical significance of the matches that were found. The latter is important when minimizers are sparse (not covering the whole string). 22

A Bit on Similarity • • Like matches, not all mismatches are the same. BLAST: a family of algorithms for sequence matching. o Seed & Extend: Start from seeds, tries to extend from there. o Can look for similarities, not just exact matches. o Similarities are determined by a similarity score matrix. 23

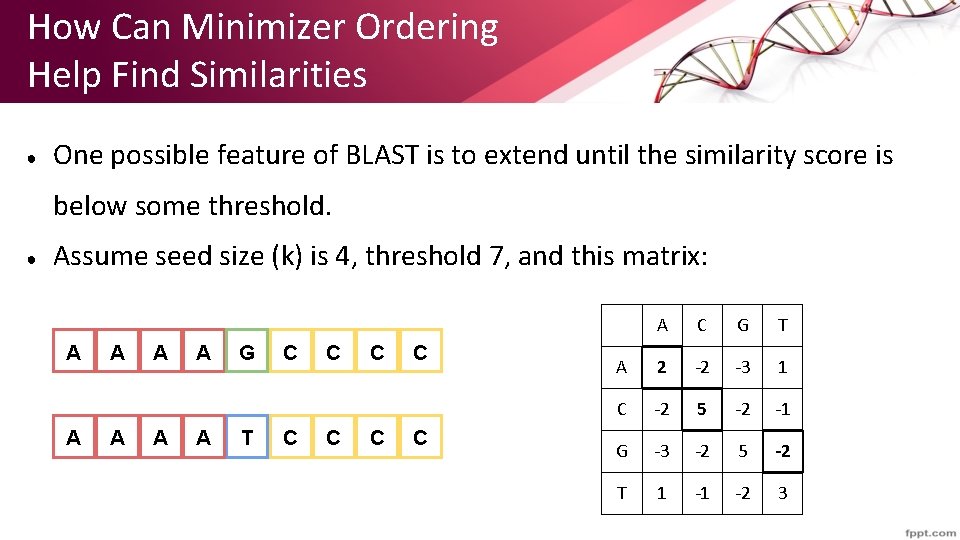
How Can Minimizer Ordering Help Find Similarities ● One possible feature of BLAST is to extend until the similarity score is below some threshold. ● Assume seed size (k) is 4, threshold 7, and this matrix: A A A A G T C C C C A C G T A 2 -2 -3 1 C -2 5 -2 -1 G -3 -2 5 -2 T 1 -1 -2 3

Case Study • 25

Case Study • 26

Case Study • 27

Symmetrizer • A technique for finding missing overlaps • If read X plausibly overlaps reads Y and Z, and the offsets suggest that Y and Z overlap, then Y and Z are sent to the Extender part of the algorithm. • In the example: the overlap between R and B is insufficient to reliably produce a minimizer, but their offsets relative to G suggest that they do in fact overlap. 28

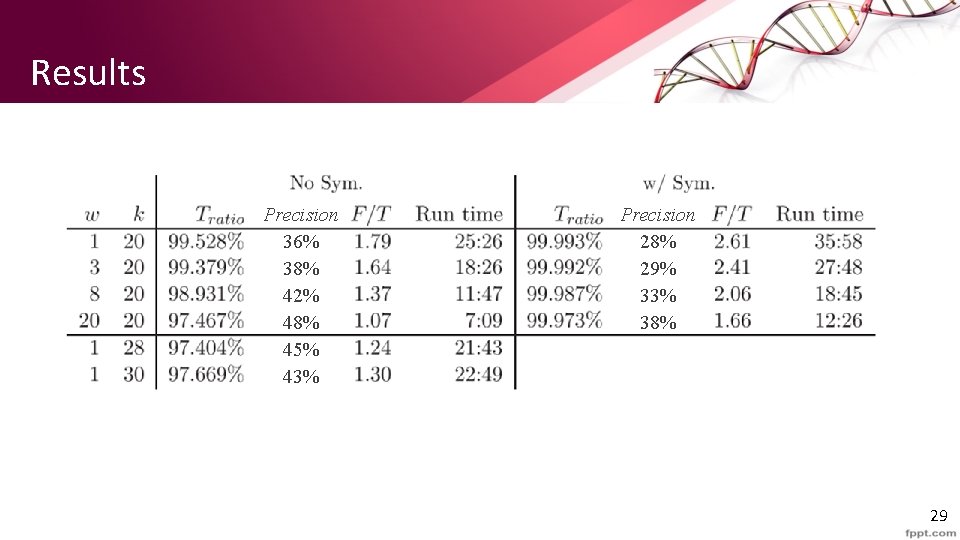
Results Precision 36% 38% 42% 48% 45% 43% Precision 28% 29% 33% 38% 29

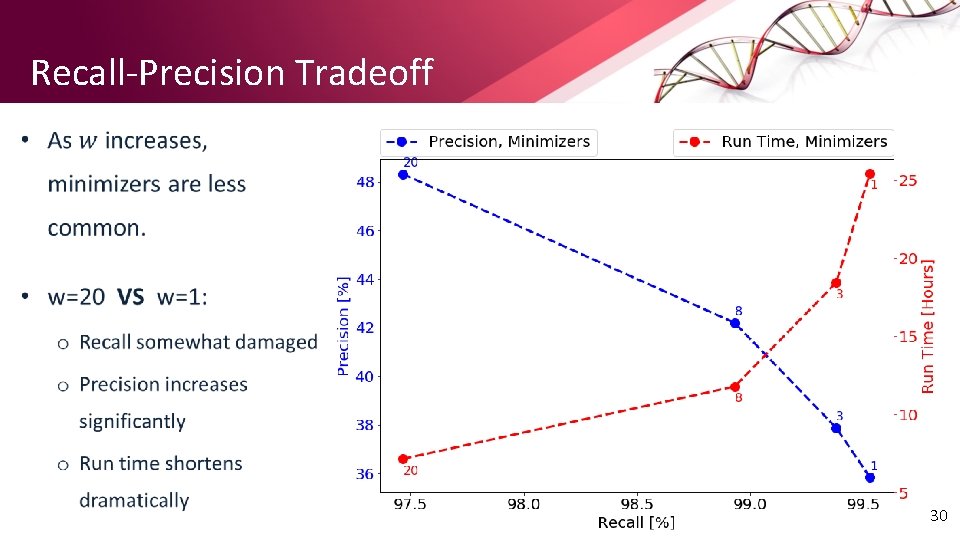
Recall-Precision Tradeoff • 30

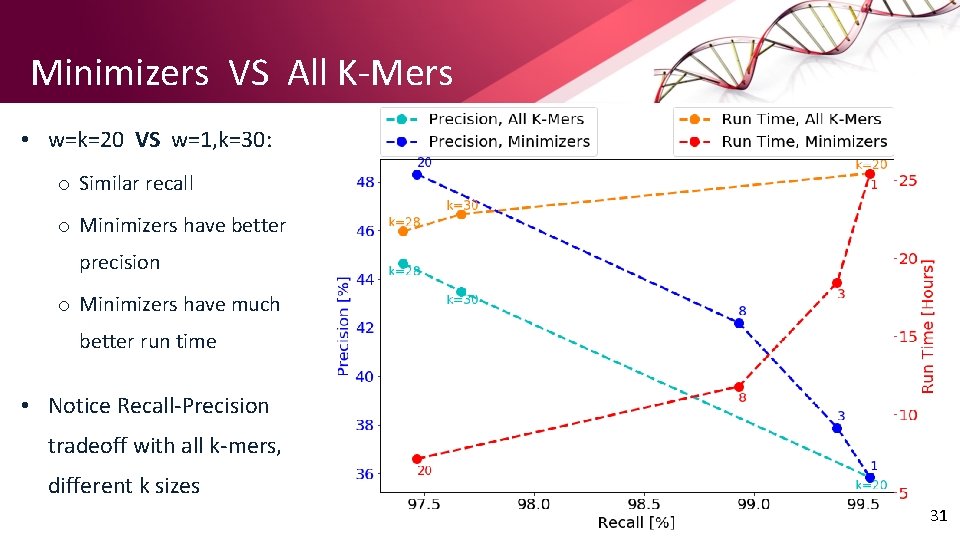
Minimizers VS All K-Mers • w=k=20 VS w=1, k=30: o Similar recall o Minimizers have better precision o Minimizers have much better run time • Notice Recall-Precision tradeoff with all k-mers, different k sizes 31

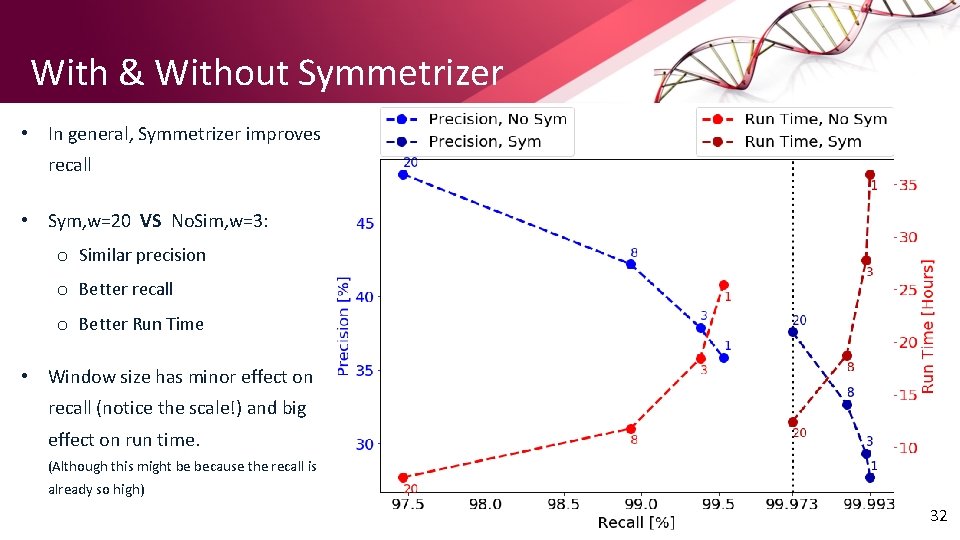
With & Without Symmetrizer • In general, Symmetrizer improves recall • Sym, w=20 VS No. Sim, w=3: o Similar precision o Better recall o Better Run Time • Window size has minor effect on recall (notice the scale!) and big effect on run time. (Although this might be because the recall is already so high) 32

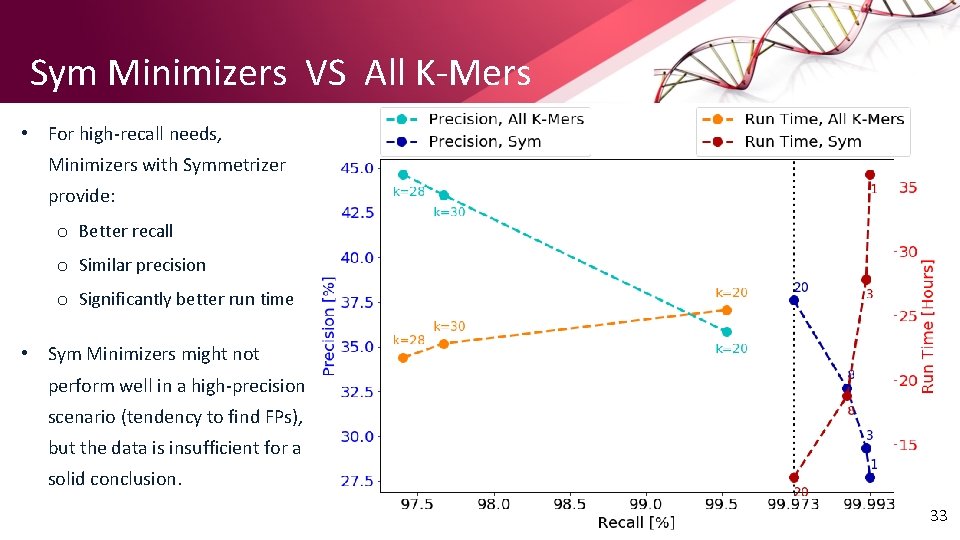
Sym Minimizers VS All K-Mers • For high-recall needs, Minimizers with Symmetrizer provide: o Better recall o Similar precision o Significantly better run time • Sym Minimizers might not perform well in a high-precision scenario (tendency to find FPs), but the data is insufficient for a solid conclusion. 33

Recall Equivalence • 34

Minimizers vs. All k-mers: Precision • 35

Looking for Long Matches? Minimizers! • 36

What About shorter Matches? • 37

Summary • 38