Mini Project in Implementing Parallel Graph Algorithms Hits

Mini Project in Implementing Parallel Graph Algorithms Hits Algorithm Edward Erlich, Tair Hakman

Background • Hyperlink-Induced Topic Search (HITS for short) is a form of page ranking algorithm. • It takes n most relevant pages for a certain search (by key word, for example) and create a graph in which each node represents a page and has two fields – Hubs, Authority. • Hubs - how many pages a certain page directs to • Authority (auth for short) – how many pages points to a certain page.

The Hits Algorithm Computation • The algorithm is defined by two main loops: • Authority Update – update each node’s Auth to be the sum of the Hubs score of its incoming neighbors. • Hubs Update - update each node’s Hubs to be the sum of the Auth score of its outgoing neighbors.

Algorithm Computation(cont) The following Algorithm is applied: 1. Start with each node having a hub score and authority score of 1. 2. Run the Authority Update Rule on all nodes. 3. Run the Hub Update Rule on all nodes. 4. Normalize the values by dividing each Hub score by square root of the sum of the squares of all Hub scores, and dividing each Authority score by square root of the sum of the squares of all Authority scores. 5. Repeat from the second step as necessary.

Psuedo Code

Converting the Algorithm • As required , we had to convert out Algorithm, and create an Operator Formulation of it.

Operator Formulation

Pre – Implementation Observations • Each operation inside 'Operator Formulation' doesn't required a guard in it's form. • The algorithm does not changes the structure of the graph (the sets of nodes and edges) and therefore we should pick a graph data structure geared towards computations that do not change its structure. • The 'init' loop applies the 'init. Auth. Hub' operator to nodes such that their activities do not interfere. Therefore no synchronization is required. • The 'hits' parallel loop has an init stage which applies an operator to nodes such that their activities do not interfere. Therefore no synchronization is required. • The 'hits' parallel loop has a update stage which applies an operator to nodes such that their activities may interfere. Therefore synchronization is required. • relax. Hub operator only applies on outgoing neighbors and the relax. Auth operator only applies on the incoming neighbors.

Serial Implementation • We Implemented the previously shown Algorithm using In-out graph. • There was a need to differ incoming neighbors from outgoing neighbors thus the Graph selection. • Our Algorithm was based on 6 loops, 3 for updating the hubs and 3 for updating the authority. • We added to the Galois Graph node two fields – Hubs and Auth.

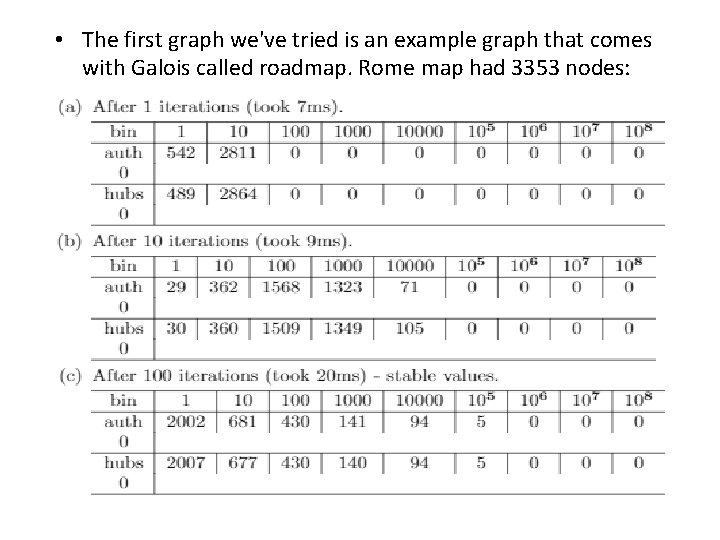
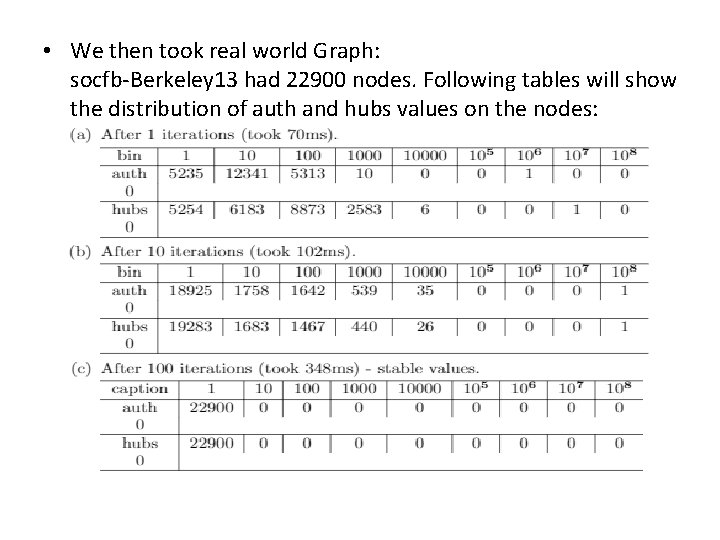
Experimental Evaluation • The tables below describes the distribution of Auth and Hubs values on the nodes, where bin is the count of values of a specific property(for ex. In the first table, "542" is the number of vertexes who’s auth value is between 1 and 10)

• The first graph we've tried is an example graph that comes with Galois called roadmap. Rome map had 3353 nodes:

• We then took real world Graph: socfb-Berkeley 13 had 22900 nodes. Following tables will show the distribution of auth and hubs values on the nodes:

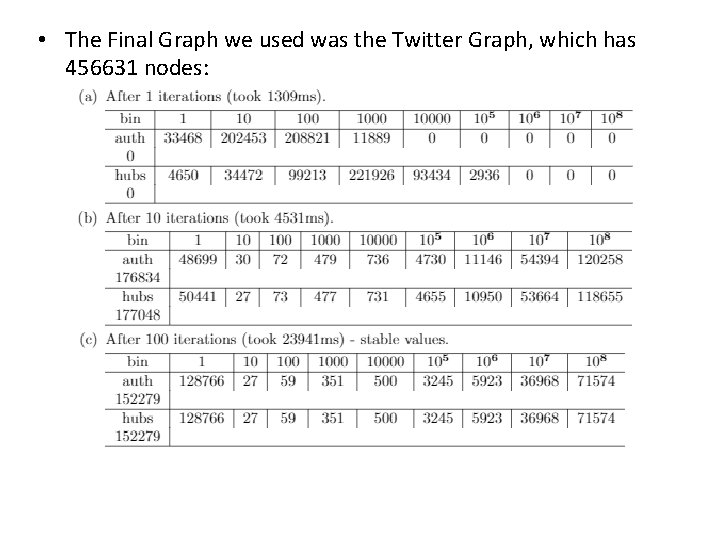
• The Final Graph we used was the Twitter Graph, which has 456631 nodes:

Parallel Implementation • We implemented the previously shown pseudo-code using inline-edge graph. • Our Algorithm is based on 2 loops, one for Auth and one for Hubs. • We added a size 2 array for Hubs and a size 2 array for Auth, in order to save both pre and post update values, so the threads won’t interfere with each other’s work.

Experimental Evaluation • We computed a test: running 100 iterations on a graph for several times where each time will have a different number of threads. • The graphs in the following slides will show our results running n threads.

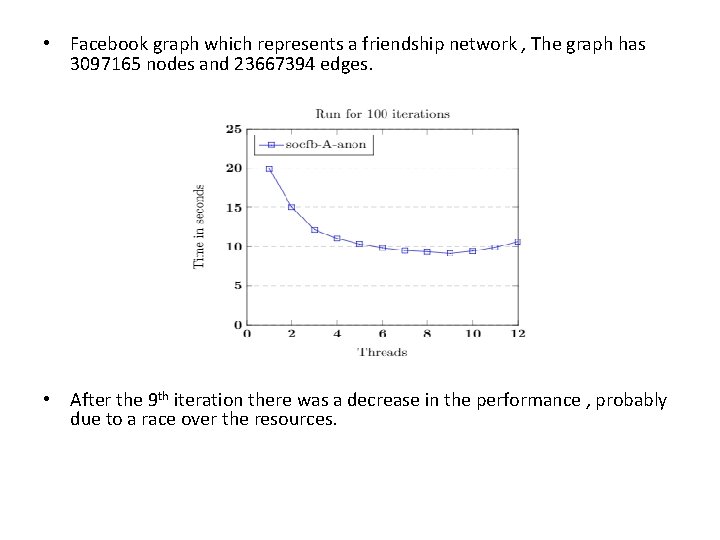
• Facebook graph which represents a friendship network , The graph has 3097165 nodes and 23667394 edges. • After the 9 th iteration there was a decrease in the performance , probably due to a race over the resources.

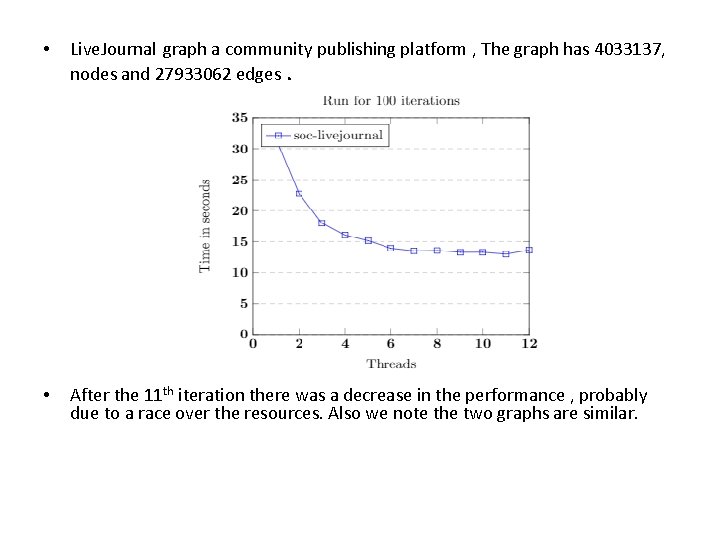
• Live. Journal graph a community publishing platform , The graph has 4033137, nodes and 27933062 edges. • After the 11 th iteration there was a decrease in the performance , probably due to a race over the resources. Also we note the two graphs are similar.

Final Conclusions • We can see that the parallel Algorithm improves the results tremendously. • After a certain amount of Threads, we can also note that the improvement stabilize around a certain value (differ based on graph).