MIMO MULTIUSER schemes for downlink transmissions theoretic bounds

MIMO MULTIUSER schemes for downlink transmissions: theoretic bounds and practical techniques Federico Boccardi Bell Laboratories Paris, 29/3/2007 (joint work with Howard Huang)

Outline - An introduction to SDMA techniques. - The capacity region of the MIMO-BC and the optimal DPC scheme. - Suboptimal schemes, the single receive antenna case. - Extension to multiple receive antennas. - Imperfect channel state information at the transmitter side. 2 All Rights Reserved © Alcatel-Lucent 2006

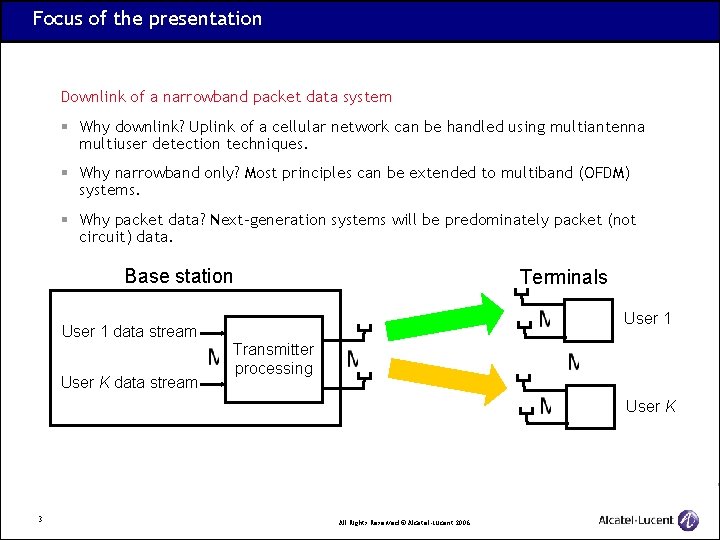
Focus of the presentation Downlink of a narrowband packet data system § Why downlink? Uplink of a cellular network can be handled using multiantenna multiuser detection techniques. § Why narrowband only? Most principles can be extended to multiband (OFDM) systems. § Why packet data? Next-generation systems will be predominately packet (not circuit) data. Base station Terminals User 1 data stream User K data stream Transmitter processing User K 3 All Rights Reserved © Alcatel-Lucent 2006

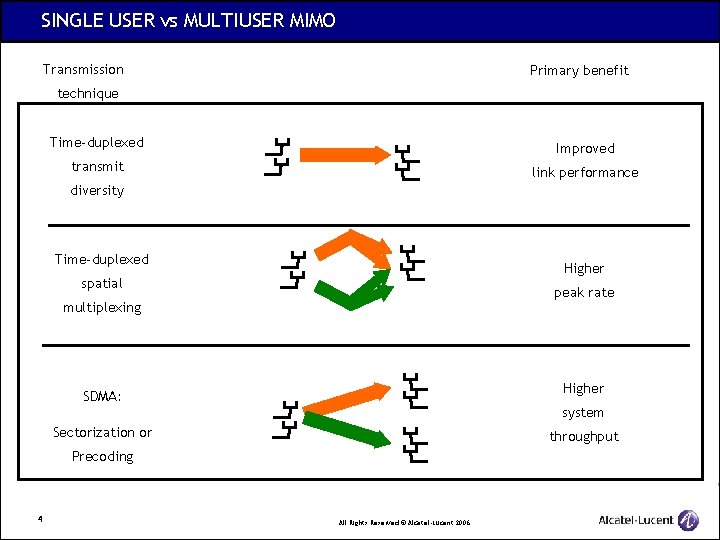
SINGLE USER vs MULTIUSER MIMO Transmission Primary benefit technique Time-duplexed Improved transmit link performance diversity Time-duplexed Higher spatial peak rate multiplexing Higher SDMA: system Sectorization or throughput Precoding 4 All Rights Reserved © Alcatel-Lucent 2006

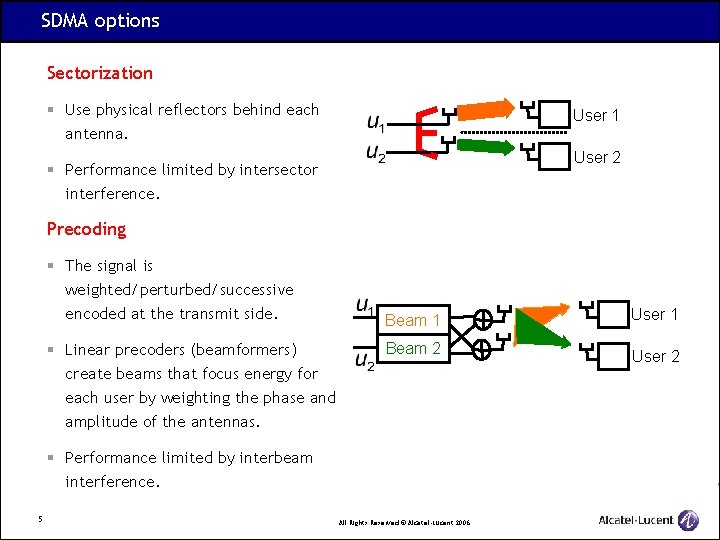
SDMA options Sectorization § Use physical reflectors behind each antenna. User 1 User 2 § Performance limited by intersector interference. Precoding § The signal is weighted/perturbed/successive encoded at the transmit side. § Linear precoders (beamformers) create beams that focus energy for each user by weighting the phase and amplitude of the antennas. Beam 1 User 1 Beam 2 User 2 § Performance limited by interbeam interference. 5 All Rights Reserved © Alcatel-Lucent 2006

System model § A narrowband MIMO downlink with M antennas at the transmitter and K receivers with N antennas each can be modelled as MIMO Gaussian broadcast channel. § The received signal for the kth user is given by § Under a sum-power constraint (SPC) the transmit signal is subject to the following constraint § Under a per-antenna-power constraint (PAPC) the transmit signal is subject to the following constraint 6 All Rights Reserved © Alcatel-Lucent 2006

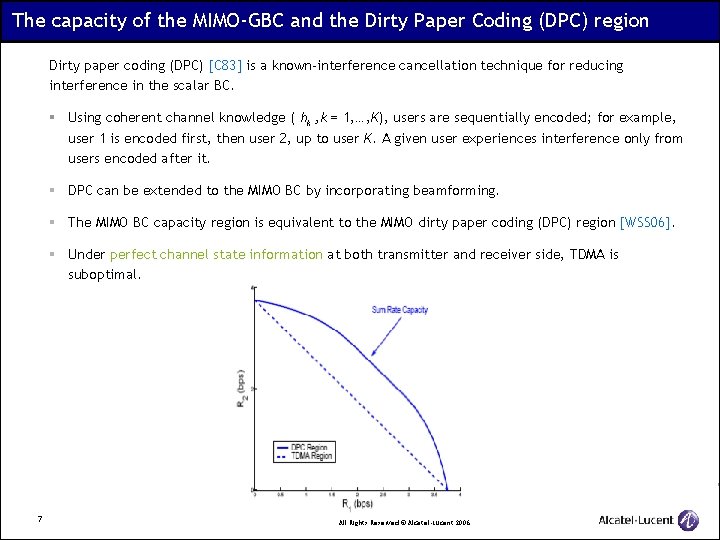
The capacity of the MIMO-GBC and the Dirty Paper Coding (DPC) region Dirty paper coding (DPC) [C 83] is a known-interference cancellation technique for reducing interference in the scalar BC. § Using coherent channel knowledge ( hk , k = 1, …, K), users are sequentially encoded; for example, user 1 is encoded first, then user 2, up to user K. A given user experiences interference only from users encoded after it. § DPC can be extended to the MIMO BC by incorporating beamforming. § The MIMO BC capacity region is equivalent to the MIMO dirty paper coding (DPC) region [WSS 06]. § Under perfect channel state information at both transmitter and receiver side, TDMA is suboptimal. 7 All Rights Reserved © Alcatel-Lucent 2006

Suboptimal linear and non-linear precoding schemes § Linear precoding General expression: where S is the subset of users for a given channel realization. § Non linear precoding - Vector Precoding (VP): A data-dependent perturbation vector is used after the linear precoding stage - Tomlinson-Harashima and QR decomposition: Part of the interference is eliminated by using a QR decomposition of the channel; the other part is eliminate by using the Tomlinson-Harashima precoder for each subchannel. For the k-th streams: 8 All Rights Reserved © Alcatel-Lucent 2006

Linear precoding Sectorization via fixed beamforming § Fixed beams + correlated antennas. § Create virtual sectors using fixed beams. § Turn on all beams simultaneously for increased throughput. § Turn on beams individually for increased range and coverage. [SH 04] User dependent beamforming § User-specific beams + uncorrelated antennas. § Transmitter uses CSI to form simultaneous beams to multiple users. Beams are designed so that, under ideal CSI knowledge, users receive no interbeam interference. § Can be shown to achieve optimum asymptotic capacity scaling. [YG 06] 9 All Rights Reserved © Alcatel-Lucent 2006

ZF linear precoding with user selection § For a fixed subset of users the general ZF with per-antenna power constraint problem can be formulated as scheduling coefficients beamforming coefficients power allocation § This is a convex constrained optimization problem and in general can be solved by using an interior point method. For the particular case of sum-power constraint the optimum power allocation is given by the so-called waterfilling power allocation. § An external optimization has to be used for the choice of the transmitting user subset § The optimal solution requires a brute force search over all possible sets S of users. A practical greedy algorithm can be used. [YG 06, BH 06] 10 All Rights Reserved © Alcatel-Lucent 2006

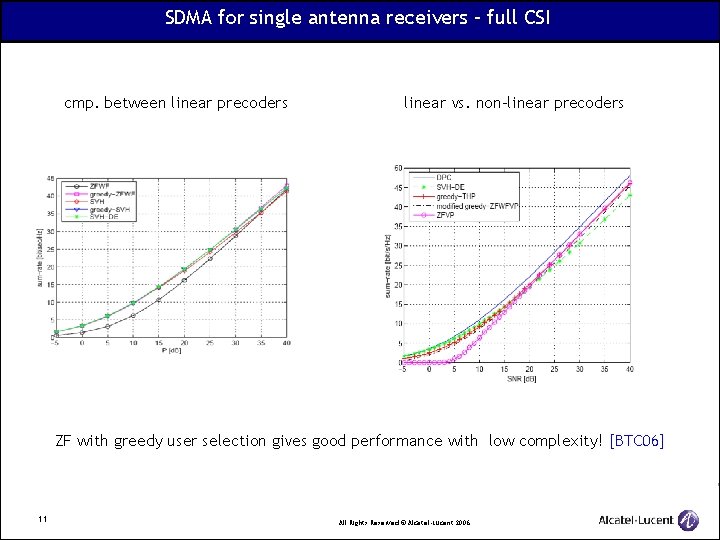
SDMA for single antenna receivers – full CSI cmp. between linear precoders linear vs. non-linear precoders ZF with greedy user selection gives good performance with low complexity! [BTC 06] 11 All Rights Reserved © Alcatel-Lucent 2006

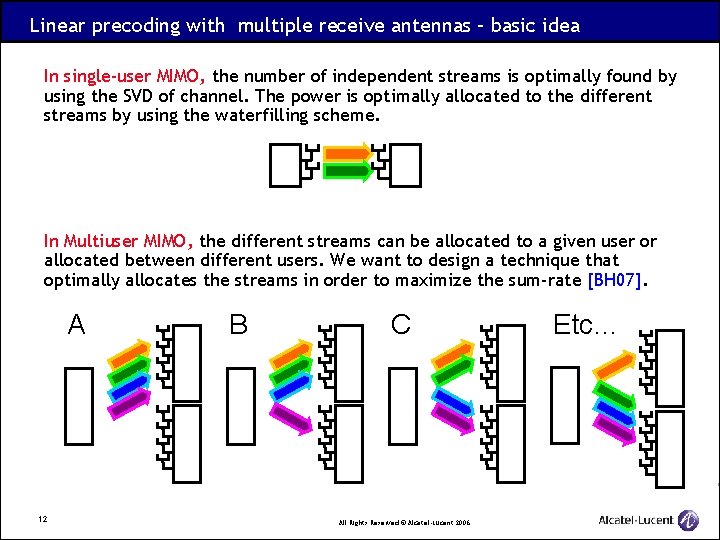
Linear precoding with multiple receive antennas – basic idea In single-user MIMO, the number of independent streams is optimally found by using the SVD of channel. The power is optimally allocated to the different streams by using the waterfilling scheme. In Multiuser MIMO, the different streams can be allocated to a given user or allocated between different users. We want to design a technique that optimally allocates the streams in order to maximize the sum-rate [BH 07]. A 12 B C All Rights Reserved © Alcatel-Lucent 2006 Etc…

Block diagonalization based algorithms § The BD algorithm [SSH 04, VVH 03] is a generalization of the ZF precoder for receivers with multiple antennas. A precoding matrix is used in order to block diagonalize the channel. § Some improvements are proposed in [S 06, W 05, P 04]. § The problem of block diagonalization is that the choice of the active eigenmodes belonging to different users can not be optimized. § The multiuser eigenmode transmission (MET) [BH 07] technique tries to solve this problem. -The following equivalent channel is considered where is a submatrix of whose columns correspond to the selected eigenmodes of user k, according to the SVD - is |Ek| x M, where Ek is the set of selected eigenmodes. -How do we choose the set of users and eigenmodes? 13 All Rights Reserved © Alcatel-Lucent 2006

Choosing users and eigenmodes for MET § For a given transmission interval, we need to determine the set T of users and eigenmodes to allocate so that the weigheted sum rate performance metric R(T) is maximized: Qo. S weights. Power allocation, function precoding matrix and T of MET § Given M transmit antennas and K users, each with N antennas (assume N<M), there are up to KN eigenmodes to choose from, but the base can only provide M. Finding the optimum set requires a brute-force search over all possible allocation of 1, 2, …, M eigenmodes. §The following greedy algorithm is proposed (based on [DS 05]) algorithm works in a greedy manner and chooses up to M modes for transmission. 1. For a given set of eigenmodes, find the eigenmode among the unallocated ones that maximizes the metric. 2. If the metric is higher with the new eigenmode, keep it and goto step 1. Otherwise, exit. 14 All Rights Reserved © Alcatel-Lucent 2006

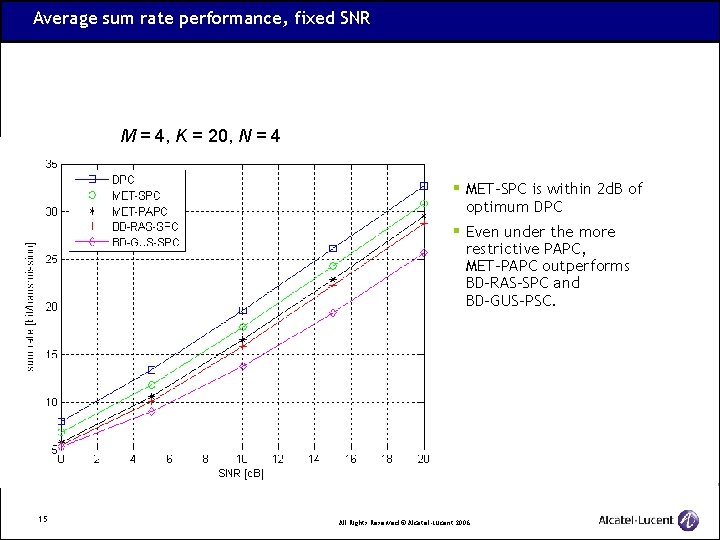
Average sum rate performance, fixed SNR M = 4, K = 20, N = 4 § MET-SPC is within 2 d. B of optimum DPC § Even under the more restrictive PAPC, MET-PAPC outperforms BD-RAS-SPC and BD-GUS-PSC. 15 All Rights Reserved © Alcatel-Lucent 2006

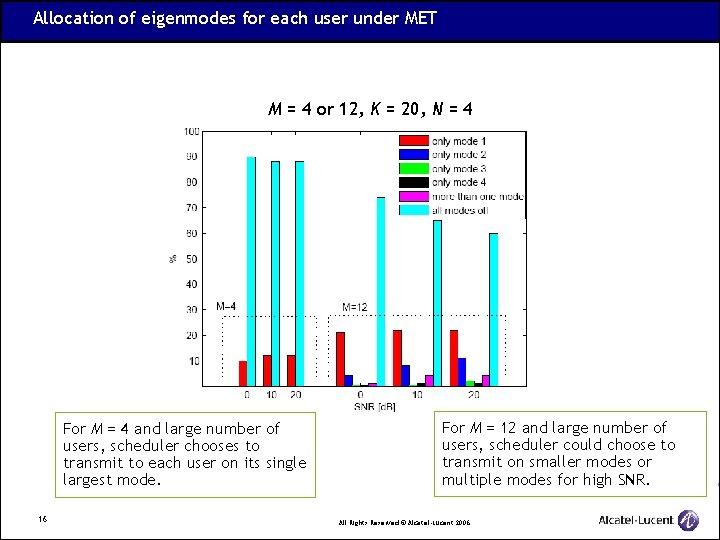
Allocation of eigenmodes for each user under MET M = 4 or 12, K = 20, N = 4 For M = 4 and large number of users, scheduler chooses to transmit to each user on its single largest mode. 16 For M = 12 and large number of users, scheduler could choose to transmit on smaller modes or multiple modes for high SNR. All Rights Reserved © Alcatel-Lucent 2006

SDMA schemes with partial CSI SDMA with estimated or partial CSI: § Jindal, Love, Honig, Heath, Caire, Cioffi, Goldsmith, Huang, Boccardi, Trivellato. Random beamforming techniques: § Sharif, Hassibi, Viswanath, Tse, Laroia Papadias, Avidor. Multiuser multiplexing with interference cancellation at the receiver: § Heath, Andrews, Airy, … Beamforming with fixed codebook: § PU 2 RC: Samsung proposal for UMTS LTE, grid of beams: Alcatel, Ericsson. Sectorization. 17 All Rights Reserved © Alcatel-Lucent 2006

ZF with partial CSI § Each receiver sends to the transmitter a channel direction information (CDI) and a channel quality information (CQI) [J 06]. § Each receiver quantizes the “direction” of its channel vector to a unit norm vector, selected from a quantization codebook formed by 2 B unit norm column vectors § The quantization criterion is minimum chordal distance § Each user feeds back the channel quantization index to the transmitter, which requires B bits. Moreover, each user is assumed to use an independently generated codebook. § We assume a random vector quantization (RVQ) scheme, where the 2 B quantization codewords are independently chosen from an isotropic distribution on the unit sphere. § RVQ gives a lower bound in terms of performance! 18 All Rights Reserved © Alcatel-Lucent 2006

Beamforming design § The beamformer is calculated at the transmitter side by using the CDIs collected from the K users where the channel of the selected users is given by § The power allocated to each user is the same (no waterfilling!) § The SINR at the kth receiver is given by § The SINR cannot be exactly computated neither at the TX side nor at the RX side! § A good estimation of the SINR is very important for the user selection task. 19 All Rights Reserved © Alcatel-Lucent 2006

CQI feedback/SINR estimation A first approach is to consider no quantization error (perfect cancellation of the interference with ZF precoding) and approximate the channel with its projection along the quantized direction A second approach takes into account the quantization error by averaging with respect to the statistic of the quantization codebooks (that affect the interference term) A third approach considers a worse lower bound, but with only one CQI feedback 20 All Rights Reserved © Alcatel-Lucent 2006

ZF with partial CSI – user selection schemes § Original user selection scheme [JGJ 06] ITERATE: 1) Identification of a quasi-orthogonal set of users 2) Selection of best candidate in the quasi-orthogonal set § the following lower bound for the SINR estimation is used § drawback: The parameter is difficult to optimize. If it is chosen too small, chances are that very few users are scheduled for transmission. If it is large, the transmitter may select unwanted users that cause too much interference. 21 All Rights Reserved © Alcatel-Lucent 2006

ZF with partial CSI – user selection schemes § Algorithm 1: It’s a simple extension of the scheme proposed by Dimic and Sidiropoulus for the case of perfect CSI. The users are added successively one at a time, up to a maximum of Ntx if the estimated achievable throughput is increased. Any of previous described CQI feedbackmethods can be used to estimate the users’ SINRs. § Algorithm 2: The drawback of Algorithm 1 is that, under imperfect CSI, it use SINR estimates that are lower bounds of the real SINRs. The consequence of this is that it allocates too a few users. Representing the possible sets of selected users as paths in a tree, a modified scheme just consider more “candidates leaves”. 22 All Rights Reserved © Alcatel-Lucent 2006

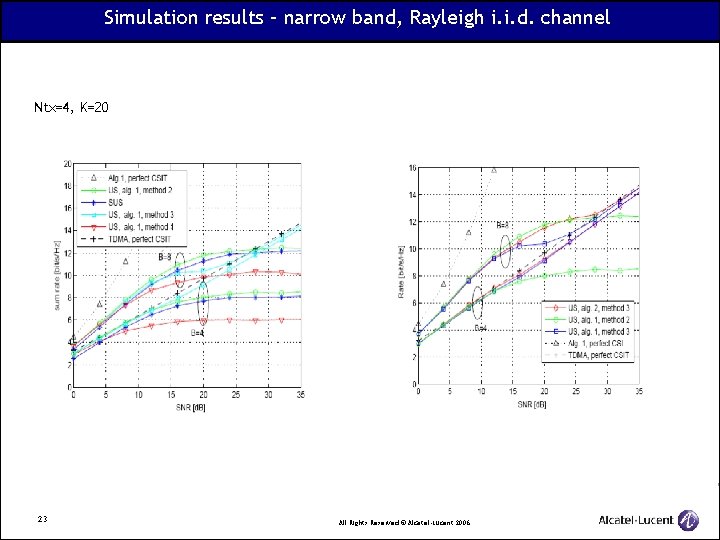
Simulation results – narrow band, Rayleigh i. i. d. channel Ntx=4, K=20 23 All Rights Reserved © Alcatel-Lucent 2006

Extension to multiple receive antennas (MET-MMSE) § An extension of the previous ZF with partial CSI scheme is represented by a modified MET, where a CDI and CQI are fed back for each eigenmode. § For practical systems (ex. : 3 sectors with 4 transmit antennas each and receivers with 2 antennas), even though multiple streams could be sent to a single user (and these streams could be jointly detected), the dominant eigenmode it is almost always the one scheduled for the transmission to a given user. § This effect is even more pronounced in the case of imperfect CSI at the transmitter side, because weaker modes would be the most affected by the effect of the quantization error. § For this reason, for the case of partial CSI at the transmitter side, we only consider the case of dominant eigenmode transmission [BHT 07]. 24 All Rights Reserved © Alcatel-Lucent 2006

MET-MMSE: brief description Phase I Processing at the transmit side -Send common pilots to the K users in the systems Processing at the kth receive side -Calculate the SVD of single user channel matrix and select the Hermitian of the left eigenvector associated to the dominant eigenmode as combining vector. -Calculate and send to the transmitter CDI and the CQI. Phase II Processing at the transmit side -Use CQI and CDI to select a set of active users, and the precoding matrix associated to this set. -Send a dedicated pilot for each selected user, in order to estimate the equivalent channel (channel+precoder). Processing at the kth receive side -MMSE detector. 25 All Rights Reserved © Alcatel-Lucent 2006

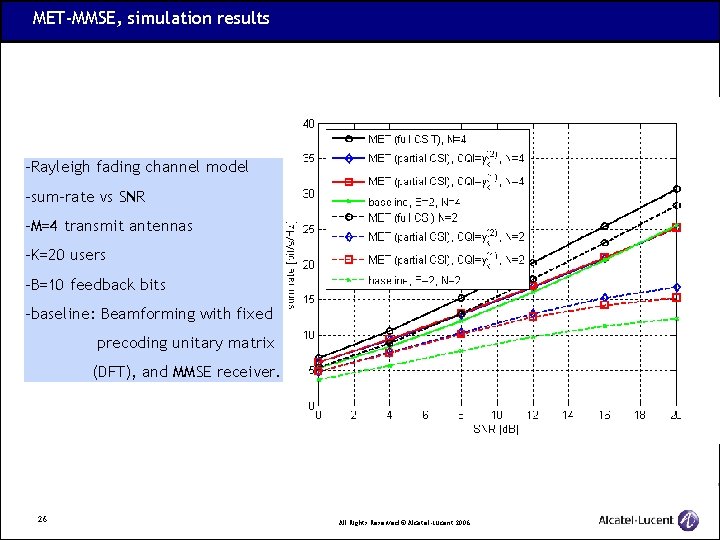
MET-MMSE, simulation results -Rayleigh fading channel model -sum-rate vs SNR -M=4 transmit antennas -K=20 users -B=10 feedback bits -baseline: Beamforming with fixed precoding unitary matrix (DFT), and MMSE receiver. 26 All Rights Reserved © Alcatel-Lucent 2006

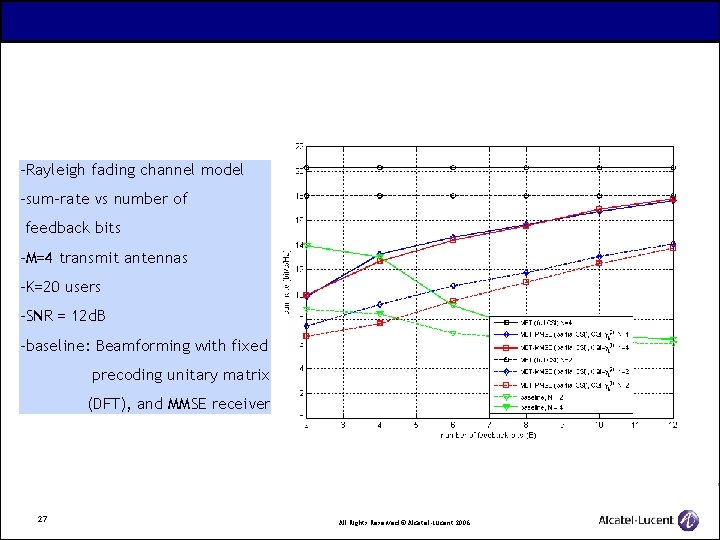
-Rayleigh fading channel model -sum-rate vs number of feedback bits -M=4 transmit antennas -K=20 users -SNR = 12 d. B -baseline: Beamforming with fixed precoding unitary matrix (DFT), and MMSE receiver. 27 All Rights Reserved © Alcatel-Lucent 2006

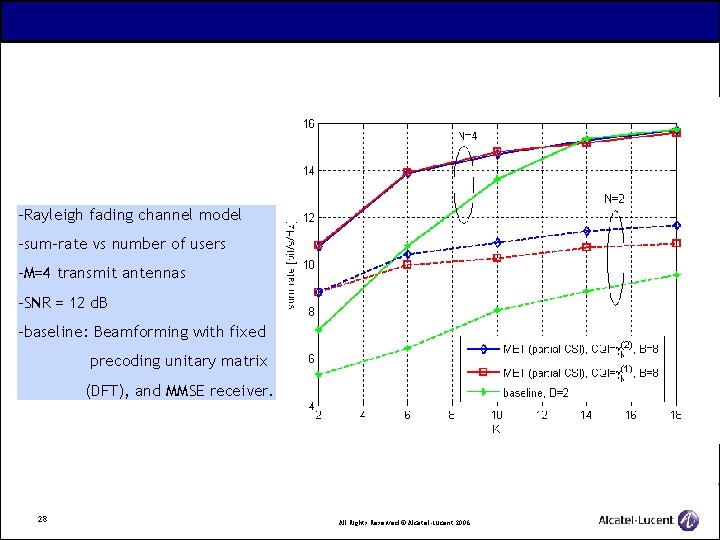
-Rayleigh fading channel model -sum-rate vs number of users -M=4 transmit antennas -SNR = 12 d. B -baseline: Beamforming with fixed precoding unitary matrix (DFT), and MMSE receiver. 28 All Rights Reserved © Alcatel-Lucent 2006

Thanks for your attention! contacts: Federico Boccardi Wireless/Broadband Access Networks Bell Labs Research e-mail: fb@alcatel-lucent. com Tel: +44 -(0)1793 -776670 29 All Rights Reserved © Alcatel-Lucent 2006

References [BGPV 06] H. Boelcskei, D. Gesbert, C. B. Papadias and A. J. van der Veen, editors, Space-Time Wireless Systems: From Array Processing to MIMO Communications. Cambridge University Press, 2006. [BH 06] F. Boccardi, H. Huang, “Zero-forcing precoding for the MIMO-BC under per antenna power constraints, ” IEEE SPAWC, July 2006. [BH 07] F. Boccardi, H. Huang, “A Near-optimum technique using linear precoding for the MIMO broadcast channel, ” IEEE ICASSP 2007, to appear. [BHT 07] F. Boccardi, H. Huang and M. Trivellato “Multiuser eigenmode transmission for MIMO broadcast channels with limited feedback”, submitted to SPAWC 07. [BTC 06] F. Boccardi, F. Tosato and G. Caire, “Precoding schemes for the MIMO-GBC”, International Zurich Seminar on Communication, Zurich, Feb. 2006. [C 83] M. Costa “Writing on Dirty Paper, ” IEEE Trans. Info. Th. , Vol. 29, No. 33, pp. 439 -441, 1983. [CS 03] G. Caire and S. Shamai (Shitz), “On the achievable throughput of a multiantenna Gaussian broadcast channel, ” IEEE Trans. Inform. Theory, vol. 49, pp. 1691– 1706, July 2003. 30 All Rights Reserved © Alcatel-Lucent 2006

[DS 05] G. Dimic and N. D. Sidiropoulos, “On downlink beamforming with greedy user selection: performance analysis and a simple new algorithm, ” IEEE Trans. Commun. , vol. 53, pp. 3857– 3868, Oct. 2005. [J 06] N. Jindal, “MIMO broadcast channels with finite rate feedback, ” IEEE Trans. Inform. Theory, vol. 52, pp. 5045– 5060, Nov. 2006. [PHS 05] C. B. Peel, B. M. Hochwald and A. L. Swindlehurst, “A vector-perturbation technique for near -capacity multi-antenna multi-user communication - part II: perturbation, ” IEEE Trans. Commun. , vol. 53, pp. 537– 544, March 2005. [P 04] Z. Pan, K. -K. Wong and T. -S. Ng, “Generalized multiuser orthogonal spacedivision multiplexing, ” IEEE Trans. Wireless Commun. , vol. 3, pp. 1969– 1973, Nov. 2004. [S 06] Z. Shen, R. Chen, J. G. Andrews, R. W. Heath, Jr. , and B. L. Evans, “Low complexity user selection algorithms for multiuser MIMO systems with block diagonalization, ” IEEE Trans. Signal Process. , vol. 54, pp. 3658– 3663, Sept. 2006. 31 All Rights Reserved © Alcatel-Lucent 2006

[SSH 04] Q. H. Spencer, A. L. Swindlehurst and M. Haardt, “Zero-forcing methods for downlink spatial multiplexing in multiuser MIMO channels”, IEEE Trans. Signal Process. , vol. 52, pp. 461 -471, Feb. 2004 [TBT 07] M. Trivellato, F. Boccardi and F. Tosato, “User Selection Schemes for MIMO Broadcast Channels with Limited Feedback”, IEEE Vehicular Technology Conference, Dublin, Ireland, April 2007. [VJG 03] S. Vishwanath, N. Jindal and A. Goldsmith, "Duality, achievable rates and sum-rate capacity of Gaussian MIMO Broadcast Channels", IEEE Transactions on Information Theory, Vol. 49, No. 10, Oct. 2003, pp. 2658 -2668. [VT 03] P. Viswanath and D. Tse, “Sum capacity of the vector Gaussian channel and uplink-downlink duality, ” IEEE Trans. Inform. Theory, vol. 49, pp. 1912– 1921, Aug. 2003. [VVH 04] H. Viswanathan, S. Venkatesan and H. Huang, “Downlink capacity evaluation of cellular networks with known-interference cancellation, ” IEEE J. Select. Areas Commun. , vol. 21, pp. 802– 811, June 2003. 32 All Rights Reserved © Alcatel-Lucent 2006

[YG 06] T. Yoo, A. Goldsmith, “On the optimality of multiantenna broadcast scheduling using zeroforcing beamforming, ” IEEE J. Sel. Areas Comm, ” Vol. 24, No. 3, pp. 528 -541, Mar. 2006. [YJG 06] T. Yoo, N. Jindal and A. Goldsmith, “Multi-Antenna Broadcast Channels with Limited Feedback and User Selection, ” submitted to IEEE J. Select. Areas Commun. , 2006. [YC 04] W. Yu and J. Cioffi, “Sum capacity of Gaussian vector broadcast channels, ” IEEE Trans. Inform. Theory, vol. 50, pp. 1875– 1892, Sept. 2004. 33 All Rights Reserved © Alcatel-Lucent 2006