MIDSEGMENT THEOREM OBJECTIVE To use properties of midsegments

MIDSEGMENT THEOREM OBJECTIVE: To use properties of midsegments to solve problems BIG IDEA: Coordinate Geometry ESSENTIAL UNDERSTANDINGS: • To draw a midsegment, students must find the midpoint of two sides of a triangle and draw the segment joining the midpoints. • The midsegment of a triangle is related to the third side in two ways. MATHEMATICAL PRACTICE: Make sense of problems and persevere in solving them

TERMS Midsegment of a Triangle: a ________ that connects the __________ of two sides of a triangle Midsegments create a second triangle within the original triangle that is similar to the original triangle. They are parallel to their third sides, therefore the slopes are equal. Midsegment Theorem: the ________ connecting the __________ of two sides of a triangle is __________ to the _______ side and is ________ as long

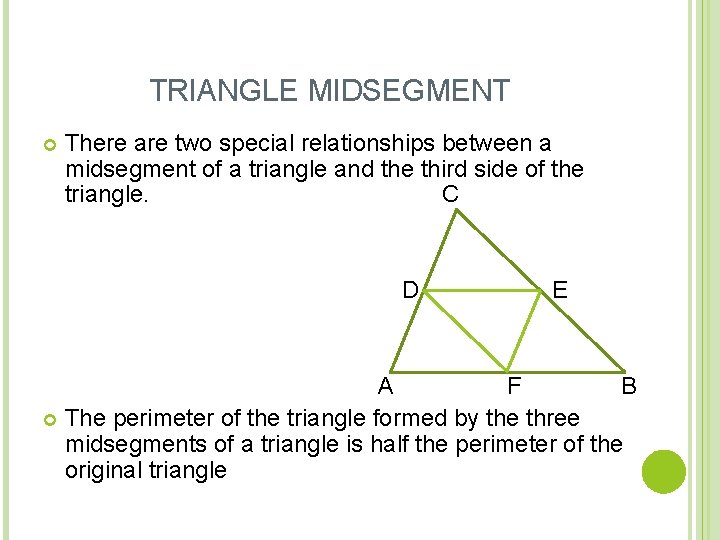
TRIANGLE MIDSEGMENT There are two special relationships between a midsegment of a triangle and the third side of the triangle. C D E A F B The perimeter of the triangle formed by the three midsegments of a triangle is half the perimeter of the original triangle

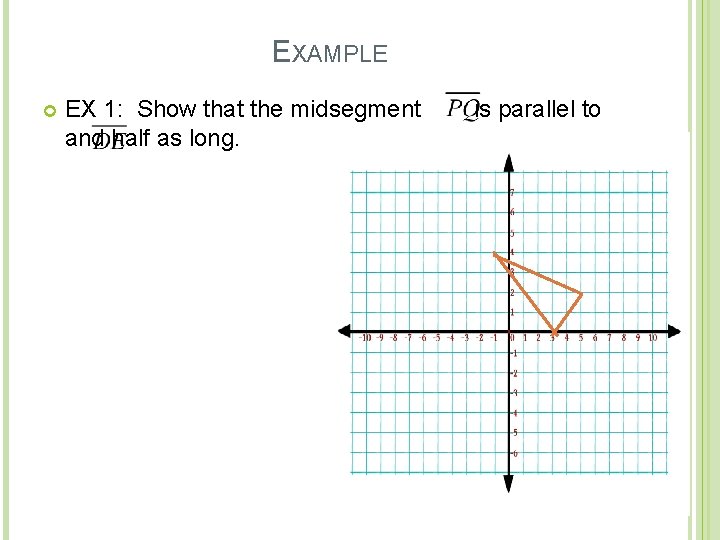
EXAMPLE EX 1: Show that the midsegment and half as long. is parallel to

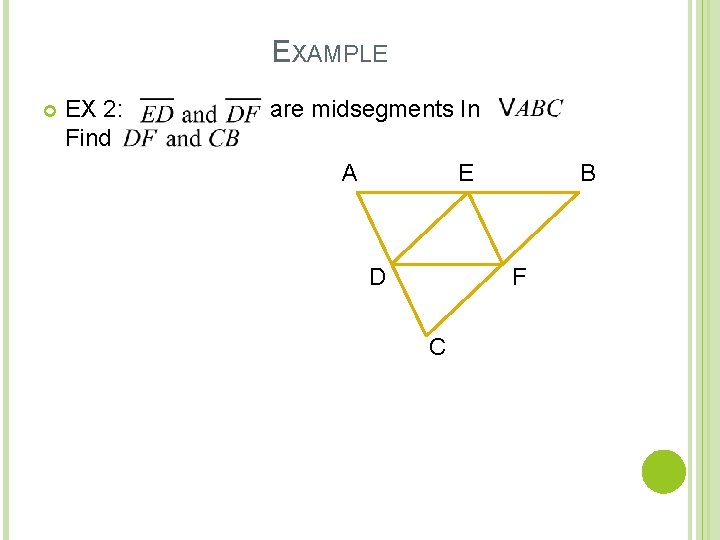
EXAMPLE EX 2: Find are midsegments In A . E D B F C

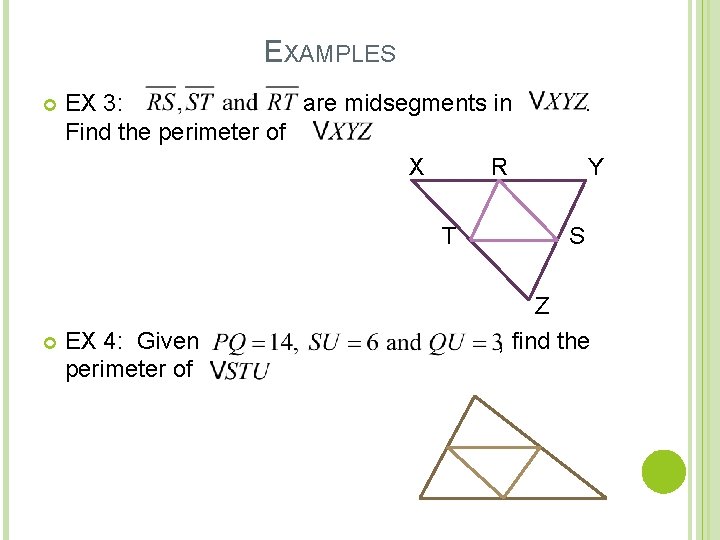
EXAMPLES EX 3: are midsegments in Find the perimeter of X R T EX 4: Given perimeter of . Y S Z , find the

EXAMPLE EX 5: The midpoints of the sides of a triangle are a) What are the coordinates of the vertices of the triangle? b) Find the perimeter of the triangle.

EXAMPLE EX 6: ENVIRONMENTAL SCIENCE A geologist wants to determine the distance, AB, across a sinkhole. Choosing a point E outside the sinkhole, she finds the distances AE and BE. She locates the midpoints C and D of and then measures. What is the distance across the sinkhole?