Midpoint the point that divides the segment into

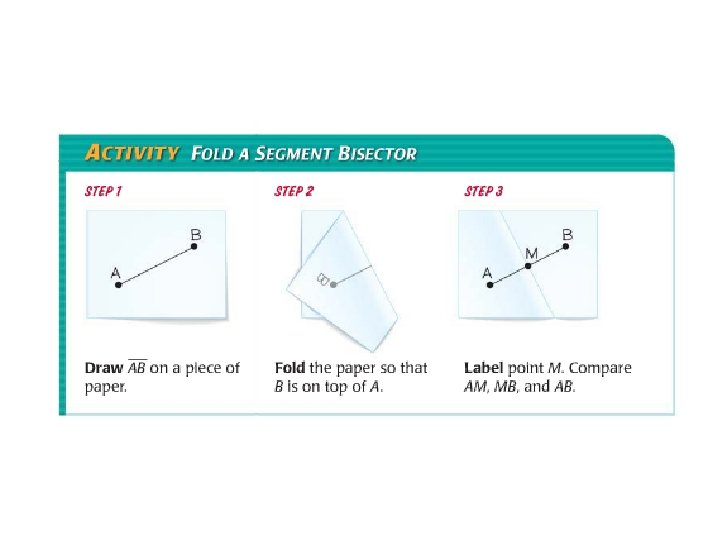
Midpoint: the point that divides the segment into two congruent segments Segment bisector: the point, ray, line segment or plane that intersects the segments at its midpoint.

EXAMPLE 1 Find segment lengths Skateboard In the skateboard design, VW bisects XY at point T, and XT = 39. 9 cm. Find XY. SOLUTION Point T is the midpoint of XY. So, XT = TY = 39. 9 cm. XY = XT + TY Segment Addition Postulate = 39. 9 + 39. 9 Substitute. Add. = 79. 8 cm

EXAMPLE 2 Use algebra with segment lengths ALGEBRA Point M is the midpoint of VW. Find the length of VM. SOLUTION STEP 1 Write and solve an equation. Use the fact that VM = MW 4 x – 1 = 3 x + 3 x– 1=3 x=4 Write equation. Substitute. Subtract 3 x from each side. Add 1 to each side.

EXAMPLE 2 STEP 2 Use algebra with segment lengths Evaluate the expression for VM when x = 4. VM = 4 x – 1 = 4(4) – 1 = 15 So, the length of VM is 15. Check: Because VM = MW, the length of MW should be 15. If you evaluate the expression for MW, you should find that MW = 15. MW = 3 x + 3 = 3(4) +3 = 15

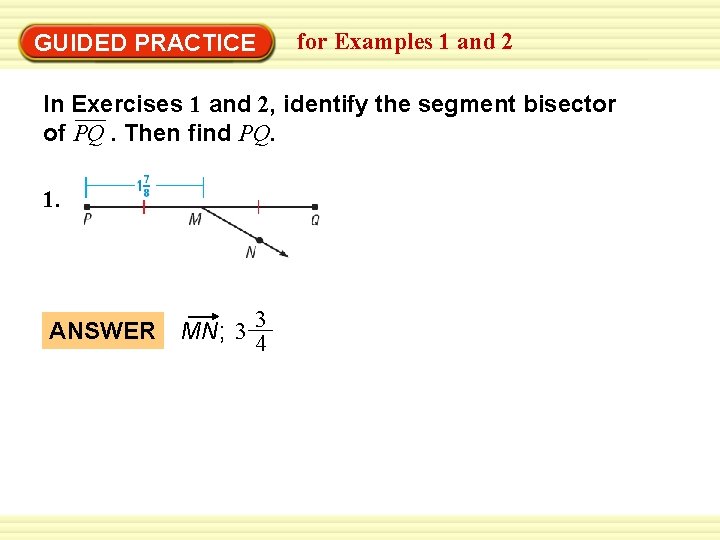
GUIDED PRACTICE for Examples 1 and 2 In Exercises 1 and 2, identify the segment bisector of PQ. Then find PQ. 1. ANSWER 3 MN; 3 4

GUIDED PRACTICE for Examples 1 and 2 In Exercises 1 and 2, identify the segment bisector of PQ. Then find PQ. 2. ANSWER 5 line l ; 11 7

The Midpoint Formula If A(X 1, Y 1) and B(X 2, Y 2) are points in a coordinate plane, then the midpoint M of AB has coordinates X 1 + X 2, Y 1 + Y 2 2 2

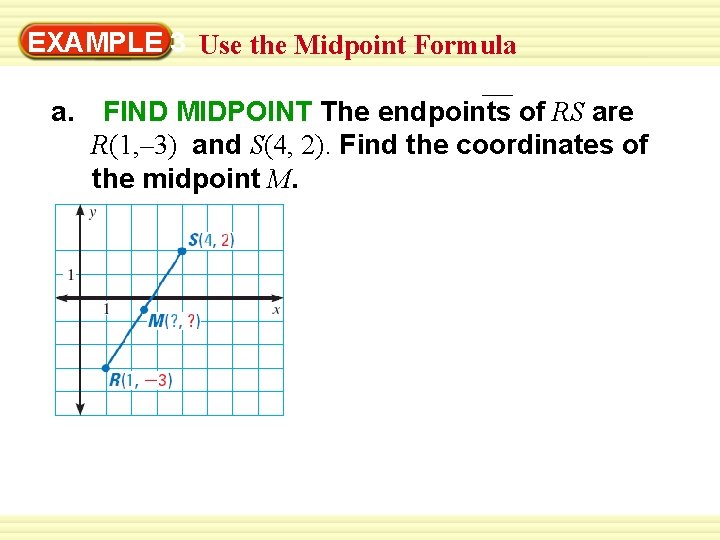
EXAMPLE 3 Use the Midpoint Formula a. FIND MIDPOINT The endpoints of RS are R(1, – 3) and S(4, 2). Find the coordinates of the midpoint M.

EXAMPLE 3 Use the Midpoint Formula SOLUTION a. FIND MIDPOINT Use the Midpoint Formula. , – 3 + 2 = M 5, – 1 M 1+ 2 2 2 42 ANSWE R The coordinates of the midpoint M are 5 , – 1 2 2

EXAMPLE 3 Use the Midpoint Formula b. FIND ENDPOINT The midpoint of JK is M(2, 1). One endpoint is J(1, 4). Find the coordinates of endpoint K.

EXAMPLE 3 Use the Midpoint Formula SOLUTION FIND ENDPOINT Let (x, y) be the coordinates of endpoint K. Use the Midpoint Formula. STEP 1 Find x. 1+ x = 2 2 1+x=4 x=3 STEP 2 Find y. 4+ y 1 2 = 4+y=2 y=– 2 ANSWE The coordinates of endpoint K are (3, – 2 R

GUIDED PRACTICE for Example 3 3. The endpoints of AB are A(1, 2) and B(7, 8). Find the coordinates of the midpoint M. ANSWE (4, 5) R 4. The midpoint of VW is M(– 1, – 2). One endpoint is W(4, 4). Find the coordinates of endpoint V. ANSWE (– 6, – 8) R

Homework: P. 19: 1 -29 odd

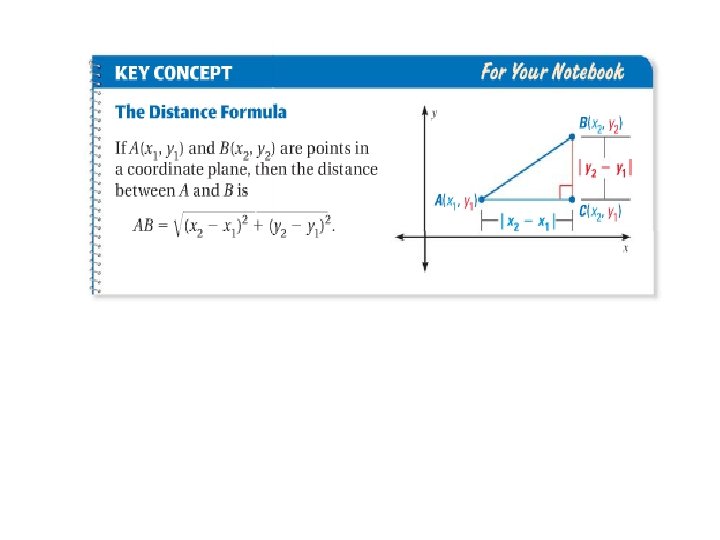
EXAMPLE 4 Standardized Test Practice SOLUTION Use the Distance Formula. You may find it helpful to draw a diagram.

EXAMPLE 4 Standardized Test Practice 2 2 RS = (x 2 – x 1 ) + (y 2 – 1 y ) = = ~ = 2 Distance Formula 2 [(4 – 2)] + [(– 1) – 3] Substitute. 2 2 (2) + (– 4 ) 4+1 6 20 4. 47 Subtract. Evaluate powers. Add. Use a calculator to approximate the square root. ANSWE The correct answer is C. R

GUIDED PRACTICE for Example 4 5. In Example 4, does it matter which ordered 1 (x , y ) and pair you choose to substitute 1 for 2 2 which ordered pair you choose to substitute for (x , y )? Explain. SAMPLE ANSWER No, when squaring the differences in the coordinates, you get the same answer as long as you choose the x and y values from the same point.

GUIDED PRACTICE for Example 4 6. What is the approximate length of AB , with endpoints A(– 3, 2) and B(1, – 4)? 6. 1 units 7. 2 units 8. 5 units 10. 0 units ANSWE R B

Homework: p. 20: 31 -49 odd, plus 48