Microwave Spectrum of Hydrogen Bonded Hexafluoroisopropanol water Complex

Microwave Spectrum of Hydrogen Bonded Hexafluoroisopropanol water Complex Abhishek Shahi Prof. E. Arunan Group Department of Inorganic and Physical Chemistry Indian Institute of Science Bangalore-12, India.

Outline �Introduction to the monomers and the complex �Guess geometry and structure optimization �Spectrum of complex and its isotopologues �Assignment and Discussion �Nature of interaction �Conclusion

Complex under Study HFIP • • • Water HFIP : Hexa. Fluoro. Iso. Propanol Water : H 2 O

Introduction: HFIP-monomer � Two conformers at room temperature (IR studies). � Anti-periplanar (AP) is more stable than Synclinical (SC) in gas phase. Suhm M. Journal of Physical Chemistry A, 2000, 104(2), 265– 274 � Rotational Spectroscopy of monomer �Complete structural determination of monomer. �Microwave spectrum of 6 isotopologues (parent, two deuterated, three C-13) �Only AP conformer could be seen in supersonic expansion. SC AP ek Shahi and E. Arunan, Colloquium. and OSU-2013, http: //hdl. handle. net/1811/55298

Introduction: Water �Monomer �One of the most important molecules for life. �A good H-bond acceptor as well as donor. �Point Group: C 2 v. �Two non-equivalent lone pairs. �Clusters �Experimentally observed up to decamer. �Titled complex always competed with water dimer.

Introduction to the HFIP H 2 O complex: Properties , usefulness and past studies � Binary aqueous solution of HFIP (fluoroalcohol) stabilizes α-helical structure of protein. N. Hirota-Nakaoka and Y. Goto, Bioorg. Med. Chem. 1999, 7, 67. R. Rajan and P. Balaram, Int. J. Pept. Protein Res. 1996, 48, � HFIP is a commonly used solvent for dissolving polymer such 328. as polyethylene terephthalate (PET), a normally difficult-to-dissolve polymer. � HFIP can act as both H-bond donor as well as acceptor. � IR, Raman, X-ray, NMR, MD simulation Studies are known for the HFIP • • • water complexes in liquid and gas phase. Czarnik-Matusewicz, B. ; Pilorz, S. ; Zhang, L. -P. ; Wu, Y. J. Mol. Struct. 2008, 883 -884, 195. Yoshida, K. ; Yamaguchi, T. Chem. Phys. 2003, 119, 6132– 6142. � These studies suggest a very strong bond between HFIP and water.

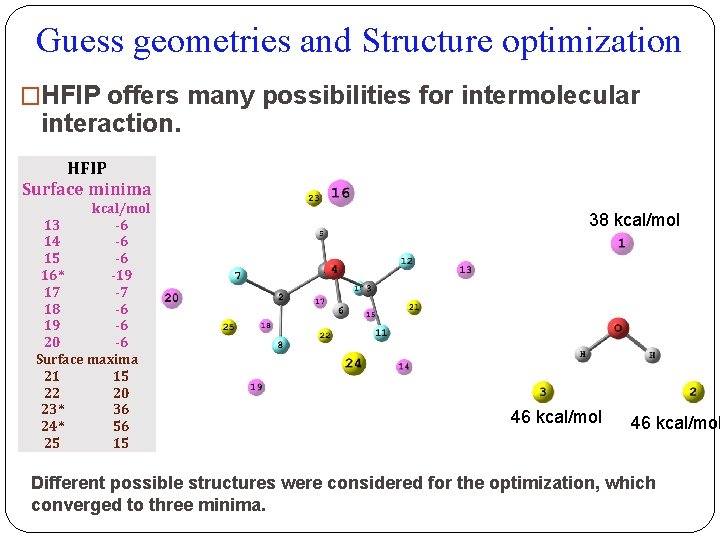
Guess geometries and Structure optimization �HFIP offers many possibilities for intermolecular interaction. HFIP Surface minima kcal/mol 13 -6 14 -6 15 -6 16* -19 17 -7 18 -6 19 -6 20 -6 Surface maxima 21 15 22 20 23* 36 24* 56 25 15 38 kcal/mol 46 kcal/mol Different possible structures were considered for the optimization, which converged to three minima.

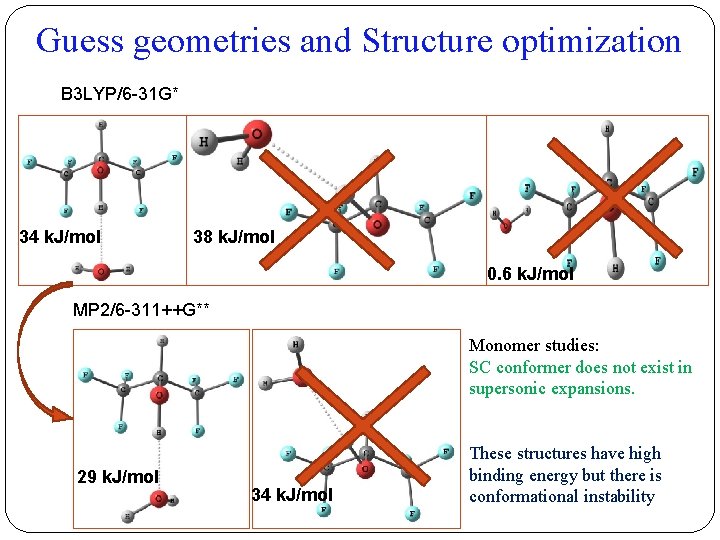
Guess geometries and Structure optimization B 3 LYP/6 -31 G* 34 k. J/mol 38 k. J/mol 0. 6 k. J/mol MP 2/6 -311++G** Monomer studies: SC conformer does not exist in supersonic expansions. 29 k. J/mol 34 k. J/mol These structures have high binding energy but there is conformational instability

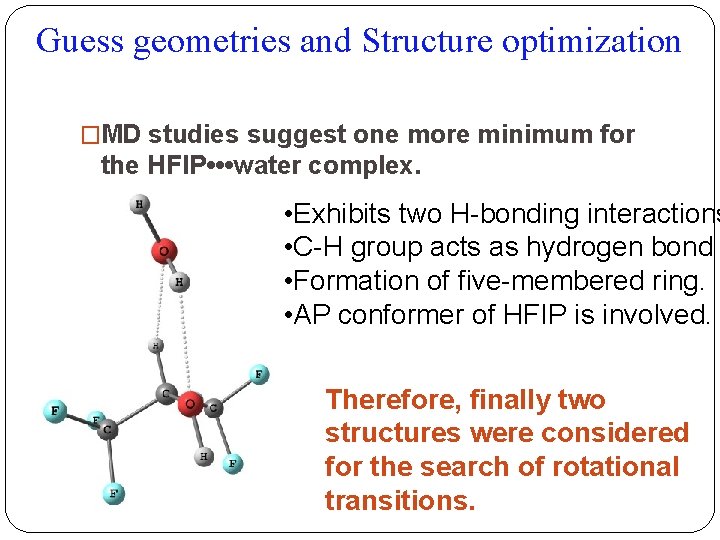
Guess geometries and Structure optimization �MD studies suggest one more minimum for the HFIP • • • water complex. • Exhibits two H-bonding interactions • C-H group acts as hydrogen bond • Formation of five-membered ring. • AP conformer of HFIP is involved. Therefore, finally two structures were considered for the search of rotational transitions.

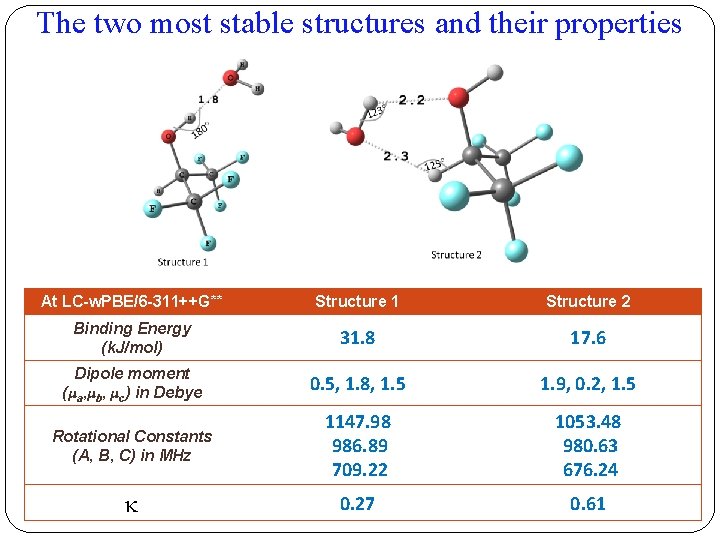
The two most stable structures and their properties At LC-w. PBE/6 -311++G** Structure 1 Structure 2 Binding Energy (k. J/mol) 31. 8 17. 6 Dipole moment (μa, μb, μc) in Debye 0. 5, 1. 8, 1. 5 1. 9, 0. 2, 1. 5 Rotational Constants (A, B, C) in MHz 1147. 98 986. 89 709. 22 1053. 48 980. 63 676. 24 0. 27 0. 61

Search for rotational transitions �On the basis of calculated rotational constants, search was started for following sets of lines. Transitions 5, 0, 5 <-- 4, 1, 4 5, 1, 5 <-- 4, 0, 4 Calculated (MHz) 7427. 03 7429. 15 Observed (MHz) 7401. 5900 7403. 1100 6, 0, 6 <-- 5, 1, 5 6, 1, 6 <-- 5, 0, 5 8843. 63 8843. 95 8812. 6180 8812. 8320 7, 0, 7 <-- 6, 1, 6 7, 1, 7 <-- 6, 0, 6 10259. 55 10259. 60 10223. 1295 10223. 1685 8, 0, 8 <-- 7, 1, 7 8, 1, 8 <-- 7, 0, 7 11675. 38 11675. 39 11633. 5880 �At the end, 46 transitions were observed and could be fitted within experimental uncertainty using a semi -rigid rotor Hamiltonian.

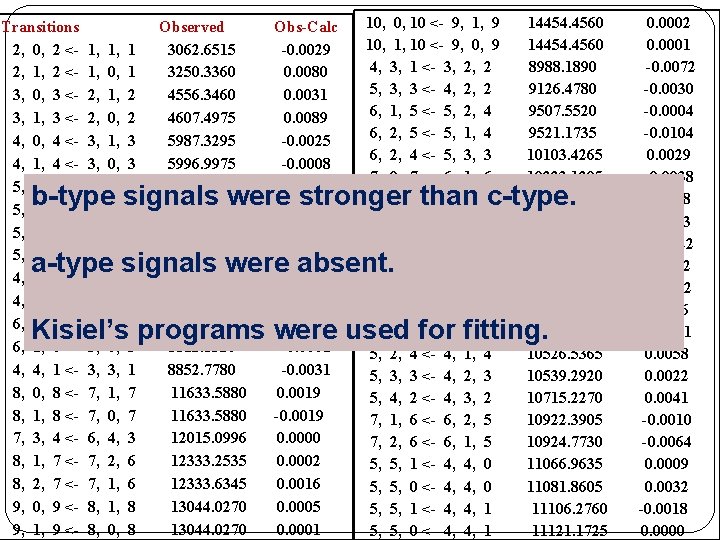
Transitions 2, 0, 2 <2, 1, 2 <3, 0, 3 <3, 1, 3 <4, 0, 4 <4, 1, 4 <5, 0, 5 <5, 1, 5 <5, 2, 4 <5, 2, 3 <4, 4, 1 <4, 4, 0 <6, 0, 6 <6, 1, 6 <4, 4, 1 <8, 0, 8 <8, 1, 8 <7, 3, 4 <8, 1, 7 <8, 2, 7 <9, 0, 9 <9, 1, 9 <- 1, 1, 2, 2, 3, 3, 4, 4, 3, 3, 5, 5, 3, 7, 7, 6, 7, 7, 8, 8, 1, 0, 1, 3, 3, 3, 1, 0, 4, 2, 1, 1, 0, 1 1 2 2 3 3 4 4 3 2 0 0 5 5 1 7 7 3 6 6 8 8 Observed 3062. 6515 3250. 3360 4556. 3460 4607. 4975 5987. 3295 5996. 9975 7401. 5900 7403. 1100 8139. 8660 8434. 5610 8760. 1525 8799. 4635 8812. 6180 8812. 8320 8852. 7780 11633. 5880 12015. 0996 12333. 2535 12333. 6345 13044. 0270 Obs-Calc -0. 0029 0. 0080 0. 0031 0. 0089 -0. 0025 -0. 0008 -0. 0005 -0. 0069 0. 0052 0. 0015 -0. 0008 -0. 0050 0. 0044 -0. 0001 -0. 0031 0. 0019 -0. 0019 0. 0000 0. 0002 0. 0016 0. 0005 0. 0001 10, 0, 10 <- 9, 1, 9 10, 1, 10 <- 9, 0, 9 4, 3, 1 <- 3, 2, 2 5, 3, 3 <- 4, 2, 2 6, 1, 5 <- 5, 2, 4 6, 2, 5 <- 5, 1, 4 6, 2, 4 <- 5, 3, 3 7, 0, 7 <- 6, 1, 6 7, 1, 7 <- 6, 0, 6 5, 4, 2 <- 4, 3, 1 5, 3, 2 <- 4, 2, 2 6, 3, 4 <- 5, 2, 3 <- 4, 1, 3 5, 1, 4 <- 4, 0, 4 5, 4, 1 <- 4, 3, 1 5, 2, 4 <- 4, 1, 4 5, 3, 3 <- 4, 2, 3 5, 4, 2 <- 4, 3, 2 7, 1, 6 <- 6, 2, 5 7, 2, 6 <- 6, 1, 5 5, 5, 1 <- 4, 4, 0 5, 5, 0 <- 4, 4, 0 5, 5, 1 <- 4, 4, 1 5, 5, 0 <- 4, 4, 1 14454. 4560 8988. 1890 9126. 4780 9507. 5520 9521. 1735 10103. 4265 10223. 1295 10223. 1685 10257. 7875 10264. 5755 10354. 0435 10397. 9045 10516. 2925 10523. 6245 10526. 5365 10539. 2920 10715. 2270 10922. 3905 10924. 7730 11066. 9635 11081. 8605 11106. 2760 11121. 1725 b-type signals were stronger than c-type. a-type signals were absent. Kisiel’s programs were used for fitting. 0. 0002 0. 0001 -0. 0072 -0. 0030 -0. 0004 -0. 0104 0. 0029 -0. 0038 0. 0058 0. 0013 -0. 0022 -0. 0002 0. 0016 -0. 0001 0. 0058 0. 0022 0. 0041 -0. 0010 -0. 0064 0. 0009 0. 0032 -0. 0018 0. 0000

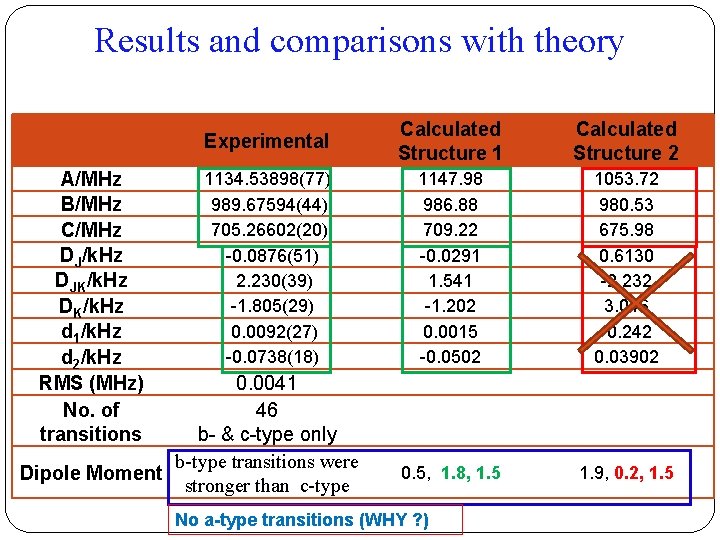
Results and comparisons with theory A/MHz B/MHz C/MHz DJ/k. Hz DJK/k. Hz DK/k. Hz d 1/k. Hz d 2/k. Hz RMS (MHz) No. of transitions Experimental Calculated Structure 1 Calculated Structure 2 1134. 53898(77) 989. 67594(44) 705. 26602(20) -0. 0876(51) 2. 230(39) -1. 805(29) 0. 0092(27) -0. 0738(18) 1147. 98 986. 88 709. 22 -0. 0291 1. 541 -1. 202 0. 0015 -0. 0502 1053. 72 980. 53 675. 98 0. 6130 -2. 232 3. 046 -0. 242 0. 03902 0. 5, 1. 8, 1. 5 1. 9, 0. 2, 1. 5 0. 0041 46 b- & c-type only b-type transitions were Dipole Moment stronger than c-type No a-type transitions (WHY ? )

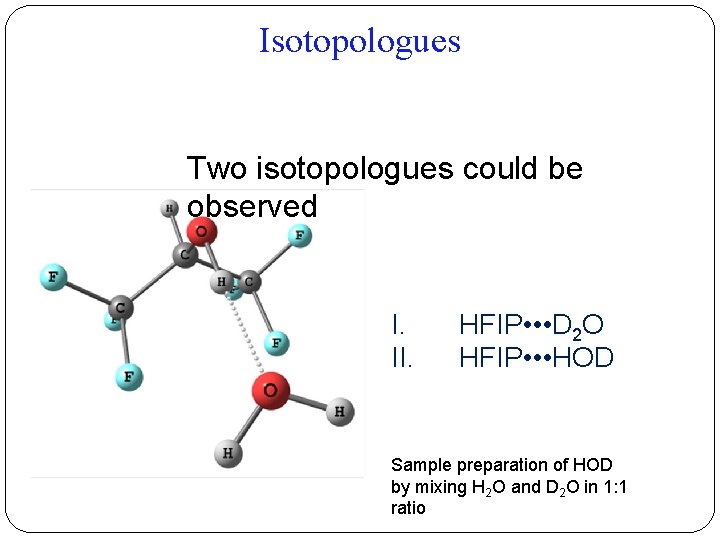
Isotopologues Two isotopologues could be observed I. II. HFIP • • • D 2 O HFIP • • • HOD Sample preparation of HOD by mixing H 2 O and D 2 O in 1: 1 ratio

Rotational Constants of the isotopologues HFIP • • • H 2 O Parent HFIP • • • D 2 O (I) HFIP • • • HOD (II) A /MHz 1134. 53898(77) 1075. 1262(10) 1110. 15554(67) B /MHz 989. 67594(44) C /MHz 705. 26602(20) 683. 64615(22) 696. 72950(21) 983. 0710(16) 986. 0420(17) DJ /k. Hz -0. 0876(51) -0. 148(25) -0. 1737(74) DJK /k. Hz 2. 230(39) 2. 43(16) 3. 526(89) DK /k. Hz -1. 805(29) -1. 91(14) -2. 977(86) d 1 /k. Hz 0. 0092(27) 0. 029(11) [0. 0092] d 2 /k. Hz -0. 0738(18) -0. 0861(57) -0. 1214(39) RMS /MHz 0. 0041 0. 0035 0. 0042 Transition 46 30 33 Both the hydrogens of water are identical.

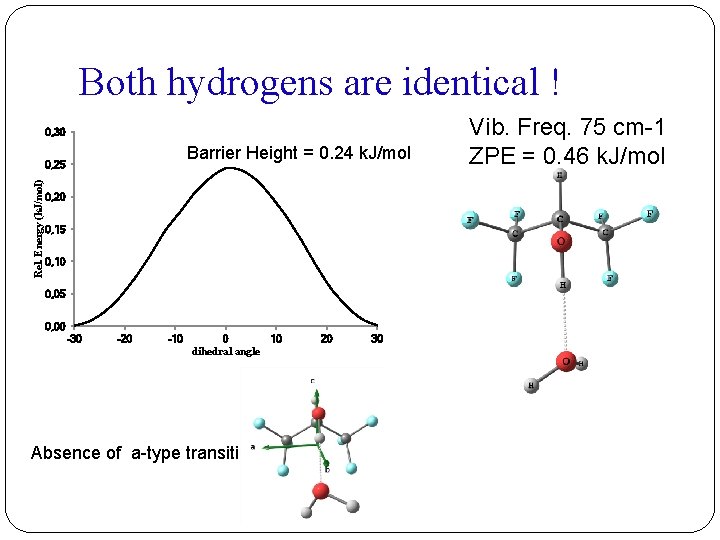
Both hydrogens are identical ! 0, 30 Barrier Height = 0. 24 k. J/mol Rel. Energy (k. J/mol) 0, 25 0, 20 0, 15 0, 10 0, 05 0, 00 -30 -20 -10 0 10 dihedral angle Absence of a-type transition 20 30 Vib. Freq. 75 cm-1 ZPE = 0. 46 k. J/mol

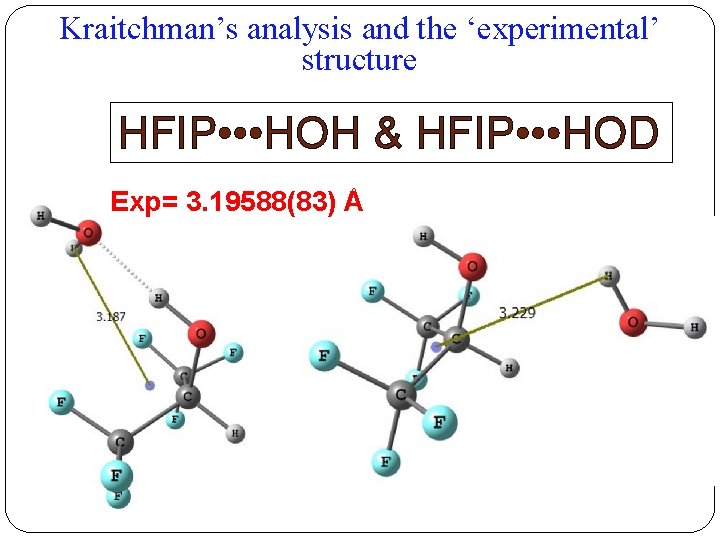
Kraitchman’s analysis and the ‘experimental’ structure HFIP • • • HOH & HFIP • • • HOD Exp= 3. 19588(83) Å

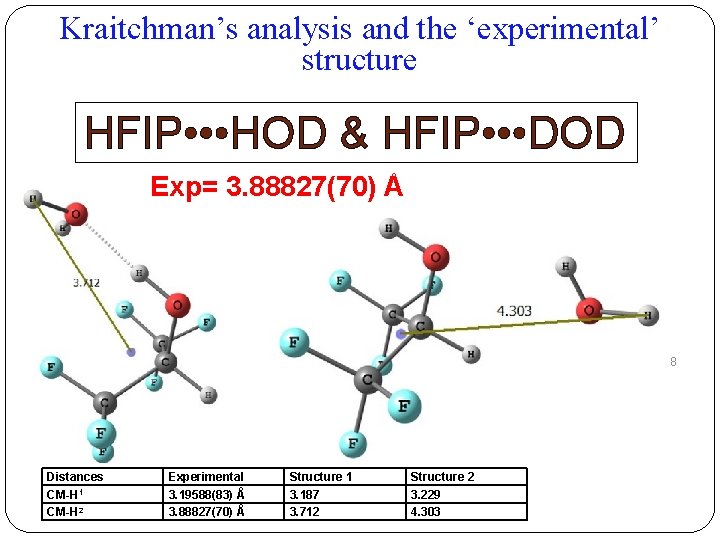
Kraitchman’s analysis and the ‘experimental’ structure HFIP • • • HOD & HFIP • • • DOD Exp= 3. 88827(70) Å 18 Distances CM-H 1 CM-H 2 Experimental 3. 19588(83) Å 3. 88827(70) Å Structure 1 3. 187 3. 712 Structure 2 3. 229 4. 303

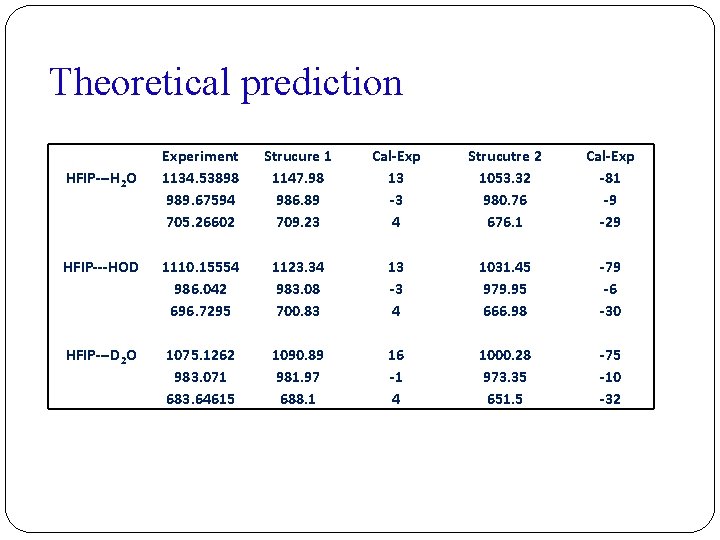
Theoretical prediction Experiment 1134. 53898 989. 67594 705. 26602 Strucure 1 1147. 98 986. 89 709. 23 Cal-Exp 13 -3 4 Strucutre 2 1053. 32 980. 76 676. 1 Cal-Exp -81 -9 -29 HFIP---HOD 1110. 15554 986. 042 696. 7295 1123. 34 983. 08 700. 83 13 -3 4 1031. 45 979. 95 666. 98 -79 -6 -30 HFIP---D 2 O 1075. 1262 983. 071 683. 64615 1090. 89 981. 97 688. 1 16 -1 4 1000. 28 973. 35 651. 5 -75 -10 -32 HFIP---H 2 O

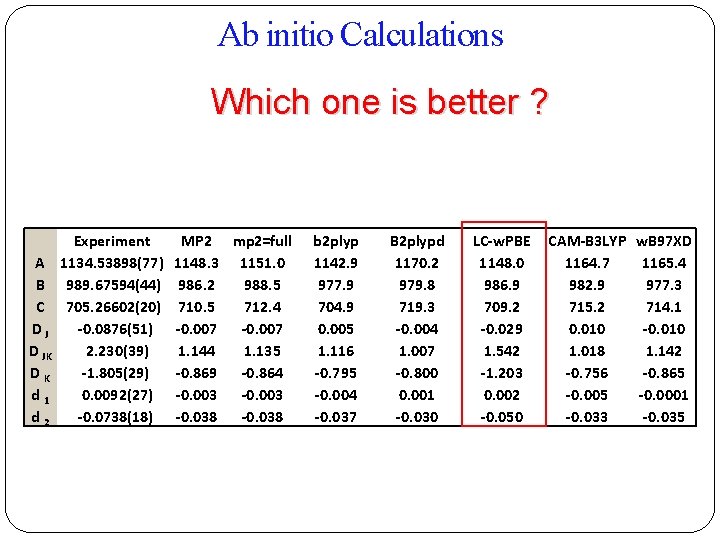
Ab initio Calculations Which one is better ? Experiment A 1134. 53898(77) B 989. 67594(44) C 705. 26602(20) DJ -0. 0876(51) D JK 2. 230(39) DK -1. 805(29) d 1 0. 0092(27) d 2 -0. 0738(18) MP 2 mp 2=full 1148. 3 1151. 0 986. 2 988. 5 710. 5 712. 4 -0. 007 1. 144 1. 135 -0. 869 -0. 864 -0. 003 -0. 038 b 2 plyp 1142. 9 977. 9 704. 9 0. 005 1. 116 -0. 795 -0. 004 -0. 037 B 2 plypd 1170. 2 979. 8 719. 3 -0. 004 1. 007 -0. 800 0. 001 -0. 030 LC-w. PBE 1148. 0 986. 9 709. 2 -0. 029 1. 542 -1. 203 0. 002 -0. 050 CAM-B 3 LYP w. B 97 XD 1164. 7 1165. 4 982. 9 977. 3 715. 2 714. 1 0. 010 -0. 010 1. 018 1. 142 -0. 756 -0. 865 -0. 0001 -0. 033 -0. 035

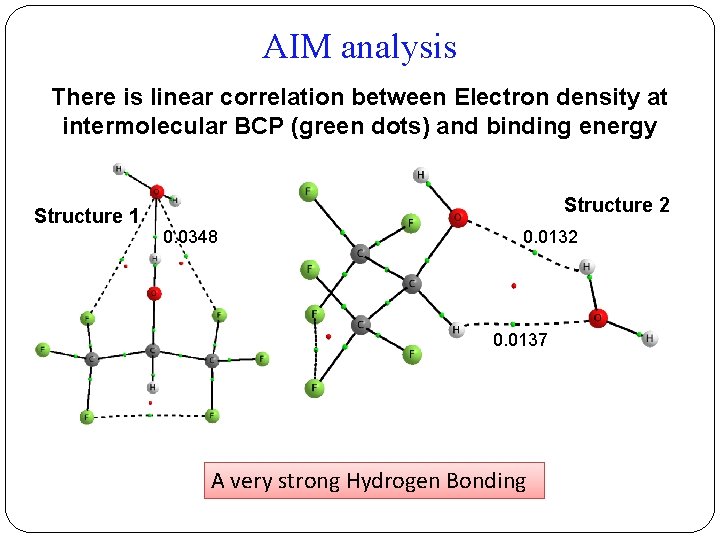
AIM analysis There is linear correlation between Electron density at intermolecular BCP (green dots) and binding energy Structure 1 Structure 2 0. 0348 0. 0132 0. 0137 A very strong Hydrogen Bonding

NBO analysis �One H-bond in Structure 1 �Overlapping of Oxygen’s lone pair of water with O- H( *) of HFIP stabilize the complex by 21. 2 kcal/mol. �Two H-bonds in Structure 2 �Overlapping of Oxygen’s lone pair of water with C- H( *) of HFIP stabilize the complex by 1. 8 kcal/mol. �Overlapping of Oxygen’s lone pair of HFIP with OH( *) of HFIP stabilize the complex by 0. 88 kcal/mol. A very strong Hydrogen Bonding

Summary � Rotational spectra of HFIP---water and its two isotopologues have been observed and fitted within experimental uncertainty. � The fitted rotational constants confirm that the HFIP--water complex exists as structure 1. � A very strong H-bounded complex.

Acknowledgements: All labmates. Funding: