MICROPROCESSOR AND ASSEMBLY LANGUAGE LECTURE1 INTRDUCTION MUHAMMAD HAFEEZ

MICROPROCESSOR AND ASSEMBLY LANGUAGE LECTURE-1 -INTRDUCTION MUHAMMAD HAFEEZ DEPARTMENT OF COMPUTER SCIENCE GC UNIVERSITY LAHORE

TODAY’S AGENDA l Introduction to Course l Background-Prerequisites l l Number System Memory

MY INTRODUCTION Office: Room-103 Course Blog: csience 1234. wordpress. com Email: hafeez 192@gmail. com

COURSE INTRODUCTION l l l Course Title: Microprocessor and Assembly Language Course Code: CS-2207 Recommended Books: l l l 8086 IBM-PC Assembly Language by M. A. Mazidi Intel Microprocessors Architecture, Programming and Interfacing by Bary B. Bray Assembly Language Programming and Organization of the IBM PC By Ytha Y. Yu, Charles Marut

COURSE INTRODUCTION l Reference Material: l l Google It Taste It

COURSE DESCRIPTION l l This is a semester long course introducing fundamentals of a computer organization. Primarily the course focus on Assembly Language for the Intel x 86 series of chips which is the heart of the IBM PC. Assembly Language is a link between microprocessor and High Level Language Write, Understand Debug a Program written in Assembly Language Control I/O Devices

COURSE PREREQUISITES l l Digital Logic Design Minimum familiarity with IBM PC and MSDOS

PROCESSOR UNDERSTANDING l Bottom-Up View l l Logic Gates (Transistors) Flip-Flops, Registers, Multiplexers, Decoders, Adders Memory, Processor, I/O Controllers Build Complete Computer System

PROCESSOR UNDERSTANDING l Top-Down View l A Programmer’s View l l Study tasks that processor executes to execute a HLL program Learn the Set of very basic steps processor performs – Instruction Set l l Can be Learned at Machine Level – difficult to understand Assembly Language Level – Symbolic equivalent to machine level instructions

PROCESSOR UNDERSTANDING l Top-Down View l Example, for the Intel Processor: l l MOV AL, 5 ; Assembly language 101100000101 ; Machine language

MOTIVATION l Link between High Level Language and Assembly l l Assembler is developed for particular processor Reasons to Learns Assembly: l l In-depth understanding of assembly is required to understand device drivers Compiler Development and Code Optimization Helpful in working with Operating System and embedded systems A conceptual bridge between Abstraction of real world in (compiler) and microprocessor

COURSE WORK AND GRADING l l l Quiz-05% Assignment-05% Term Project-10% Mid Term-20% Final Term-60% l This is tentative distribution and liable to change under certain circumstances.

ATTENDANCE &ASSIGNMENT SUBMISSION l l 80% attendance mandatory to qualify for final examination Assignments should be submitted on due date and time, no further extension shall be given. Assignments should be submitted in hard-copy on A 4 paper with proper binding and titled in the format l l Student. First. Name-Roll. No-Course. Code-Section. Assignment. No e. g. kaleem-001 BSCS 14 -CS 2207 -A-01

NUMBER SYSTEM l l l Data Represented in Computer is in the form of digital signals (on-off) Best represented by Binary Number System (1 -0) One binary digit is not enough to represent real world information Need at least 08 bits called a ‘Byte’; that is smallest addressable unit in modern computers For x 86 following units are used l l l 01 Byte = 08 Bits 01 Word = 02 Bytes 01 Double Word = 02 Words

NUMBER SYSTEM l l l The contents of 1 bytes stored in computer memory needs ‘Interpretation’ For Example, the memory content 0100 0001, can be represented as Number 65 or Letter ‘A’ It is upto the programmer to provide interpretation

NUMBER SYSTEM l A written number is only meaningful when we define its Base l l Hexadecimal 25 is written as 25 h Binary 1010 is written as 1010 b Decimal 1010 is written as 1010 or 1010 d Significance of Bases to demonstrate quantity l Larger base represent large quantities in fewer digits

BINARY NUMBER SYSTEM l Digits are 1 and 0 l l 1 = true 0 = false l MSB – Most Significant Bit LSB – Least Significant Bit l Bit Numbering: l

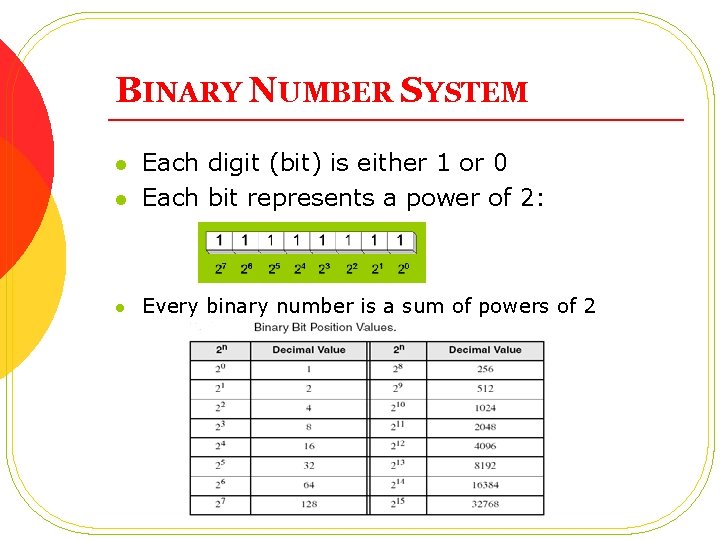
BINARY NUMBER SYSTEM l Each digit (bit) is either 1 or 0 Each bit represents a power of 2: l Every binary number is a sum of powers of 2 l

CONVERTING BINARY TO DECIMAL l Weighted positional notation shows how to calculate the decimal value of each binary bit: l l l Decimal Number = (Dn-1 2 n-1) + (Dn-2 2 n-2) +. . . + (D 1 21) + (D 0 20) D = Binary Digit (1010)2 =1 x 23+0 x 22+1 x 21+0 x 20 =8+0+2+0= (10)10

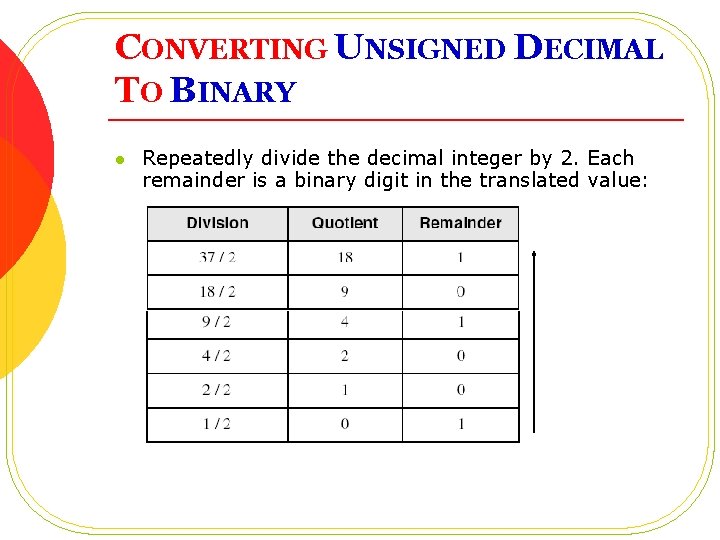
CONVERTING UNSIGNED DECIMAL TO BINARY l Repeatedly divide the decimal integer by 2. Each remainder is a binary digit in the translated value:

BINARY ARITHMETIC l l Binary Addition Binary Subtraction Binary Multiplication Binary Division

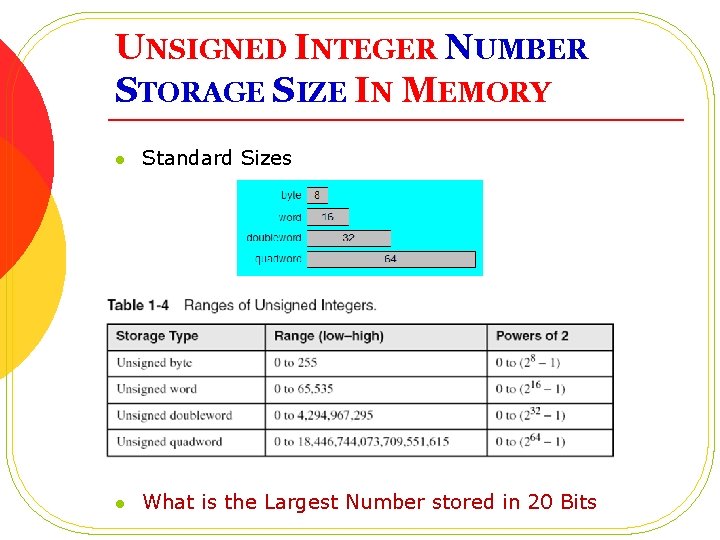
UNSIGNED INTEGER NUMBER STORAGE SIZE IN MEMORY l Standard Sizes l What is the Largest Number stored in 20 Bits

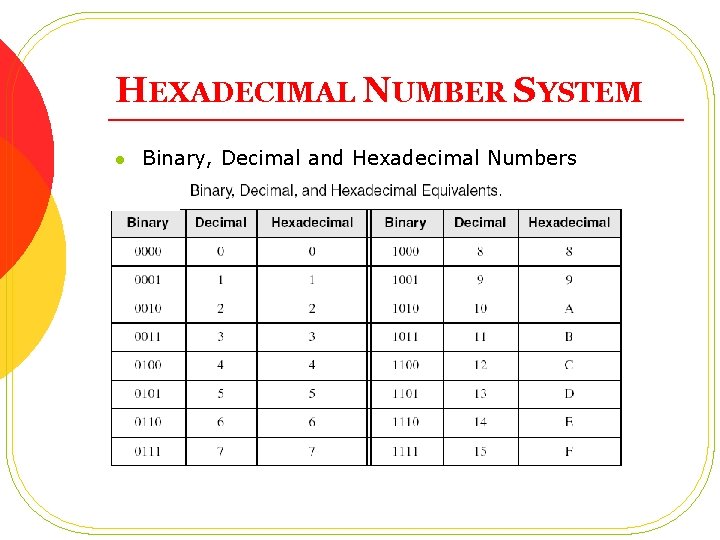
HEXADECIMAL NUMBER SYSTEM l Binary, Decimal and Hexadecimal Numbers

CONVERTING HEXADECIMAL TO BINARY l Each Hexadecimal digit is equivalent to 4 Binary Digits l Prove the same with repeated division method by 2

CONVERTING HEXADECIMAL TO DECIMAL l Multiply each digit by its corresponding power of 16: Decimal = (Dn-1 16 n-1)+…+(D 3 163) + (D 2 162) + (D 1 161) + (D 0 160) l Hex 1234 equals (1 163) + (2 162) + (3 161) + (4 160)= decimal 4, 660. l Hex 3 BA 4 equals (3 163) + (11 * 162) + (10 161) + (4 160)= decimal 15, 268. l Another way

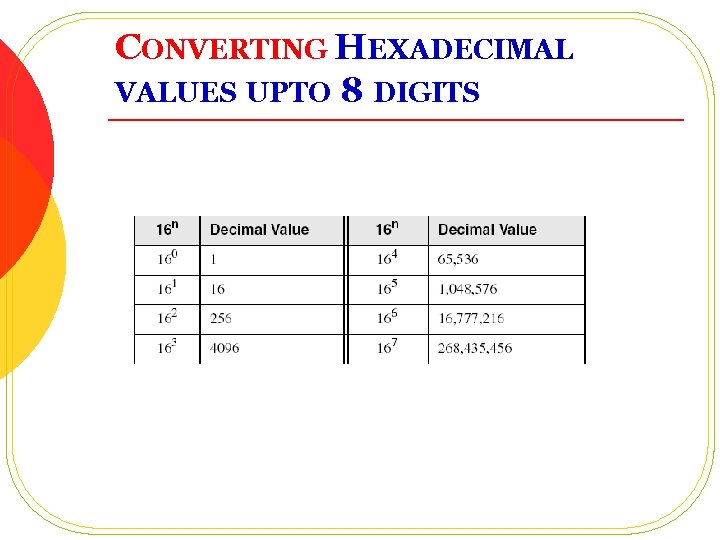
CONVERTING HEXADECIMAL VALUES UPTO 8 DIGITS

CONVERTING DECIMAL TO HEXADECIMAL l decimal 422 = 1 A 6 hexadecimal

HEXADECIMAL ADDITION l l Starting from LSB if sum of each two digits is greater than or equal to 16, divide it with 16, the quotient become carry digit and remainder become sum digit Carry will be 1 36 42 78 28 45 6 D 28 58 80 6 A 4 B B 5 21 / 16 = 1, rem 5 l Important skill to do arithmetic in Hexadecimal for Assembly Language

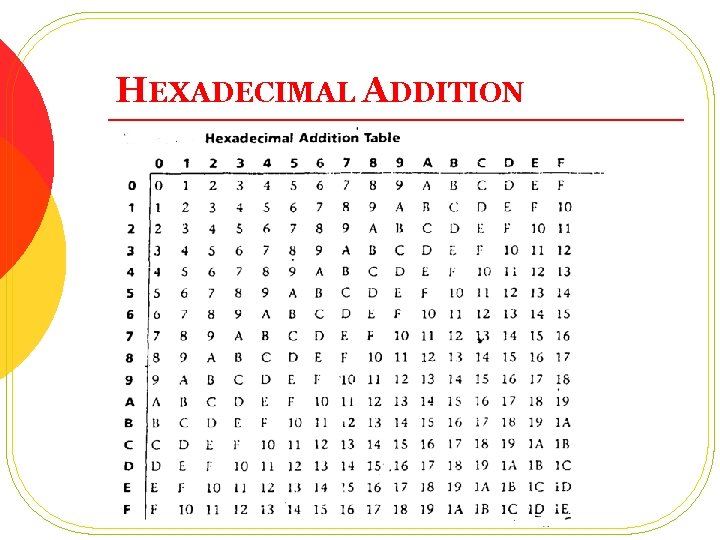
HEXADECIMAL ADDITION

HEXADECIMAL SUBTRACTION l l When a Borrow is required from the digit on left hand side, add sixteen (16) to the digit on right hand side Borrow will be 16 16 + 5 = 21 -1 C 6 A 2 24 l 75 47 2 E The address of var 1 is 00400020. The address of the next variable after var 1 is 0040006 A. How many bytes are used by var 1?

TWO REPRESENTATIONS FOR INTEGERS l The unsigned representation: in that case all the bits are used to represent a magnitude l Can be positive number or Zero l Signed Representation l For What purpose signed number could be used? l Can you recognize a number for even or odd by looking at bit pattern?

SIGNED REPRESENTATIONS FOR INTEGERS l l l l The Singed Representation forms: Sign Magnitude Form Uses most significant bit of the word to represent the sign. l 0 - Positive l 1 - Negative. Rest of the number is encoded in magnitude part 37 = 0000 00100101 -37 = 10000000 00100101 6712 = 00011010 00111000 -6712 = 10011010 00111000 Can represent numbers from -32, 767 to 32, 767. l -215+1. . 215 -1 But, two representations for zero: 0 = 00000000 -0 = 10000000 Arithmetic can be cumbersome.

SIGNED REPRESENTATIONS FOR INTEGERS l l l Sign Magnitude Form Uses most significant bit of the word to represent the sign. l 0 - Positive l 1 - Negative. Rest of the number is encoded in magnitude part 37 = 0000 00100101 -37 = 10000000 00100101 6712 = 00011010 00111000 -6712 = 10011010 00111000 Can represent numbers from -32, 767 to 32, 767. l -215+1. . 215 -1 But, two representations for zero: 0 = 00000000 -0 = 10000000 Arithmetic can be cumbersome.

SIGNED REPRESENTATIONS FOR INTEGERS l l l l l 1’s Compliment Form Negative number is stored as bit-wise complement of corresponding positive number. Leftmost bit of positive number is 0. That of negative number is 1. 196 = 0000 11000100 -196 = 1111 00111011 Can represent numbers from -32, 767 to 32, 767. l -215+1. . 215 -1 Arithmetic is easier than sign-magnitude. But, still have two representations for zero: 0 = 00000000 -0 = 11111111 l Add 5 and -5 using 1’s Complement and see the result?

SIGNED REPRESENTATIONS FOR INTEGERS l l l 2’s Compliment Form Modern Method Positive number represented in same way as other two methods Negative number obtained by taking 1's Complement of positive number and adding 1. 6713 = 00011000 00011101 1's Comp = 11100111 11100010 2's Comp = 11100111 11100011 Word integer can represent numbers from -32, 768 to 32, 767. l -215. . 215 -1 Byte integer can represent numbers from -128 to 127. l -27. . 27 -1 One version of zero: 00000000 Find 2’s complement of 6

SIGNED REPRESENTATIONS FOR INTEGERS l Represent -97 d in 2’s Complement Form using 8 bits and 16 bits? l Sol: Represent 97 in Hex l l l Convert hex representation into binary Take 2’s complement of binary Convert into Hex … this how it is represented 5 ABAH – 2 A 91 H Use 2’s complement to solve it

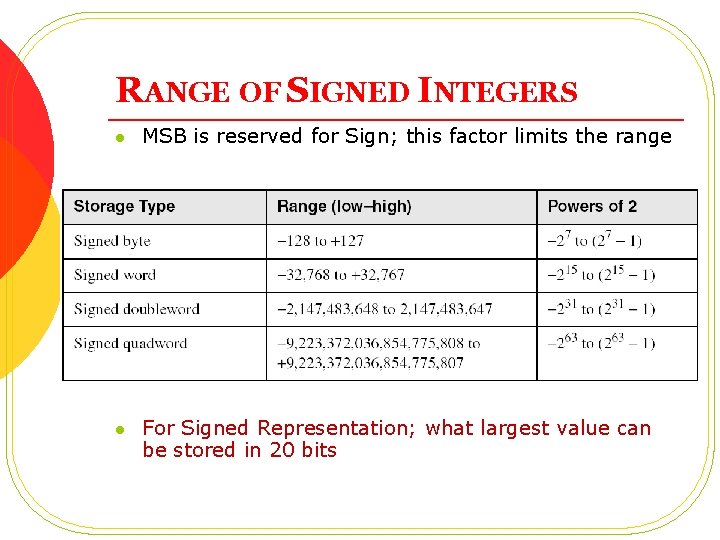
RANGE OF SIGNED INTEGERS l MSB is reserved for Sign; this factor limits the range l For Signed Representation; what largest value can be stored in 20 bits

SIGNED AND UNSIGNED IN COMPUTER MEMORY TO DECIMAL l l l To use a number in computer memory; we need to provide it either signed or unsigned interpretation How can we do that? Unsigned: Just convert binary to decimal, better to convert to hex and then to decimal Signed: If msb=0, convert like unsigned numbers, if msb=1, call the N number as –N, take 2’s complement and then convert to decimal, place – sign in front 1111 can be interpreted as 255 (unsigned) Or -1 (minus one) as signed Its upto the programmer to provide memory contents suitable interpretation for program

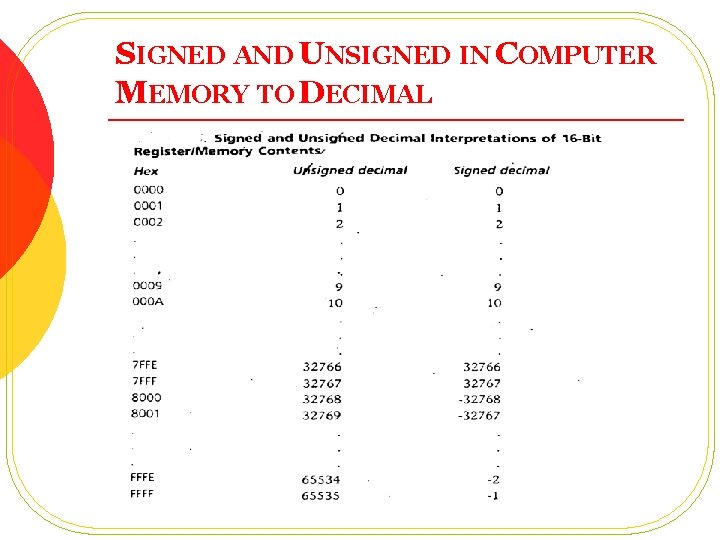
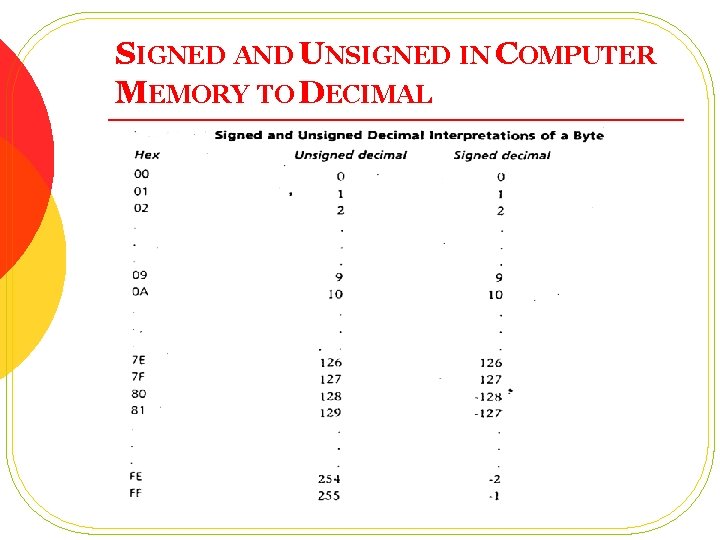
SIGNED AND UNSIGNED IN COMPUTER MEMORY TO DECIMAL

SIGNED AND UNSIGNED IN COMPUTER MEMORY TO DECIMAL l Any Observation in previous two slides? l Computer memory contents are FE 0 CH, give it signed and unsigned representation?

SIGNED AND UNSIGNED IN COMPUTER MEMORY TO DECIMAL l Another Observation: l From 0000 H-7 FFFH Signed Number = Unsigned Numbers From 8000 H-FFFFH Signed Number = Unsigned Number-65536 l Can you Observe the same for Byte? l Give FE 0 CH a singed and unsigned representation through this method? l

MINIMUM AND MAXIMUM VALUES FOR SIGNED NUMBERS l MSB used to represent sign, fever bits left for magnitude representation l For Example, a signed byte have l l l Smallest Positive 0000 (0 in decimal) Largest Positive 0111 1111 (127 in decimal) Smallest Negative 1000 0000 (-128) Largest Negative 1111 (-1) First low byte is stored memory then high byte [Little Endian]

CHARACTER REPRESENTATION THROUGH MEMORY CONTENTS l l Each Character is represented with 7 bit Code called ASCII Character ASCII Code from 00 H to 07 FH l l Codes from 20 H to 7 EH are printable, rest of them are control code An extended character set is obtained by setting the most significant bit (MSB) to 1 (codes 80 h to FFh) so that each character is stored in 1 byte

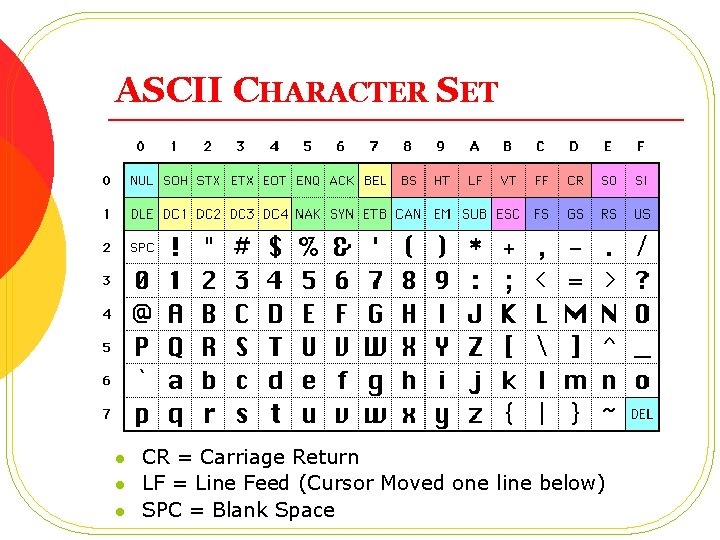
ASCII CHARACTER SET l l l CR = Carriage Return LF = Line Feed (Cursor Moved one line below) SPC = Blank Space

TEXT FILES USING ASCII CHARACTER SET l l Text Files contain printable and non-printable ASCII Characters Different OS represent non-printable characters (control characters) i. e. moving to cursor to start of line through different ways, l l Windows: <CR>+<LF> UNIX: <LF> MAC: <CR> Origin of problem when we move text files from one OS to other

CHARACTER STORAGE l l l ASCII (0 -127) Extended ASCII (0 -255) Uni-Code (0 -65, 535)

QUESTIONS ? ? ? ? ? ?