Microbiology Lab BIO 3126 1 General Information 2

Microbiology Lab BIO 3126 1

General Information • • • 2 Instructor: John Basso Email: jbasso@uottawa. ca Tel. 613 -562 -5800 Poste 6358 Office: BSC 102 My web page: http: //mysite. science. uottawa. ca/jbasso/home. htm • Page web du cours: http: //mysite. science. uottawa. ca/jbasso/microlab/home. htm

My Web Page 3

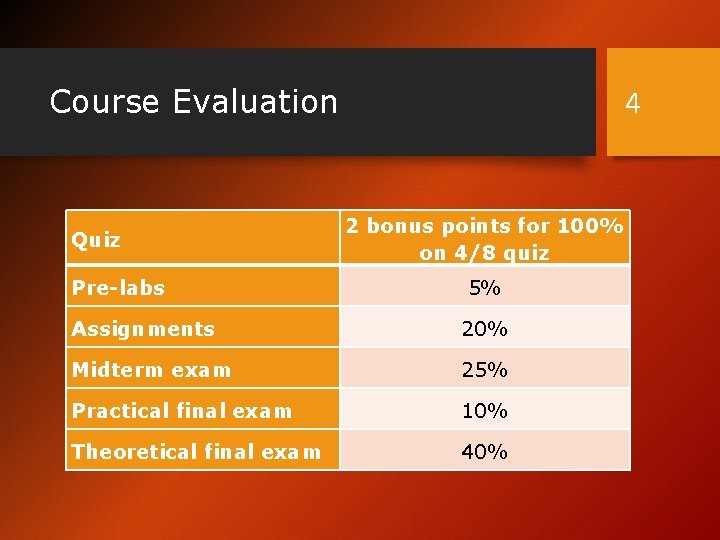
Course Evaluation Quiz Pre-labs 4 2 bonus points for 100% on 4/8 quiz 5% Assignments 20% Midterm exam 25% Practical final exam 10% Theoretical final exam 40%

Solutions 5

Definitions 6 • Solution • Mixture of 2 or more ingredients in a single phase • Solutions are composed of two constituents • Solute (ingredient) • A solid that is being dissolved • Or a stock solution that is being diluted • Solvent (OR Diluent) • Part of solution in which solute is dissolved or stock solution is being diluted

Preparing Solutions • 2 ways to create a solution • By dissolving a solid • By diluting a more concentrated solution • Do your calculations • Final volume required • Mass of solid (solutes) • Volume of stock solutions • Volume of solvent • Add solvent first (usually water) • Add other ingredients to solvent 7

Preparing Solutions • Working with concentrations • Dilutions • Amounts 8

Concentrations • Concentration = Quantity of solute Quantity of solution • Ways to express concentrations: • • Molar concentration (Molarity) Percentages Mass per volume Ratios 9

Molarity 10 • No of Moles of solute/Liter of solution Moles of solute = Mass of solute MM of solute Moles of solute Molarity = Volume in L of solution • Mass of solute : given in grams (g) • Molecular mass (MM) : given as grams per mole (g/mole)

Percentages • Percentage concentrations can be expressed as either: • V/V – volume of solute/100 m. L of solution • M/M – Mass of solute/100 g of solution • M/V – Mass of solute/100 m. L of solution • All represented as fractions of 100 11

Percentages (Cont’d) 12 • %V/V • Ex. 4. 1 L solute/55 L solution =7. 5% • Must have same units top and bottom! • %M/V • Ex. 16 g solute/50 m. L solution =32% • Must have units of same order of magnitude top and bottom! • % M/M • Ex. 1. 7 g solute/35 g solution =4. 9% • Must have same units top and bottom!

Mass per Volume 13 • A mass (amount) per a volume • Ex. 1 kg/L • Know the difference between an amount and a concentration! • In the above example 1 litre contains 1 kg (an amount) • What amount would be contained in 100 ml? • What is the percentage of this solution?

Ratios 14 • A way to express the relationship between different constituents • Expressed according to the number of parts of each component • Ex. 24 ml of chloroform + 25 ml of phenol + 1 ml isoamyl alcohol • Therefore 24 parts + 25 parts + 1 part • Ratio: 24: 25: 1 • How many parts are there in this solution?

Dilutions Reducing a concentration A fraction 15

Dilutions 16 • Dilution = making weaker solutions from stronger ones • Example: Making orange juice from frozen concentrate. You mix one can of frozen orange juice with three (3) cans of water.

Dilutions (Cont’d) 17 • Dilutions are expressed as the volume of the solution being diluted per the total final volume of the dilution • In the orange juice example, the dilution would be expressed as 1/4, for one can of O. J. to a TOTAL of four cans of diluted O. J. When saying the dilution, you would say, in the O. J. example: “one in four”.

Dilutions (Cont’d) 18 • Another example: • If you dilute 1 ml of serum with 9 ml of saline, the dilution would be written 1/10 or said “one in ten”, because you express the volume of the solution being diluted (1 ml of serum) per the TOTAL final volume of the dilution (10 ml total).

Dilutions (Cont’d) 19 • Another example: • One (1) part of concentrated acid is diluted with 100 parts of water. The total solution volume is 101 parts (1 part acid + 100 parts water). The dilution is written as 1/101 or said “one in one hundred and one”.

Dilutions (Cont’d) 20 • Dilutions do NOT have units (cans, ml, or parts) but are expressed as the number parts to the total number of parts • Dilutions are always expressed as a fraction of one • 1 part / total number of parts • Example: 1/10 or “one in ten” • OR: 1/(1+9) • OR 1 part solute/1 part solute + 9 parts solvent

Dilutions (Cont’d) 21 • Dilutions are always expressed with the original substance being diluted as one (1). If more than one part of original substance is initially used, it is necessary to convert the original substance part to one (1) when the dilution is expressed.

Dilutions (Cont’d) 22 • Example: • Two (2) parts of dye are diluted with eight (8) parts of solvent. Total volume of solution = 2 parts dye + 8 parts diluent = 10 parts • The dilution is initially represented as 2/10 • Convert so that the numerator is one (1) • Therefore 1/5

The Dilution Factor 23 • Represents the inverse of the dilution • Expresed as the denominator followed by “X” • EX. A 1/10 dilution represents a dilution factor of 10 X • The dilution factor allows one to determine the original concentration • Final conc. X Dilution factor = Original conc.

Problem • Two parts of blood are diluted with five parts of saline • What is the dilution? 2/(2+5) = 2/7 =1/3. 5 • 10 ml of saline are added to 0. 05 L of water • What is the dilution? 10/(10+50) = 10/60=1/6 24

Working with Parts 25 • Preparation of 110 m. L solution representing a 1/10 dilution • 1/10 th of final volume must be stock solution 1/10 th of 110 m. L = 11 m. L = 1 parts • 9/10 th of final volume must be solvent 9/10 th of 110 m. L = 99 m. L = 9 parts

Working with Parts 26 • A solution is prepared by adding 15 m. L of a stock solution to 75 m. L of solvent. What is the dilution and the volume of 1 part? • Fraction: 15 m. L stock/(15 m. L stock + 75 m. L solvent) • = 15/90 = dilution of 1/6 • Volume of one part • Total volume X the dilution = 90 m. L X 1/6 = 15 m. L

Problem : More than one ingredient • Want to prepare 15 m. L of a solution containing two ingredients (solutes) • Need the following dilutions • Solute “a”: 1/10 • Solute “b”: 1/3 27

Problem : More than one ingredient 28 • Express each dilution over a common denominator • Solute « a » : 1/10 = 3/30 • Solute « b » : 1/3 = 10/30 • Therefore need 3 parts of « a » + 10 parts of « b » + 17 parts of solvent • Total of 13 parts of solute/30 parts of solution • Volume of one part • 30 parts of solution = 25 m. L, therefore 1 part = 0. 83 m. L

Problem : More than one ingredient 29 • 3 parts of solute “a”: 3 X 0. 83 m. L = 2. 49 m. L • 10 parts of solute “b”: 10 X 0. 83 m. L = 8. 3 m. L • 17 parts of solvent: 17 X 0. 83 m. L = 14. 11 m. L

Determining the Required Fraction: (The dilution) Determine the reduction factor (Dilution factor) = 30 What I have What I want Ex. You have a solution at 25 mg/ml and you want to obtain a solution at 5 mg/ml Reduction factor is: 25 mg/ml = 5 (Dilution factor) The fraction is equal to 1/dilution factor = 1/5 (the dilution)

Determining the Required Volumes 31 • Ex. You want 55 m. L of a solution which represents a 1/5 dilution • Use a ratio equation: • 1/5 = x/55 = 11/55 • Therefore 11 m. L of stock/ (55 m. L – 11 m. L) of solvent • = 11 ml of stock/ 44 ml of solvent

Problem 1 32 • Prepare 25 m. L of a 2 m. M solution from a stock of 0. 1 M • What is the dilution required? 2 m. M/100 m. M =1/50 • What volumes of solvent and stock solution are required? Solute: 1/50 X 25 m. L = 0. 5 m. L = 1 part Solvent: 49 parts X 0. 5 m. L OR 25 -0. 5 m. L = 24. 5 m. L

Problem 2 • What volume of a 0. 1 M stock solution should be added to 25 m. L of water to obtain a 2 m. M final concentration ? • What is the dilution required? 2 m. M/100 m. M = 1/50 • Volumes of solute required? 1/50 dilution = 1 part stock/50 parts solution = 1 part stock/1 part stock + 49 parts solvent Volume of solvent = 25 m. L = 49 parts Therefore volume of one part = 25 m. L/49 = 0. 51 m. L 0. 51/(25 +0. 51) = 0. 51/25. 51 = 1/50 33

Serial Dilutions 34 • Dilutions made from dilutions • The dilutions are multiplied • Ex. • A 1: 1/10 • A 2: 1/4 • A 3: 0. 5/1. 5 = 1/3 • Final dilution of the series = (A 1 X A 2 X A 3) = 1/120

Tonicity & Osmolarity 35

Tonicity & Osmolarity 36 • Terms used to describe the relationship between the relative concentrations of solute particles on both sides of a semipermeable membrane and the movement of water • Tonicity only takes into consideration the concentration of impermeable solutes particles • Osmolarity takes into consideration the total concentration of all solute particles • Permeable and impermeable

Measures of Osmolarity & Tonicity 37 • Same units • Number of osmoles (Osm) of particles of solute per liter of solution (Osm/L) • Ex. • 1 molar (1 M) Na. Cl = 1 mole of Na. Cl per litre • 1 mole of Na+ and 1 mole of Cl • Therefore 2 moles of ions per liter • Equivalent to 2 Osm/litre = 2 Os. M

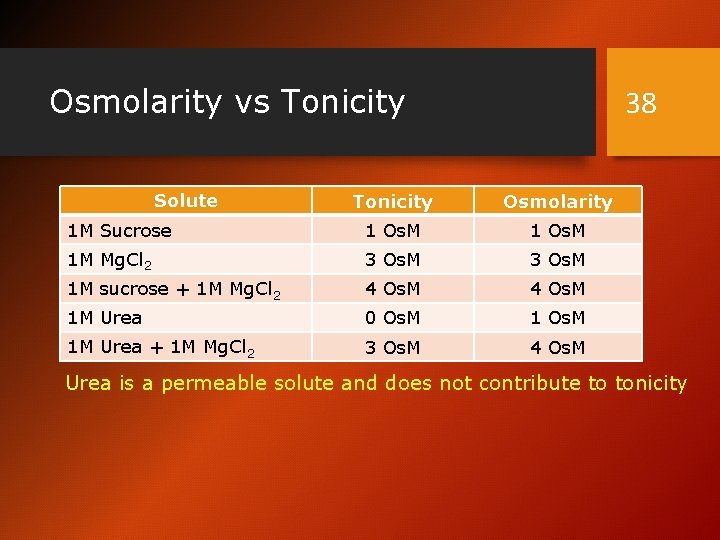
Osmolarity vs Tonicity Solute 38 Tonicity Osmolarity 1 M Sucrose 1 Os. M 1 M Mg. Cl 2 3 Os. M 1 M sucrose + 1 M Mg. Cl 2 4 Os. M 1 M Urea 0 Os. M 1 M Urea + 1 M Mg. Cl 2 3 Os. M 4 Os. M Urea is a permeable solute and does not contribute to tonicity

Osmotic Relationship Inside 1 M Sucrose 1 Os. M 39 Outside 0. 5 M Urea 0. 5 Os. M Cell is hyperosmotic Water will move in

Osmotic Relationship Inside 0. 1 M Sucrose 0. 1 Os. M 40 Outside 0. 5 M Urea 0. 5 Os. M Cell is hypoosmotic Water will move out

Osmotic Relationship Inside 0. 5 M Sucrose 0. 5 Os. M 41 Outside 0. 5 M Urea 0. 5 Os. M Cell is isoosmotic No water movement

Tonic Relationship Inside 1 M Sucrose 1 Os. M 42 Outside 1 M Urea 0 Os. M Cell is hypertonic Water will move in

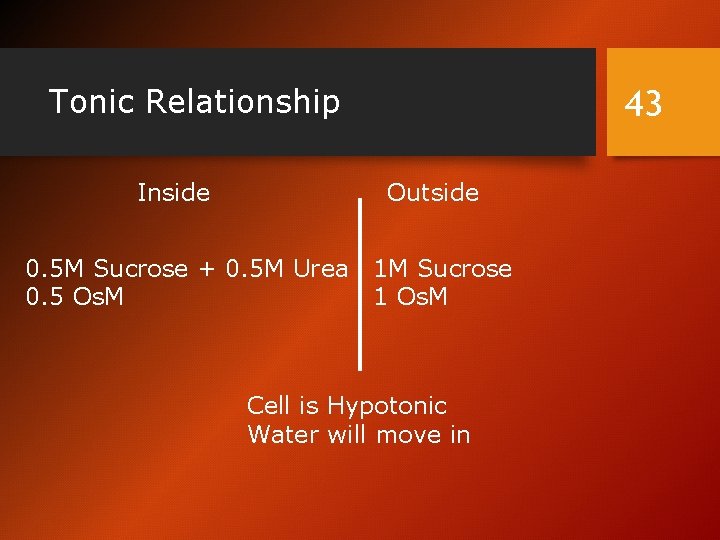
Tonic Relationship Inside 43 Outside 0. 5 M Sucrose + 0. 5 M Urea 1 M Sucrose 0. 5 Os. M 1 Os. M Cell is Hypotonic Water will move in

Tonic Relationship Inside 44 Outside 0. 5 M Sucrose + 0. 5 M Urea 0. 25 M Na. Cl + 0. 5 M Urea 0. 5 Os. M Cell is Isotonic No water movement