Microarray Synthesis through Multiple Use PCR Primer Design

Microarray Synthesis through Multiple -Use PCR Primer Design Research Proficiency Examination Rohan Fernandes 9/26/2020 1

Biology Background: PCR n n PCR animation (From the Dolan DNA Learning Center, CSHL) Applications of PCR include n n n 9/26/2020 Genetic Fingerprinting. Medical Diagnostics. DNA Sequencing. 2

What are Microarrays? 9/26/2020 3

What are Microarrays? n n n A grid with different DNA probes in each location. Allows one to test a given sample for expression of multiple genes. Can compare gene expression by using different colored fluorescent markers in two samples. 9/26/2020 4

Genomic Data n n Sequences are known for more than 800 organisms! 100 free-living species have been sequenced already. But we know very little about most of these organisms’ biology. Exploiting full-genome sequence data, requires investigators to have inexpensive custom microarrays. 9/26/2020 5

Why Microarrays? n n Microarray technology has revolutionized our understanding of gene expression. Applications include n n n 9/26/2020 Cell cycle analysis. Response of cells to environmental stress. Impact of gene knockouts. 6

A Primer Design True Story!! n n Project for Futcher and Leatherwood to design PCR primers for microarray synthesis. Strict criteria for primer length, melting temperature, self-similarity were specified. Designed primers for 5827 and 5012 genes for Cerevisiae and Pombe. PCR done with sample set of primers designed for 96 genes each of S. Pombe and S. Cerevisiae was 100% successful. 9/26/2020 7

The 110, 000 Dollar Problem n n n Good primer design can be crucial in synthesizing microarray DNA. $110, 000 out of a total budget of $220, 000 for microarray synthesis was spent on PCR primers alone. We propose an alternative method of PCR primer design to reduce costs. 9/26/2020 8

Efficiency of PCR n n n Usually, PCR primers are designed to occurs uniquely on the genome. However, efficiency of PCR falls exponentially as length of product increases. PCR becomes ineffective for product sizes beyond 1200 bases. 9/26/2020 9

Exploiting PCR Efficiency Drop-off n n n Amplification is significant only if primers hybridize near each other. We can reuse primers to amplify several genes, provided each primer pair is unique. We can save thousands of primers through reuse! 9/26/2020 10

Who can benefit? n n The total cost of PCR primers may dissuade investigators of less studied organisms from using microarrays. Our technique can reduce costs enough to make microarrays more attractive to less funded researchers. 9/26/2020 11

What is the potential win? n n n Let (n, m) be the (number of genes, minimum number of primers required to amplify them). m primers can result in m(m+1)/2 unique primer pairs. 2 n primers may be sufficient instead of 2 n. Conventional primer design requires 12, 000 primers for 6, 000 genes, but 110 might suffice. In practice this lower bound will be unreachable but there will still be a large win. 9/26/2020 12

Potential Win? (Example) n n n Consider the cost of building a spotted microarray for a 20, 000 gene organism. Conventional techniques will require us to use 40, 000 primers. Cost : $160, 000 at $4 a primer. If 3, 000 primers suffice, cost is only $12, 000. The best case is overoptimistic, but realistic wins are still impressive. 9/26/2020 13

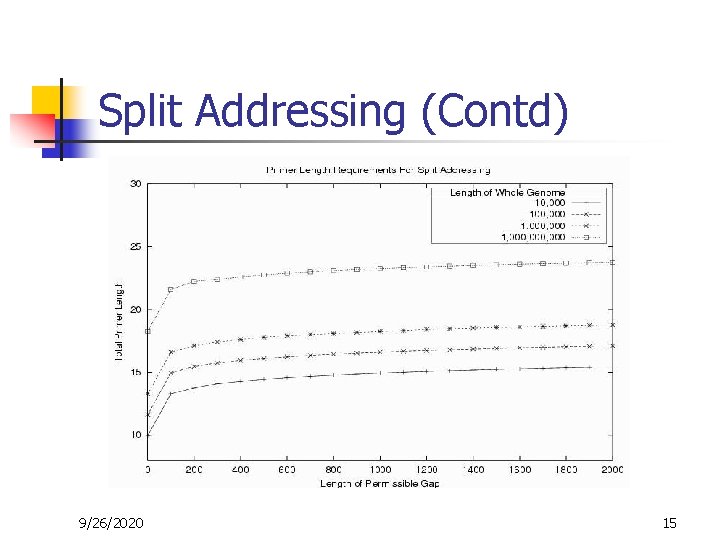
Cost of Split Addressing n What is the probability that two random strings will occur in a long random string in a certain order and with no more than a certain gap? n 9/26/2020 14

Split Addressing (Contd) 9/26/2020 15

Split Addressing – Conclusion n Total length of primers required to ensure uniqueness of hybridization increases only very slowly with the length of the genome. The penalty for genome scale lengths and realistic PCR gap lengths amount to only additional 3 -4 bases of primer over ungapped matching. These results support the potential of multiple -use primers. 9/26/2020 16

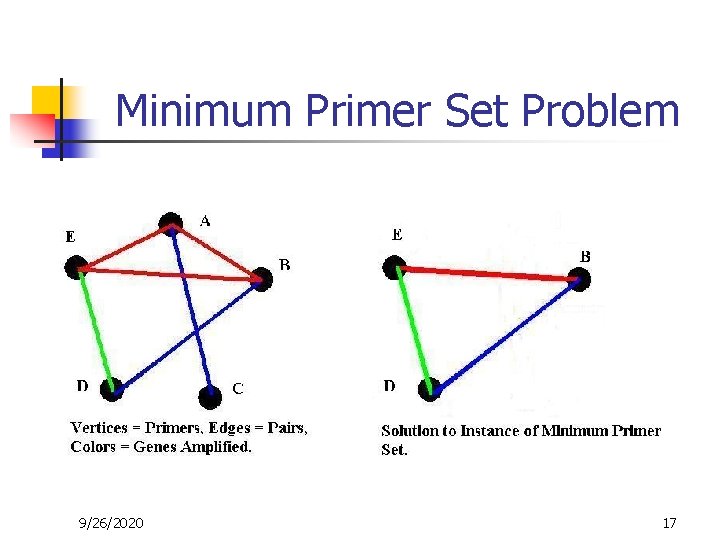
Minimum Primer Set Problem 9/26/2020 17

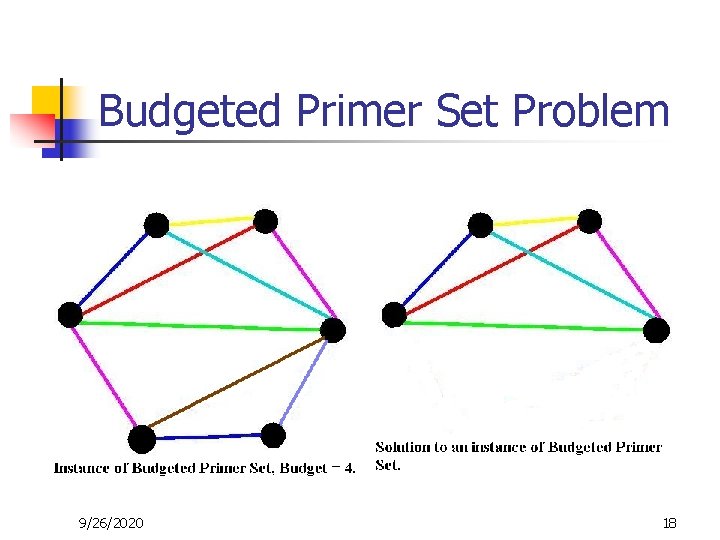
Budgeted Primer Set Problem 9/26/2020 18

Hardness of problems n n n The Minimum Primer Set problem is NPhard and hard to approximate to within a logarithmic factor. The Budgeted Primer Set problem is NPhard and seems to be related to densest k-subgraph problem. Approximation bounds for densest ksubgraph problem are not encouraging. 9/26/2020 19

Reduction Gadget 9/26/2020 20

Reduction from Set Cover to Minimum Primer Set n n (S, X) is a set cover instance. S U, X W. Connect vertex in U to vertex in W iff corresponding set in S contains element from X. Label (color) each edge by the name of the element vertex at its end. MPS solution will include all element vertices and minimum number of set vertices which cover all sets. Q. E. D. 9/26/2020 21

A Heuristic to approximate MPS n n n Based on greedy heuristic to find densest subgraph. Each edge is weighted with the value of (1/number of edges bearing that color). Vertex weight is set to sum of adjoining edge weights. Algorithm proceeds by removal of vertex with minimum weighted vertex without eliminating any color. Algorithm terminates when no more vertices can be eliminated. 9/26/2020 22

Example Run of Algorithm (1) n Initially graph with vertex weights. 9/26/2020 Color Edges Weight Blue 2 Green 1 1/2 1/1 Red 1/3 3 23

Example Run of Algorithm (2) n After removing minimum weighted vertex. 9/26/2020 Color Edges Weight Blue 1 Green 1 1/1 Red 1/3 3 24

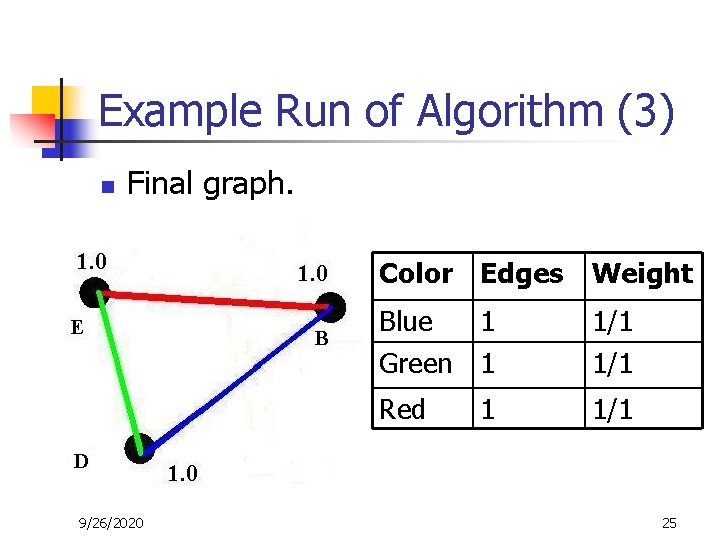
Example Run of Algorithm (3) n Final graph. 9/26/2020 Color Edges Weight Blue 1 Green 1 1/1 Red 1/1 1 25

Performance of Heuristic n n n O(|V|+|E|+|C|)) time and O(|V|+|E|+|C|) space. This heuristic is too slow. It is quadratic in |V| hence very slow on large data sets. For our largest dataset this heuristic produced a solution in two days as opposed to 25 minutes for the next heuristic. 9/26/2020 26

A Linear-time Heuristic n n n We select an edge of each color that has maximum colored adjacency to form our seed graph. We switch an edge for a color if that saves us any vertices in the seed graph If there are no savings but no additional vertices we switch edges with p=1/2. Repeat above steps until no. of vertices is constant. Eliminate all colors whose edges are not isolated. Repeat above steps for remaining graph until no. of vertices is constant. Merge graph obtained. 9/26/2020 27

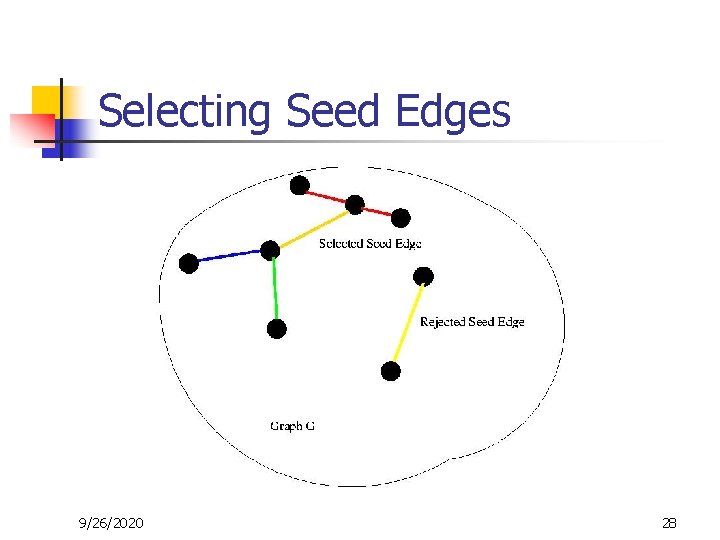
Selecting Seed Edges 9/26/2020 28

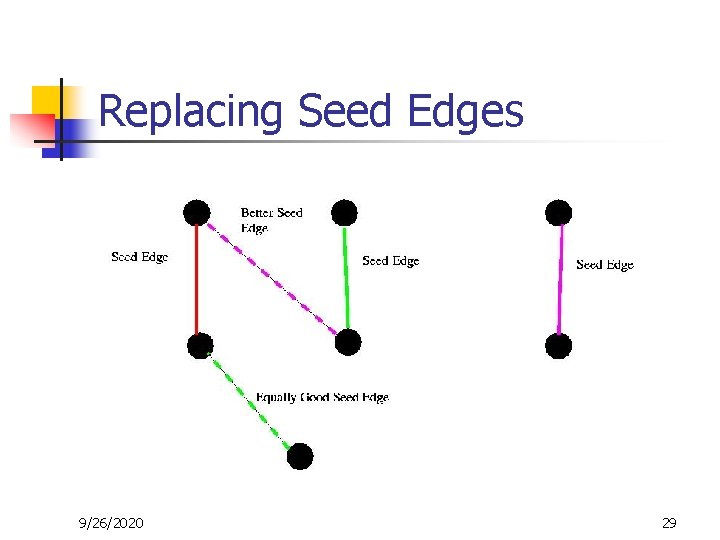
Replacing Seed Edges 9/26/2020 29

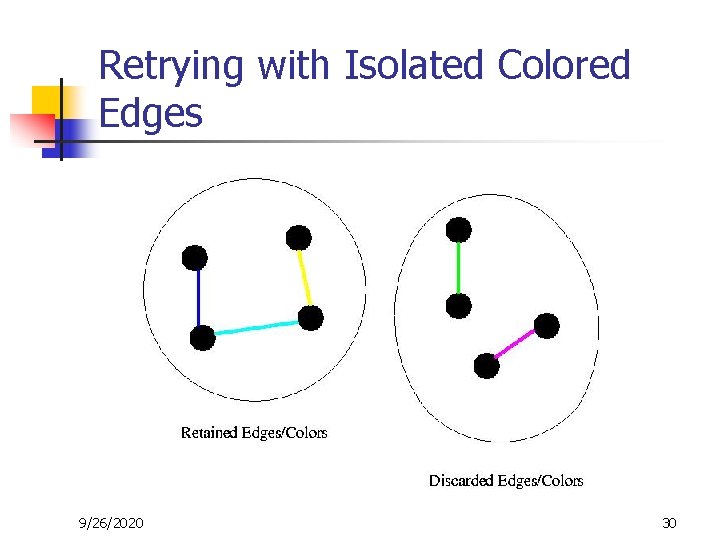
Retrying with Isolated Colored Edges 9/26/2020 30

Preparation of Experimental Data Sets n n n Candidate primer sets for S. Cerevisiae and S. Pombe prepared using Primer 3. Primer length range 8 -12 bases. PCR product size range from 300 -1200 bases. For each gene at most 10, 000 pairs of primers were selected. Three melting temperature ranges for each of S. Cerevisiae and S. Pombe were selected. 9/26/2020 31

Degenerate Data Sets n n n A degenerate primer is a mix of two or more primers usually differing in a small number of bases. Degenerate primers can make resulting colored graph more dense by merging primers. Created degenerate data sets by merging primers differing in at most one base. 9/26/2020 32

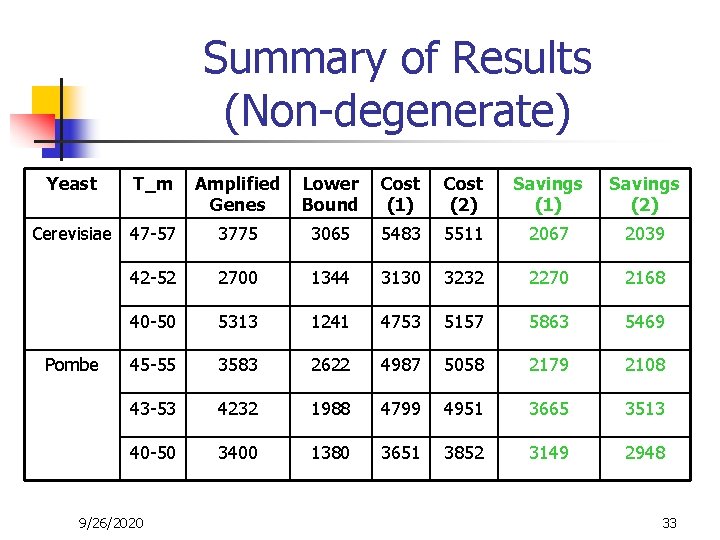
Summary of Results (Non-degenerate) Yeast T_m Amplified Genes Lower Bound Cost (1) Cost (2) Savings (1) Savings (2) Cerevisiae 47 -57 3775 3065 5483 5511 2067 2039 42 -52 2700 1344 3130 3232 2270 2168 40 -50 5313 1241 4753 5157 5863 5469 45 -55 3583 2622 4987 5058 2179 2108 43 -53 4232 1988 4799 4951 3665 3513 40 -50 3400 1380 3651 3852 3149 2948 Pombe 9/26/2020 33

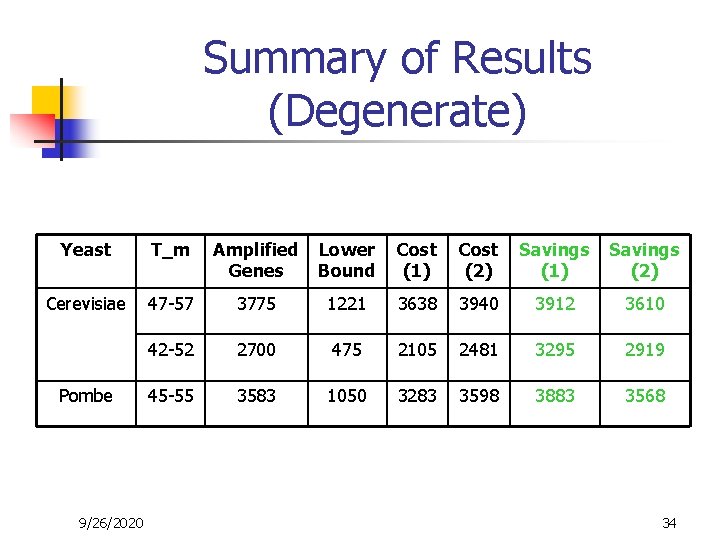
Summary of Results (Degenerate) Yeast T_m Amplified Genes Lower Bound Cost (1) Cost (2) Savings (1) Savings (2) Cerevisiae 47 -57 3775 1221 3638 3940 3912 3610 42 -52 2700 475 2105 2481 3295 2919 45 -55 3583 1050 3283 3598 3883 3568 Pombe 9/26/2020 34

Future Work n n Using longer primers would enable more efficient PCR. Increasing order of degeneracy would give a more dense colored graph and potentially greater savings. Combining the above two ideas is the focus of our current work. Consider the use of existing software architecture to solve other primer design problems. 9/26/2020 35

Acknowledgements n n Thanks to Steven Skiena, Bruce Futcher and Janet Leatherwood. Sponsored by NSF Grant CCR-9988112. 9/26/2020 36