MFGE 404 Computer Integrated Manufacturing CIM ATILIM UNIVERSITY

MFGE 404 Computer Integrated Manufacturing CIM ATILIM UNIVERSITY Manufacturing Engineering Department Lecture 8– Industrial Robots Analysis Fall 2005/2006 Dr. Saleh AMAITIK

Industrial Robot Kinematics • Robot kinematics is concerned with the position and orientation of the robot’s end-of-arm, or the end effector attached to it, as a function of time but without regard for the effects of force or mass. • Our treatment of manipulator kinematics will be limited to the mathematical representation of the position and orientation of the robot’s end-of-arm. • The kinematics analysis involves two different kinds of problems: 1. Determining the coordinates of the end-effector or end-orarm for a given set of joints coordinates (Forward Kinematics), and 2. Determining the joints coordinates for a given location of the end-effector or end-of-arm (Backward Kinematics).

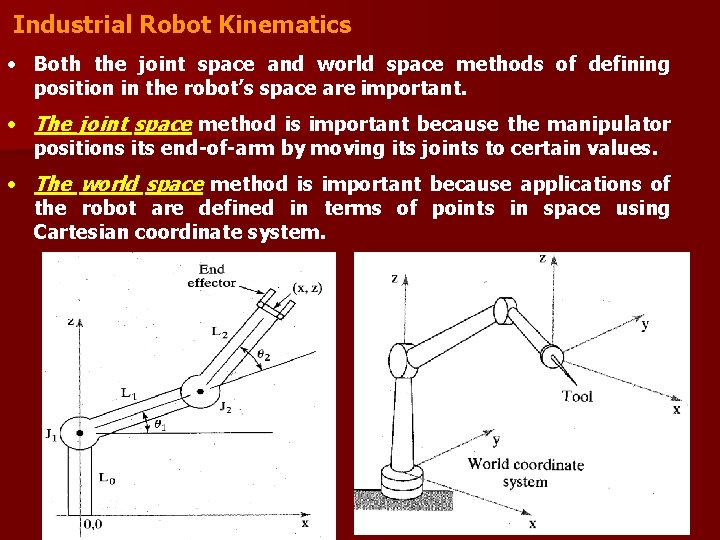
Industrial Robot Kinematics • Both the joint space and world space methods of defining position in the robot’s space are important. • The joint space method is important because the manipulator positions its end-of-arm by moving its joints to certain values. • The world space method is important because applications of the robot are defined in terms of points in space using Cartesian coordinate system.

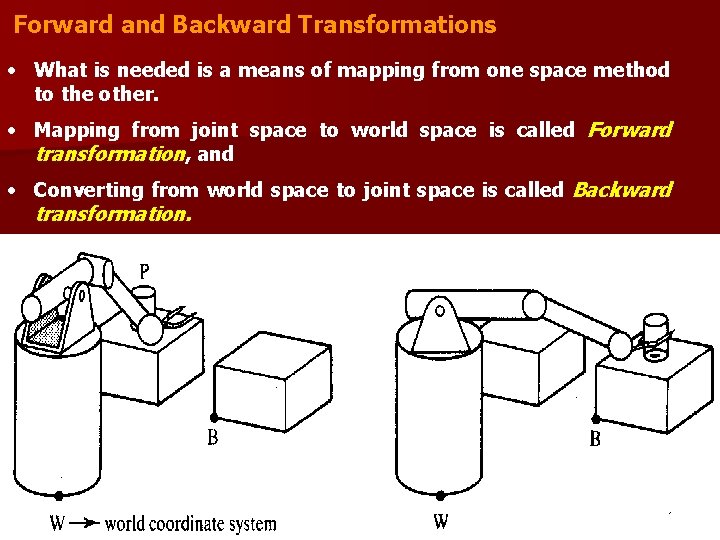
Forward and Backward Transformations • What is needed is a means of mapping from one space method to the other. • Mapping from joint space to world space is called Forward transformation, and • Converting from world space to joint space is called Backward transformation.

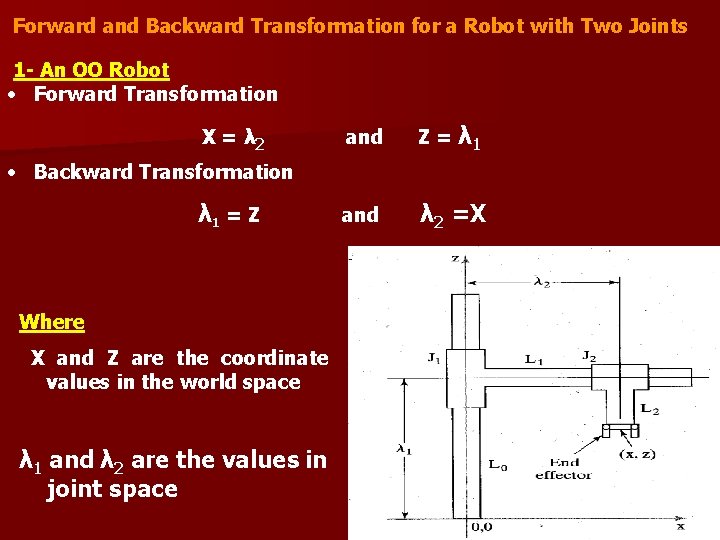
Forward and Backward Transformation for a Robot with Two Joints 1 - An OO Robot • Forward Transformation X = λ 2 and Z = λ 1 and λ 2 =X • Backward Transformation λ 1 = Z Where X and Z are the coordinate values in the world space λ 1 and λ 2 are the values in joint space

Forward and Backward Transformation for a Robot with Two Joints 2 - An RR Robot • Forward Transformation The forward transformation is calculated by noting that the lengths and directions of the two links might be viewed as vectors in space:

Forward and Backward Transformation for a Robot with Two Joints Vector addition or r 1 and r 2 (and taking account of link L 0) yields the coordinate values of X and Z at the end-of-arm:

Forward and Backward Transformation for a Robot with Two Joints • Backward Transformation For the backward transformation, we are given the coordinate positions X and Z in world space, and we must calculate the joint values that will provide those coordinate values.

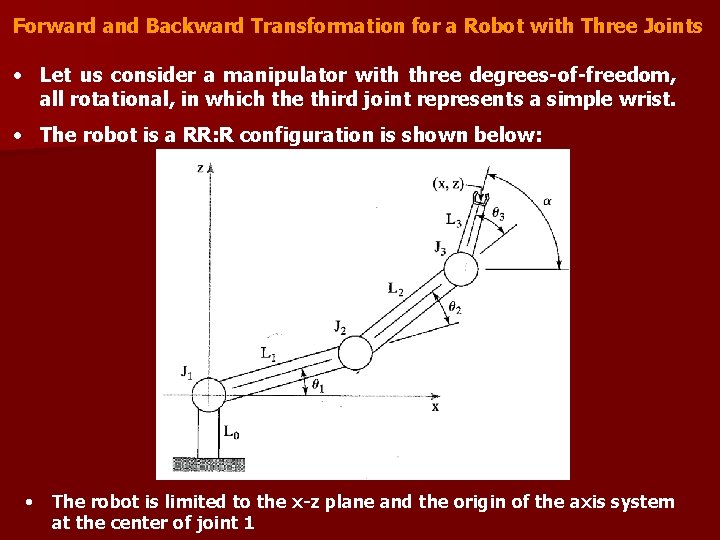
Forward and Backward Transformation for a Robot with Three Joints • Let us consider a manipulator with three degrees-of-freedom, all rotational, in which the third joint represents a simple wrist. • The robot is a RR: R configuration is shown below: • The robot is limited to the x-z plane and the origin of the axis system at the center of joint 1

Forward and Backward Transformation for a Robot with Three Joints • The arm-and-body (RR: ) provides position of the end-of-arm • The wrist (: R) provides orientation. • For the forward transformation, the X and Z coordinates can be calculated as follows: • Let α the orientation angle. It is the angle made by the wrist with the horizontal. It equals the algebraic sum of the three joint angles:

Forward and Backward Transformation for a Robot with Three Joints • In the backward transformation, we are given the world coordinates X, Z, and α, and we want to calculate the joint values θ 1, θ 2 and θ 3 that will achieve those coordinates. • This is accomplished by first determining the coordinates of joint 3 as follows: • Knowing the coordinates of joint 3, the problem of determining θ 1 and θ 2 is as follows: • The value of joint 3 is then determined as

Forward and Backward Transformation for a Robot with Four Joints in Three Dimensions • Consider the four degree-of-freedom configuration is TRL: R. robot shown below. Its • Joint 1 (T type) provides rotation about Z-axis. • Joint 2 (R type) provides rotation about a horizontal axis whose direction is determined by joint 1. • Joint 3 (L Type) is a piston that allows linear motion in a direction determined by joints 1 and 2. • Joint 4 (R type) provides rotation about an axis that is parallel to the axis of joint 2

Forward and Backward Transformation for a Robot with Four Joints in Three Dimensions • The values of the four joints are, respectively, . θ 1, θ 2, λ 3, and θ 4. • Given these values the forward transformation is given by: where

Forward and Backward Transformation for a Robot with Four Joints in Three Dimensions • In the backward transformation, we are given the world coordinates X, Y, Z, and α. Where α specifies orientation. • To find the joint values, we define the coordinates of joint 4 as follows:

Homogenous Transformation • Each of the previous manipulators required its own individual analysis, resulting in its own set of trigonometric equations, to accomplish the forward and backward transformations. • There is a general approach for solving the manipulator kinematics equations based on homogeneous transformations. • The goal in robot motion is often to describe the effect of combined motions resulting from both translation and rotation. • The homogenous transformation approach utilizes vector and matrix algebra to define the joint and link positions and orientations with respect to a fixed coordinate system (world space). • The end-of-arm is defined by the following 4 x 4 matrix:

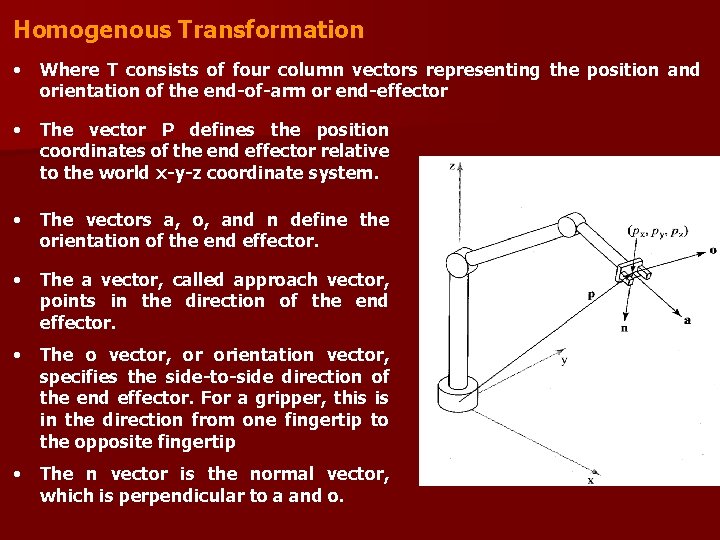
Homogenous Transformation • Where T consists of four column vectors representing the position and orientation of the end-of-arm or end-effector • The vector P defines the position coordinates of the end effector relative to the world x-y-z coordinate system. • The vectors a, o, and n define the orientation of the end effector. • The a vector, called approach vector, points in the direction of the end effector. • The o vector, or orientation vector, specifies the side-to-side direction of the end effector. For a gripper, this is in the direction from one fingertip to the opposite fingertip • The n vector is the normal vector, which is perpendicular to a and o.

Homogenous Transformation • In manipulator kinematics, calculations based on homogeneous transformations are used to establish the geometric relationships among links of the manipulator. • Let A 1 = a 4 x 4 matrix that defines the position and orientation of link 1 with respect to the world coordinate axis. • Similarly, A 2 = a 4 x 4 matrix that defines the position and orientation of the link 2 with respect to link 1. • Then the position and orientation of link 2 with respect to the world coordinate system (called T 2) is given by: T 2 = A 1 A 2 • Where T 2 represents the position and orientation of the end-or-arm (end of link 2) of a manipulator with two joints. • A 1 and A 2 define the changes in position and orientation resulting from the actuations of joints 1 and 2 on links 1 and 2 respectively.

Homogenous Transformation • In general, the position and orientation of the end-of-arm or end-effector can be determined as the product series of homogeneous transformations, usually one transformation for each joint-link combination of the manipulator. • From this matrix, a five degree of freedom manipulator can yield a transformation matrix T = 0 A 5 that specifies the position and orientation of the end point of the manipulator relative to the world coordinate system.