Metrics Unit Conversions Factor Label Method 1 Write

Metrics- Unit Conversions Factor Label Method 1. Write the given number and unit. (Convert 12 cm to meters. ) 2. Set up a conversion (1 m = 100 cm) a. Place the given unit as denominator of conversion factor. 1) Conversion factors are simple ratios. b. Place desired unit as numerator. c. Place a “ 1” in front of the larger unit. (m vs. cm) d. Determine the number of smaller units needed to make “ 1” of the larger unit. Place it with the applicable unit. 1 m 12 Solve cm the problem. 3. Cancel units. X 100 cm = 0. 12 m

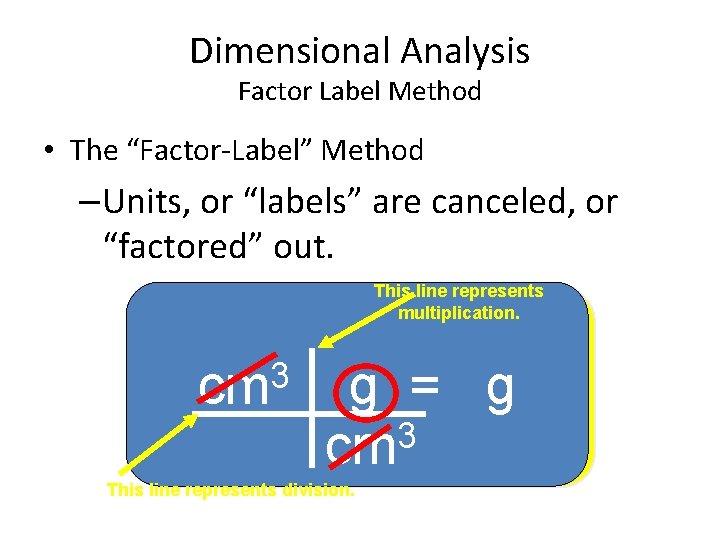
Dimensional Analysis Factor Label Method • The “Factor-Label” Method –Units, or “labels” are canceled, or “factored” out. This line represents multiplication. 3 cm 1 g = g g 3 cm This line represents division.

Dimensional Analysis • Lining up conversion factors (What is a conversion factor): 1 in = 2. 54 cm =1 2. 54 cm 1 in = 2. 54 cm 1= 1 in

Dimensional Analysis Factor Label Method 1. Write the given number and unit. Convert 24. 2 inches to centimeters. 2. Set up a conversion factor. 1 inch = 2. 54 cm a. Place the given unit as denominator of conversion factor. 1) Conversion factors are simple ratios. b. Place desired unit as numerator. c. Place the applicable values with the corresponding units. 3. Cancel units. Solve the problem. 24. 2 in. X 2. 54 cm _______ 1 in. = 61. 5 cm

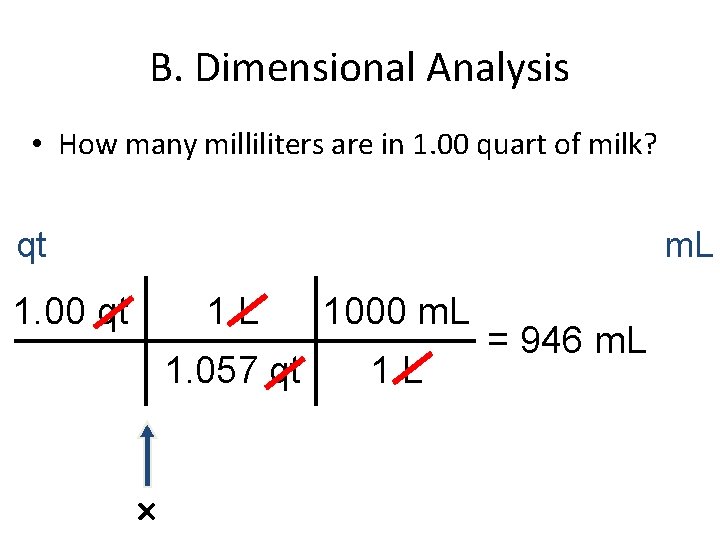
B. Dimensional Analysis • How many milliliters are in 1. 00 quart of milk? qt m. L 1. 00 qt 1 L 1000 m. L 1. 057 qt 1 L = 946 m. L

B. Dimensional Analysis • You have 1. 5 pounds of gold. Find its volume in cm 3 if the density of gold is 19. 3 g/cm 3. lb cm 3 1. 5 lb 1 kg 1000 g 1 cm 3 2. 2 lb 1 kg 19. 3 g = 35 cm 3

B. Dimensional Analysis • How many liters of water would fill a container that measures 75. 0 in 3? in 3 L 75. 0 in 3 (2. 54 cm)3 (1 in)3 1 L 1000 cm 3 = 1. 23 L

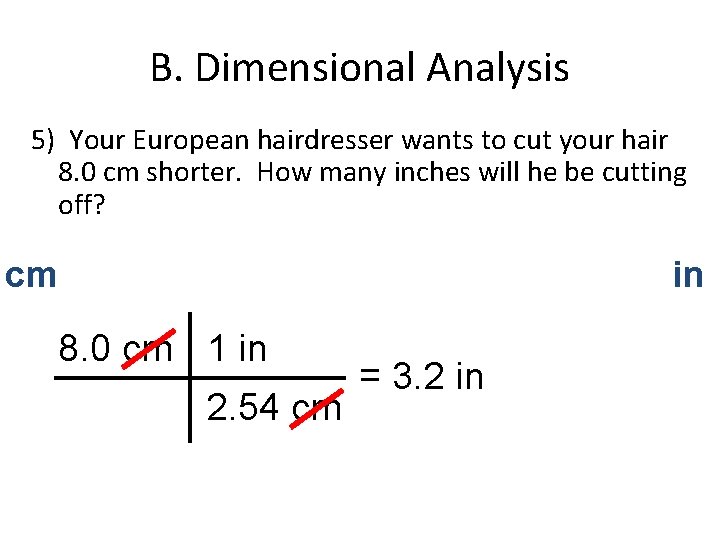
B. Dimensional Analysis 5) Your European hairdresser wants to cut your hair 8. 0 cm shorter. How many inches will he be cutting off? cm in 8. 0 cm 1 in 2. 54 cm = 3. 2 in

B. Dimensional Analysis 6) Taft football needs 550 cm for a 1 st down. How many yards is this? cm 550 cm yd 1 in 1 ft 1 yd 2. 54 cm 12 in 3 ft = 6. 0 yd

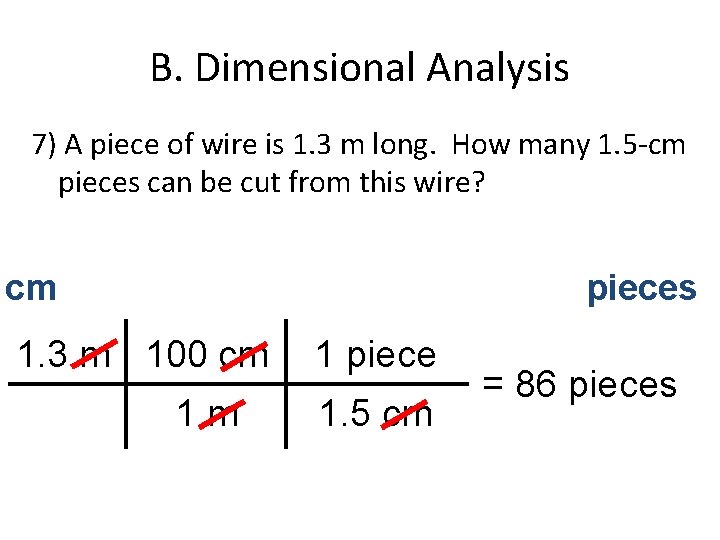
B. Dimensional Analysis 7) A piece of wire is 1. 3 m long. How many 1. 5 -cm pieces can be cut from this wire? cm pieces 1. 3 m 100 cm 1 m 1 piece 1. 5 cm = 86 pieces

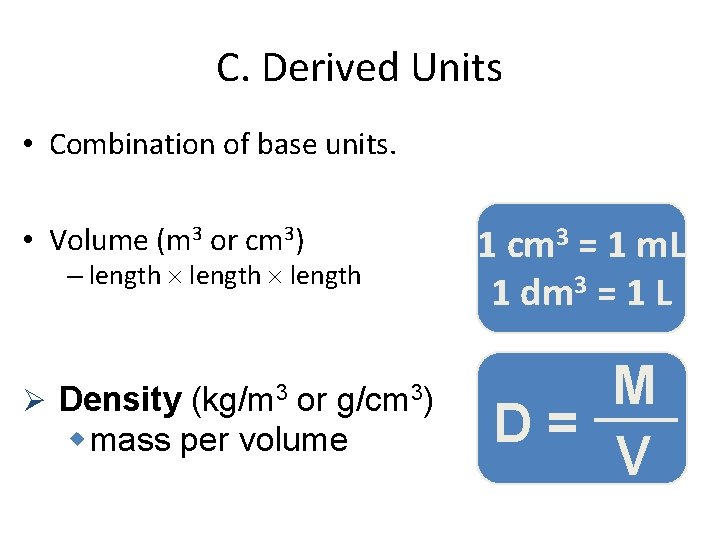
C. Derived Units • Combination of base units. • Volume (m 3 or cm 3) – length Ø Density (kg/m 3 or g/cm 3) w mass per volume 1 cm 3 = 1 m. L 1 dm 3 = 1 L M D= V

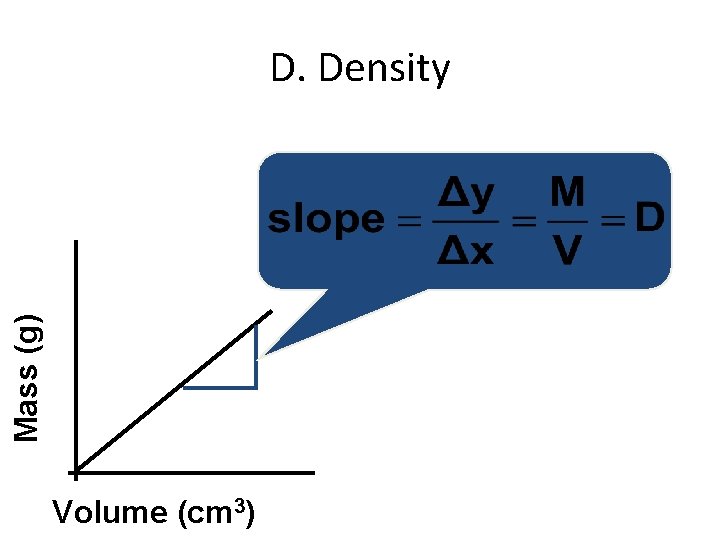
Mass (g) D. Density Volume (cm 3)

Problem-Solving Steps 1. Analyze 2. Plan 3. Compute 4. Evaluate