METRIC SYSTEM It is the decimal measuring system

METRIC SYSTEM It is the decimal measuring system based on the meter, liter, and gram as units of length, volume, and weight or mass. The system was first proposed by the French astronomer and mathematician Gabriel Mouton (1618– 94) in 1670 and was standardized in France under the Republican government in the 1790 s. © Copyright 2003 - 2004. M. J. Krech. All rights reserved.

The Metric System is based on sets of 10. 1 x 10 = 10 10 X 10 = 100 10 x 100 = 1, 000

Do you remember… King Henry?

The pneumonic: King Henry Died Unexpectedly Drinking Chocolate Milk Memorize this!

King k kilo 1000 Henry h hecto 100 Died da deca 10 Unexpectedly base unit (meter, liter, gram) Drinking d deci 0. 1 (1/10) Chocolate c centi 0. 01 (1/100) Milk m milli 0. 001 (1/1000)

You must also know… …how to convert within the Metric System. Here’s a good device: On your paper draw a line and add 7 tick marks:

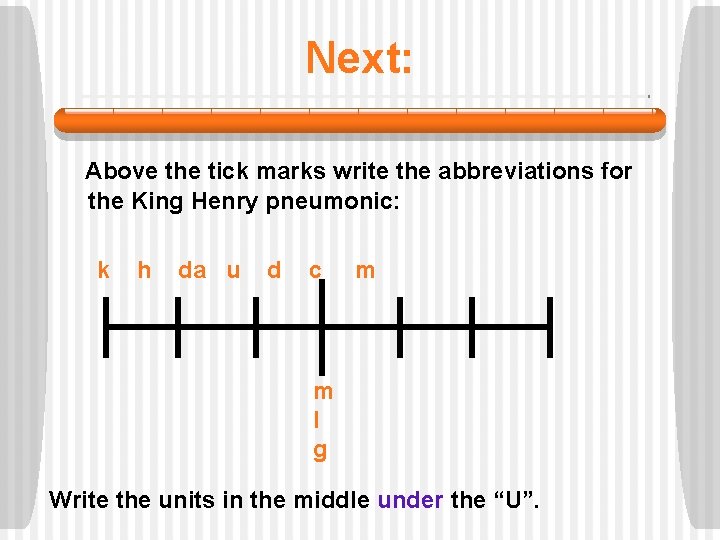
Next: Above the tick marks write the abbreviations for the King Henry pneumonic: k h da u d c m m l g Write the units in the middle under the “U”.

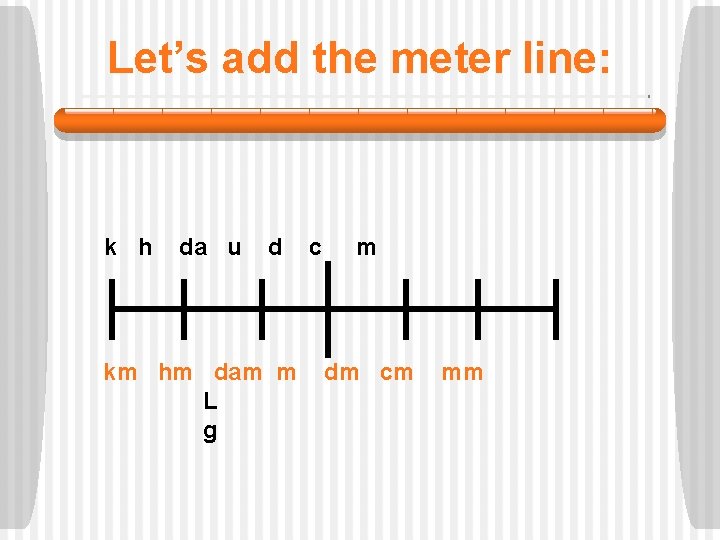
Let’s add the meter line: k h da u d km hm dam m L g c m dm cm mm

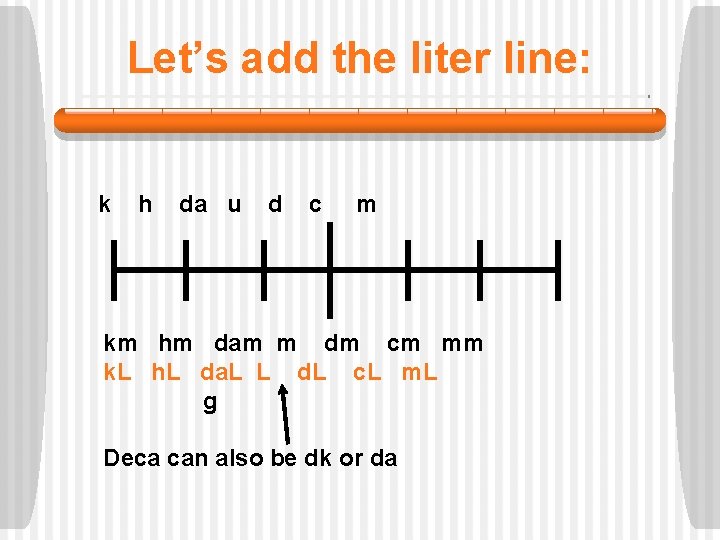
Let’s add the liter line: k h da u d c m km hm dam m dm cm mm k. L h. L da. L L d. L c. L m. L g Deca can also be dk or da

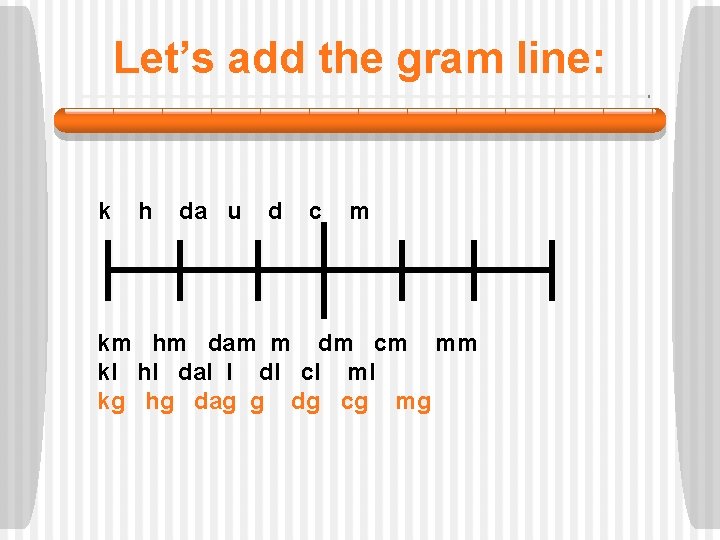
Let’s add the gram line: k h da u d c m km hm dam m dm cm mm kl hl dal l dl cl ml kg hg dag g dg cg mg

How to use this device: 1. Look at the problem. Look at the unit that has a number. On the device put your pencil on that unit. 2. Move to new unit, counting jumps and noticing the direction of the jump. 3. Move decimal in original number the same # of spaces and in the same direction.

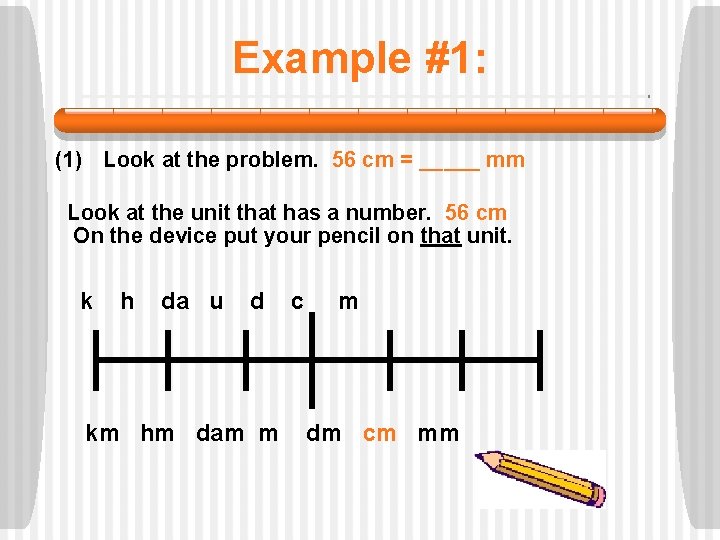
Example #1: (1) Look at the problem. 56 cm = _____ mm Look at the unit that has a number. 56 cm On the device put your pencil on that unit. k h da u d km hm dam m c m dm cm mm

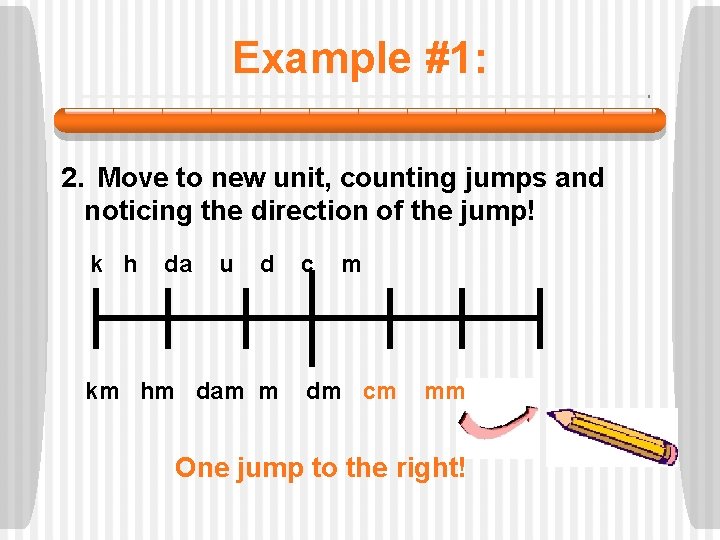
Example #1: 2. Move to new unit, counting jumps and noticing the direction of the jump! k h da u d km hm dam m c m dm cm mm One jump to the right!

Example #1: 3. Move decimal in original number the same # of spaces and in the same direction. 56 cm = _____ mm 56. 0. One jump to the right! Move decimal one jump to the right. Add a zero as a placeholder.

Example #1: 56 cm = _____ mm 56 cm = 560 mm

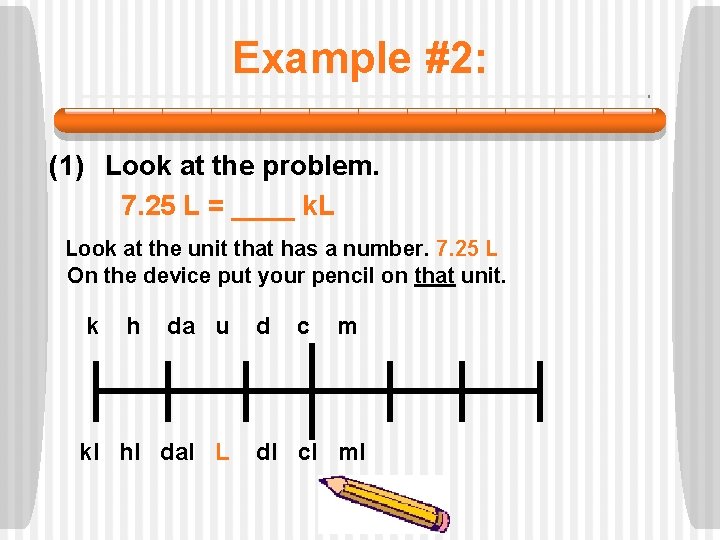
Example #2: (1) Look at the problem. 7. 25 L = ____ k. L Look at the unit that has a number. 7. 25 L On the device put your pencil on that unit. k h da u kl hl dal L d c m dl cl ml

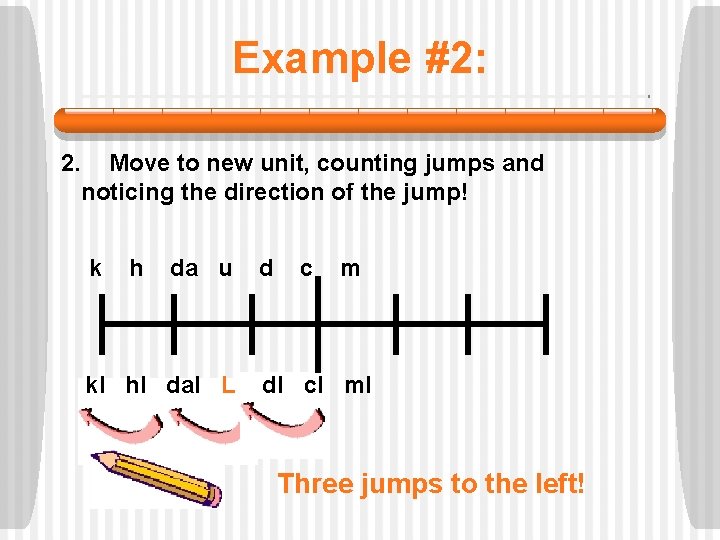
Example #2: 2. Move to new unit, counting jumps and noticing the direction of the jump! k h da u kl hl dal L d c m dl cl ml Three jumps to the left!

Example #2: (3) Move decimal in original number the same # of spaces and in the same 7. 25 L = ____ k. L . 007. 25 Three jumps to the left! Move decimal to the left three jumps. Add two zeros as placeholders. direction.

Example #2: 7. 25 L = ____ k. L 7. 25 L =. 00725 k. L

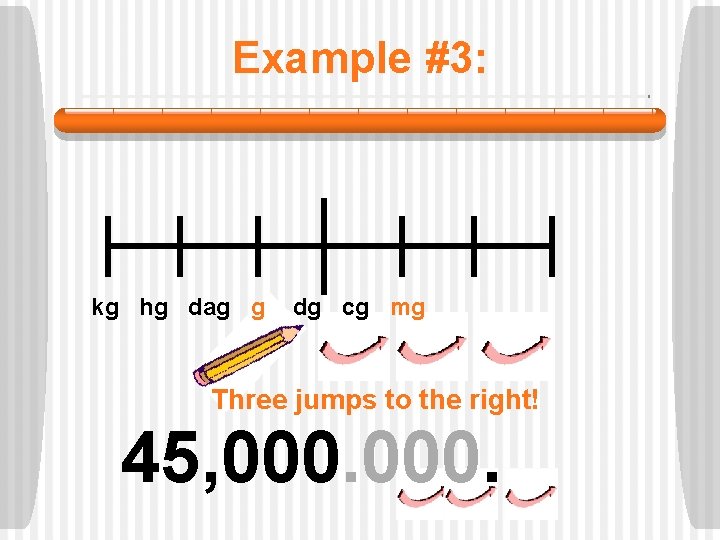
Example #3: Try this problem on your own: 45, 000 g = ____mg kg hg dag g dg cg mg

Example #3: kg hg dag g dg cg mg Three jumps to the right! 45, 000.

Example #3: 45, 000 g = 45, 000 mg Three jumps to the right!

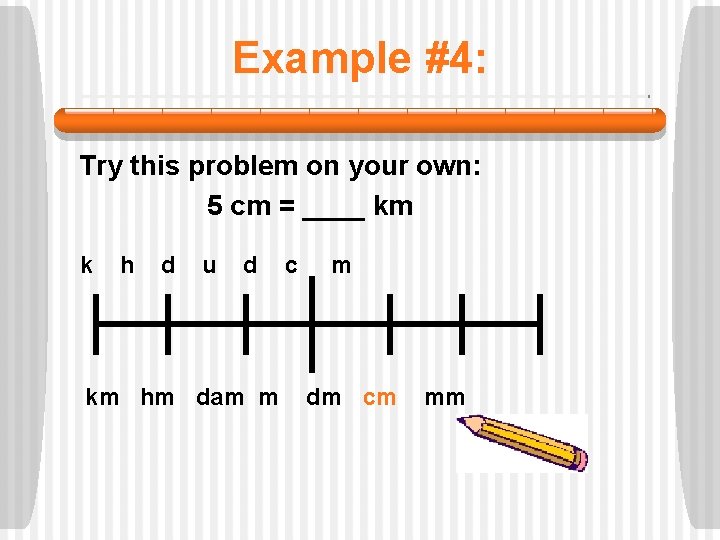
Example #4: Try this problem on your own: 5 cm = ____ km k h d u d km hm dam m c m dm cm mm

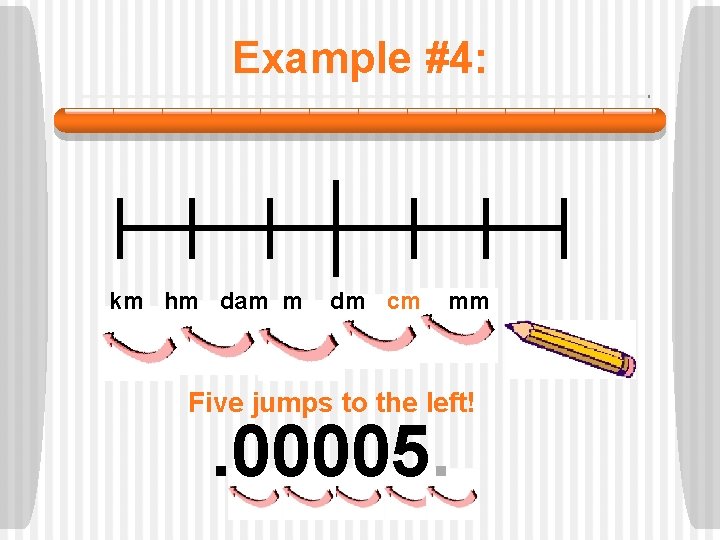
Example #4: km hm dam m dm cm mm Five jumps to the left! . 00005.

Example #4: 5 cm =. 00005 km Five jumps to the left!

Examples #5 -9: Solve these five problems on your own.

Examples #5 -9: (5) 35 mm = ____ cm (6) 14, 443 L = ____ k. L (7) 0. 00056 kg = ____ g (8)35. 4 L = ____ m. L (9)16 mm = ____ km

One last caution: Be careful NOT to count the spot you start from, where you put your pencil point. Only count the jumps!

The End