Metric System and Significant Figures The Metric System

Metric System and Significant Figures

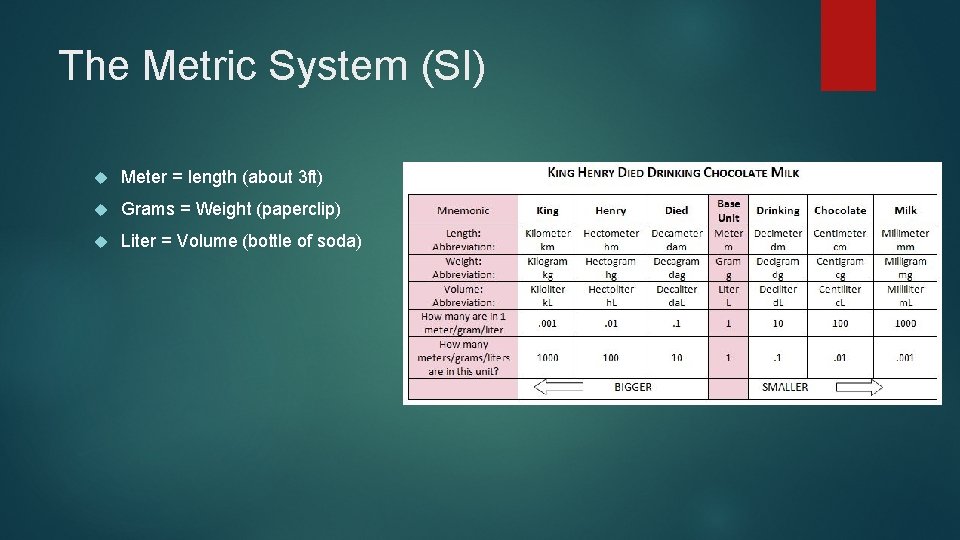
The Metric System (SI) Meter = length (about 3 ft) Grams = Weight (paperclip) Liter = Volume (bottle of soda)

Significant Figures What is the point of significant figures? When you are measuring something, significant figures are used to show precise you measured too. Examples 0. 00600 0. 073 270. 10. 0 705. 001 37, 000

Rules of Significant Figures Count any non 0 digits and zeros in between 2005. 705. 001 Rule out leading 0 s (The zeros that come before your non-zero digit 0. 006 00. 0679 LEADING 0 s NOT SIGNIFICANT Trailing 0 s If you have a decimal anywhere in your number count the trailing 0 s 0. 6000 If you do not have a decimal, it is too ambiguous, 67, 000 700

Identifying Significant Figures 1. 0. 001 2. 4. 006 3. 500 4. 0. 0245 5. 70. 6. 2398 7. 2000 8. 0. 00054 9. 24. 0076 10. 0. 870

Adding and Subtraction When adding and subtracting precise measurements significant figures don’t matter as much, as the actual precision of what you are measuring 1. 26 + 2. 3 =3. 56 Go by the least precise thing you measured 2. 3 (2 sig fig) round 3. 56 to 3. 6 1. 26 + 102. 3 = 103. 56 Precision is the amount of numbers after the decimal point (not the actual significant digits 103. 56 103. 6

Adding and Subtraction Why do we forget about sig fig and only look at the numbers after the decimal point? Block 1 2. 09 m Block 2 1. 901 m 2. 09 m + 1. 901 m =3. 991 m Because we measured to the hundredth on the 1 st block and measured to the thousandth on the 2 nd block we can only write to the hundredth spot 3. 991 rounds to 3. 99

Adding and Subtraction This does not only apply when there is a decimal point Building 450 ft Antenna 8 ft 450+8 = 458 However we were only able to measure the building precisely to the tens spot 458 rounds to 460 ft 45. 01 + 6. 2 6. 002 + 8. 03 60 + 6 624 + 2 4. 5 + 2. 3 3. 02 +6. 1

Multiplying and Dividing Measuring carpet Setting down tile in your kitchen 2. 03 m x 3. 06 m = 6. 2118 m^2 Area of kitchen 6. 2118 rounds to 6. 21 m^2 because we were only able to measure to the centimeter. 12. 07 ft x 10. 1 ft = 121. 907 ft (Area) 3 sig fig 122 However, we are not done with our math When multiplying and dividing use the least significant figure out of your two numbers that you are multiplying Tile area (1. 07 ft) Do not round until you are done with your math 121. 907/1. 07 = 113. 931775… Now we care about sig fig 113. 931775. . 114 ft^2

Multiplying and dividing 1. 346. 3 x 24. 7 2. 10. 001 x 24. 3 3. 80. /20. 4. 373 x 2 5. 940/10 6. 24. x 35 7. 78. /2. 01 8. 863. 01/24. 003 9. 845 x 2. 01 10. 7. 0 x 208.