Metody numeryczne SOWIG Wydzia Inynierii rodowiska III rok

Metody numeryczne SOWIG Wydział Inżynierii Środowiska III rok dr inż. Jerzy Kotowski Instytut Informatyki, Automatyki i Robotyki

Metody numeryczne Aproksymacja dr inż. Jerzy Kotowski Instytut Informatyki, Automatyki i Robotyki

Aproksymacja Definicje • Aproksymacja jest to zastępowanie jednych wielkości innymi, bliskimi w ściśle sprecyzowanym sensie. W skrócie: przybliżenie jednej wartości za pomocą innych. • Aproksymowaniem funkcji nazywamy przybliżanie jej za pomocą kombinacji liniowej tzw. funkcji bazowych. • Funkcja aproksymująca – przybliżenie zadanej funkcji nie musi przechodzić przez jakieś zadane punkty, tak jak to jest w interpolacji. • Dużą zaletą aproksymacji w stosunku do interpolacji jest to, że aby dobrze przybliżać, funkcja aproksymująca nie musi być wielomianem bardzo dużego stopnia. • Przybliżanie (aproksymacja) powoduje pojawienie się błędów, zwanych błędami aproksymacji. (Wikipedia) • Najczęściej aproksymacja jest to przybliżanie funkcji f(x) zwanej funkcją aproksymowaną inną funkcją Q(x) zwaną funkcją aproksymującą.

Aproksymacja Definicje • Aproksymacja bardzo często występuje w dwóch przypadkach: – gdy funkcja aproksymowana jest przedstawiona w postaci tablicy wartości i poszukujemy dla niej odpowiedniej funkcji ciągłej lub – gdy funkcję o dosyć skomplikowanym zapisie analitycznym chcemy przedstawić w „prostszej” postaci. • Dokonując aproksymacji funkcji musimy rozwiązać dwa ważne problemy. A Dobór odpowiedniej funkcji aproksymującej Q(x). Najczęściej będzie to tzw. wielomian uogólniony będący kombinacją liniową funkcji bazowych qi(x), i=0, 2, …, m. B Określenie dokładności dokonanej aproksymacji. Aproksymacja funkcji powoduje powstanie błędów i sposób ich oszacowania wpływa na wybór metody aproksymacji. • Istnieje wiele sposobów aproksymacji. Jednymi z najbardziej popularnych są aproksymacja średniokwadratowa i aproksymacja jednostajna oraz aproksymacja liniowa.

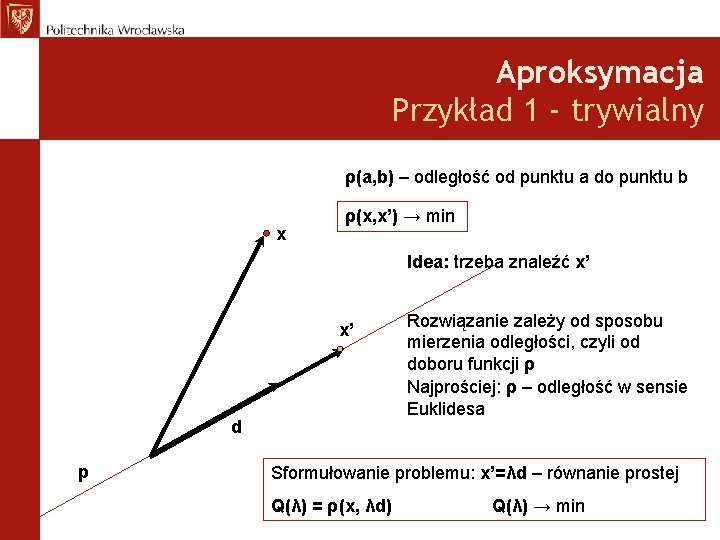
Aproksymacja Przykład 1 - trywialny ρ(a, b) – odległość od punktu a do punktu b x ρ(x, x’) → min Idea: trzeba znaleźć x’ x’ d p Rozwiązanie zależy od sposobu mierzenia odległości, czyli od doboru funkcji ρ Najprościej: ρ – odległość w sensie Euklidesa Sformułowanie problemu: x’=λd – równanie prostej Q(λ) = ρ(x, λd) Q(λ) → min

Aproksymacja Metryki • Metryka == odległość == długość najkrótszej drogi • Własności metryki a, b A – ρ(a, b)= ρ(b, a) – ρ(a, b)=0 a=b – ρ(a, b) ρ(a, c)+ ρ(c, b) nierówność trójkąta • Najgłupsza metryka: – a=b ρ(a, b)=0 – a b ρ(a, b)=1 • Założenie a, b Rk • Ważne metryki: – Metryka taksówkowa – Metryka euklidesowa – Metryka maksimum

Aproksymacja Metryki Metryka taksówkowa – jeździmy po Nowym Jorku y 2 y Ogólnie: x 2 x x 1 y 1 Metryka == długość najkrótszej drogi

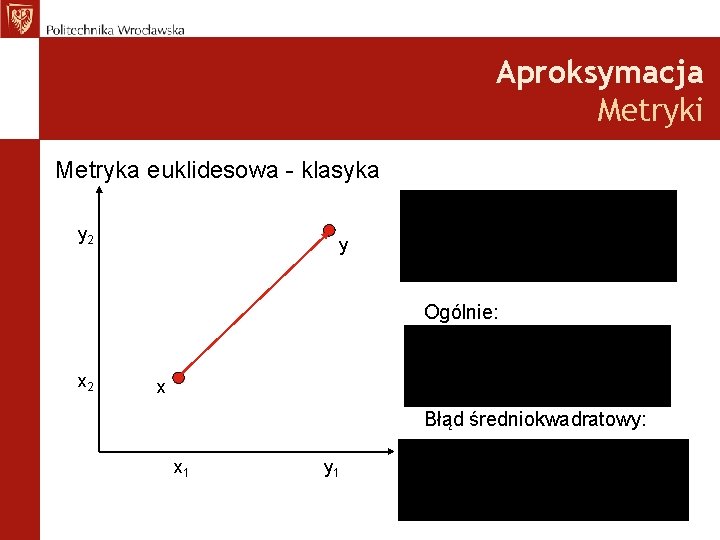
Aproksymacja Metryki Metryka euklidesowa - klasyka y 2 y Ogólnie: x 2 x Błąd średniokwadratowy: x 1 y 1

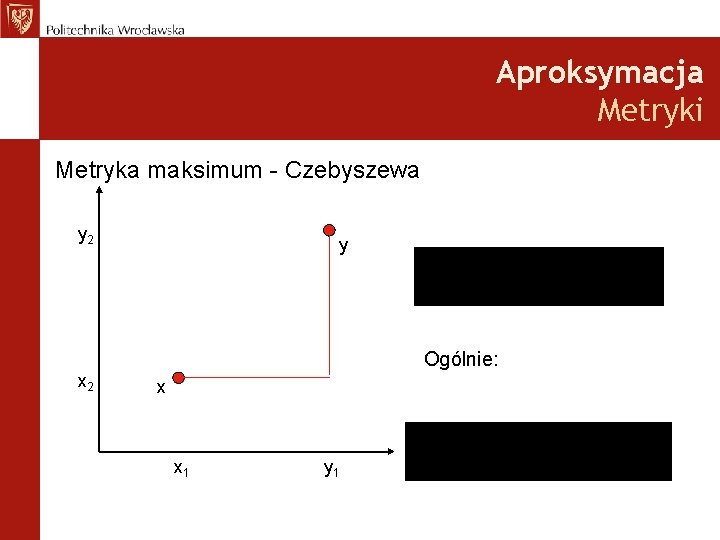
Aproksymacja Metryki Metryka maksimum - Czebyszewa y 2 y Ogólnie: x 2 x x 1 y 1

Aproksymacja Metryki • Wybór metryki zależy od natury problemu. • Bardzo często wypadałoby stosować metrykę maksimum. • Przykład: Prowadzimy samochód. Mamy trajektorię zadaną i trasę, którą my nakreśliliśmy na powierzchni planety. • Miarą jakości naszej jazdy jest największe odchylenie od zalecanego kursu -> metryka maksimum. Staramy się tak jechać aby wartość tej miary jakości była jak najmniejsza. • MINIMAX. • Niestety, metryka maksimum prowadzi do problemów bardzo trudnych obliczeniowo. • Dlatego, chcąc – nie chcąc, korzystamy często z metryki euklidesowej. • Czasami nie ma to sensu i może być tragiczne w skutkach. • Minimalizując błąd średniokwadratowy możemy znaleźć się w rowie. Średnio może być bardzo dobrze ale jeden wyskok, który nie zmieni bardzo średniej może być fatalny w skutkach.

Aproksymacja Identyfikacja • Aproksymacja == Identyfikacja i 1 2 … k • Seria pomiarowa • Przykład: x x 1 x 2 … xk Zmierzyliśmy k razy długość stołu • Chcemy wypowiedzieć się na temat , tzn. rzeczywistej, obiektywnie istniejącej długości tego obiektu. • Błędy pomiaru: ei=xi- , i=1, 2, …, k. • Wektor błędów pomiaru e=(e 1, e 2, …, ek)T Rk. • Intuicja: chcemy tak dobrać , aby wektor e był jak najmniejszy (najkrótszy). • Czyli aby odległość od e do początku układu współrzędnych 0=(0, 0, …, 0)T była jak najmniejsza: e = ρ(e, 0) min • Wektor e zależy od poszukiwanego : e=e( ) Q( )= e( ) min

Aproksymacja Przykład z życia • Na pewnej uczelni wyższej grupa k osób (być może k=16) wysłuchała niesamowicie ciekawego referatu o obiektowo zorientowanych językach programowania na laboratorium z Metod Numerycznych. • Wszyscy chcą wiedzieć ile to wystąpienie było naprawdę warte. • Głosowanie dało dane pomiarowe na potrzeby identyfikacji. Na rysunku dane te zostały już posortowane. e 15 0 x 1 x 2 x 3 x 4 …… • Minimax (metryka maksimum): max |ei| min • opt=0. 5(x 1+x 16). • Metryka euklidesowa: x 15 x 16

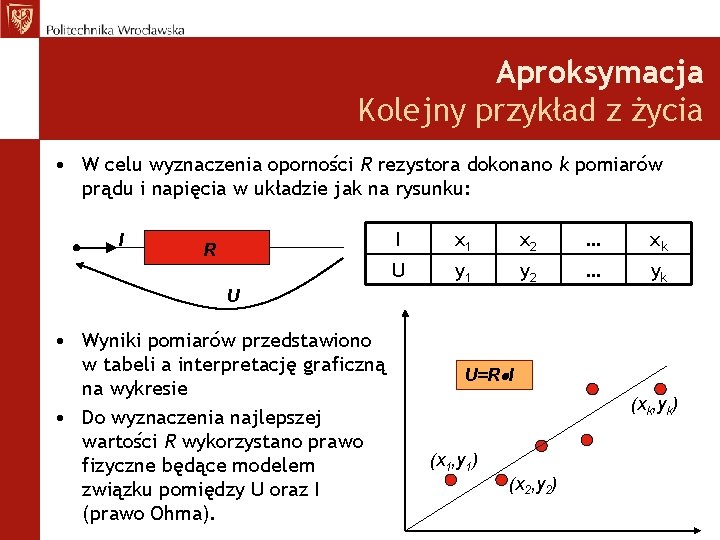
Aproksymacja Kolejny przykład z życia • W celu wyznaczenia oporności R rezystora dokonano k pomiarów prądu i napięcia w układzie jak na rysunku: I R I x 1 x 2 … xk U y 1 y 2 … yk U • Wyniki pomiarów przedstawiono w tabeli a interpretację graficzną na wykresie • Do wyznaczenia najlepszej wartości R wykorzystano prawo fizyczne będące modelem związku pomiędzy U oraz I (prawo Ohma). U=R I (xk, yk) (x 1, y 1) (x 2, y 2)

Aproksymacja Identyfikacja parametryczna • Związek pomiędzy interesującymi nas zmiennymi znamy z teorii (fizyka, chemia, ekonomia, etc. ): y=f(x, ). • Identyfikacja obiektu polega na wyznaczeniu WEKTORA nieznanych parametrów w oparciu o serię danych pomiarowych. • Seria pomiarowa ma długość k. • Wektor ma n składowych. • W przykładzie z opornikiem n=1. • Idea rozumowania: gdyby nie było błędów pomiarów i gdyby prawo Ohma idealnie odzwierciedlało rzeczywistość to wtedy powinno istnieć takie (tzn. R), że yi= xi, i=1, 2, …, k. Prawdopodobnie tak nie będzie. Dlatego budujemy wektor błędów o składowych ei=yi- xi • Dobieramy parametr , tak aby wektor błędów e miał najmniejszą długość w metryce euklidesowej.

Aproksymacja Rozwiązanie problemu Zawsze istnieje rozwiązanie!!

Aproksymacja Model matematyczny obiektu • • • Model matematyczny obiektu na potrzeby identyfikacji Związek pomiędzy wejściem i wyjściem obiektu Czarna skrzynka y x – wejście x y=f(x, ) y – wyjście xi – pomiary na wejściu obiektu yi – pomiary na wyjściu obiektu Terminy wejście i wyjście nie muszą mieć odniesienia praktycznego. Często zdarza się, że fizyczne wejście obiektu z punktu widzenia modelu matematycznego na potrzeby identyfikacji jest wyjściem i odwrotnie.

Aproksymacja Zapis wektorowy (A+B)T=AT+BT (AB)T=BTAT ATT=A (A+B)C=AC+BC a. A=Aa

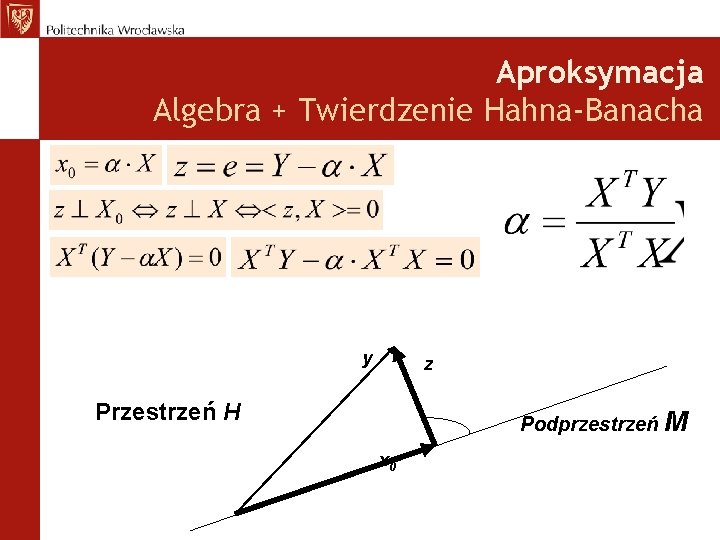
Aproksymacja Twierdzenie Hahna-Banacha T w i e r d z e n i e (o rzucie ortogonalnym) Niech M będzie podprzestrzenią liniową domkniętą przestrzeni Hilberta H. Wtedy każdy element y H da się przedstawić w postaci y=x 0+z, gdzie x 0 M, z M, przy czym rozkład ten jest jednoznaczny. Element x 0 nazywa się rzutem ortogonalnym elementu y na podprzestrzeń M. y z Przestrzeń H Podprzestrzeń M x 0

Aproksymacja Algebra + Twierdzenie Hahna-Banacha y z Przestrzeń H Podprzestrzeń M x 0

Aproksymacja Model matematyczny – trochę ogólniej • Przypadek ogólniejszy – obiekt posiada n wejść • Model matematyczny obiektu: x x 1 x 2 xn • Model obiektu jest liniową zależnością ze względu na x oraz • Seria pomiarowa • X – macierz pomiarów na w. Ejściu • Y – macierz pomiarów na w. Yjściu • X=Xkn , Y=Yk y=f(x, ) y y

Aproksymacja Zapis wektorowy - ogólnie

Aproksymacja Funkcja wielu zmiennych Funkcja Q( ) jest funkcją n zmiennych Wartości funkcji Q( ) są liczbami rzeczywistymi G – macierz Grama. Własność 1: Własność 2: Macierz Grama jest macierzą symetryczną i półdodatniokreśloną Szukamy minimum funkcji

Aproksymacja Układ równań liniowych Problem wyznaczenia najlepszej aproksymacji obiektu liniowego o n wejściach sprowadza się do rozwiązania układu n równań liniowych z n niewiadomymi. Układ ten ma zawsze rozwiązanie. Czasami rozwiązań jest nieskończenie wiele.

Aproksymacja Twierdzenie Hahna-Banacha ogólnie Podprzestrzeń M rozpięta na kolumnach macierzy X Wektor błędu aproksymacji Twierdzenie Hahna-Banacha To znaczy: Można to zapisać krócej: Albo:

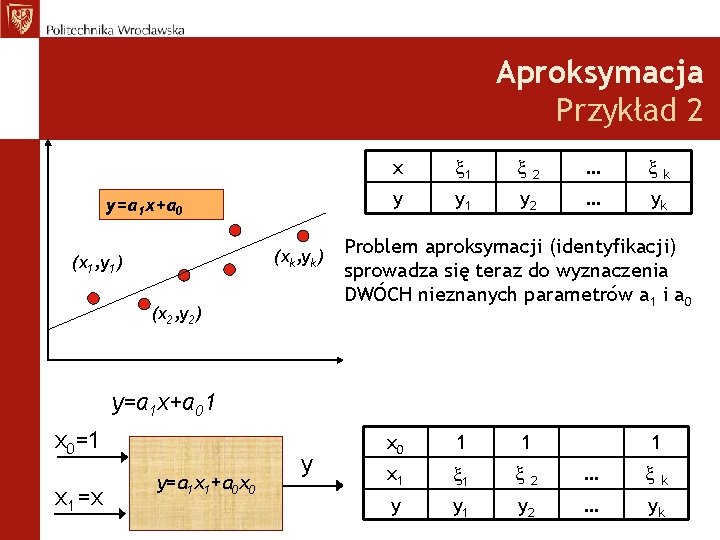
Aproksymacja Przykład 2 y=a 1 x+a 0 (xk, yk) (x 1, y 1) (x 2, y 2) x 1 2 … y y 1 y 2 … yk k Problem aproksymacji (identyfikacji) sprowadza się teraz do wyznaczenia DWÓCH nieznanych parametrów a 1 i a 0 y=a 1 x+a 01 x 0=1 x 1 =x y=a 1 x 1+a 0 x 0 y x 0 1 1 1 x 1 1 2 … y y 1 y 2 … yk k

Aproksymacja Przykład 2

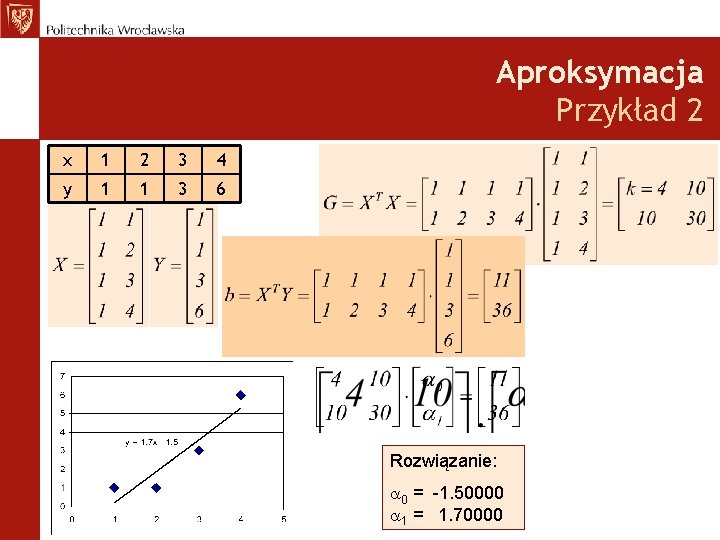
Aproksymacja Przykład 2 x 1 2 3 4 y 1 1 3 6 Rozwiązanie: 0 = -1. 50000 1 = 1. 70000

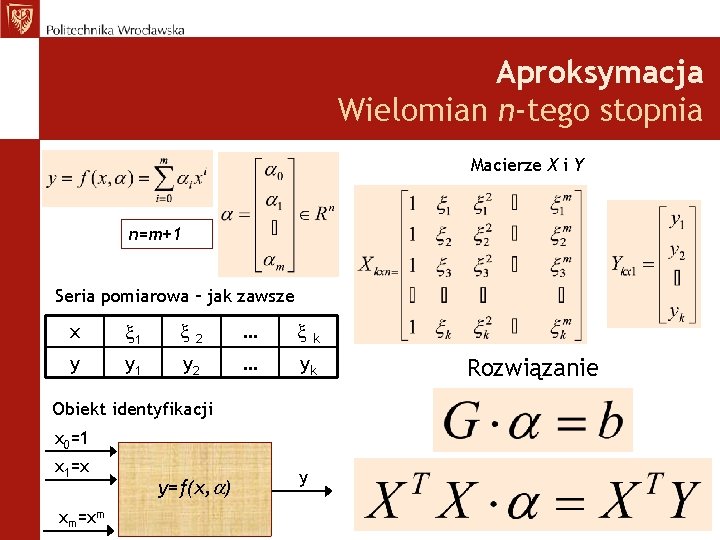
Aproksymacja Wielomian n-tego stopnia Macierze X i Y n=m+1 Seria pomiarowa – jak zawsze x 1 2 … y y 1 y 2 … yk Obiekt identyfikacji x 0=1 x 1=x xm=xm y=f(x, ) y k Rozwiązanie

Aproksymacja Uogólniony wielomian n-tego stopnia Macierze X i Y n=m+1 Seria pomiarowa – jak zawsze x 1 2 … y y 1 y 2 … yk Obiekt identyfikacji x 0=1 =q 0(x) x 1=x =q 1(x) =xm xm=q m(x) y=f(x, ) y k Rozwiązanie

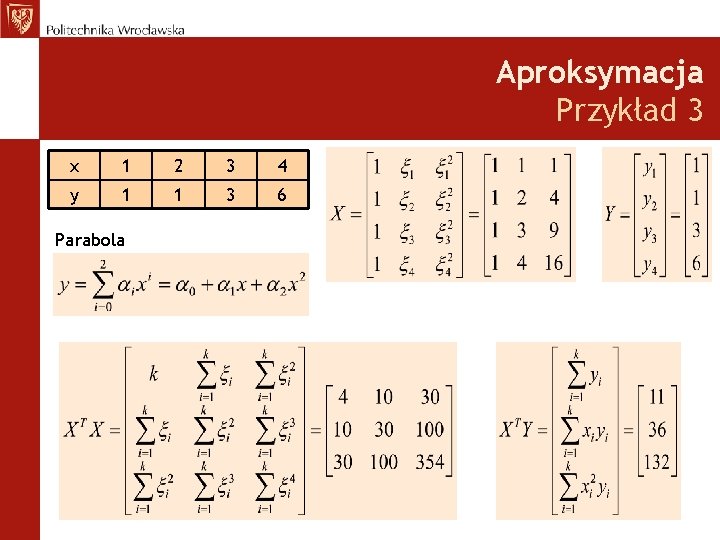
Aproksymacja Przykład 3 x 1 2 3 4 y 1 1 3 6 Parabola

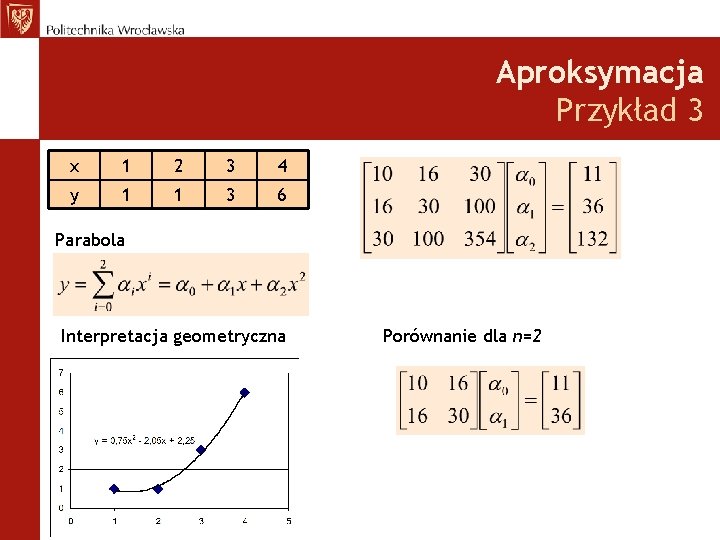
Aproksymacja Przykład 3 x 1 2 3 4 y 1 1 3 6 Parabola Interpretacja geometryczna Porównanie dla n=2

Aproksymacja Wnioski • Przedstawione postępowanie jest możliwe do przeprowadzenia jeżeli tylko model matematyczny identyfikowanego obiektu y=f(x, ) jest liniową funkcją parametrów . • Taka funkcja nosi nazwę uogólnionego wielomianu. • Przykłady uogólnionych wielomianów: – Klasyczny wielomian: y=a 2 x 2+a 1 x+a 0 – Rozwiązania liniowych równań różniczkowych czyli wyrażenia typu: y=a 1 exsin(x)+a 2 excos(x)+a 3 • Przykład zależności nieliniowej: y=e xsin( x) • Ze względu na ważne zastosowania istnieje teoria, która pozwala na identyfikacją takich zależności. Trzeba w tym celu spełnić pewne dodatkowe wymagania (równe odstępy pomiędzy wartościami zmiennej niezależnej, etc. ) • Istotne problemy do przeanalizowania: – jednoznaczność rozwiązania – Obiektywna ocena jakości aproksymacji

Aproksymacja Rank conditions • A – macierz, rank A – rząd macierzy A. • Rząd macierzy jest równy liczbie jej liniowo niezależnych kolumn. • Twierdzenie 1: liczba liniowo niezależnych wierszy i liniowo niezależnych kolumn są takie same. • Wniosek 1: rank Anxm min(n, m). • Wniosek 2: rank A = rank AT. • Twierdzenie 2: rank AB = min(rank A, rank B) • Układ równań Grama ma zawsze rozwiązanie • Układ równań Grama ma jednoznaczne rozwiązanie jeżeli |G| 0 • |G| 0 rank G = n. • rank G = rank XTX = min(rank X, rank XT) = rank X. • Wniosek: rank X = n. • rank Xkxn min(n, k). • Wniosek: X musi być macierzą o maksymalnym rzędzie (tzn. n). • Konieczny warunek jednoznaczności identyfikacji: n k. • Własnymi słowami: liczba istotnych pomiarów nie może być za mała.

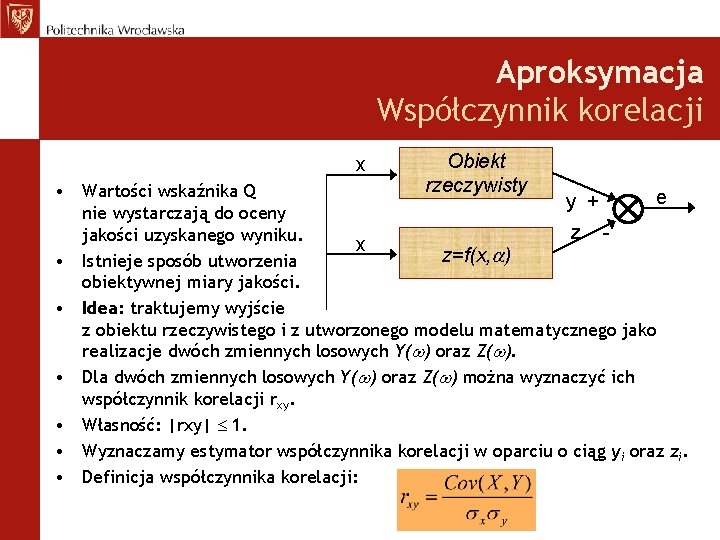
Aproksymacja Współczynnik korelacji x Obiekt rzeczywisty • Wartości wskaźnika Q e y + nie wystarczają do oceny z jakości uzyskanego wyniku. x z=f(x, ) • Istnieje sposób utworzenia obiektywnej miary jakości. • Idea: traktujemy wyjście z obiektu rzeczywistego i z utworzonego modelu matematycznego jako realizacje dwóch zmiennych losowych Y( ) oraz Z( ). • Dla dwóch zmiennych losowych Y( ) oraz Z( ) można wyznaczyć ich współczynnik korelacji rxy. • Własność: |rxy| 1. • Wyznaczamy estymator współczynnika korelacji w oparciu o ciąg yi oraz zi. • Definicja współczynnika korelacji: