Metody Matematyczne w Inynierii Chemicznej Podstawy oblicze statystycznych

Metody Matematyczne w Inżynierii Chemicznej Podstawy obliczeń statystycznych

STSTYSTYKA - definicje • Zastosowanie matematycznego rachunku prawdopodobieństwa do próbek tak, by – wnioski dotyczące populacji wysnute na ich podstawie można było umieścić w określonych granicach. – określić czy jakiś parametr wpływa na uzyskane wyniki • Gromadzenie danych przez urzędy i instytucje (np. GUS)

Rozkłady zmiennej losowej

Zmienna losowa • Zmienna, której wartość nie jest jednoznacznie określona (jej wartość może się zmieniać). Różne wartości zmiennej losowej mają zwykle różne prawdopodobieństwo pojawienia się. • Zmienne losowe mogą być: – dyskretne (skokowe) o skończonym/policzalnym zbiorze wartości – ciągłe – zbiór wartości jest nieskończony (przedział liczb rzeczywistych)

Rozkład zmiennej losowej • Jest to funkcja związana z prawdopodobieństwem pojawienia się pewnych wartości danej zmiennej losowej (opis wartości przyjmowanych przez zmienną losową przy pomocy prawdopodobieństw z jakim są one przyjmowane)

Rozkład zmiennej losowej • Rozróżnia się dwa typy takich funkcji: – dystrybuanta – określa prawdopodobieństwo wystąpienia wartości zmiennej losowej x mniejszej lub równej pewnej wartości x F(x) = P(x<x) Funkcja ta jest zawsze niemalejąca. – gęstość prawdopodobieństwa – jest to pochodna dystrybuanty – określa prawdopodobieństwo przyjęcia przez zmienna losową x wartości równej x

Najpopularniejsze rozkłady zmiennej losowej • • Rozkład jednostajny Rozkład dwumianowy (Bernouliego) Rozkład Poissona Rozkład normalny (Gaussa)

Rozkład jednostajny • Zmienna może przyjąć dowolną wartość z przedziału od a do b z takim samym prawdopodobieństwem ciągły dyskretny

Rozkład dwumianowy (Bernoulliego) • to dyskretny rozkład prawdopodobieństwa opisujący ilość sukcesów r w ciągu n niezależnych prób, z których każda ma stałe prawdopodobieństwo sukcesu równe p.

Rozkład dwumianowy (Bernoulliego) • Zastosowanie: – Obliczenie prawdopodobieństwa zajścia jakiegoś zdarzenia w próbce przy znanym prawdopodobieństwie w populacji i liczebności próbki – Obliczenie przedziału, w którym mieści się rzeczywista liczebność w populacji przy znanej liczebności w próbce i założonym prawdopodobieństwie

Rozkład dwumianowy, obliczenie w Excelu Funkcja statystyczna: ROZKŁAD. DWUM r n p

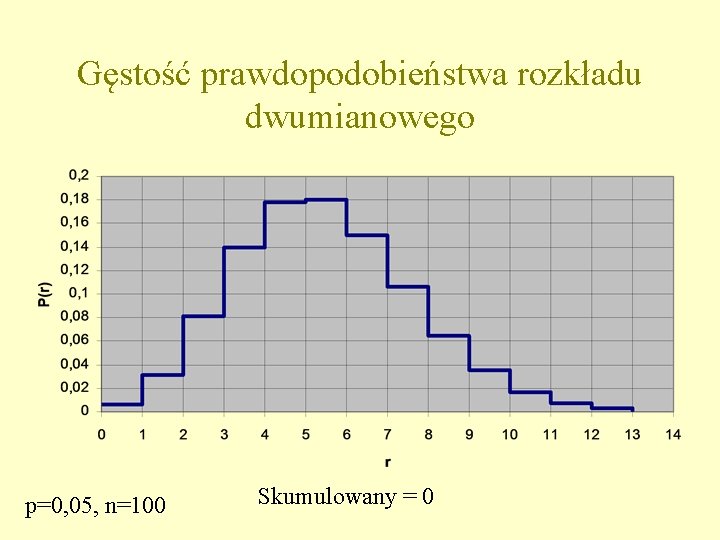
Gęstość prawdopodobieństwa rozkładu dwumianowego p=0, 05, n=100 Skumulowany = 0

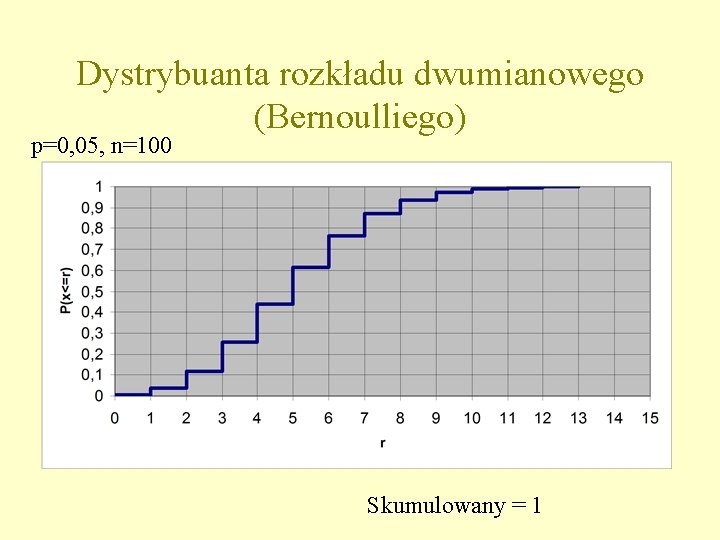
Dystrybuanta rozkładu dwumianowego (Bernoulliego) p=0, 05, n=100 Skumulowany = 1

Rozkład dwumianowy • W praktyce najczęściej dysponujemy próbką i na tej podstawie wyciągamy wnioski dotyczące populacji. • Znając częstość w próbce, częstość w populacji może być taka sama a prawdopodobieństwo jej wystąpienia będzie wynosić tyle ile max. na wykresie gęstości prawdopodobieństwa • Prawdopodobieństwo pochodzenia próbki z populacji o innej częstości będzie mniejsze ale nie zerowe

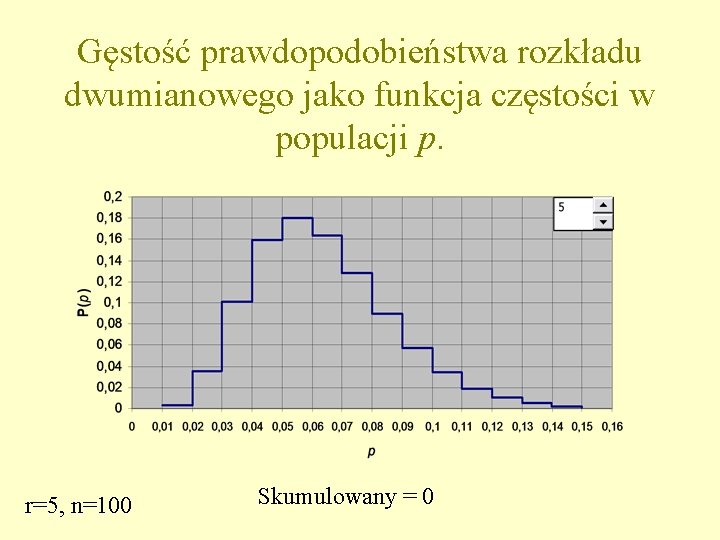
Gęstość prawdopodobieństwa rozkładu dwumianowego jako funkcja częstości w populacji p. r=5, n=100 Skumulowany = 0

Rozkład dwumianowy • Można sporządzić wykres dystrybuanty (prawdopodobieństwa skumulowanego) jako funkcji częstości w populacji dla danej ilości sukcesów w próbce.

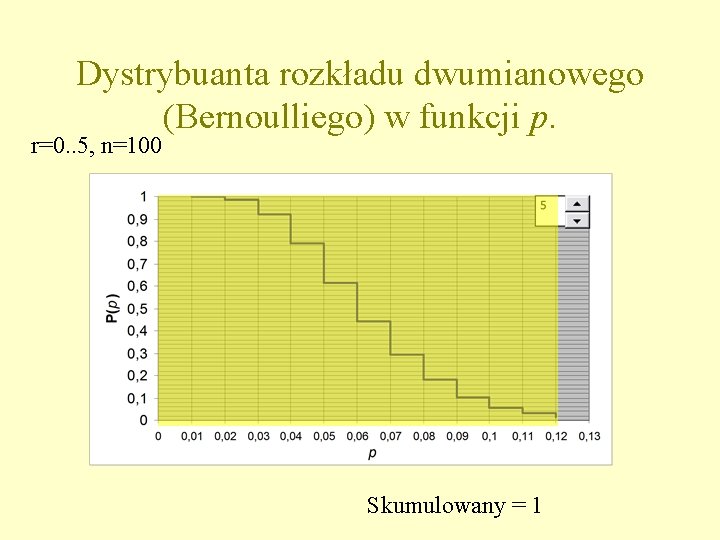
Dystrybuanta rozkładu dwumianowego (Bernoulliego) w funkcji p. r=0. . 5, n=100 Skumulowany = 1

• Z takiego wykresu można wywnioskować z prawdopodobieństwem ok. 97. 5%, że 5 zdarzeń na 100 w próbce może zajść jeżeli w populacji częstość p wynosi do 11% – z prawdopodobieństwem popełnienia błędu ok. 2, 5% można stwierdzić, że jeżeli w próbce jest 5 zdarzeń na 100 to w populacji częstość wynosi do 11%

• Wystąpienie od 0 do 5 zdarzeń w próbce jest niejednoznaczne. Interesujące jest wystąpienie dokładnie 5 zdarzeń • W tym celu wykorzystuje się dodatkowo dystrybuantę zajścia od 5 do 100 w próbce. • połączenie tych dwóch dystrybuant (ich część wspólna to r=5) pozwala znaleźć związek między próbką a populacją.

• Dystrybuantę można wyznaczyć obliczając prawdopodobieństwo wystąpienia od 0 do 4 zdarzeń i odejmując je od 1

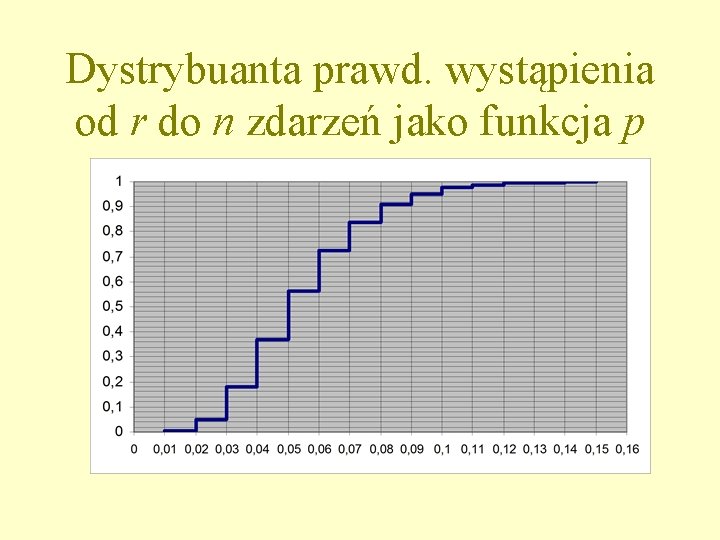
Dystrybuanta prawd. wystąpienia od r do n zdarzeń jako funkcja p

• Z wykresu można odczytać, że prawdopodobieństwo takie przekracza wartość 2, 5% dla częstości w populacji na poziomie 2% • Łącząc te dwie dystrybuanty otrzymamy symetryczny przedział ufności, odrzucający rozkłady w populacji mogące wystąpić rzadziej niż 2, 5%+2, 5%=5%

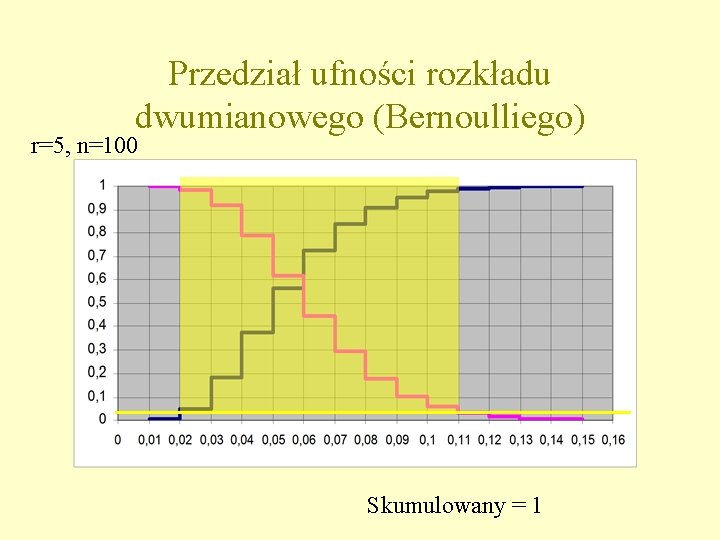
Przedział ufności rozkładu dwumianowego (Bernoulliego) r=5, n=100 Skumulowany = 1

Przedział ufności rozkładu dwumianowego • Sposób obliczania granic przedziału w Excelu: – Górna granica przedziału ufności: • Obliczamy P skumulowane dla danego r i n oraz wstępnie założonej częstości w populacji p • znajdujemy takie p (funkcja szukaj wyniku), przy którym P osiąga wartość (1 -PU)/2, gdzie PU to pożądany poziom ufności – Dolna granica przedziału ufności • Obliczamy 1 -P skumulowane dla danego r-1 (dla r=0 przyjąć r-1=0) i n oraz wstępnie założonej częstości w populacji p • znajdujemy takie p (funkcja szukaj wyniku), przy którym P osiąga wartość (1 -PU)/2, gdzie PU to pożądany poziom ufności

Rozkład Poissona Definicja: Granicą do jakiej dąży rozkład dwumianowy, gdy częstość w populacji p maleje oraz rozmiar próbki rośnie jest rozkład Poissona. Prawdopodobieństwo, że zdarzenie zajdzie w próbce dokładnie r razy oblicza się z następującego równania: Gdzie: m = n·p, czyli jest to średnia wartość oczekiwanych zdarzeń w próbce.

Rozkład Poissona r n*p

Rozkład normalny - Gaussa • DEFINICJA równanie krzywej normalnej jako gęstości prawdopodobieństwa y lub częstości względnej, wyrażonej jako funkcja zmiennej losowej x ma postać: gdzie: m – średnia wartość zmiennej x s – odchylenie standardowe

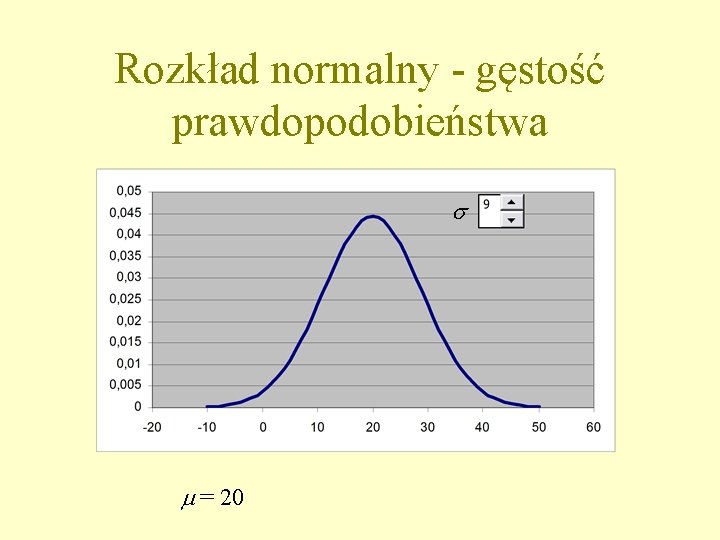
Rozkład normalny - gęstość prawdopodobieństwa s m = 20

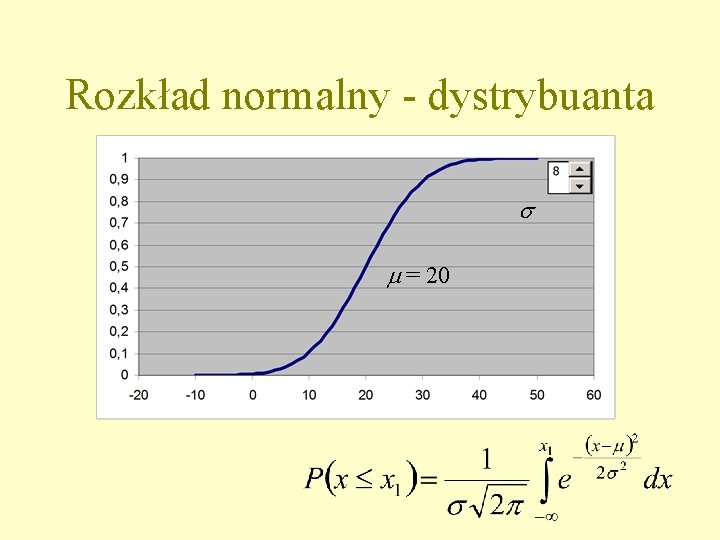
Rozkład normalny - dystrybuanta s m = 20

Rozkład normalny - Gaussa

Rozkład normalny - Gaussa

• Zmienna standaryzowana: każdą wartość zmiennej losowej x można wyrazić w ilościach jednostek z odchylenia standardowego – zmienna taka jest uniwersalna, niezależna od zmiennej losowej. Wartość średnia wynosi 0

Rozkład Gaussa • Poziom istotności • Poziom ufności

Miary zmienności

Miary tendencji centralnej • Wartość średnia (średnia arytmetyczna) • Wartość modalna – Wartość występująca najczęściej • Mediana – Wartość, przy której dystrybuanta osiąga 0, 5 • Średnia geometryczna

Miary zmienności • Odchylenie standardowe – Oszacowanie odchylenia standardowego na podstawie próbki

Miary zmienności • Wariancja

Excel Testy statystyczne

Test 2 • Dotyczy zmiennych zliczeniowych (enumeracyjnych) • Wprowadził go Karol Pearson w 1899 r. • Opiera się na stosunku rzeczywistej i oczekiwanej częstości wystąpienia jakiegoś zdarzenia losowego. Z – zaobserwowana częstość występowania danego zdarzenia O – oczekiwana częstość występowania danego zdarzenia

Test 2 • Wartość 2 jest miara odchyleń rzeczywistych zdarzeń od oczekiwań

Test - hipoteza zerowa 2 • Do zastosowania rozkładu 2 potrzebna jest podstawa do określenia wartości oczekiwanych: – Wyniki poprzednich doświadczeń – Wartość przyjęta a‘priori • Niezależnie od określenia wartości oczekiwanej stawia się hipotezę, że wyniki zaobserwowane z próbki są takie jak oczekiwane

Test 2 • Wartości 2 jakich można oczekiwać przy danej liczbie stopni swobody (ilości niezależnych pomiarów) z określonym prawdopodobieństwem zestawione są w tabelach LUB • Można je wyliczyć za pomocą np. Excela

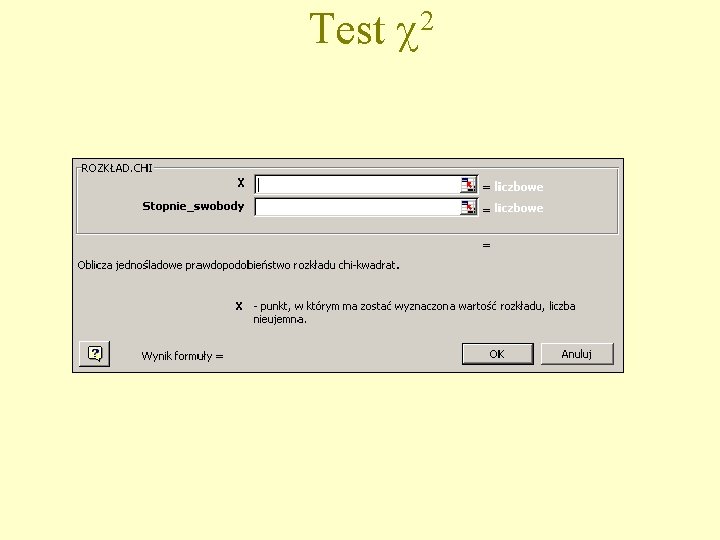
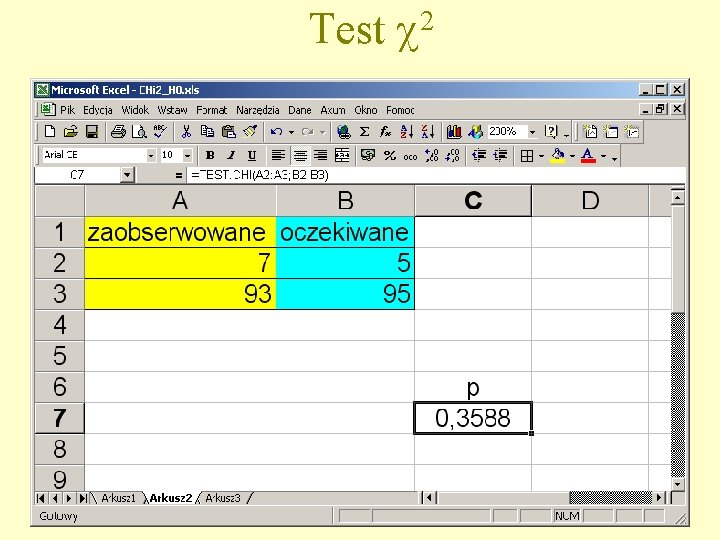
Test 2

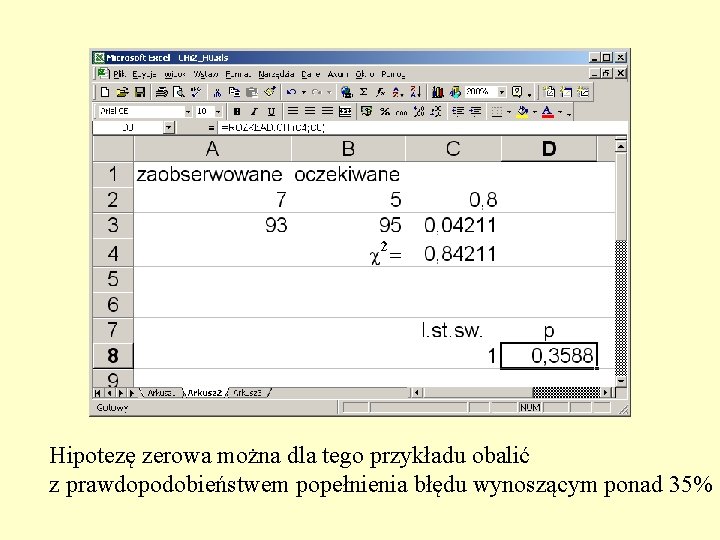
Hipotezę zerowa można dla tego przykładu obalić z prawdopodobieństwem popełnienia błędu wynoszącym ponad 35%

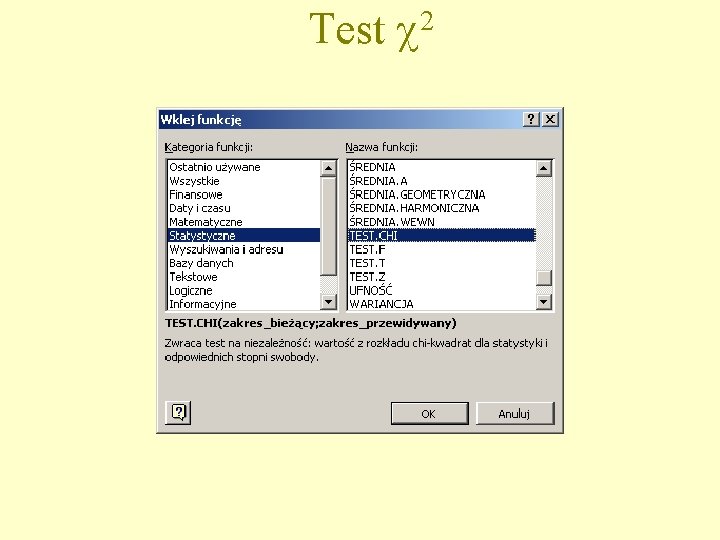
Test 2

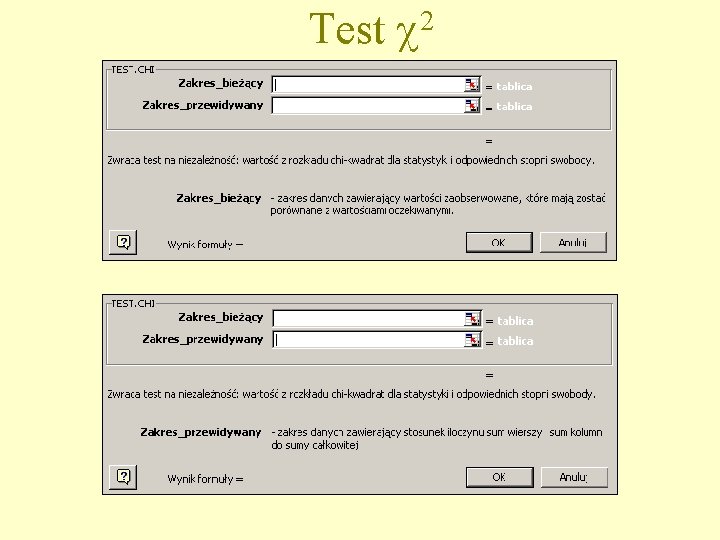
Test 2

Test 2

Test t • Dotyczy oszacowania prawdziwej średniej m w populacji na podstawie średniej x próbki oraz ustalenia przedziału ufności, w granicach którego mieści się prawdziwa wartość • Wartość t definiuje wzór analogiczny do zmiennej standaryzowanej: Oszacowany błąd standardowy

Oszacowany błąd standardowy Oszacowane odchylenie standardowe populacji s(x)

Test t • Zmienną t na określonym poziomie ufności można odczytać z tabel lub obliczyć za pomocą programów z funkcjami statystycznymi • Wartość t zależy od ilości stopni swobody • Jeżeli obliczona t jest większa od odczytanej to z prawdopodobieństwem popełnienia błędu p hipotezę zerową można odrzucić

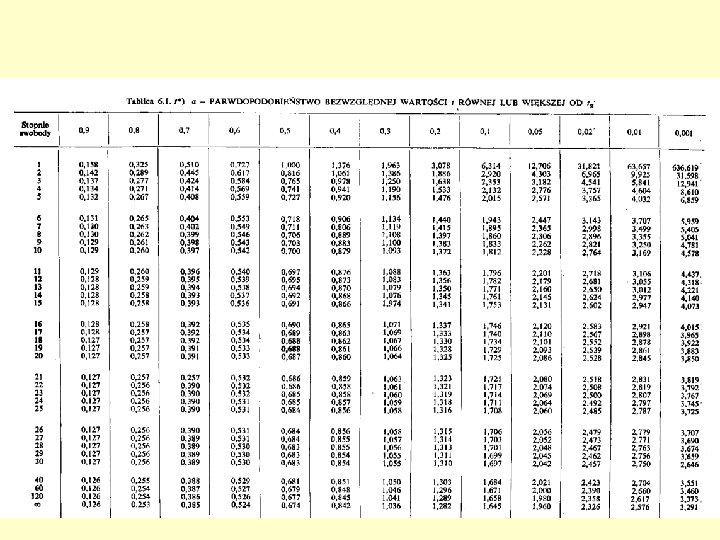
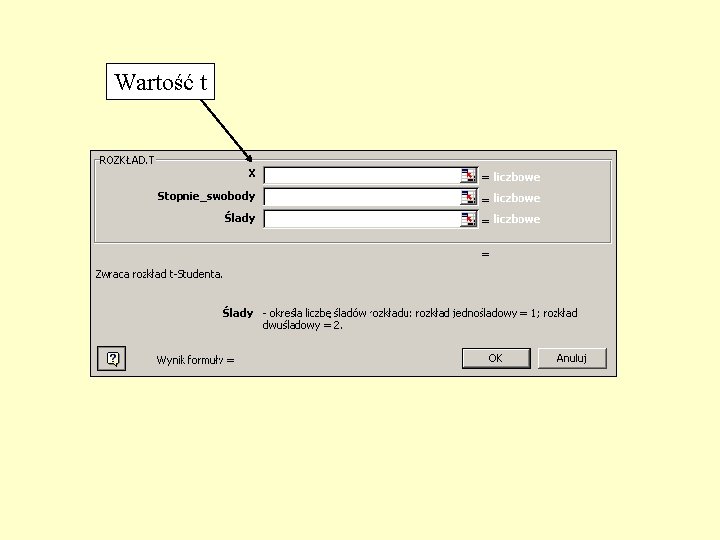
Wartość t

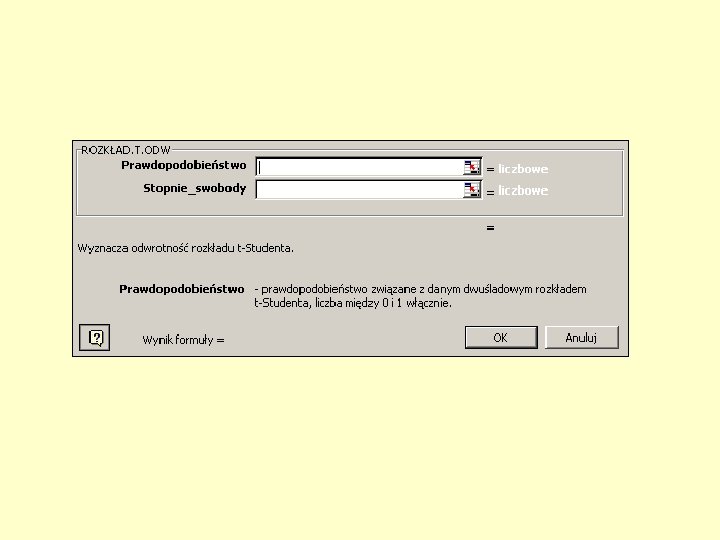
Oszacowany błąd standardowy Oblicza oszacowane odchylenie std. w populacji Oblicza ilość danych n

Wykorzystanie testu t, przykład.

Test t dostępny w Excelu służy do porównania dwóch próbek 1 Sparowany 2 Wariancja równa dla dwóch prób 3 Wariancja nierówna dla dwóch prób

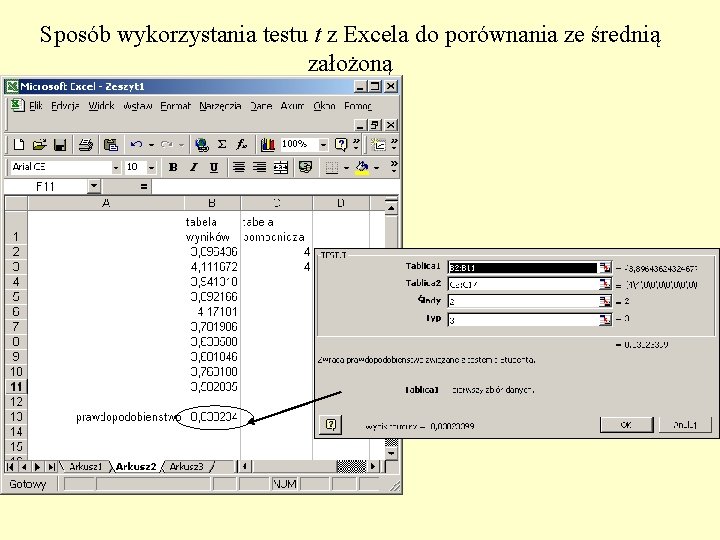
Sposób wykorzystania testu t z Excela do porównania ze średnią założoną

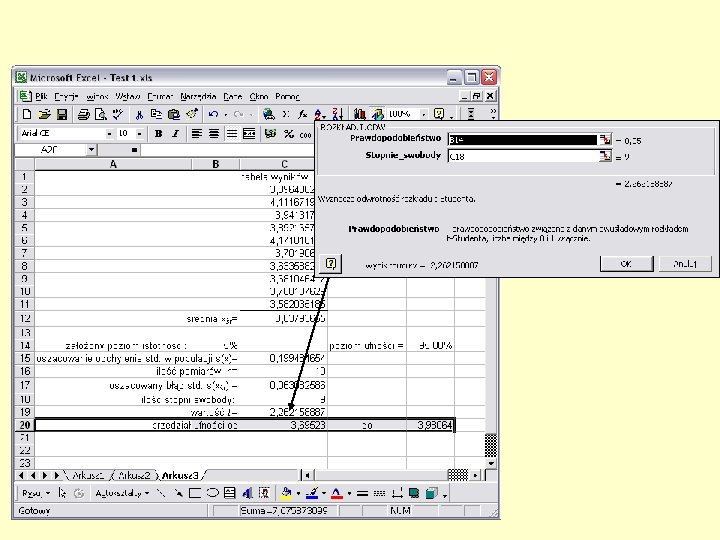
Test t • Oszacowanie prawdziwej średniej – przedział ufności – Funkcja t przedstawia rozkład odchyleń xśr od m w funkcji prawdopodobieństwa wystąpienia tych odchyleń – Z przekształconego równania definicyjnego • Z podanym w tablicach prawdopodobieństwem popełnienia błędu prawdziwa średnia mieści się w tym przedziale • przedział ufności nazywa się zazwyczaj jako (1 -p)100% np. poziom istotności 0, 05 to poziom ufności jest 95%