METODO DE CROUT INTEGRANTES SERRANO SANDOVAL CARLOS LUCCA

METODO DE CROUT INTEGRANTES SERRANO SANDOVAL CARLOS LUCCA VELEZ ZAPANA LUIS FERNANDO OVIEDO ACOSTA NATALIA ALVAREZ ORIAS GENARO MAURICIO TAPIA HURTADO VALERIA VERA MONTOYA BRAYAN LARUTA CORONEL ANDREA GERALDINNE

INTRODUCCION En la siguiente exposición vamos a conceptualizar, explicar y realizar ejercicios del método de Factorización o Descomposición de Crout. Este método es denominado formalmente Método de Doolittle y sirve como una alternativa al Método de Descomposición LU. Además hay un derivado del método de Crout llamado Método de Gauss-Crout.

OBJETIVOS Estudiar el método de Factorización o Descomposición de Crout con la finalidad de facilitar la solución de sistemas de ecuaciones. Realizar un software que realice este método.

BIOGRAFIA Prescott Duran Crout nació el 28 de julio de 1907, fue un matemático americano nacido de Ohio. Vivió y trabajó en Massachusetts. En 1929 se graduó de MIT. Su tesis de doctorado fue titulado “La aproximación de funciones e Integrales mediante una combinación lineal de función”. Crout fue miembro de la Facultad de Matemáticas desde 1934 hasta 1973. El formaba parte del personal de laboratorio de Radiación desde 1934 hasta 1945. Crout es el autor del libro “La determinación de campos satisfaciendo Laplace, Poisson y ecuaciones asociadas”.

FACTORIZACION CROUT En el método de Crout la matriz A es factorizada como A= LU en donde la matriz L es una matriz triangular inferior y U una matriz triangular superior con diagonal unitaria. El método de Crout es un procedimiento del tipo recursivo, esto significa el desarrollo de un conjunto de pasos sucesivos en donde el trabajo a realizar en cada paso resulta similar o del mismo tipo pero basado en resultados obtenidos en pasos anteriores. Estos pasos consisten en la descomposición sucesiva de los menores principales de la matriz de coeficientes A. De manera similar al método de Choleski se hace la siguiente consideración para poder obtener los coeficientes de L y U.

GENERALIDADES Para este método de factorización directa de matrices, se utiliza como fundamento que los valores de la diagonal de la matriz U, son todos uno (1). El procedimiento a seguir para la aplicación del método es el siguiente: Se debe construir una matriz de coeficientes y el vector con los términos independientes, correspondientes al sistema, y se toman como valores iniciales para poder calcular la factorización. Tomando la matriz de coeficientes, y bajo el fundamento principal del método, se procese al cálculo de las matrices L y U, correspondientes a la factorización de A.

Una vez realizada la factorización, se toma la matriz L y los términos independientes y se procede a calcular el vector D. Con el vector D y la matriz U de la factorización, calculamos el vector X. El método de Descomposición de Crout genera [U] y [L] barriendo las columnas y renglones de la matriz.

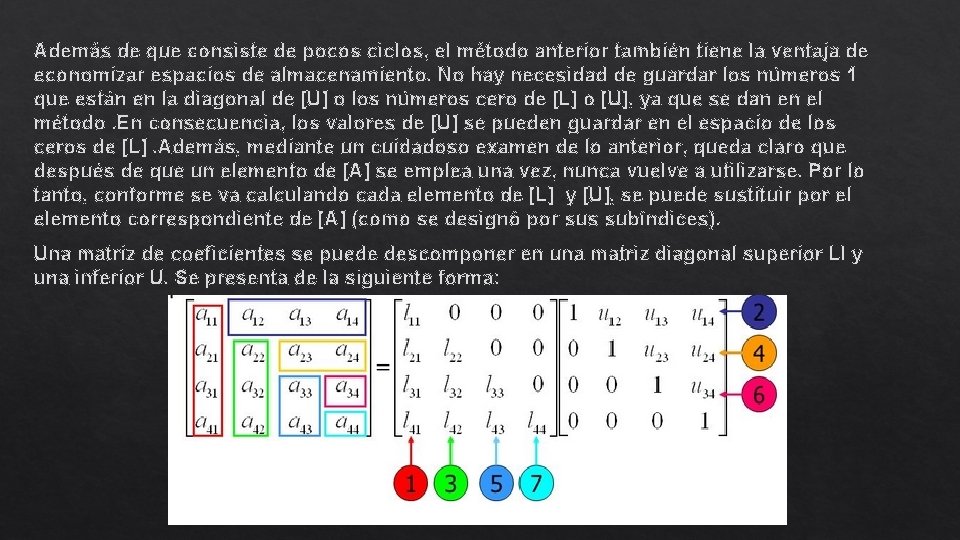
Además de que consiste de pocos ciclos, el método anterior también tiene la ventaja de economizar espacios de almacenamiento. No hay necesidad de guardar los números 1 que están en la diagonal de [U] o los números cero de [L] o [U], ya que se dan en el método. En consecuencia, los valores de [U] se pueden guardar en el espacio de los ceros de [L]. Además, mediante un cuidadoso examen de lo anterior, queda claro que después de que un elemento de [A] se emplea una vez, nunca vuelve a utilizarse. Por lo tanto, conforme se va calculando cada elemento de [L] y [U], se puede sustituir por el elemento correspondiente de [A] (como se designó por sus subíndices). Una matriz de coeficientes se puede descomponer en una matriz diagonal superior Ll y una inferior U. Se presenta de la siguiente forma:

PASOS PARA RESOLVER EL MÉTODO DE CROUT 1. -Construir las matrices L y U si es posible a partir de A = LU [A][x] =[b] [A] = [L] [U] 2. -Resolver LD=B con sustitución normal 3. -Resolver UX=D

CONCLUSIONES ESTE UN METODO DE FORMULACION MODERNA , QUE NOS AYUDA A SIMPLIFICAR DIVERSOS SISTEMAS DE ECUACIONES LINEALES. ESTE METODO SIMPLIFICA EL GRADO DE DIFICULTAD EN EL DESARROLLO A MANO DE SISTEMAS ECUACIONES. PRESCOTT CROUT, PROFESOR DE MATEMÁTICAS EN EL MIT (MASSACHUSETTS INSTITUTE OF TECHNOLOGY) APLICÓ EL MÉTODO DE ELIMINACIÓN A PROBLEMAS DE INGENIERÍA ELÉCTRICA EN 1941. SU ALGORITMO FUE EL ÚLTIMO PUBLICADO PENSADO SÓLO PARA HACER CÁLCULOS A MANO.