METODE TRANSPORTASI PENGERTIAN metode yang digunakan untuk mengatur

METODE TRANSPORTASI

PENGERTIAN • metode yang digunakan untuk mengatur distribusi dari sumber- sumber yang menyediakan produk yang sama ke tempat-tempat yang membutuhkan secara optimal. Alokasi produk ini harus diatur sedemikian rupa, karena terdapat perbedaan biaya-biaya alokasi dari satu sumber ke suatu tempat tujuan

METODE-METODE • North West Corner (NWC) • Least Cost (LC) • Vogels Approximation

NORTH WEST CORNER • Metode ini adalah metode yang paling sederhana diantara metode untuk mencari solusi awal, karena tidak mempertimbangkan biaya transportasi (Siagian; 1987; 159). Algoritma metode pojok kiri atas pojok kanan bawah (North West Corner Method) untuk mencapai solusi fisibel awal dari masalah transportasi adalah sebagai berikut :

NORTH WEST CORNER • 1. Memulai dari pojok barat laut alokasikan sebesar X 11 = min(a 1, b 1). o Bila a 1 > b 1, maka X 11 = b 1. Teruskan ke sel (1, 2) yaitu gerakan mendatar dimana X 12 = min(a 1 -b 1, b 2). o Bila a 1 < b 1, maka X 11 = a 1. Teruskan ke sel (2, 1) yaitu gerakan tegak dimana X 21 = min (b 1 -a 1, a 2). o Bila a 1 = b 1, maka buatlah X 11 = a 1 = b 1 dan gerakan teruskan ke X 12 (gerakan miring). • 2. Meneruskan langkah ini, sehingga mendekati pojok barat laut hingga akhirnya sampai semua penawaran telah dihabiskan dan keperluan permintaan telah terpenuhi.

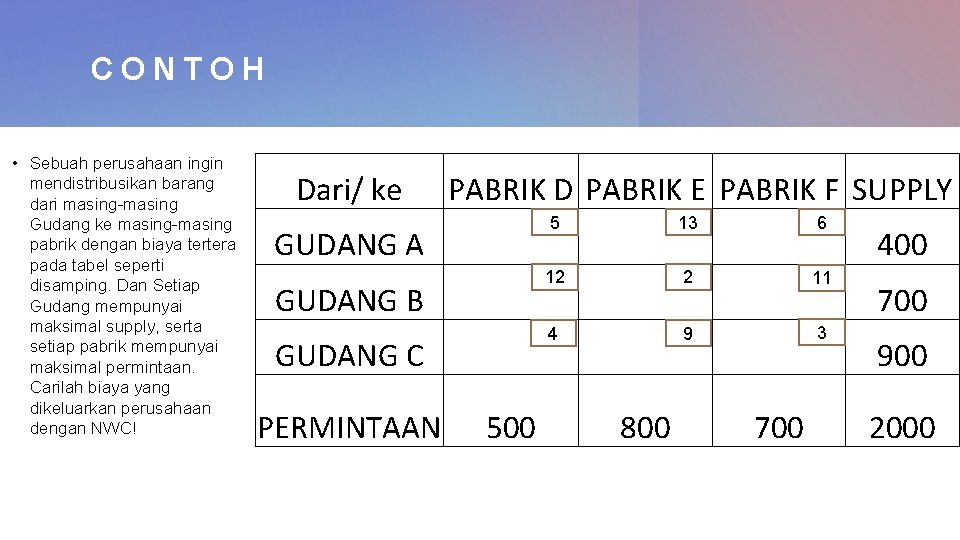
CONTOH • Sebuah perusahaan ingin mendistribusikan barang dari masing-masing Gudang ke masing-masing pabrik dengan biaya tertera pada tabel seperti disamping. Dan Setiap Gudang mempunyai maksimal supply, serta setiap pabrik mempunyai maksimal permintaan. Carilah biaya yang dikeluarkan perusahaan dengan NWC! Dari/ ke GUDANG A GUDANG B PABRIK D PABRIK E PABRIK F SUPPLY GUDANG C PERMINTAAN 500 5 12 4 800 13 2 9 700 6 11 3 400 700 900 2000

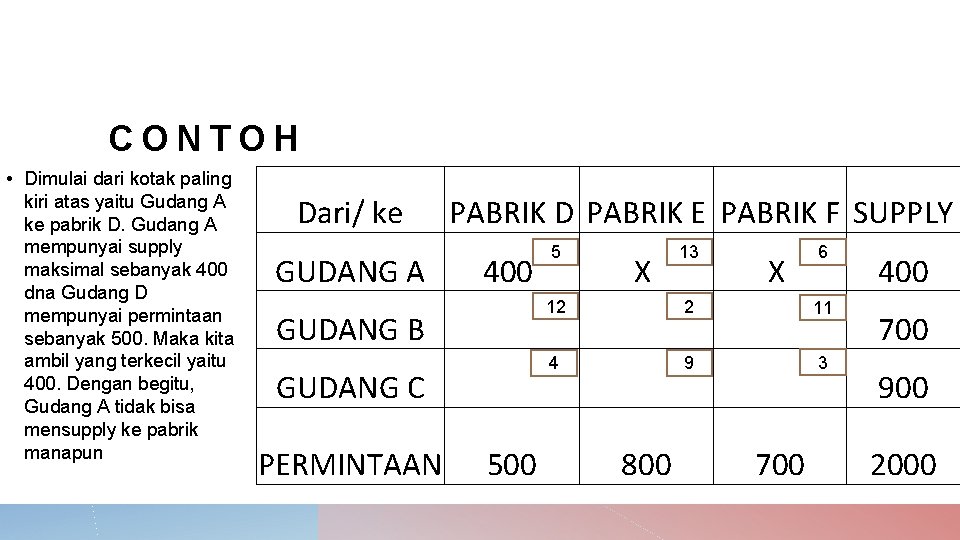
CONTOH • Dimulai dari kotak paling kiri atas yaitu Gudang A ke pabrik D. Gudang A mempunyai supply maksimal sebanyak 400 dna Gudang D mempunyai permintaan sebanyak 500. Maka kita ambil yang terkecil yaitu 400. Dengan begitu, Gudang A tidak bisa mensupply ke pabrik manapun Dari/ ke GUDANG A GUDANG B PABRIK D PABRIK E PABRIK F SUPPLY 400 GUDANG C PERMINTAAN 500 5 12 4 X 800 13 2 9 X 700 6 11 3 400 700 900 2000

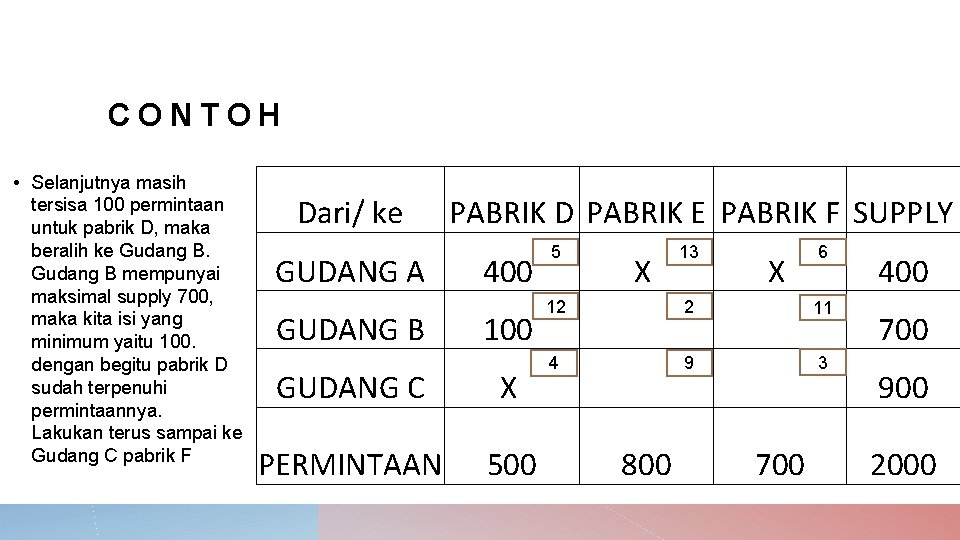
CONTOH • Selanjutnya masih tersisa 100 permintaan untuk pabrik D, maka beralih ke Gudang B mempunyai maksimal supply 700, maka kita isi yang minimum yaitu 100. dengan begitu pabrik D sudah terpenuhi permintaannya. Lakukan terus sampai ke Gudang C pabrik F Dari/ ke GUDANG A GUDANG B PABRIK D PABRIK E PABRIK F SUPPLY 400 100 GUDANG C X PERMINTAAN 500 5 12 4 X 800 13 2 9 X 700 6 11 3 400 700 900 2000

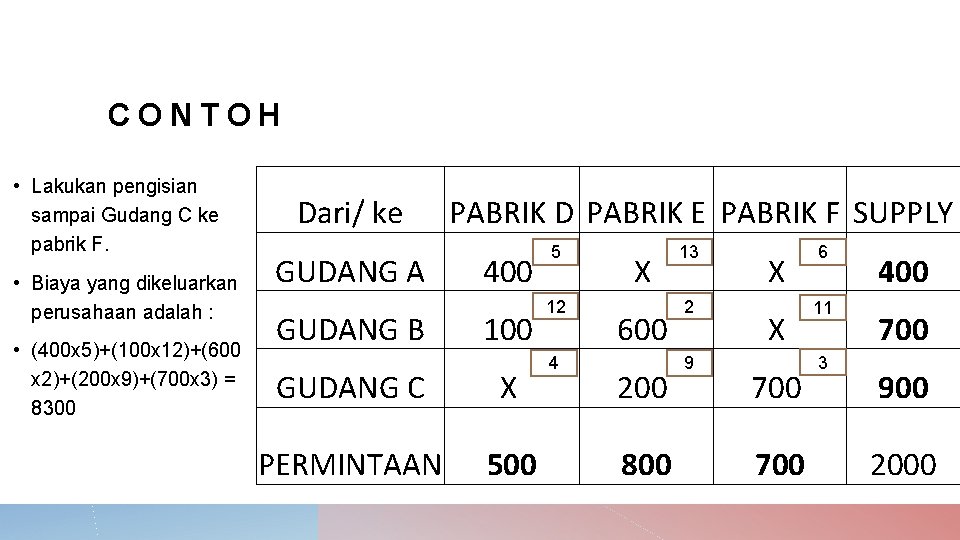
CONTOH • Lakukan pengisian sampai Gudang C ke pabrik F. • Biaya yang dikeluarkan perusahaan adalah : • (400 x 5)+(100 x 12)+(600 x 2)+(200 x 9)+(700 x 3) = 8300 Dari/ ke GUDANG A GUDANG B PABRIK D PABRIK E PABRIK F SUPPLY 400 100 GUDANG C X PERMINTAAN 500 5 12 4 X 600 200 800 13 2 9 X X 700 6 11 3 400 700 900 2000

LEAST COST • Algoritma metode ongkos terkecil (Least Cost Method) untuk mencapai solusi fisibel awal dari masalah transportasi adalah sebagai berikut : 1. Menyusun tabel awal yang berisi tabel biaya transportasi. 2. Mencari sel yang memiliki biaya terkecil Cij pada tabel awal.

LEAST COST 3. Pada Cij terkecil dialokasikan sebanyak mungkin tanpa melanggar batasannya. Mengisi Xij = min(ai, bj). o Jika bj < ai maka Xij = bj kolom ke j tidak diperhitungkan lagi dan ai berkurang sebesar bj. o Jika bj > ai maka Xij = ai baris ke i tidak diperhitungkan lagi dan bj berkurang sebesar ai. o Jika bj = ai maka Xij= ai = bj baris ke i dan kolom ke j tidak diperhitungkan lagi. 4. Mencari sel yang memiliki Cij terkecil, dilanjutkan dengan cara yang sama sampai semua persediaan habis dan permintaan terpenuhi.

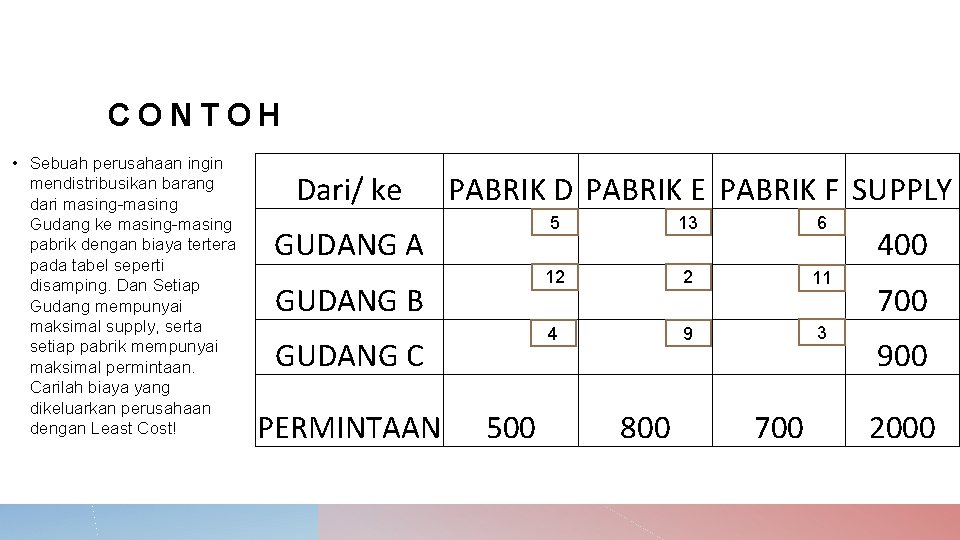
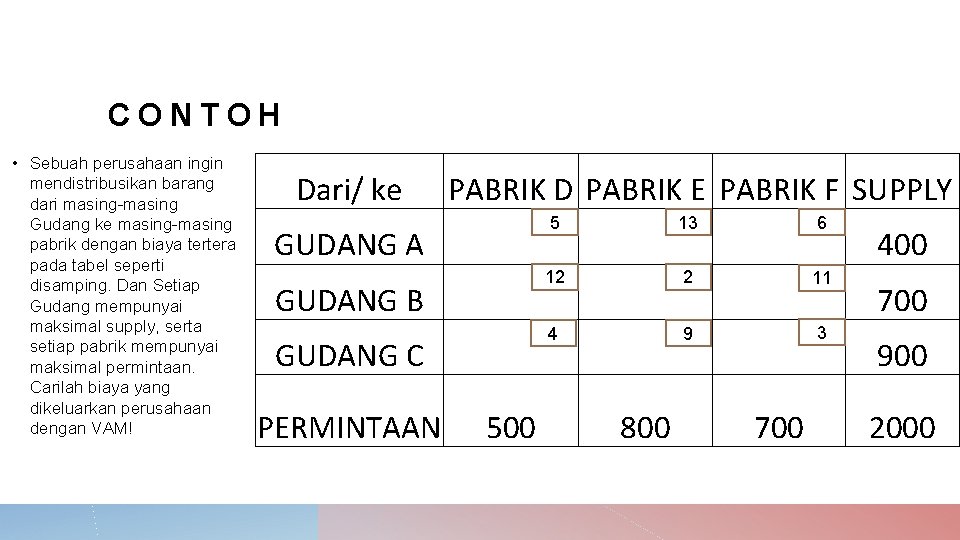
CONTOH • Sebuah perusahaan ingin mendistribusikan barang dari masing-masing Gudang ke masing-masing pabrik dengan biaya tertera pada tabel seperti disamping. Dan Setiap Gudang mempunyai maksimal supply, serta setiap pabrik mempunyai maksimal permintaan. Carilah biaya yang dikeluarkan perusahaan dengan Least Cost! Dari/ ke GUDANG A GUDANG B PABRIK D PABRIK E PABRIK F SUPPLY GUDANG C PERMINTAAN 500 5 12 4 800 13 2 9 700 6 11 3 400 700 900 2000

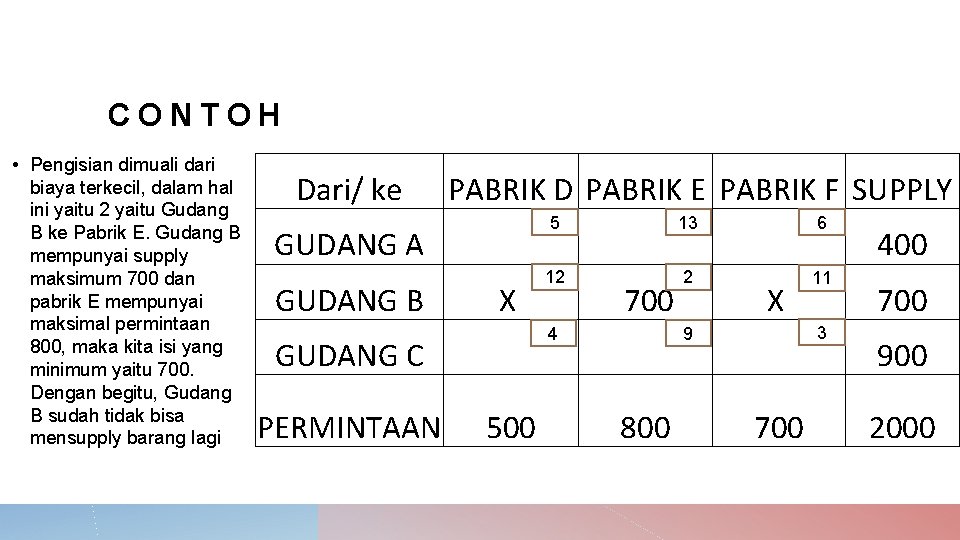
CONTOH • Pengisian dimuali dari biaya terkecil, dalam hal ini yaitu 2 yaitu Gudang B ke Pabrik E. Gudang B mempunyai supply maksimum 700 dan pabrik E mempunyai maksimal permintaan 800, maka kita isi yang minimum yaitu 700. Dengan begitu, Gudang B sudah tidak bisa mensupply barang lagi Dari/ ke GUDANG A GUDANG B PABRIK D PABRIK E PABRIK F SUPPLY X GUDANG C PERMINTAAN 500 5 12 4 700 800 13 2 9 X 700 6 11 3 400 700 900 2000

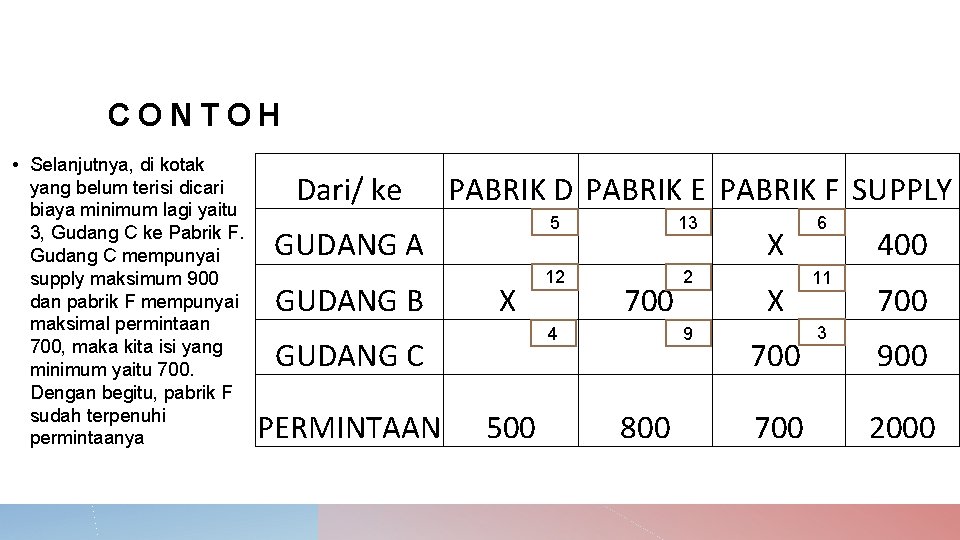
CONTOH • Selanjutnya, di kotak yang belum terisi dicari biaya minimum lagi yaitu 3, Gudang C ke Pabrik F. Gudang C mempunyai supply maksimum 900 dan pabrik F mempunyai maksimal permintaan 700, maka kita isi yang minimum yaitu 700. Dengan begitu, pabrik F sudah terpenuhi permintaanya Dari/ ke GUDANG A GUDANG B PABRIK D PABRIK E PABRIK F SUPPLY X GUDANG C PERMINTAAN 500 5 12 4 700 800 13 2 9 X X 700 6 11 3 400 700 900 2000

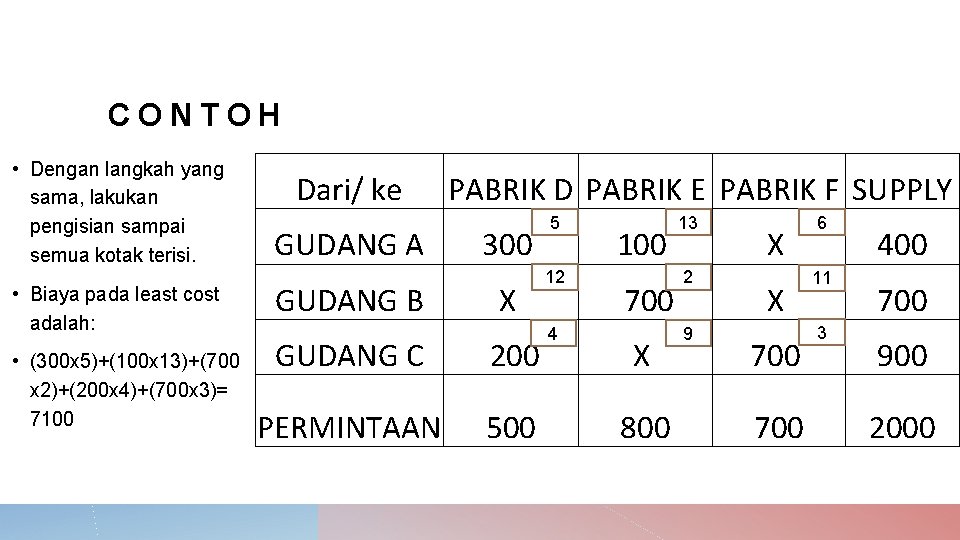
CONTOH • Dengan langkah yang sama, lakukan pengisian sampai semua kotak terisi. • Biaya pada least cost adalah: • (300 x 5)+(100 x 13)+(700 x 2)+(200 x 4)+(700 x 3)= 7100 Dari/ ke GUDANG A GUDANG B PABRIK D PABRIK E PABRIK F SUPPLY 300 X GUDANG C 200 PERMINTAAN 500 5 12 4 100 700 X 800 13 2 9 X X 700 6 11 3 400 700 900 2000

VOGEL’S APPROXIMATION • Algoritma metode VAM (Vogel’s Approximation Method) untuk mencapai solusi fisibel awal dari masalah transportasi adalah sebagai berikut : 1. Menyusun kebutuhan, kapasitas masing-masing sumber dan biaya pengangkutan kedalam matriks. 2. Mencari selisih biaya terkecil dengan biaya terkecil berikutnya untuk setiap kolom maupun baris. 3. Memilih selisih biaya terbesar dan mengalokasikan produk sebanyak mungkin ke sel yang memiliki biaya terkecil.

VOGEL’S APPROXIMATION 4. Menghilangkan baris atau kolom yang sudah diisi sepenuhnya karena tidak mungkin diisi lagi. 5. Menentukan kembali perbedaan (selisih) biaya pada langkah 2 untuk kolom dan baris yang belum terisi. Ulangi langkah 3 sampai dengan langkah 5, sampai semua kolom dan baris teralokasi. 6. Setelah terisi semua, kemudian menghitung biaya transportasi secara keseluruhan. 7. Melakukan Uji Optimalitas

CONTOH • Sebuah perusahaan ingin mendistribusikan barang dari masing-masing Gudang ke masing-masing pabrik dengan biaya tertera pada tabel seperti disamping. Dan Setiap Gudang mempunyai maksimal supply, serta setiap pabrik mempunyai maksimal permintaan. Carilah biaya yang dikeluarkan perusahaan dengan VAM! Dari/ ke GUDANG A GUDANG B PABRIK D PABRIK E PABRIK F SUPPLY GUDANG C PERMINTAAN 500 5 12 4 800 13 2 9 700 6 11 3 400 700 900 2000

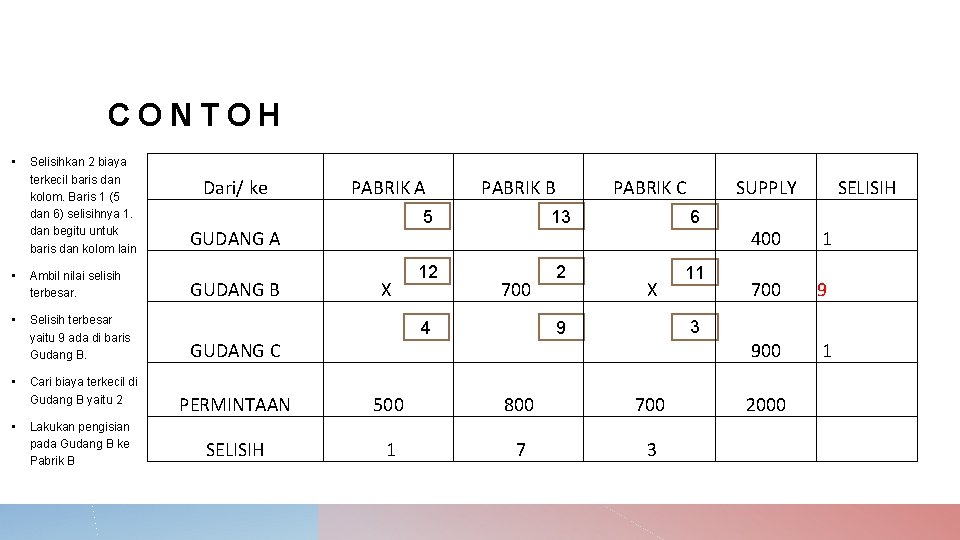
CONTOH • Selisihkan 2 biaya terkecil baris dan kolom. Baris 1 (5 dan 6) selisihnya 1. dan begitu untuk baris dan kolom lain • Ambil nilai selisih terbesar. • Selisih terbesar yaitu 9 ada di baris Gudang B. • • Cari biaya terkecil di Gudang B yaitu 2 Lakukan pengisian pada Gudang B ke Pabrik B Dari/ ke GUDANG A GUDANG B PABRIK A X 5 12 4 PABRIK B 700 PABRIK C 13 2 9 SUPPLY 6 SELISIH 400 1 700 9 900 1 X 11 3 GUDANG C PERMINTAAN 500 800 700 2000 SELISIH 1 7 3

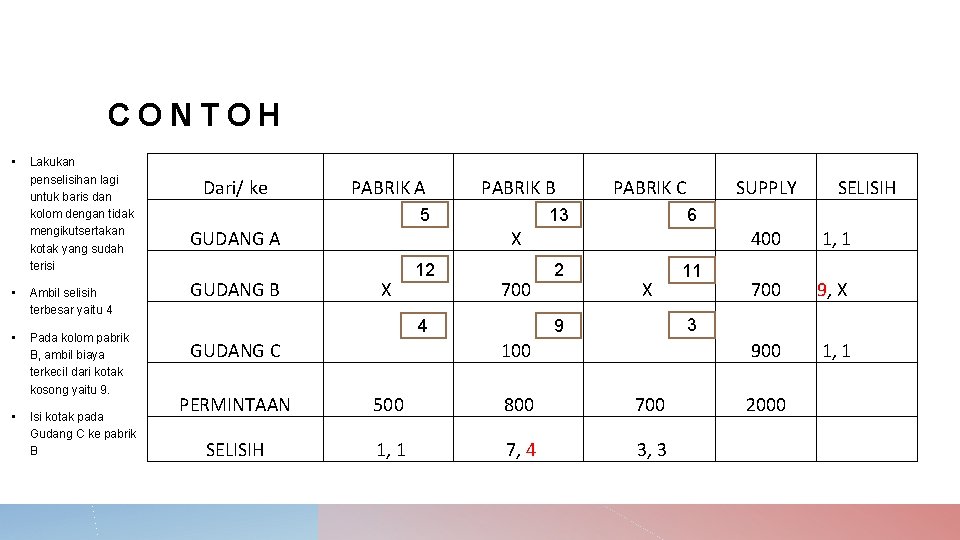
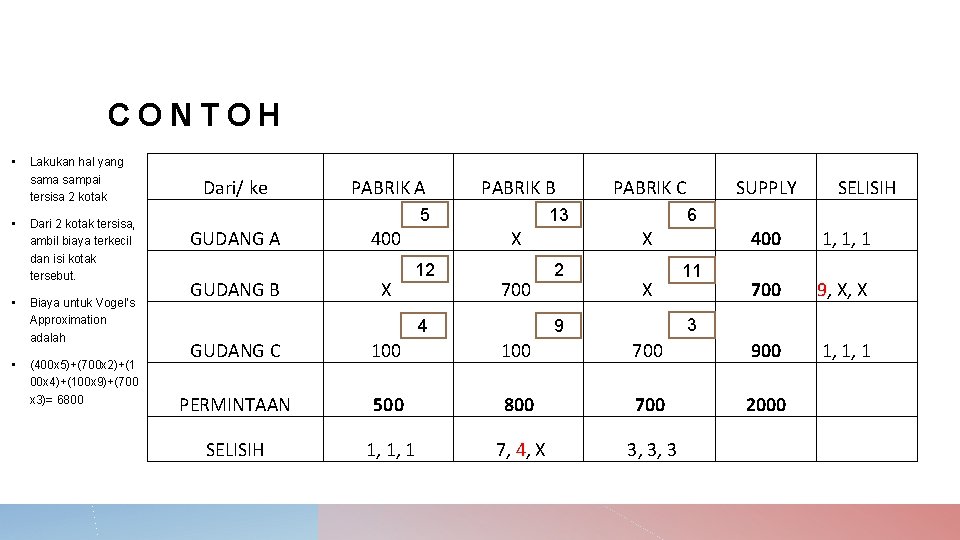
CONTOH • Lakukan penselisihan lagi untuk baris dan kolom dengan tidak mengikutsertakan kotak yang sudah terisi • Ambil selisih terbesar yaitu 4 • Pada kolom pabrik B, ambil biaya terkecil dari kotak kosong yaitu 9. • Isi kotak pada Gudang C ke pabrik B Dari/ ke PABRIK A PABRIK B 5 GUDANG A GUDANG B X 13 X 12 PABRIK C 700 4 SUPPLY 6 2 SELISIH X 11 400 1, 1 700 9, X 3 9 GUDANG C 100 900 1, 1 PERMINTAAN 500 800 700 2000 SELISIH 1, 1 7, 4 3, 3

CONTOH • • Lakukan hal yang sama sampai tersisa 2 kotak Dari 2 kotak tersisa, ambil biaya terkecil dan isi kotak tersebut. Biaya untuk Vogel’s Approximation adalah (400 x 5)+(700 x 2)+(1 00 x 4)+(100 x 9)+(700 x 3)= 6800 Dari/ ke PABRIK A PABRIK B 5 GUDANG A GUDANG B 400 X 13 X 12 PABRIK C 700 4 SUPPLY 6 X 2 SELISIH X 11 400 1, 1, 1 700 9, X, X 3 9 GUDANG C 100 700 900 1, 1, 1 PERMINTAAN 500 800 700 2000 SELISIH 1, 1, 1 7, 4, X 3, 3, 3

UJI OPTIMALITAS • Langkah selanjutnya adalah melakukan uji optimalitas. Langkah ini merupakan langkah penyelesaian model untuk mendapatkan solusi minimal. Pada penelitian ini pengujian optimalitas digunakan dengan menggunakan metode batu loncatan (Stepping Stone Method) dan MODI (Modified Distribution).

STEPPING STONE • Metode Stepping Stone digunakan sebagai pengecekan apakah perhitungan yang telah kita hitung menggunakan solusi transportasi awal sudah benar optimal atau belum

LANGKAH-LANGKAH 1. Lakukan pengecekan terhadap sel-sel yang masih kosong, 2. lakukan penarikan garis, garis bergerak (searah jarum jam/berlawanan) secara lurus ke arah sel yang telah terisi dengan alokasi, tidak boleh diagonal 3. Hanya ada satu jalur tertutup untuk setiap kotak kosong. 4. Jalur harus mengikuti kotak terisi. 5. Baik kotak terisi maupun kotak kosong dapat dilewati dalam penyusunan jalur tertutup. 6. Suatu jalur dapat melintasi dirinya. 7. Sebuah penambahan dan pengurangan yang sama besar harus kelihatan pada setiap baris dan kolom pada jalur itu. 8. Lakukan trial and error

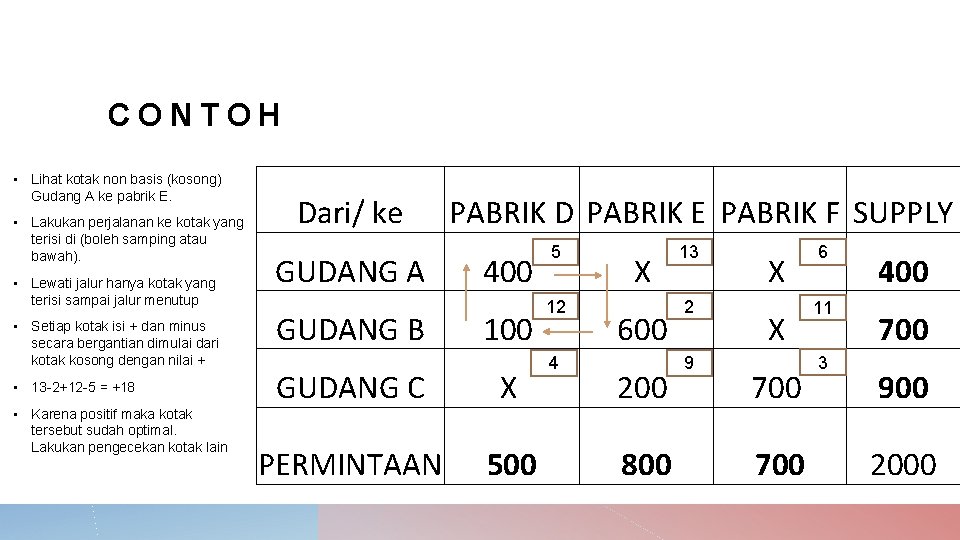
CONTOH • Lihat kotak non basis (kosong) Gudang A ke pabrik E. • Lakukan perjalanan ke kotak yang terisi di (boleh samping atau bawah). • Lewati jalur hanya kotak yang terisi sampai jalur menutup • Setiap kotak isi + dan minus secara bergantian dimulai dari kotak kosong dengan nilai + • 13 -2+12 -5 = +18 • Karena positif maka kotak tersebut sudah optimal. Lakukan pengecekan kotak lain Dari/ ke GUDANG A GUDANG B PABRIK D PABRIK E PABRIK F SUPPLY 400 100 GUDANG C X PERMINTAAN 500 5 12 4 X 600 200 800 13 2 9 X X 700 6 11 3 400 700 900 2000

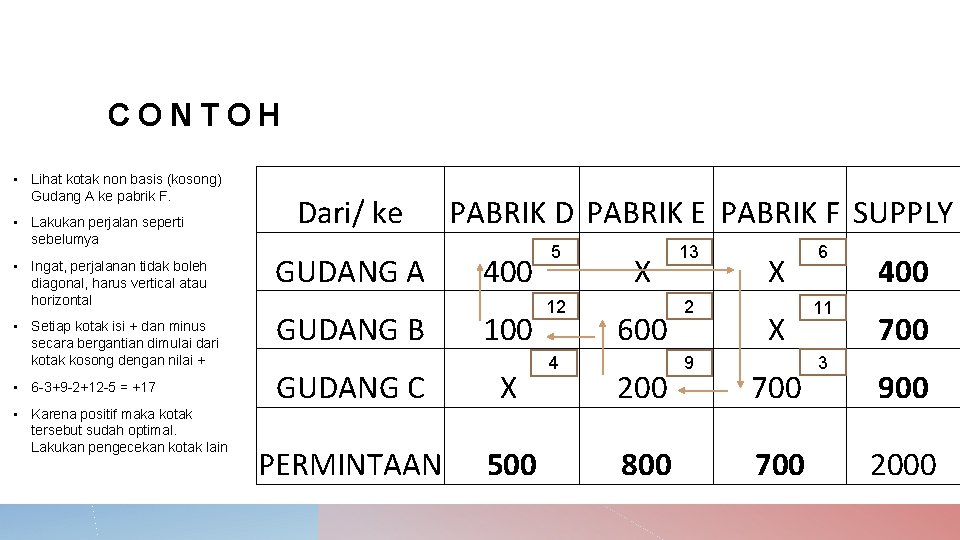
CONTOH • Lihat kotak non basis (kosong) Gudang A ke pabrik F. • Lakukan perjalan seperti sebelumya • Ingat, perjalanan tidak boleh diagonal, harus vertical atau horizontal • Setiap kotak isi + dan minus secara bergantian dimulai dari kotak kosong dengan nilai + • 6 -3+9 -2+12 -5 = +17 • Karena positif maka kotak tersebut sudah optimal. Lakukan pengecekan kotak lain Dari/ ke GUDANG A GUDANG B PABRIK D PABRIK E PABRIK F SUPPLY 400 100 GUDANG C X PERMINTAAN 500 5 12 4 X 600 200 800 13 2 9 X X 700 6 11 3 400 700 900 2000

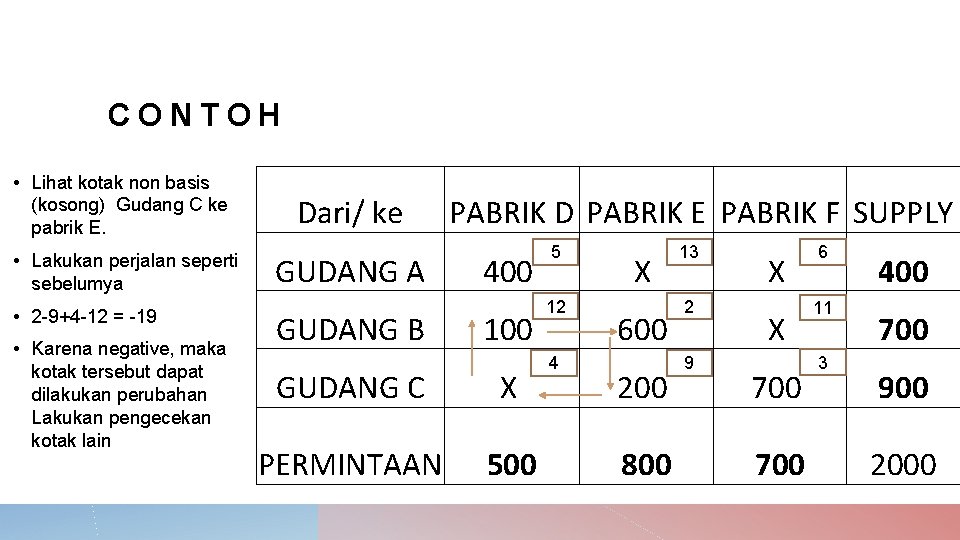
CONTOH • Lihat kotak non basis (kosong) Gudang C ke pabrik E. • Lakukan perjalan seperti sebelumya • 2 -9+4 -12 = -19 • Karena negative, maka kotak tersebut dapat dilakukan perubahan Lakukan pengecekan kotak lain Dari/ ke GUDANG A GUDANG B PABRIK D PABRIK E PABRIK F SUPPLY 400 100 GUDANG C X PERMINTAAN 500 5 12 4 X 600 200 800 13 2 9 X X 700 6 11 3 400 700 900 2000

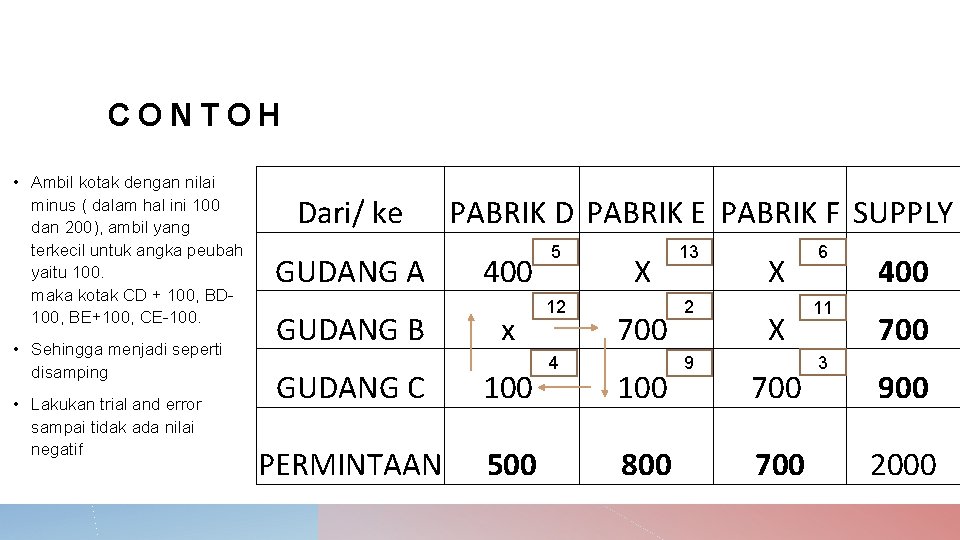
CONTOH • Ambil kotak dengan nilai minus ( dalam hal ini 100 dan 200), ambil yang terkecil untuk angka peubah yaitu 100. maka kotak CD + 100, BD 100, BE+100, CE-100. • Sehingga menjadi seperti disamping • Lakukan trial and error sampai tidak ada nilai negatif Dari/ ke GUDANG A GUDANG B PABRIK D PABRIK E PABRIK F SUPPLY 400 x GUDANG C 100 PERMINTAAN 500 5 12 4 X 700 100 800 13 2 9 X X 700 6 11 3 400 700 900 2000

MODIFIED DISTRIBUTION (MODI) • Metode ini dalam merubah alokasi produk untuk mendapatkan alokasi produksi yang optimal menggunakan suatu indeks perbaikan yang berdasarkan pada nilai baris dan nilai kolom. Cara untuk penentuan nilai baris dan nilai kolom menggunakan persamaan: • Ri + Kj = Cij, dimana : • Ri = Baris ke-i • Kj= Kolom ke j • Cij = biaya pengangkutan 1 unit barang dari sumber I ke tujuan j • Untuk metode MODI ada syarat yang harus dipenuhi, yaitu banyaknya kotak terisi harus sama dengan banyaknya baris ditambah banyaknya kolom dikurang satu.

ALGORITMA MODI 1. Menentukan tabel awal yang fisibel dengan menggunakan metode NW – Corner atau metode ongkos terkecil. 2. Menambahkan variabel Ri dan Kj pada setiap baris dan kolom. 3. Mencari nilai Ri maupun Kj untuk setiap sel basis dengan menggunakan rumus : Ri + Kj = Cij dengan memisahkan salah satu nilai Ri atau Kj sama dengan nol. 4. Menghitung semua nilai sel bukan basis dengan menggunakan rumus Cij – Ri – Ki.

ALGORITMA MODI 5. Menentukan sel yang akan masuk basis dengan memilih nilai sel bukan basis yang memiliki nilai negatif terbesar. Kemudian membuat closed path untuk menentukan sel yang akan keluar dengan memilih jumlah unit terkecil dari sel yang bertanda negatif. 6. Tabel optimum tercapai apabila sel bukan basis semuanya memiliki nilai = 0. 7. Jika tabel belum optimum, kembali ke langkah 2 sehingga ditemukan tabel optimum.

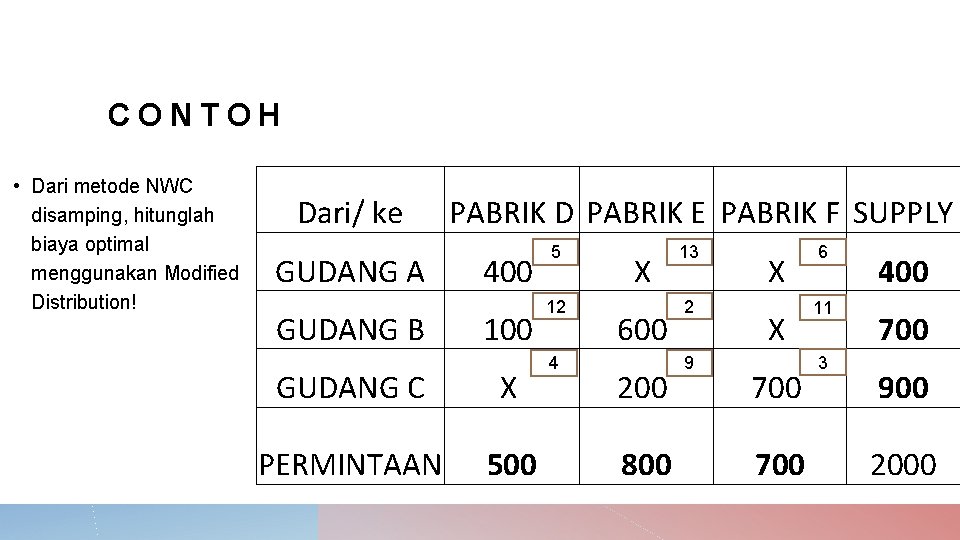
CONTOH • Dari metode NWC disamping, hitunglah biaya optimal menggunakan Modified Distribution! Dari/ ke GUDANG A GUDANG B PABRIK D PABRIK E PABRIK F SUPPLY 400 100 GUDANG C X PERMINTAAN 500 5 12 4 X 600 200 800 13 2 9 X X 700 6 11 3 400 700 900 2000

CONTOH • Cari nilai setiap baris dan kolom dari kotak basis dengan nilai baris pertama = 0 • Ri + Kj = Cij, nilai baris pertama (RA) = 0 o RA + KD = CAD => 0 + KD = 5 => KD = 5 o RB + KD = CBD => RB + 5 = 12 => RB = 7 o RB + KE = CBE => 7 + KE = 2 => KE = -5 o RC + KE = CCE => RC + (-5) = 9 => RC = 14 o RC + KF = CCF => 14 + KF = 3 => KF = -11

CONTOH • Menghitung nilai non basis dengan rumus Cij – Ri – Kj o CAE – RA – KE => 13 – 0 – (-5) = 18 o CAF – RA – KF => 6 – 0 – (-11) = 17 o CBF – RB – KF => 11 – 7 – (-11) = 15 o CCD – RC – KD => 4 – 14 – 5 = -15 • Titik perubahan ada pada nilai minus terbesar yaitu -15 (kotak CD), lakukan perubahan pada kotak CD • Jika semua nilai positif, maka tidak dilakukan perubahan dan biaya sudah optimal, namun jika masih terdapat hasil minus, maka perubahan akan terus dilakukan

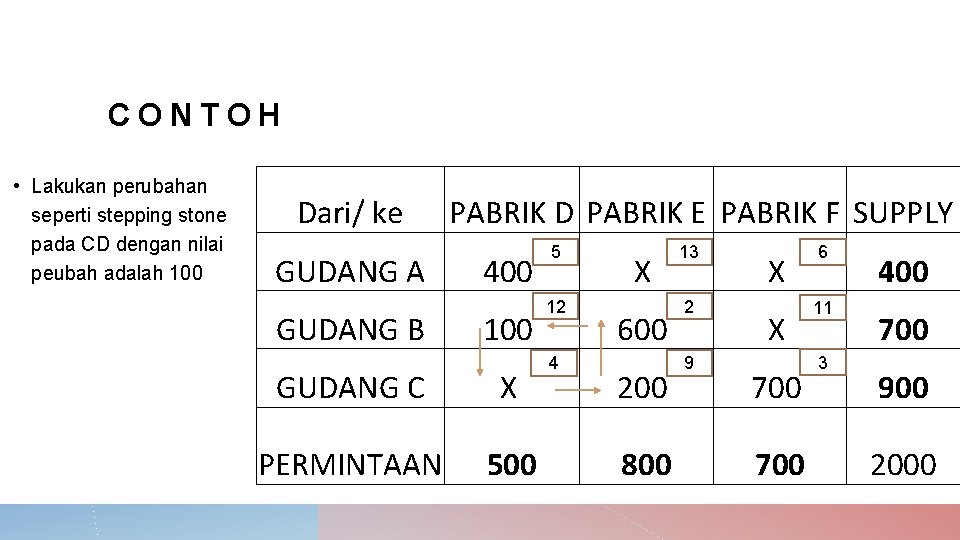
CONTOH • Lakukan perubahan seperti stepping stone pada CD dengan nilai peubah adalah 100 Dari/ ke GUDANG A GUDANG B PABRIK D PABRIK E PABRIK F SUPPLY 400 100 GUDANG C X PERMINTAAN 500 5 12 4 X 600 200 800 13 2 9 X X 700 6 11 3 400 700 900 2000

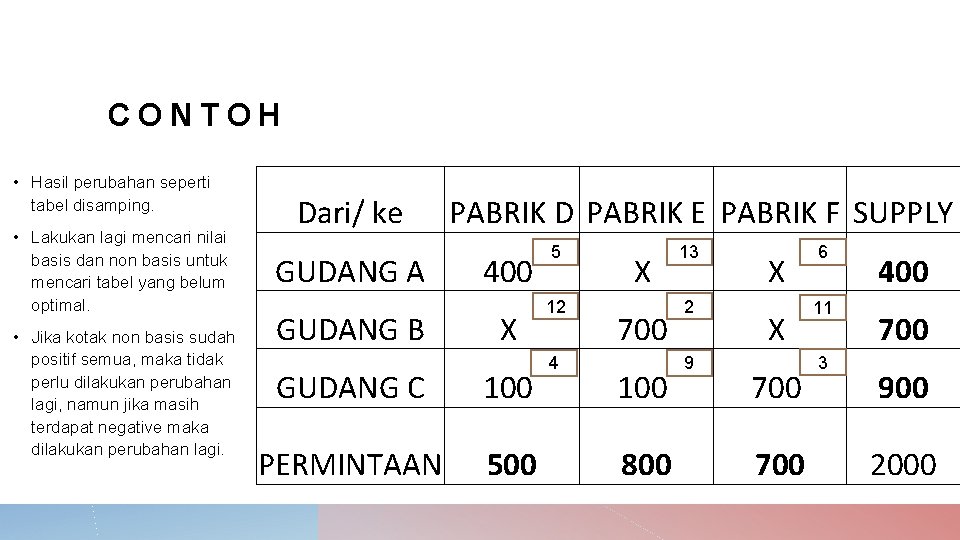
CONTOH • Hasil perubahan seperti tabel disamping. • Lakukan lagi mencari nilai basis dan non basis untuk mencari tabel yang belum optimal. • Jika kotak non basis sudah positif semua, maka tidak perlu dilakukan perubahan lagi, namun jika masih terdapat negative maka dilakukan perubahan lagi. Dari/ ke GUDANG A GUDANG B PABRIK D PABRIK E PABRIK F SUPPLY 400 X GUDANG C 100 PERMINTAAN 500 5 12 4 X 700 100 800 13 2 9 X X 700 6 11 3 400 700 900 2000