Metode Simpleks Program linier bentuk standar Pengantar metode

Metode Simpleks Program linier bentuk standar Pengantar metode simpleks

Program Linier Bentuk Standar (1) �Program linier dapat memiliki �Fungsi tujuan: �Maksimal atau minimum �Fungsi kendala dengan bentuk pertidak samaan: �=, ≤, atau ≥ �Dan variable dapat memiliki batas maupun batas bawah �Program linier bentuk standar: �Fungsi tujuan: maksimum �Fungsi kendala: ≤ �Semua konstanta RHS positif �Semua variable dibatasi pada nilai non-negative

Program Linier Bentuk Standar (2) �Bentuk aljabar untuk sebuah program linier yang memiliki m buah fungsi kendala dan n buah variable, dapat dituliskan seperti berikut ini: �Fungsi tujuan: �m fungsi kendala: �n buah non-negatif, x 1 ≥ 0, x 2 ≥ 0, …, xn ≥ 0.

Metode-metode �Grafis; �Jumlah variable yang sedikit �Simpleks; �Jumlah variable: small - large �Interior-point �Jumlah variable: extra large �Pembahasan difokuskan pada mekanisme metode simpleks: �Terminologi-terminologi �Mekanisme dasar metode simpleks

Definisi �Solution: semua titik yang berada di bidang variable, dapat merupakan titik yang feasible atau infeasible (paling tidak memenuhi satu fungsi kendala). �Corner point solution: terjadi jika dua atau lebih fungsi kendala saling berpotongan. Titik yang dihasilkan disebut sebagai corner point, bisa di dalam atau di luar feasible region. �Feasible corner point: corner point yang berada di dalam feasible region. �Adjacent corner point: dua buah corner point yang dihubungkan oleh bagian garis dari sebuah fungsi kendala.

Sifat-sifat penting Program linier �Titik optimum selalu ada di feasible corner point �hal ini merupakan hasil dari semua fungsi kendala dan fungsi tujuan bersifat linier �Jika sebuah feasible corner point memiliki nilai fungsi tujuan yang lebih besar dari semua adjacent corner point, maka tiitk tersebut dikatakan sebagai titik optimum. �Feasible corner point ada dalam jumlah yang terbatas.

Tahap-tahap metode simpleks (1) �Fase pertama (start-up): tentukan sembarang feasible corner point. �Untuk program linier bentuk standar, titik origin (0, 0) selalu berada dalam feasible region. Jadi, titik (0, 0) adalah titik dimana iterasi metode simpleks akan dimulai. �Untuk program linier bentuk umum, penentuan titik dimana metode simpleks akan mulai sedikit lebih rumit. �Fase kedua (iterasi): secara berulang berpindah ke feasible corner point yang berdekatan sampai tidak ada nilai fungsi tujuan yang lebih baik pada feasibel corner point.

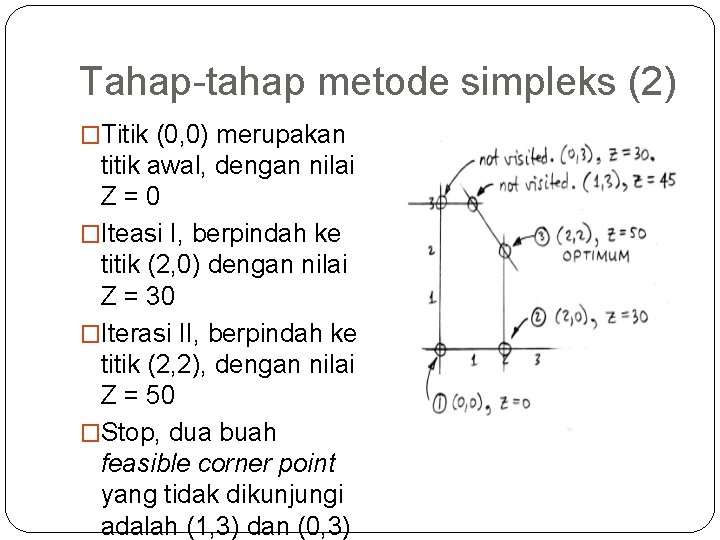
Tahap-tahap metode simpleks (2) �Titik (0, 0) merupakan titik awal, dengan nilai Z=0 �Iteasi I, berpindah ke titik (2, 0) dengan nilai Z = 30 �Iterasi II, berpindah ke titik (2, 2), dengan nilai Z = 50 �Stop, dua buah feasible corner point yang tidak dikunjungi adalah (1, 3) dan (0, 3)

Penentuan Corner Point Secara Aljabar �Dalam penerapannya, program linier dapat memiliki variable ratusan, ribuan bahkan lebih. �Program linier dengan skala besar, corner point ditentukan secara aljabar. �Untuk program linier bentuk standar, dilakukan dengan cara mengkonversi bentuk pertidaksamaan menjadi bentuk persamaan �Kemudian, dengan metode eliminasi gauss dapat ditentukan titik-titik perpotongan antara dua atau lebih fungsi kendala.

Konversi pertidaksamaan ke bentuk persamaan (1) �Konversi dilakukan dengan cara menambahkan sebuah variable, disebut sebagai slack variable. �Nilai slack variable akan selalu berubah untuk menghasilkan persamaan yang benar. �Contoh: �Catatan: slack variable bernilai positif jika sebuah fungsi kendalam keadaan tidak aktif (masih berada di dalam feasible region)

Konversi pertidaksamaan ke bentuk persamaan (2) �Hasil konversi pertidaksamaan ke bentuk persamaan dari suatu program linier: �Pada awalnya, program linier tersebut hanya memiliki dua buah variable yaitu (x 1 dan x 2), setelah dikonversi variable berjumlah 5 bauh, yaitu (x 1, x 2, s 1, s 2, s 3)

Terminologi aljabar �Augmented solution: nilai dengan semua variable, baik variable original dan slack variable �Basic solution: merupakan sebuah augmented corner point solution (bisa feasible atau infeasible) �Basic feasible solution: merupakan sebuah augmented feasible corner point solution. �Catatan: metode simpleks fokus pada basic feasible solution.

Setting nilai variable-variable (1) �Dengan memperhatikan bentuk program linier yang telah dikonversi menjadi persamaan; �Terdapat 5 variable dengan 3 buah persamaan fungsi kendala �Hal ini berarti, dua buah variable ditentukan nilai secara acak, dan variable yang lain dihitung menggunakan 3 persamaan fungsi kendala tersebut. �Jumlah variable yang nilainya dapat ditentukan secara acak disebut sebagai degree of freedom dari program linier tersebut, secara umum: �df = (jumlah variable dalam bentuk persamaan) – (jumlah persamaan fungsi kendala)

Setting nilai variable-variable (2) �Metode simpleks secara otomatis memberikan nilai pada variable-variable df dan menghitung nilai variable-variable yang lain. �Metode simpleks akan memberi nilai nol pada variable-variable df tersebut.

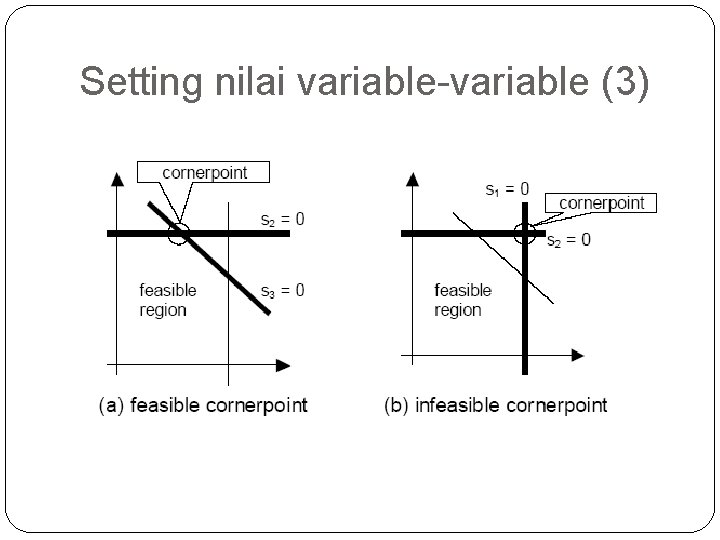
Setting nilai variable-variable (3)

Terminologi metode simpleks �Nonbasic variable: variable yang sedang diberi nilai nol oleh metode simpleks. �Basic variable: variable yang tidak sedang diberi nilai nol oleh metode simpleks. �Basis: variable yang selalu berada pada nonbasic variable atau basic variable selama proses metode simpleks. �Nonbasic, variable bernilai NOL, fungsi kendala yang bersangkutan dalam keadaan aktif.

Iterasi perpindahan titik (1) �Cara yang termudah untuk berpindah dari suatu titik basic feasible solution ke titik basic feasible solution yang lain adalah dengan mencara titik yang berdekatan. �Sifat-sifat titik-titik basic feasible solution yang berdekatan: �Himpunan nonbasic variable sama kecuali satu variable �Himpunan basic variable sama kecuali satu variable �Tiga kondisi yang harus dipenuhi dalam perpindahan ke titik basic feasible solution: �Corner point harus berdekatan �Corner point harus berada di dalam feasible region �Corner point yang baru harus memiliki nilai fungsi

Iterasi perpindahan titik (2) �Penentuan entering basic variable: �Menentukan nonbasic variable yang akan menjadi basic variable. �Dilakukan dengan cara menentukan nonbasic variable manakah yang memberikan pengaruh yang paling besar terhadap perubahan fungsi tujuan. �Penentuan leaving basic variable: �Entering basic variable yang telah ditentukan akan bertambah nilainya sampai sebuah basic variable nilainya menjadi NOL. �Basic variable yang nilainya menjadi NOL tersebut berubah menjadi nonbasic variable.

Minimum Ratio Test (MRT) �Untuk menentukan leaving basic variable pada persamaan fungsi kendala tertentu: �Dua kasus untuk nilai MRT: �Jika koefisien entering basic variable NOL, berarti fungsi kendala tersebut tidak berpotongan dengan fungsi kendala yang masih aktif. �Jika koefisien entering basic variable NEGATIF, bearti fungsi kendala tersebut berpotongan dengan fungsi kendala yang aktif, tetapi arah kenaikan nilai entering basic variable semakin mejauh dari titik perpotongan tersebut.