METODE SIMPLEKS Matematika Sistem Informasi 2 Metode Simpleks

METODE SIMPLEKS Matematika Sistem Informasi 2

Metode Simpleks Penggunaan metode grafik sangat terbatas pada program linear, karena hanya berlaku untuk memecahkan masalah yang mengandung 2 variabel. Jika program linear mengandung 3 atau lebih variabel, maka metode grafik tidak dapat digunakan lagi, sehingga digunakan metode simpleks untuk memecahkan masalah Dalam metode simpleks, diadakan pengubahan pertidaksamaan dengan cara menambahkan variabel slack untuk pertidaksamaan yang mengandung unsur dan mengurangkan variabel surplus untuk pertidaksamaan yang mengandung unsur . (Nababan, 1994)

Contoh Maksimumkan Z = 3 x 1 + 4 x 2 Fungsi kendala 2, 5 x 1 + x 2 20 3 x 1 + 3 x 2 30 x 1 + 2 x 2 16 x 1, x 2 0

Langkah 1 Ø Fungsi tujuan diubah menjadi fungsi implisit Z - 3 x 1 - 4 x 2 = 0 Ø Fungsi kendala diubah dari pertidaksamaan menjadi persamaan dengan menambahkan variabel slack 2, 5 x 1 + x 2 + x 3 = 20 3 x 1 + 3 x 2 + x 4 = 30 x 1 + 2 x 2 + x 5 = 16 x 1, x 2, x 3, x 4, x 5 0

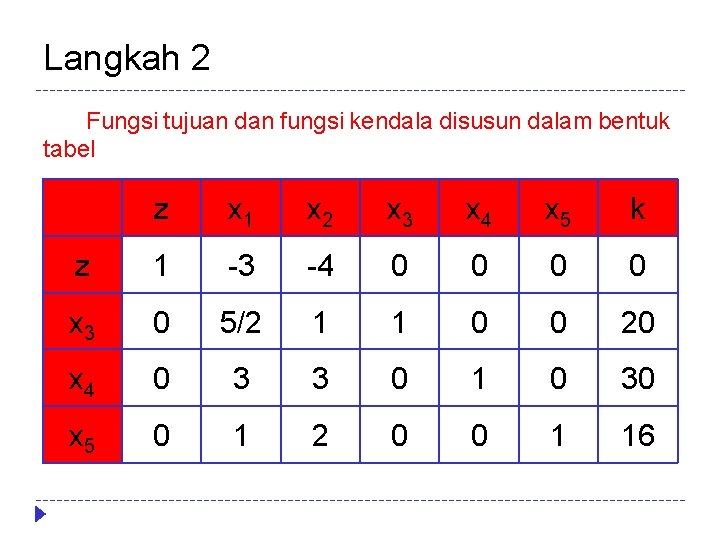
Langkah 2 Fungsi tujuan dan fungsi kendala disusun dalam bentuk tabel z x 1 x 2 x 3 x 4 x 5 k z 1 -3 -4 0 0 x 3 0 5/2 1 1 0 0 20 x 4 0 3 3 0 1 0 30 x 5 0 1 2 0 0 1 16

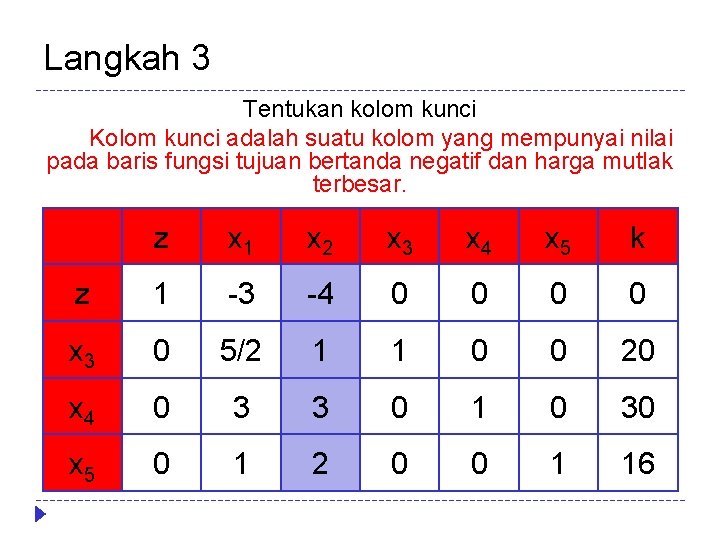
Langkah 3 Tentukan kolom kunci Kolom kunci adalah suatu kolom yang mempunyai nilai pada baris fungsi tujuan bertanda negatif dan harga mutlak terbesar. z x 1 x 2 x 3 x 4 x 5 k z 1 -3 -4 0 0 x 3 0 5/2 1 1 0 0 20 x 4 0 3 3 0 1 0 30 x 5 0 1 2 0 0 1 16

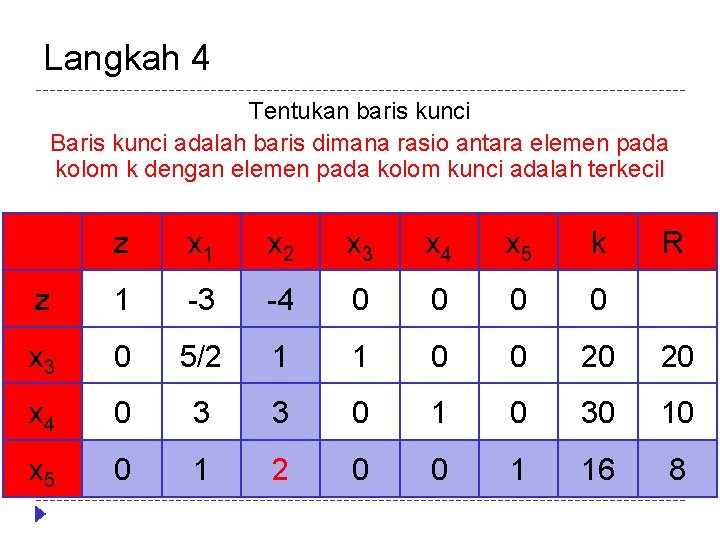
Langkah 4 Tentukan baris kunci Baris kunci adalah baris dimana rasio antara elemen pada kolom k dengan elemen pada kolom kunci adalah terkecil z x 1 x 2 x 3 x 4 x 5 k R z 1 -3 -4 0 0 x 3 0 5/2 1 1 0 0 20 20 x 4 0 3 3 0 1 0 30 10 x 5 0 1 2 0 0 1 16 8

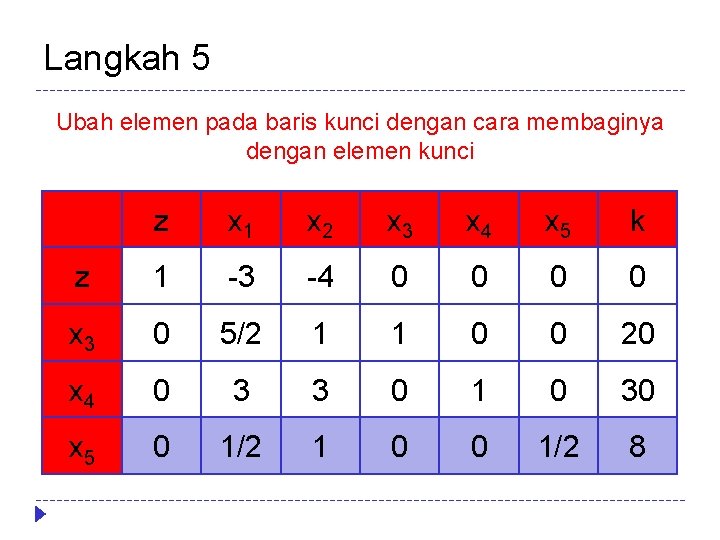
Langkah 5 Ubah elemen pada baris kunci dengan cara membaginya dengan elemen kunci z x 1 x 2 x 3 x 4 x 5 k z 1 -3 -4 0 0 x 3 0 5/2 1 1 0 0 20 x 4 0 3 3 0 1 0 30 x 5 0 1/2 1 0 0 1/2 8

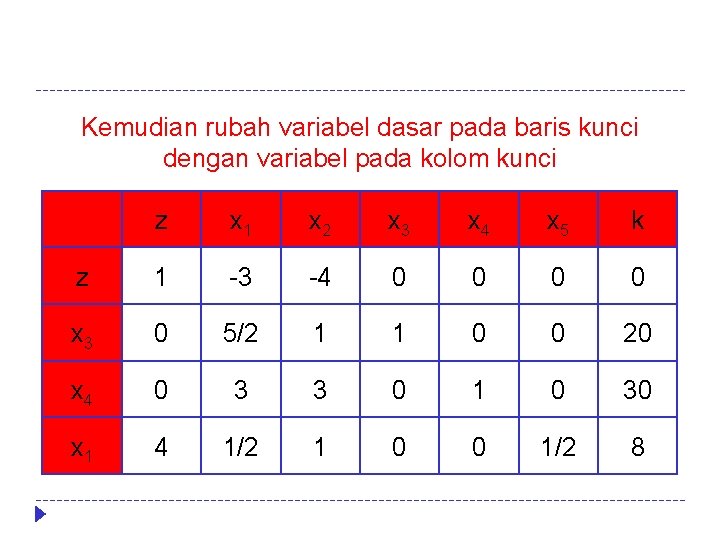
Kemudian rubah variabel dasar pada baris kunci dengan variabel pada kolom kunci z x 1 x 2 x 3 x 4 x 5 k z 1 -3 -4 0 0 x 3 0 5/2 1 1 0 0 20 x 4 0 3 3 0 1 0 30 x 1 4 1/2 1 0 0 1/2 8

Langkah 6 Rubah elemen pada baris lain dengan cara: Elemen pada = baris baru Elemen pada aris lama Z baru = 1 =1 -4 2 * 0 Elemen pada kolom kunci Elemen pada * baris kunci

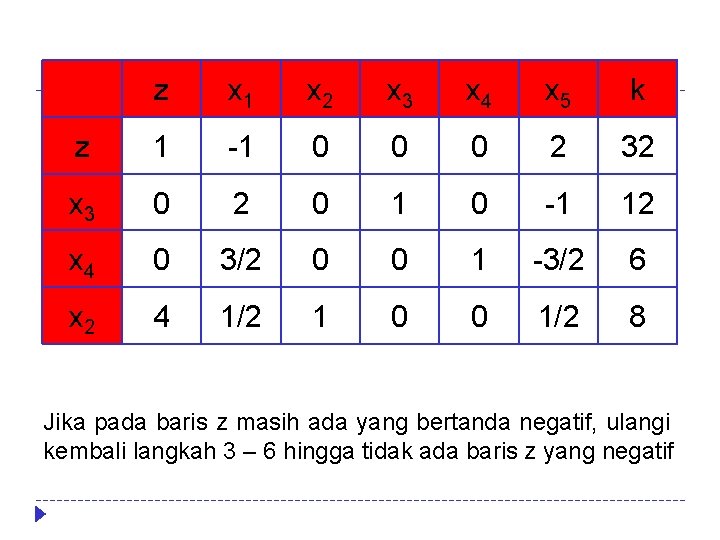
z x 1 x 2 x 3 x 4 x 5 k z 1 -1 0 0 0 2 32 x 3 0 2 0 1 0 -1 12 x 4 0 3/2 0 0 1 -3/2 6 x 2 4 1/2 1 0 0 1/2 8 Jika pada baris z masih ada yang bertanda negatif, ulangi kembali langkah 3 – 6 hingga tidak ada baris z yang negatif

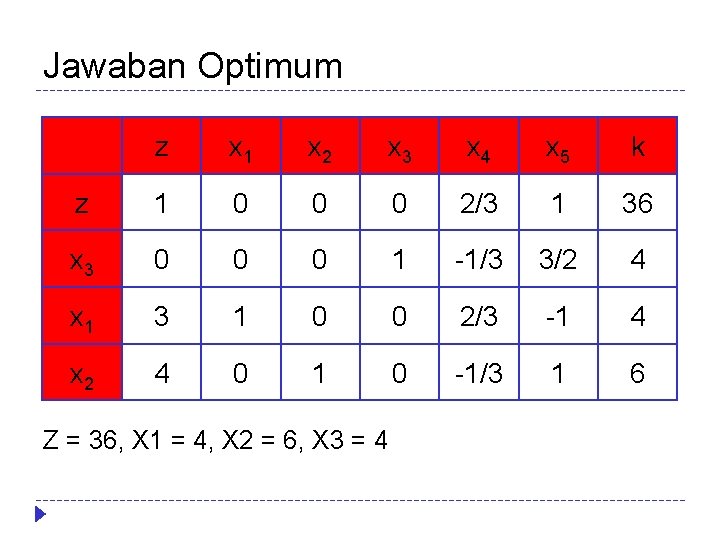
Jawaban Optimum z x 1 x 2 x 3 x 4 x 5 k z 1 0 0 0 2/3 1 36 x 3 0 0 0 1 -1/3 3/2 4 x 1 3 1 0 0 2/3 -1 4 x 2 4 0 1 0 -1/3 1 6 Z = 36, X 1 = 4, X 2 = 6, X 3 = 4