Metode Simpleks Dual dan Kasus Khusus Metode Simpleks

Metode Simpleks Dual dan Kasus Khusus Metode Simpleks Page 1

Pengantar Ide awal digunakan untuk menyelesaikan masalah PL tanpa menggunakan variabel artifisial muncul masalah PL yang tidak memiliki pemecahan dasar yang layak (non-fisibel) = kendala nonnegatif tidak dipenuhi, maka digunakan metode Dual. Simpleks Contoh : minimumkan z = 2 x 1+3 x 2 kendala -x 1+ x 2 ≤-5 3 x 1+ x 2 ≤-6 syarat nonegatif x 1, x 2≥ 0 Page 2

Ketentuan Metode Dual Simpleks 1. Leaving variable adalah variabel basis yang memiliki nilai paling negatif (jika nilainya sama dipilih sembarang). Bila variabel basis sudah positif/nol → proses berakhir (solusi sudah fisibel dan optimal) 2. Entering Variabel dipilih dari variabel non-basis berdasarkan rasio = koefisien persamaan z dibagi dengan koefisien persamaan yang berkaitan dengan baris Leaving Variabel Minimasi : EV = variabel dengan rasio positif terkecil Maksimasi : EV = variabel dengan absolut terkecil Page 3

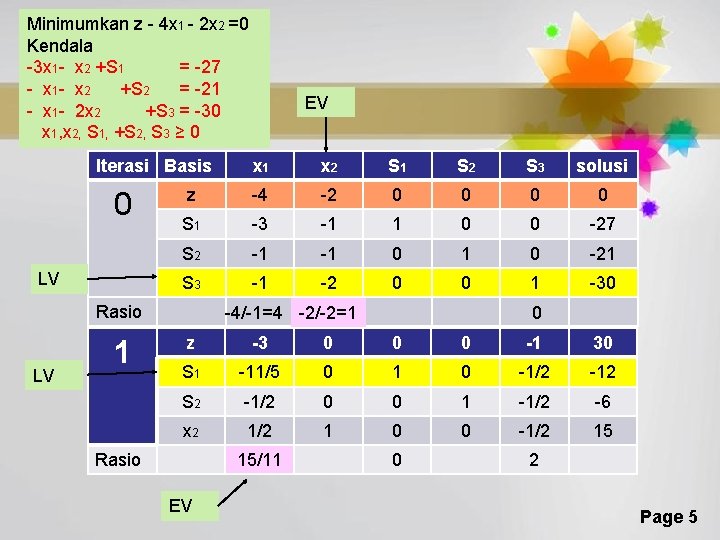
Contoh Minimumkan z = 4 x 1+2 x 2 Kendala 3 x 1+ x 2 ≥ 27 x 1+ x 2 ≥ 21 x 1+2 x 2 ≥ 30 x 1, x 2 ≥ 0 Tidak menggunakan variabel artifisial maka kalikan semua kendala dengan pembatas “≥” dengan -1 maka Minimumkan z = 4 x 1+2 x 2 Kendala -3 x 1 - x 2 ≤ -27 - x 1 - x 2 ≤ -21 - x 1 -2 x 2 ≤ -30 x 1, x 2 ≥ 0 Minimumkan z-4 x 1 -2 x 2 =0 Kendala -3 x 1 - x 2 +S 1 = -27 - x 1 - x 2 +S 2 = -21 - x 1 - 2 x 2 +S 3 = -30 x 1, x 2, S 1, S 2, S 3 ≥ 0 Page 4

Minimumkan z - 4 x 1 - 2 x 2 =0 Kendala -3 x 1 - x 2 +S 1 = -27 - x 1 - x 2 +S 2 = -21 - x 1 - 2 x 2 +S 3 = -30 x 1, x 2, S 1, +S 2, S 3 ≥ 0 Iterasi Basis 0 LV x 1 x 2 S 1 S 2 S 3 solusi z -4 -2 0 0 S 1 -3 -1 1 0 0 -27 S 2 -1 -1 0 -21 S 3 -1 -2 0 0 1 -30 Rasio LV 1 EV -4/-1=4 -2/-2=1 0 z -3 0 0 0 -1 30 S 1 -11/5 0 1 0 -1/2 -12 S 2 -1/2 0 0 1 -1/2 -6 x 2 1/2 1 0 0 -1/2 15 Rasio 15/11 EV 0 2 Page 5

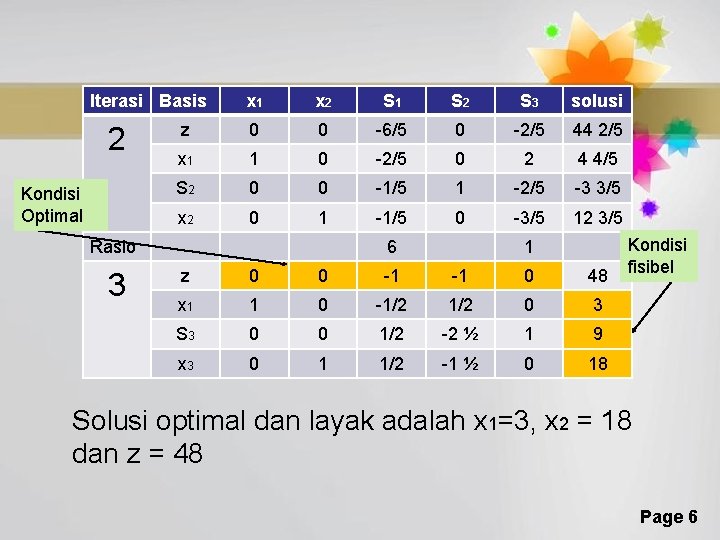
Iterasi Basis 2 Kondisi Optimal x 1 x 2 S 1 S 2 S 3 solusi z 0 0 -6/5 0 -2/5 44 2/5 x 1 1 0 -2/5 0 2 4 4/5 S 2 0 0 -1/5 1 -2/5 -3 3/5 x 2 0 1 -1/5 0 -3/5 12 3/5 Rasio 3 6 1 z 0 0 -1 -1 0 48 x 1 1 0 -1/2 0 3 S 3 0 0 1/2 -2 ½ 1 9 x 3 0 1 1/2 -1 ½ 0 18 Kondisi fisibel Solusi optimal dan layak adalah x 1=3, x 2 = 18 dan z = 48 Page 6

Kasus khusus Metode Simpleks 1. Degenerasi Maksimumkan z = 3 x 1+9 x 2 Kendala x 1 + 4 x 2 ≤ 8 x 1 + 2 x 2 ≤ 4 x 1, x 2 ≥ 0 Iterasi Basis 0 1 2 x 1 x 2 S 1 S 2 solusi z -3 -9 0 0 0 S 1 1 4 1 0 8 S 2 1 2 0 1 4 z -3/4 0 9/4 0 18 x 2 1/4 0 2 S 2 1/2 2 -1/2 1 0 z 0 0 3/2 18 x 2 0 1 1/2 -1/2 2 x 1 1 0 -1 2 0 Muncul 0 pada kolom solusi sehingga ada variabel basis yang bernilai 0 Page 7

Kasus khusus Metode Simpleks 2. Optimum Relatif Maksimumkan z = 2 x 1+4 x 2 Kendala x 1 + 2 x 2 ≤ 5 x 1 + x 2 ≤ 4 Pada x 1, x 2 ≥ 0 variabel Iterasi Basis x 1 x 2 non basis z -2 -4 koefisien fungsi S 1 1 2 tujuannya S 2 1 1 =0 z 0 0 0 1 2 S 1 S 2 solusi 0 0 0 1 0 5 0 1 4 2 0 10 x 2 1/2 1 1/2 0 5/2 S 2 1/2 0 -1/2 1 3/2 z 0 0 2 0 10 x 2 0 1 1 -1 1 x 1 1 0 -1 2 3 x 2=5/2 x 1=0 z=10 x 2=1 x 1=3 z=10 Page 8

Kasus khusus Metode Simpleks 3. Pemecahan Tidak Dibatasi Maksimumkan z = 2 x 1+x 2 Kendala x 1 - x 2 ≤ 10 2 x 1 ≤ 40 x 1, x 2 ≥ 0 Iterasi Basis 0 x 1 x 2 S 1 S 2 solusi z -2 -1 0 0 0 S 1 1 -1 1 0 10 S 2 2 0 0 1 40 Dikolom variabel non basis (x 2) ada nol dan negatif Page 9

Latihan Gunakan metode dual simpleks 1. Minimumkan z = 2 x 1+3 x 2 Kendala 2 x 1 + 2 x 2 ≤ 30 x 1 + 2 x 2 ≥ 10 x 1, x 2 ≥ 0 2. Minimumkan z = 4 x 1+2 x 2 Kendala x 1+x 2 = 1 3 x 1 -x 2 ≥ 2 x 1, x 2 ≥ 0 (Gantikan persamaan dengan dua pertidaksamaan) Page 10

Latihan Tunjukkan PL ini mengalami degenerasi temporer 3. Maksimumkan z = 3 x 1+2 x 2 Kendala 4 x 1 + 3 x 2 ≤ 12 4 x 1 + x 2 ≤ 8 4 x 1 - x 2 ≤ 12 x 1, x 2 ≥ 0 Page 11