Metode Semi Average Setengah ratarata 1 Kasus jumlah










- Slides: 18

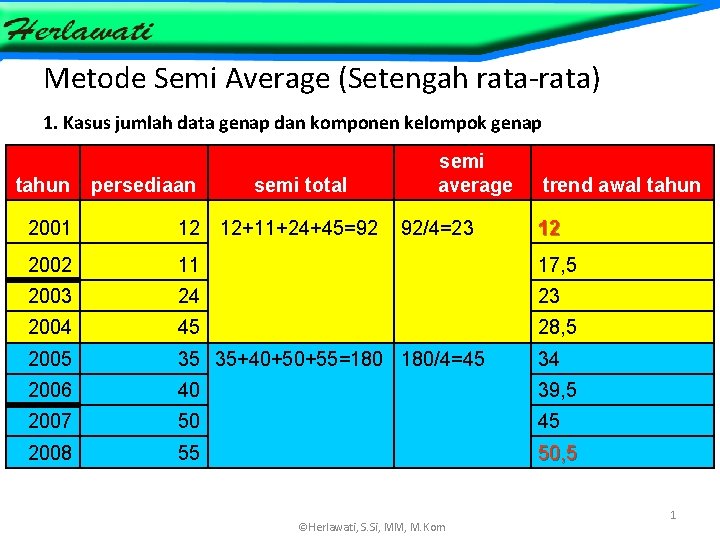
Metode Semi Average (Setengah rata-rata) 1. Kasus jumlah data genap dan komponen kelompok genap tahun persediaan semi total semi average 92/4=23 trend awal tahun 2001 12 12+11+24+45=92 2002 11 17, 5 2003 24 23 2004 45 28, 5 2005 35 35+40+50+55=180 180/4=45 34 2006 40 39, 5 2007 50 45 2008 55 50, 5 ©Herlawati, S. Si, MM, M. Kom 12 1 ©Herlawati, S. Si, MM, M. Kom

Nilai semi average sebesar ao = 23 merupakan nilai trend periode dasar 1 jan 2003 atau 31 des 2002 Nilai semi average sebesar ao = 45 merupakan nilai trend periode dasar 1 jan 2007 atau 31 des 2006 Pertambahan trend tahunan secara rata-rata. Jadi b = (45 -23) / 4= 5, 5 Jadi persamaan trendnya : Y’ = a 0 + bx Jadi persamaan trend dg th dasar 2003 Y’ = 23+5, 5(x) Jadi persamaan trend dg th dasar 2007 Y’ = 45+5, 5(x) ©Herlawati, S. Si, MM, M. Kom 2 ©Herlawati, S. Si, MM, M. Kom

Berapakah persediaan awal tahun 2008, jika diketahui tahun dasar 2007 ? Berapakah persediaan awal tahun 2001, jika diketahui tahun dasar 2007 ? Jawab : Jarak awal tahun 2007 ke awal tahun 2008 : x = 1 persamaan trend dg th dasar 2007 Y’ = 45 + 5, 5 x Y’ = 45+5, 5(1) Y’= 50, 5 x Jarak awal tahun 2007 ke awal tahun 2001 : x = -6 persamaan trend dg th dasar 2007 Y’ = 45 + 5, 5 x Y’ = 45+5, 5(-6) Y’=45+(-33) Y’=12 x ©Herlawati, S. Si, MM, M. Kom 3 ©Herlawati, S. Si, MM, M. Kom

Berapakah persediaan awal tahun 2008, jika diketahui tahun dasar 2003 ? Jawab : Jarak awal tahun 2003 ke awal tahun 2008 : x = 5 persamaan trend dg th dasar 2003 Y’ = 23 + 5, 5 x Y’ = 23+5, 5(5) Berapakah persediaan awal tahun 2001, jika diketahui tahun dasar 2003 ? Jawab : Jarak awal tahun 2003 ke awal tahun 2001 : x = -2 persamaan trend dg th dasar 2003 Y’ = 23 + 5, 5 x Y’=23+5, 5(-2) Y’=23+(-11) Y’=12 x Y’=23+27, 5 x Y’=50, 5 x ©Herlawati, S. Si, MM, M. Kom 4 ©Herlawati, S. Si, MM, M. Kom

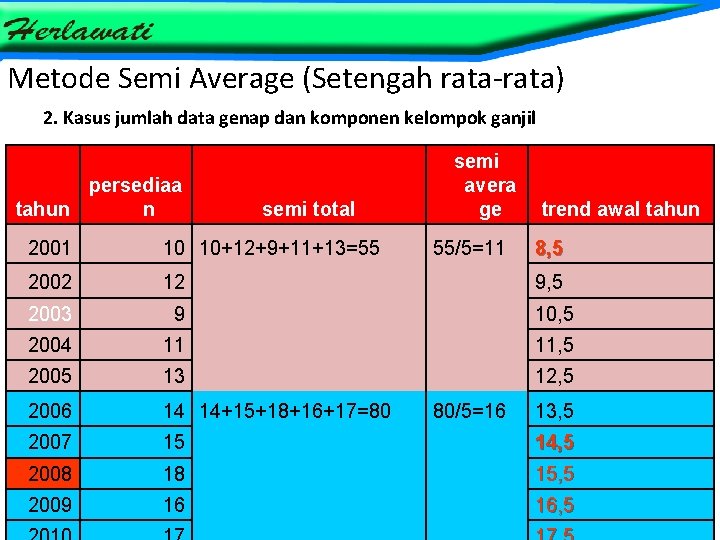
Metode Semi Average (Setengah rata-rata) 2. Kasus jumlah data genap dan komponen kelompok ganjil persediaa tahun n semi avera ge semi total 55/5=11 trend awal tahun 2001 10 10+12+9+11+13=55 2002 12 9, 5 2003 9 10, 5 2004 11 11, 5 2005 13 12, 5 2006 14 14+15+18+16+17=80 2007 15 14, 5 2008 18 15, 5 2009 16 80/5=16 ©Herlawati, S. Si, MM, M. Kom 8, 5 13, 5 16, 5 5 ©Herlawati, S. Si, MM, M. Kom

Nilai semi average sebesar ao = 11 merupakan nilai trend periode dasar 30 juni 2003 Nilai semi average sebesar ao = 16 merupakan nilai trend periode dasar 30 juni 2008 Pertambahan trend tahunan secara rata-rata. Jadi b = 16 -11/5 = 1 Jadi persamaan trendnya : Y’ = a 0 + bx Jadi persamaan trend dg th dasar 2003 Y’ = 11+1 x Jadi persamaan trend dg th dasar 2008 Y’ = 16+1 x ©Herlawati, S. Si, MM, M. Kom 6 ©Herlawati, S. Si, MM, M. Kom

Berapakah persediaan awal tahun 2007, jika diketahui tahun dasar 2008 ? Jawab : Jarak awal tahun 2007 ke bulan juni tahun 2008 : x = -1, 5 persamaan trend dg th dasar 2008 Y’ = 16+ 1(-1, 5) Berapakah persediaan awal tahun 2001, jika diketahui tahun dasar 2008 ? Jawab : Jarak awal tahun 2001 ke bulan juni tahun 2008 : x = -7, 5 persamaan trend dg th dasar 2008 Y’ = 16 + 1 (-7, 5) Y’ = 16+(-7, 5) Y’=8, 5 x Y’ = 16+(-1, 5) Y’= 14, 5 x ©Herlawati, S. Si, MM, M. Kom 7 ©Herlawati, S. Si, MM, M. Kom

Berapakah persediaan awal tahun 2007, jika diketahui tahun dasar 2003 ? Jawab : Jarak awal tahun 2007 ke bulan juni tahun 2003 : x = 3, 5 persamaan trend dg th dasar 2003 Y’ = 11+ 1 x Berapakah persediaan awal tahun 2001, jika diketahui tahun dasar 2003 ? Jawab : Jarak awal tahun 2001 ke bulan juni tahun 2003 : x = -2, 5 persamaan trend dg th dasar 2003 Y’ = 11+ 1 x Y’ = 11+1(-2, 5) Y’=11+(-2, 5) Y’=8, 5 x Y’ = 11+1(3, 5) Y’=11+3, 5 Y’=14, 5 x ©Herlawati, S. Si, MM, M. Kom 8 ©Herlawati, S. Si, MM, M. Kom

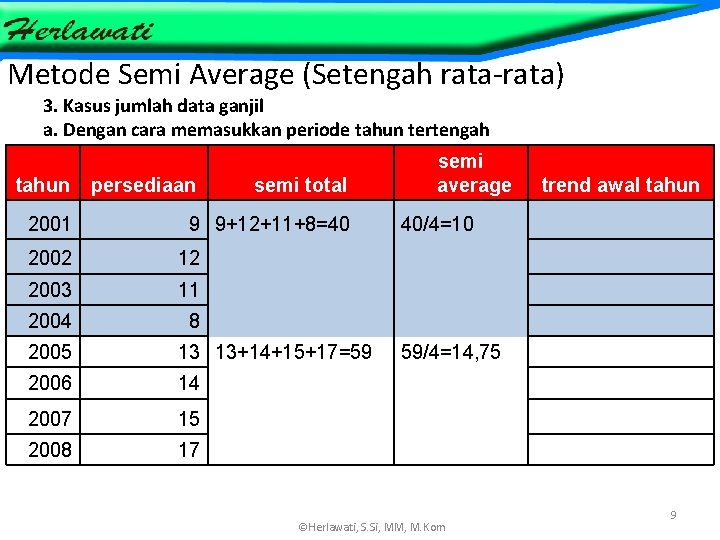
Metode Semi Average (Setengah rata-rata) 3. Kasus jumlah data ganjil a. Dengan cara memasukkan periode tahun tertengah tahun 2001 persediaan semi total 9 9+12+11+8=40 2002 12 2003 11 2004 8 2005 13 13+14+15+17=59 2006 14 2007 15 2008 17 semi average trend awal tahun 40/4=10 59/4=14, 75 ©Herlawati, S. Si, MM, M. Kom 9 ©Herlawati, S. Si, MM, M. Kom

10 ©Herlawati, S. Si, MM, M. Kom

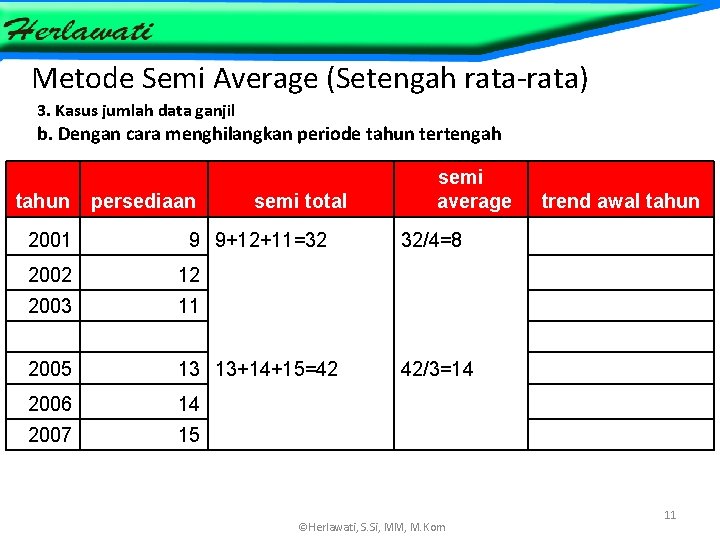
Metode Semi Average (Setengah rata-rata) 3. Kasus jumlah data ganjil b. Dengan cara menghilangkan periode tahun tertengah tahun 2001 persediaan semi total 9 9+12+11=32 2002 12 2003 11 2005 13 13+14+15=42 2006 14 2007 15 semi average trend awal tahun 32/4=8 42/3=14 ©Herlawati, S. Si, MM, M. Kom 11 ©Herlawati, S. Si, MM, M. Kom

12 ©Herlawati, S. Si, MM, M. Kom

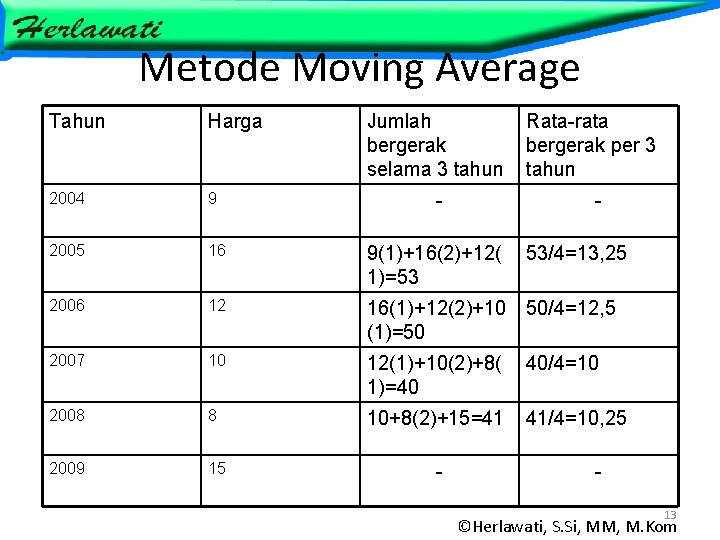
Metode Moving Average Tahun Harga Jumlah bergerak selama 3 tahun 2004 9 2005 16 9(1)+16(2)+12( 1)=53 53/4=13, 25 2006 12 16(1)+12(2)+10 (1)=50 50/4=12, 5 2007 10 12(1)+10(2)+8( 1)=40 40/4=10 2008 8 10+8(2)+15=41 41/4=10, 25 2009 15 - - Rata-rata bergerak per 3 tahun - 13 ©Herlawati, S. Si, MM, M. Kom

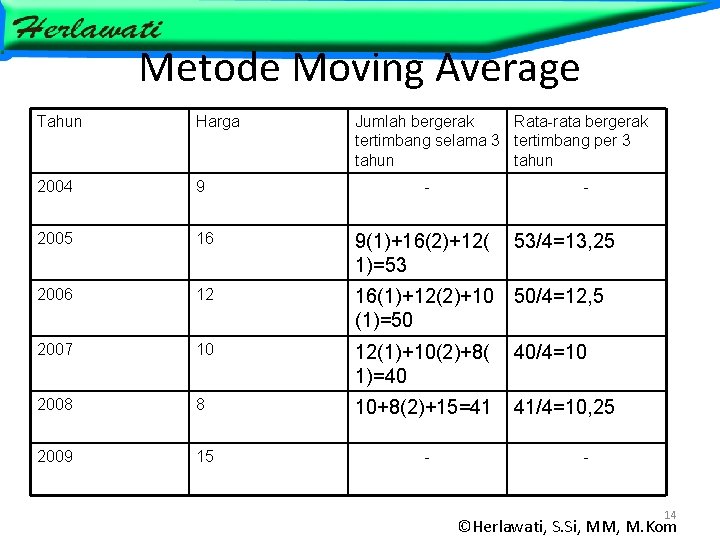
Metode Moving Average Tahun Harga Jumlah bergerak Rata-rata bergerak tertimbang selama 3 tertimbang per 3 tahun 2004 9 2005 16 9(1)+16(2)+12( 1)=53 53/4=13, 25 2006 12 16(1)+12(2)+10 (1)=50 50/4=12, 5 2007 10 12(1)+10(2)+8( 1)=40 40/4=10 2008 8 10+8(2)+15=41 41/4=10, 25 2009 15 - - 14 ©Herlawati, S. Si, MM, M. Kom

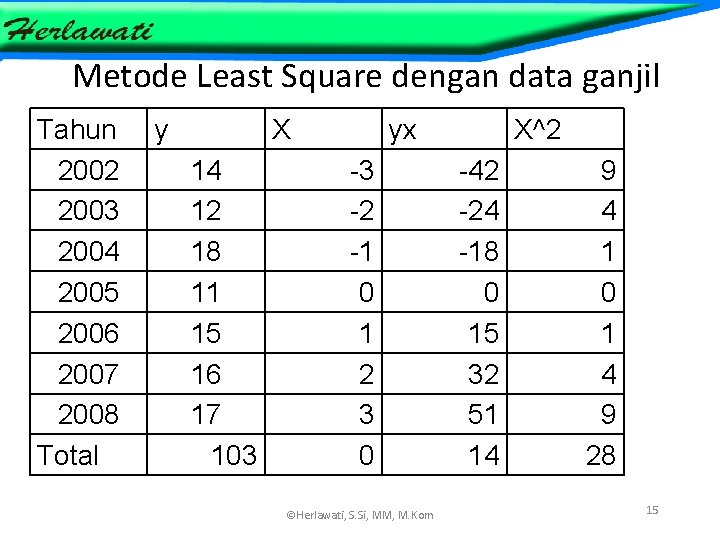
Metode Least Square dengan data ganjil Tahun 2002 2003 2004 2005 2006 2007 2008 Total y X 14 12 18 11 15 16 17 103 yx -3 -2 -1 0 1 2 3 0 ©Herlawati, S. Si, MM, M. Kom X^2 -42 -24 -18 0 15 32 51 14 9 4 1 0 1 4 9 28 15 ©Herlawati, S. Si, MM, M. Kom

16 ©Herlawati, S. Si, MM, M. Kom

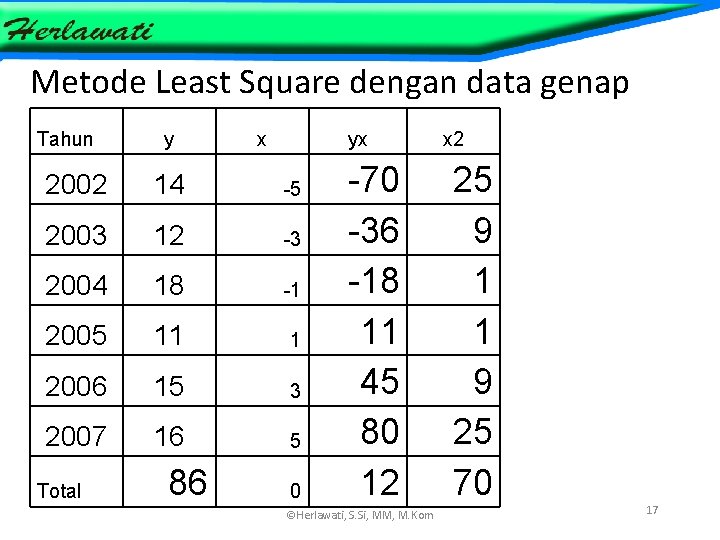
Metode Least Square dengan data genap Tahun y x yx 2002 14 -5 2003 12 -3 2004 18 -1 2005 11 1 2006 15 3 2007 16 5 Total 86 0 -70 -36 -18 11 45 80 12 ©Herlawati, S. Si, MM, M. Kom x 2 25 9 1 1 9 25 70 17 ©Herlawati, S. Si, MM, M. Kom

18 ©Herlawati, S. Si, MM, M. Kom