Metode Numerik Kontrak Perkuliahan dan Pengenalan Metode Numerik

Metode Numerik Kontrak Perkuliahan dan Pengenalan Metode Numerik

Indentitas Mata Kuliah • Nama Mata Kuliah : Metode Numerik • Kode Mata Kuliah : IF 34221 • Kredit : 3 SKS • Semester : IV • Jurusan : Teknik Informatika/S 1

Deskripsi Mata Kuliah • Membahas tentang konsep dasar komputasi yang mengandung kesalahan dan mempelajari metode-metode komputasi untuk penyelesaian masalah persamaan non linear, persamaan linear simultan, interpolasi dan integral numerik.

Referensi • Chapra, Steven, Applied Numerical Method with Matlab for Engineers & Scientist, Mc Grawhill, 2012. • Munir, Rinaldi, Metode Numerik, Penerbit Informatika, Bandung, 2004. • H. Mathews. , John, Numerical Methods for using Matlab, Prentice-hall Inc. , 1999. • Kiusalaas, Jaan, Numerical Method in Engineering with Matlab, Cambridge University Press, 2005. • Nakamura, Shoichiro, Applied Numerical Methods With Software, Prentice-Hall Inc, 1991.

Aturan Perkuliahan • Kehadiran minimal perkuliahan adalah 80 % dari total pertemuan di kelas, kecuali sakit atau ijin tertulis. • Tidak ada ujian perbaikan. Ujian susulan hanya diijinkan jika ada ijin autentik yang bisa ditunjukkan setelah ujian. • Mahasiswa yang terlambat lebih dari 15 menit tidak diperkenankan masuk ke kelas, demikian juga dosen, kecuali telah disepakati sebelumnya. • Tugas masuk tepat waktu, toleransi keterlambatan penyerahan tugas hanya satu hari dengan nilai dikurangi 20 • NA: 10% kehadiran + 30% Tugas atau Quis + 30% UTS + 30% UAS

Materi yang akan dipelajari 1. Deret Taylor, Pendekatan dan Kesalahan 2. Persamaan Non Linier *Metode Biseksi *Metode Regula Falsi *Metode Iterasi Ttk Tetap *Metode Newton Raphson *Metode Sekan 3. Sistem Persamaan Linier Simultan *SPL *Metode Eliminasi Gaus *Sistem Persamaan Linier *Simultan Metode Gauss Jordan *Metode Dekomposisi LU *Iterasi Jacobi *Iterasi Gauss-Seidel

Materi yang akan dipelajari 4. Penyajian Fungsi & 5. Interpolasi Polinomial *Interpolasi Lagrange *Interpolasi Newton Selisih Terbagi *Interpolasi Newton Menggunakan Tabel Selisih Terbagi *Interpolasi Newton Greogry Maju *Interpolasi Newton Greogy Mundur Integral Numerik *Metode Empat Persegi Panjang *Metode Trapesium *Metode Midpoint *Metode 1/3 Simpson *Metode 3/8 Simpson *Metode Kwadratur Gauss

Yang Diperlukan selama perkuliahan Metnum • Kalkulator • Aplikasi Matlab • Pascal • Prasyarat : Kalkulus • TAMBAHAN : telah mengambil Alpro & ALIM sangat membantu • Pembagian kelompok terdiri dari 3 orang.

Alat penyelesaian masalah matematis (Sulit secara analitis) Paket Program (Perlu pengetahuan dasar metnum) Merancang aplikasi tanpa harus membeli Sarana belajar pemrograman komputer Memperkuat pengertian matematika Mengapa perlu mempelajar i Metode Numerik ?

Pengertian Metode Numerik Teknik untuk memformulasikan masalah matematis agar dapat diselesaikan dengan operasi perhitungan dan logika

Metode Numerik Vs Metode Analitik • Selalu Angka • Solusi dalam bentuk fungsi matematika yang dievaluasi menghasilkan nilai dalam bentuk angka • Menghampiri solusi sejati, dibuat seteliti mungkin ( ada error/galat) • Solusi sejati/eksak tidak selalu ditemukan/dapat dihitung

Tahap – tahap Memecahkan Masalah dengan Numerik • Pemodelan masalah dunia nyata ke persamaan matematika • Penyederhanaan model → mengabaikan beberapa variabel/parameter • Formulasi Numerik üTentukan metode numerik yang akan dipakai (teliti, mudah diprogram, waktu eksekusi cepat dan tidak peka terhadap perubahan data cukup kecil. üMenyusun algoritma dari metode numerik yang dipilih • Pemrograman → menerjemahkan ke salah satu bahasa pemrograman • Operasional program dijalankan dengan data uji coba • Evaluasi bandingkan hasil run dengan prinsip dasar/hasil empiris

Deret Taylor • Tools untuk menurunkan metode numerik • Definisi Andaikan f dan f ΄, f ΄΄, … kontinu pada selang [a, b]. Misalkan x 0 ∈ [a, b] maka untuk x disekitar x 0, x ∈ [a, b] maka f(x) dapat diekspansi ke dalam deret Taylor menjadi Jika x - x 0 = h maka deret Taylor dituliskan kembali menjadi Jika x 0 =0 maka deret Taylor ini disebut dengan deret Maclaurin

Contoh • Hampiri fungsi x 0=1 ke dalam deret Taylor disekitar

Latihan 1. Dengan menggunakan deret taylor hampiri fungsi dan disekitar x 0=1 2. Dengan menggunakan deret Maclaurin hampiri fungsi dan 3. Hitung nilai dengan hampiran deret taylor sampai suku ke 4 dan deret Maclaurin untuk x = 0, 4. Bandingkan kedua hasil tersebut dengan perhitungan langsung nilai f(x) untuk x=0, 4. Yang manakah yang lebih teliti? Soal 3 Deret Taylor yang terpotong dengan orde 4

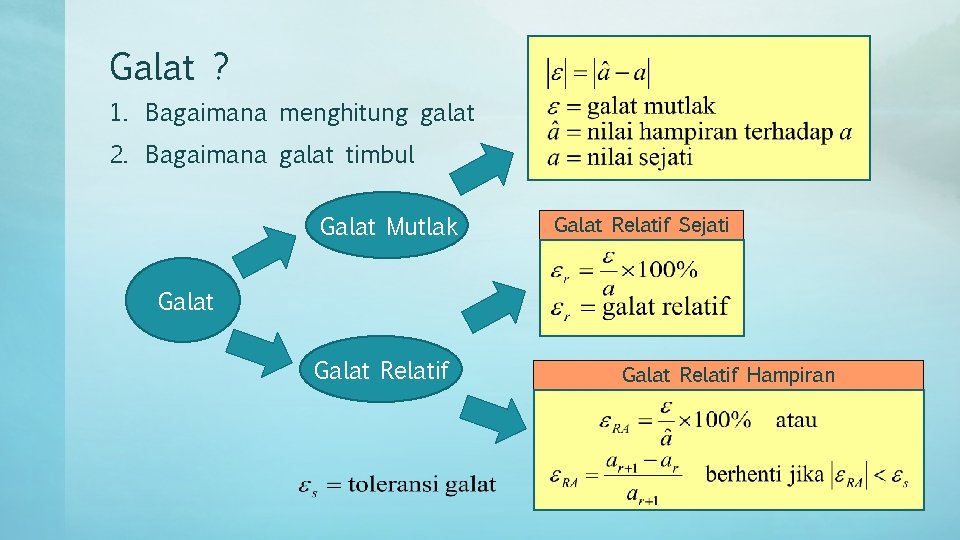
Galat ? 1. Bagaimana menghitung galat 2. Bagaimana galat timbul Galat Mutlak Galat Relatif Sejati Galat Relatif Hampiran

Contoh • Misalkan ada prosedur iterasi Hentikan kondisi jika xi x 1 x 2 Nilai xi (7 desimal) dengan Galat Relatif Hampiran

Sumber Utama Galat • Galat Pemotongan (truncation error) Timbul akibat penggunaan hampiran sebagai pengganti formula eksak → bergantung pada metode komputasi sering disebut Galat Metode • Galat Pembulatan (round-off error) Keterbatasan komputer dalam menyajikan bilangan riil contoh : 1/6 dengan 0, 166667

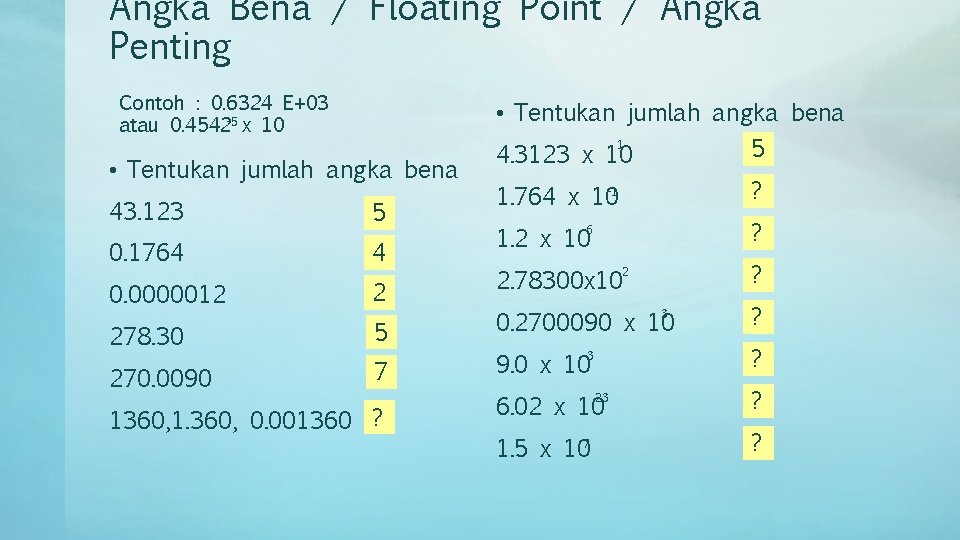
Angka Bena / Floating Point / Angka Penting Contoh : 0. 6324 E+03 atau 0. 4542 -5 x 10 • Tentukan jumlah angka bena 43. 123 5 0. 1764 4 0. 0000012 2 278. 30 270. 0090 • Tentukan jumlah angka bena 1 5 4. 3123 x 10 ? -1 1. 764 x 10 ? -6 1. 2 x 10 ? 2. 78300 x 10 2 5 0. 2700090 x 10 ? 7 9. 0 x 10 ? 1360, 1. 360, 0. 001360 ? 3 -3 6. 02 x 10 ? 1. 5 x 107 ? 23

Orde Hampiran • f(x) diganti dengan fungsi hampiran. Cara mengungkapkan ketelitian penghampiran adalah dengan menggunakan big O • Misalkan f(h) dihampiri dengan fungsi p(h). n Jika |f(h)-p(h)|≤ M|h | dengan M konstanta riil>0 nmaka p(h) menghampiri f(h) dengan orde penghampiran O(h ) dan ditulis n n f(h)=p(h)+O(h ) orde galat dari penghampiran fungsi, umumnya h<1 maka makin besar pangkat makin kecil galat dan semakin teliti penghampiran fungsinya.

Contoh Pada latihan 1 tuliskan kembali orde penghampiran fungsi dengan menggunakan

Contoh Galat Akhir Galat Pemotongan Galat Pembulatan Dengan orde hampiran adalah. . . . Hasil akumulasi dari galat pemotongan dan galat pembulatan

Minggu depan • Bawa Kalkulator • Pelajari pengantar Matlab di ebook Steven Chapra Bab 2 & 3 • Pascal • Matlab