Metode Numerik Analisa Galat Deret Taylor Teknik InformatikaUnitomo















- Slides: 16

Metode Numerik Analisa Galat & Deret Taylor Teknik Informatika-Unitomo Anik Vega Vitianingsih

TEORI KESALAHAN (GALAT) -Penyelesaian numerik dari suatu persamaan matematik hanya memberikan nilai perkiraan yang mendekati nilai eksak (yang benar) dari penyelesaian analitis -Penyelesaian numerik tersebut terdapat kesalahan (galat) terhadap nilai eksak -Keandalan suatu nilai numerik dapat ditandai memakai konsep Angka Bena yaitu angka yang dapat dipergunakan dengan pasti.

Angka ini diperoleh dari sejumlah angka tertentu ditambah dengan satu taksiran. Konsep angka bena mempunyai dua terapan yaitu : 1. Kriteria untuk memerinci seberapa jauh hampiran (aproksimasi) tersebut dapat dipercaya. 2. Tidak menyatakan bilangan tertentu seperti p, e, atau Å7 secara eksak berhingga bilangan. memakai Contoh : Å7 = 2, 645751311…. . sejumlah

Macam – macam kesalahan �Kesalahan Bawaan ◦ Merupakan kesalahan dari nilai data ◦ Kesalahan terjadi karena kekeliruan dalam menyalin data ◦ Kesalahan dalam membaca skala ◦ kesalahan karena kurangnya pengertian mengenai hukum - hukum fisik dari data yang diukur �Kesalahan Pemotongan ◦ Kesalahan terjadi karena tidak dilakukannya perhitungan sesuai dengan prosedur matematik yang benar

�Kesalahan Pembulatan ◦ kesalahan terjadi karena tidak diperhitungkannya beberapa angka terakhir dari suatu bilangan v Bilangan perkiraan digunakan sebagai pengganti bilangan eksak v Suatu bilangan dibulatkan pada posisi ke n dengan membuat semua angka di sebelah kanan dari posisi tersebut nol, sedang angka pada posisi ke n tersebut tidak berubah atau dinaikkan satu digit yang tergantung apakah nilai tersebut lebih kecil atau lebih besar dari setengah dari angka posisi ke n

Pengabaian diluar angka bena yang terjadi karena kesalahan – kesalahan tersebut dikenal dengan galat. Galat terbagi menjadi : 1. Galat pembulatan (untuk menyatakan bilangan eksak) 2. Galat pemotongan (untuk menyatakan prosedure matematis).

Galat yang berhubungan dengan perhitungan / pengukuran dicirikan: - ketelitian (merupakan nilai sejati yang dihitung) - ketepatan (merupakan banyaknya angka bena yang menyatakan suatu nilai atau sebaran dalam perhitungan berulang atau pengukuran nilai yang teliti) sehingga : Nilai sejati = aproksimasi + galat (Et) Dimana : Et = galat sejati = Nilai sejati – aproksimasi

galat x 100 % % Galat relat if (e ) = nilai Dimana: -t : nilai sejati -a : aproksimasi - Ea : galat aproksimasi sekarang – aproksimasi sebelumnya

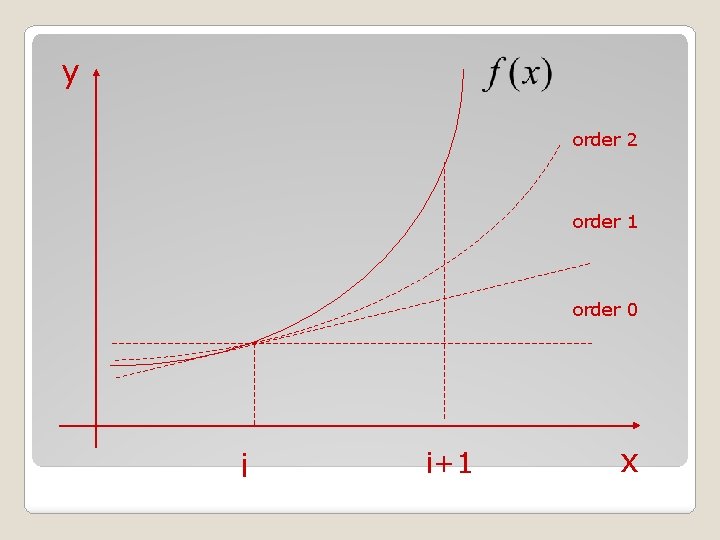
Deret Taylor • Mrk penyelesaian persamaan Diferensial Jika suatu fungsi ƒ(X) diketahui dititik Xi dan semua turunan dari ƒ terhadap X diketahui pada titik tersebut deret Taylor dinyatakan nilai ƒ pada titik Xi+1 yang terletak pada jarak ∆X dari titik Xi. •

1. Memperhitungkan satu suku pertama (order 0) 2. Memperhitungkan dua suku pertama (order 1) 3. Memperhitungkan tiga suku pertama (order 2) 4. Iterasi akan berhenti jika Rn = 0

y order 2 order 1 order 0 i i+1 x

Persamaan deret Taylor: Ket: ƒ(Xi) ƒ(Xi+1) ƒ’, ƒ’’ … ƒn ∆X Rn ! : fungsi dititik 1 : fungsi dititik i+1 : turunan pertama, kedua, …, ke n : jarak antara ƒ(Xi) dan ƒ(Xi+1) : kesalahan pemotongan : operator faktorial

c/: Diketahui seuatu fungsi : dengan menggunakan Deret Taylor pada order berapa, hasil penyelesaian numerik sama dengan penyelesaian eksak? dimana order 0, 1, 2 dan 3 perkiraan fungsi tersebut pada titik xi+1 = 1 & titik xi+1 =1 berada pada jarak=1 dari titik x = 0. Jawab : f(0) = 0. 5 f(1) = 1. 5

Untuk order 0 : f(xi+1) = f(xi) f(0 +1) = f(0) f(1) = 0. 5 Kesalahan pemotongan : Rn = 1. 5 – 0. 5 = 1 Untuk order 1 : f(xi+1)= f(xi) + f’(xi) ∆X /1! f(0+1) = 0. 5 +( )1 = 0. 5 (0. 75 (0) + 0 +0. 25 = 0. 75 Kesalahan pemotongan Rn = 1. 5 – 0. 75 = 0. 75

Untuk Order 2 : f(xi+1) = 0. 5 + 0. 25 * 1 + 1 * (1/2) = 1. 25 Kesalahan pemotongan: Rn = 1. 5 – 1. 25 = 0. 25 Untuk Order 3 : f(xi+1) = 0. 5 + 0. 25 = 1. 5 Kesalahan pemotongan : Rn = 1. 5 – 1. 5 = 0 (terbukti)

Algoritma: 1. Tentukan order dari deret Taylor 2. Masukkan nilai x 0 kedalam rumus deret Taylor 3. Gabungkan semua perhitungan deret Taylor - looping sebanyak i=0; i= ƒ(Xi+1) - if (i==0) Rn=ƒ(x) else if ((i+1)%2==0) Rn=0 else if ((i+1)%2!=0 && (i+1)!=1) Rn=i
 Deret taylor
Deret taylor Angka bena adalah
Angka bena adalah Macam macam galat
Macam macam galat Galat relatif adalah
Galat relatif adalah Angka bena adalah
Angka bena adalah Galat absolut
Galat absolut Jenis jenis galat
Jenis jenis galat Metode numerik teknik informatika
Metode numerik teknik informatika Metode tertutup metode numerik
Metode tertutup metode numerik Contoh soal biseksi
Contoh soal biseksi Algoritma metode euler
Algoritma metode euler Baris dan deret
Baris dan deret Taylor series error
Taylor series error Bentuk umum deret taylor
Bentuk umum deret taylor Deret taylor dan maclaurin
Deret taylor dan maclaurin 0,000454 memiliki …. angka penting
0,000454 memiliki …. angka penting Contoh soal metode clapeyron
Contoh soal metode clapeyron