Metode Euler Definisi Ide dasar penggunaan teknik numerik

Metode Euler

Definisi • Ide dasar penggunaan teknik numerik untuk menyelesaikan persoalan fisika adalah bagaimana menyelesaikan persoalan fisika dengan karakteristik non linear dengan hanya menggunakan operasi hitungan sehingga soal serumit apapun dapat diselesaikan dengan mudah

Contoh analisis • jika nilai y pada ukuran waktu i diketahui maka kita dapat menentukan nilai y berikutnya pada ukuran waktu berikutnya yaitu pada ukuran waktu i+1 sebanyak ukuran waktu yang dikehendaki.

Representasi Grafik Metode Euler

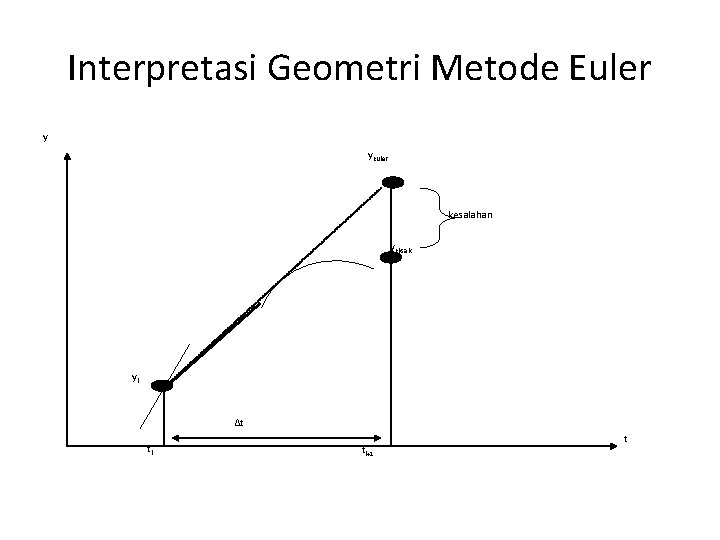
Interpretasi Geometri Metode Euler y y. Euler kesalahan y. Eksak yi ∆t ti ti+1 t

Berdasarkan teori Euler bagaimana solusi numerik untuk kecepatan dan posisi? • • Dengan cara yang sama akan diperoleh • • dimana menyatakan fungsi turunan keduanya.

Contoh aplikasi metode Euler • Berikut disajikan contoh analisis gerak jatuh dengan menghitung pengaruh gesekan udara mudara= ρAvdt

• gerak jatuh karena pengaruh adanya gesekan dapat dituliskan sebagai

Diagram Gaya pada Benda yang Jatuh dalam Suatu Fluida FA m FB

Solusi persamannya

Contoh soal numerik Tentukan percepatan, kecepatan dan posisi dari gerak jatuh dengan menggunakan Spreadsheet untuk benda berbentuk bola yang memiliki rmassa 0, 02 kg jari-jari 0, 01 m dan C = 0, 46.

Variabel persamaan

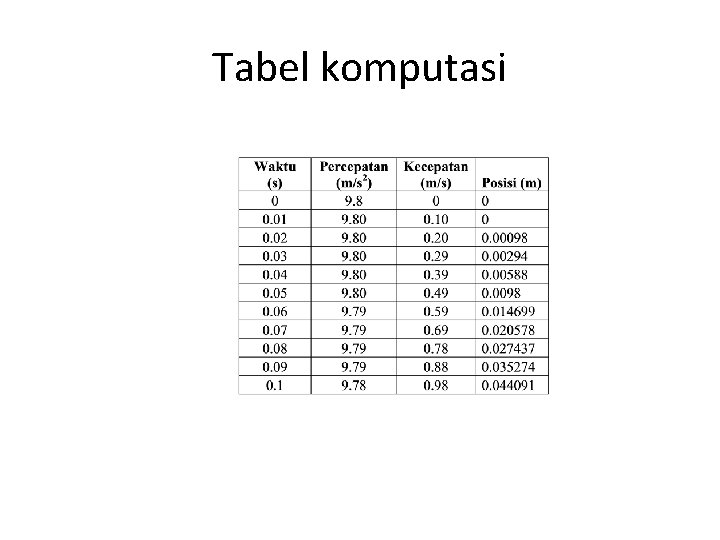
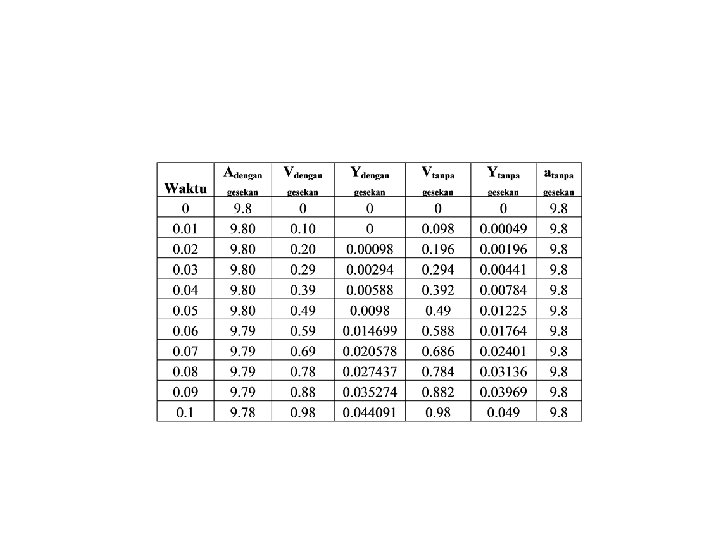
Tabel komputasi

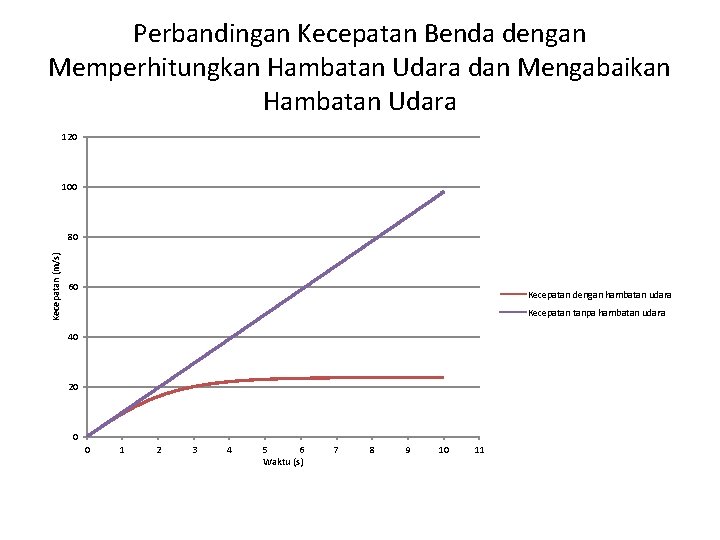
Perbandingan Kecepatan Benda dengan Memperhitungkan Hambatan Udara dan Mengabaikan Hambatan Udara 120 100 Kecepatan (m/s) 80 60 Kecepatan dengan hambatan udara Kecepatan tanpa hambatan udara 40 20 0 0 1 2 3 4 5 6 Waktu (s) 7 8 9 10 11

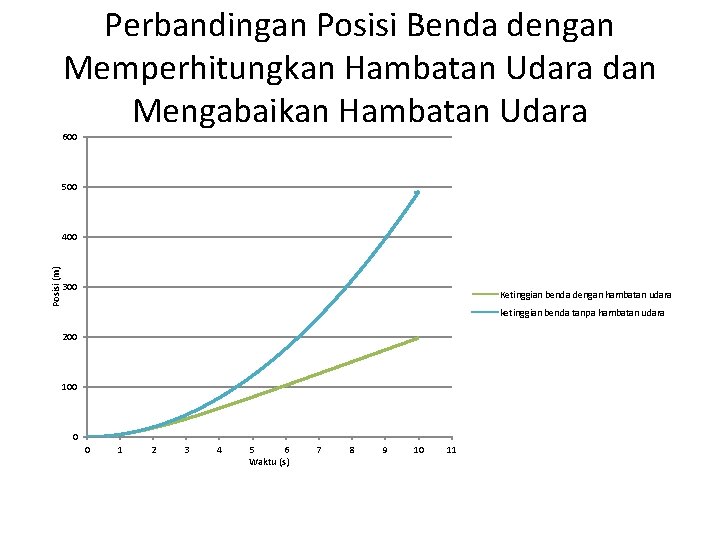
Perbandingan Posisi Benda dengan Memperhitungkan Hambatan Udara dan Mengabaikan Hambatan Udara 600 500 Posisi (m) 400 300 Ketinggian benda dengan hambatan udara ketinggian benda tanpa hambatan udara 200 100 0 0 1 2 3 4 5 6 Waktu (s) 7 8 9 10 11

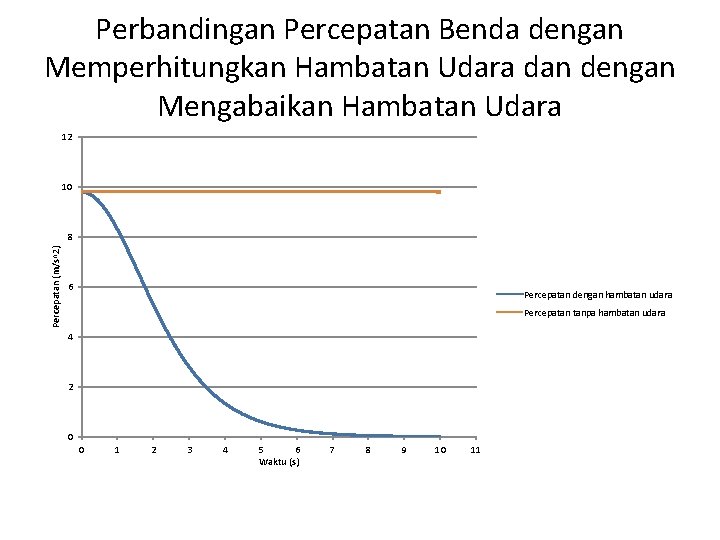
Perbandingan Percepatan Benda dengan Memperhitungkan Hambatan Udara dan dengan Mengabaikan Hambatan Udara 12 10 Percepatan (m/s^2) 8 6 Percepatan dengan hambatan udara Percepatan tanpa hambatan udara 4 2 0 0 1 2 3 4 5 6 Waktu (s) 7 8 9 10 11

Metode Euler-Cromer • Perhatikan persamaan berikut • seiring dengan bertambahnya waktu, kesalahan solusi numerik untuk posisi dan kecepatan semakin besar karena mengabaikan gradien lain disepanjang kurva y terhadap t.

Persamaan umum • Apabila menggunakan metode Euler, maka nilai v dan y sebelumnya dipakai untuk menghitung nilai v dan y yang baru. • dengan metode Euler-Cromer nilai v dan y sebelumnya dipakai untuk menghitung nilai y yang baru akan tetapi nilai y yang baru dipergunakan untuk menghitung nilai v yang baru.

• Contoh kasus nyata