METODE ENUMERASI IMPLISIT Pendahuluan Merupakan metode integer programming

Pendahuluan • Merupakan metode integer programming (IP) yang pada dasarnya hampir mirip dengan metode

Perbandingan Metode IP Branch and Bound Knapsack Enumerasi Implisit Variabel Keputusan = 2 Variabel

Prosedur Metode Enumerasi Implisit (1) 1. Melakukan penyempurnaan terbaik bagi suatu node : Input

Prosedur Metode Enumerasi Implisit (2) 2. Menguji fisibilitas dari semua fungsi pembatas Jenis Pembatas

Aturan pencabangan node • Jika langkah 1 didapatkan hasil fisible dan langkah 2 tidak

Node 1 Langkah 1 : Penyempurnaan terbaik : X 1 = 0 X 2

Node 1 Langkah 2 : Uji Fisibilitas Pembatas P 1 : X 1 =

Node 2 Langkah 1 : Penyempurnaan terbaik : X 1 = 0 X 2

Node 2 Langkah 2 : Uji Fisibilitas Pembatas P 1 : X 1 =

Node 3 Langkah 1 : Penyempurnaan terbaik : X 1 = 1 X 2

Node 3 Langkah 2 : Uji Fisibilitas Pembatas P 1 : X 1 =

Node 4 Langkah 1 : Penyempurnaan terbaik : X 1 = 1 X 2

Node 4 Langkah 2 : Uji Fisibilitas Pembatas P 1 : X 1 =

Node 6 Langkah 1 : Penyempurnaan terbaik : X 1 = 1 X 2

Node 6 Langkah 2 : Uji Fisibilitas Pembatas P 1 : X 1 =

Node 7 Langkah 1 : Penyempurnaan terbaik : X 1 = 1 X 2

Node 7 Langkah 2 : Uji Fisibilitas Pembatas P 1 : X 1 =

Node 7 • Merupakan calon solusi yang didapatkan • Masukkan nilai variabel keputusan pada

Node 5 Langkah 1 : Penyempurnaan terbaik : X 1 = 1 X 2

Node 5 Langkah 2 : Uji Fisibilitas Pembatas P 1 : X 1 =

Node 8 Langkah 1 : Penyempurnaan terbaik : X 1 = 1 X 2

Node 8 Langkah 2 : Uji Fisibilitas Pembatas P 1 : X 1 =

Node 9 Langkah 1 : Penyempurnaan terbaik : X 1 = 1 X 2

Node 9 Langkah 2 : Uji Fisibilitas Pembatas P 1 : X 1 =

Node 9 • Merupakan calon solusi yang didapatkan • Masukkan nilai variabel keputusan pada

Latihan soal : • Jenis Berat (kg) Harga (Rp) 1 1000 70 75. 000

Latihan soal : • Jenis mesin Berat/unit Volume/unit Harga/unit 1 5 1 4 2

Slides: 34

Download presentation

METODE ENUMERASI IMPLISIT

Pendahuluan • Merupakan metode integer programming (IP) yang pada dasarnya hampir mirip dengan metode knapsack. • Semua variabel keputusan harus berharga 0 atau 1

Perbandingan Metode IP Branch and Bound Knapsack Enumerasi Implisit Variabel Keputusan = 2 Variabel Keputusan ≥ 2 Fungsi Pembatas ≥ 1 Fungsi Pembatas = 1 Fungsi Pembatas ≥ 1 Nilai VK bernilai semua Nilai VK bernilai 0 atau 1 bilangan real dan memiliki arti sebenarnya

Prosedur Metode Enumerasi Implisit (1) 1. Melakukan penyempurnaan terbaik bagi suatu node : Input harga setiap variabel keputusan kepada fungsi pembatas untuk menentukan apakah fisible atau tidak

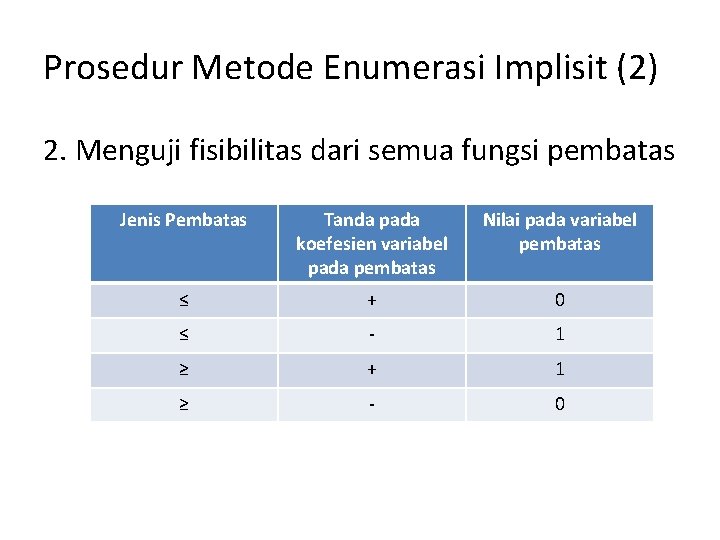
Prosedur Metode Enumerasi Implisit (2) 2. Menguji fisibilitas dari semua fungsi pembatas Jenis Pembatas Tanda pada koefesien variabel pada pembatas Nilai pada variabel pembatas ≤ + 0 ≤ - 1 ≥ + 1 ≥ - 0

Aturan pencabangan node • Jika langkah 1 didapatkan hasil fisible dan langkah 2 tidak fisible atau sebaliknya, maka lakukan pencabangan pada node tersebut • Jika langkah 1 dan 2 fisible, maka node berhenti (calon solusi) • Jika langkah 1 dan 2 tidak fisible, maka node berhenti (fathomed)

Contoh : Maks Z = -7 X 1 – 3 X 2 – 2 X 3 – X 4 – 2 X 5 s/t -4 X 1 – 2 X 2 + X 3 – 2 X 4 – X 5 ≤ -3 -4 X 1 – 2 X 2 - 4 X 3 + X 4 + 2 X 5 ≤ -7 Xi = 0 atau 1

Node 1 Langkah 1 : Penyempurnaan terbaik : X 1 = 0 X 2 = 0 X 3 = 0 X 4 = 0 X 5 = 0 P 1 : -4(0) – 2(0) + (0) – 2(0) – (0) ≤ -3 0 ≤ -3 (TF) P 2 : -4(0) – 2(0) – 4(0) + 2(0) ≤ -7 0 ≤ -7 (TF)

Node 1 Langkah 2 : Uji Fisibilitas Pembatas P 1 : X 1 = 1 X 2 = 1 X 3 = 0 X 4 = 1 X 5 = 1 -4(1) – 2(1) + (0) – 2(1) – (1) ≤ -3 -9 ≤ -3 (F) P 2 : X 1 = 1 X 2 = 1 X 3 = 1 X 4 = 0 X 5 = 0 -4(1) – 2(1) – 4(1) + (0) + 2(0) ≤ -7 -10 ≤ -7 (F)

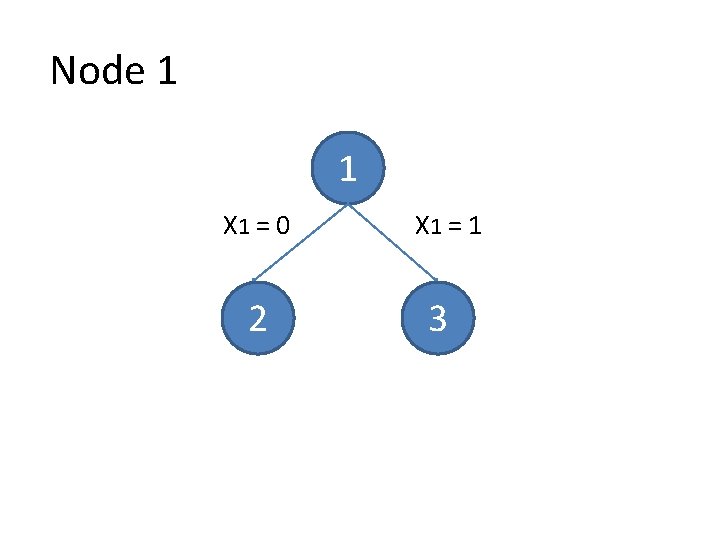
Node 1 1 X 1 = 0 2 X 1 = 1 3

Node 2 Langkah 1 : Penyempurnaan terbaik : X 1 = 0 X 2 = 0 X 3 = 0 X 4 = 0 X 5 = 0 P 1 : -4(0) – 2(0) + (0) – 2(0) – (0) ≤ -3 0 ≤ -3 (TF) P 2 : -4(0) – 2(0) – 4(0) + 2(0) ≤ -7 0 ≤ -7 (TF)

Node 2 Langkah 2 : Uji Fisibilitas Pembatas P 1 : X 1 = 0 X 2 = 1 X 3 = 0 X 4 = 1 X 5 = 1 -4(0) – 2(1) + (0) – 2(1) – (1) ≤ -3 -5 ≤ -3 (F) P 2 : X 1 = 0 X 2 = 1 X 3 = 1 X 4 = 0 X 5 = 0 -4(0) – 2(1) – 4(1) + (0) + 2(0) ≤ -7 -6 ≤ -7 (TF)

Node 3 Langkah 1 : Penyempurnaan terbaik : X 1 = 1 X 2 = 0 X 3 = 0 X 4 = 0 X 5 = 0 P 1 : -4(1) – 2(0) + (0) – 2(0) – (0) ≤ -3 -4 ≤ -3 (F) P 2 : -4(1) – 2(0) – 4(0) + 2(0) ≤ -7 -4 ≤ -7 (TF)

Node 3 Langkah 2 : Uji Fisibilitas Pembatas P 1 : X 1 = 1 X 2 = 1 X 3 = 0 X 4 = 1 X 5 = 1 -4(1) – 2(1) + (0) – 2(1) – (1) ≤ -3 -9 ≤ -3 (F) P 2 : X 1 = 1 X 2 = 1 X 3 = 1 X 4 = 0 X 5 = 0 -4(1) – 2(1) – 4(1) + (0) + 2(0) ≤ -7 -10 ≤ -7 (F)

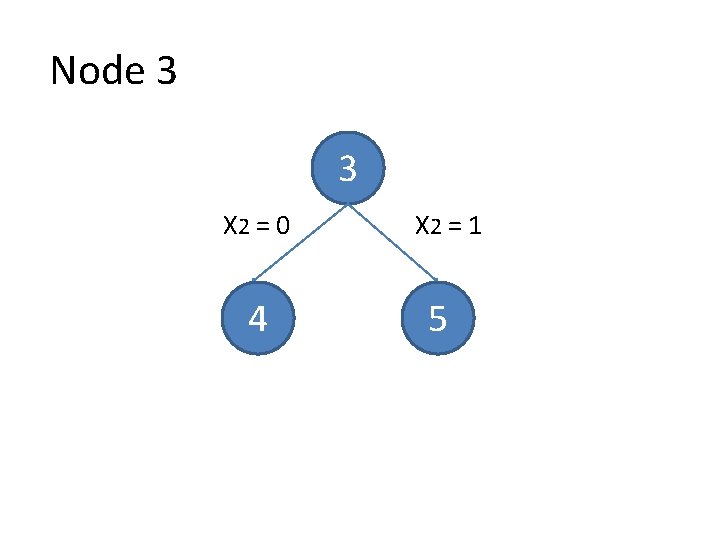
Node 3 3 X 2 = 0 4 X 2 = 1 5

Node 4 Langkah 1 : Penyempurnaan terbaik : X 1 = 1 X 2 = 0 X 3 = 0 X 4 = 0 X 5 = 0 P 1 : -4(1) – 2(0) + (0) – 2(0) – (0) ≤ -3 -4 ≤ -3 (F) P 2 : -4(1) – 2(0) – 4(0) + 2(0) ≤ -7 -4 ≤ -7 (TF)

Node 4 Langkah 2 : Uji Fisibilitas Pembatas P 1 : X 1 = 1 X 2 = 0 X 3 = 0 X 4 = 1 X 5 = 1 -4(1) – 2(0) + (0) – 2(1) – (1) ≤ -3 -7 ≤ -3 (F) P 2 : X 1 = 1 X 2 = 0 X 3 = 1 X 4 = 0 X 5 = 0 -4(1) – 2(0) – 4(1) + (0) + 2(0) ≤ -7 -8 ≤ -7 (F)

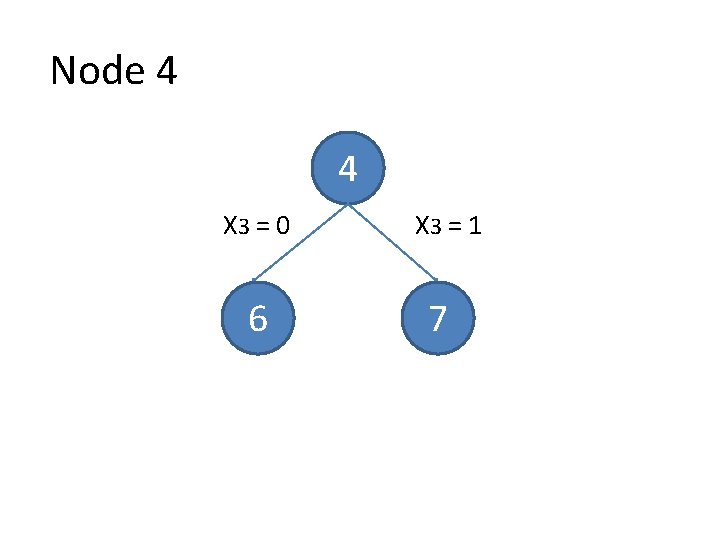
Node 4 4 X 3 = 0 6 X 3 = 1 7

Node 6 Langkah 1 : Penyempurnaan terbaik : X 1 = 1 X 2 = 0 X 3 = 0 X 4 = 0 X 5 = 0 P 1 : -4(1) – 2(0) + (0) – 2(0) – (0) ≤ -3 -4 ≤ -3 (F) P 2 : -4(1) – 2(0) – 4(0) + 2(0) ≤ -7 -4 ≤ -7 (TF)

Node 6 Langkah 2 : Uji Fisibilitas Pembatas P 1 : X 1 = 1 X 2 = 0 X 3 = 0 X 4 = 1 X 5 = 1 -4(1) – 2(0) + (0) – 2(1) – (1) ≤ -3 -7 ≤ -3 (F) P 2 : X 1 = 1 X 2 = 0 X 3 = 0 X 4 = 0 X 5 = 0 -4(1) – 2(0) – 4(0) + 2(0) ≤ -7 -4 ≤ -7 (TF)

Node 7 Langkah 1 : Penyempurnaan terbaik : X 1 = 1 X 2 = 0 X 3 = 1 X 4 = 0 X 5 = 0 P 1 : -4(1) – 2(0) + (1) – 2(0) – (0) ≤ -3 -3 ≤ -3 (F) P 2 : -4(1) – 2(0) – 4(1) + (0) + 2(0) ≤ -7 -10 ≤ -7 (F)

Node 7 Langkah 2 : Uji Fisibilitas Pembatas P 1 : X 1 = 1 X 2 = 0 X 3 = 1 X 4 = 1 X 5 = 1 -4(1) – 2(0) + (1) – 2(1) – (1) ≤ -3 -6 ≤ -3 (F) P 2 : X 1 = 1 X 2 = 0 X 3 = 1 X 4 = 0 X 5 = 0 -4(1) – 2(0) – 4(1) + (0) + 2(0) ≤ -7 -8 ≤ -7 (F)

Node 7 • Merupakan calon solusi yang didapatkan • Masukkan nilai variabel keputusan pada penyempurnaan terbaik X 1 = 1 X 2 = 0 X 3 = 1 X 4 = 0 X 5 = 0 Z = -7(1) – 3(0) – 2(1) – (0) – 2(0) = -9

Node 5 Langkah 1 : Penyempurnaan terbaik : X 1 = 1 X 2 = 1 X 3 = 0 X 4 = 0 X 5 = 0 P 1 : -4(1) – 2(1) + (0) – 2(0) – (0) ≤ -3 -6 ≤ -3 (F) P 2 : -4(1) – 2(1) – 4(0) + 2(0) ≤ -7 -6 ≤ -7 (TF)

Node 5 Langkah 2 : Uji Fisibilitas Pembatas P 1 : X 1 = 1 X 2 = 1 X 3 = 0 X 4 = 1 X 5 = 1 -4(1) – 2(1) + (0) – 2(1) – (1) ≤ -3 -9 ≤ -3 (F) P 2 : X 1 = 1 X 2 = 1 X 3 = 1 X 4 = 0 X 5 = 0 -4(1) – 2(1) – 4(1) + (0) + 2(0) ≤ -7 -10 ≤ -7 (F)

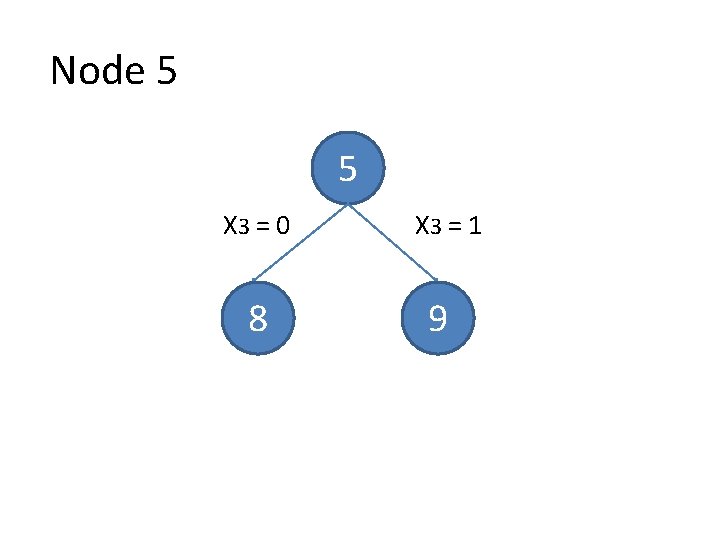
Node 5 5 X 3 = 0 8 X 3 = 1 9

Node 8 Langkah 1 : Penyempurnaan terbaik : X 1 = 1 X 2 = 1 X 3 = 0 X 4 = 0 X 5 = 0 P 1 : -4(1) – 2(1) + (0) – 2(0) – (0) ≤ -3 -6 ≤ -3 (F) P 2 : -4(1) – 2(1) – 4(0) + 2(0) ≤ -7 -6 ≤ -7 (TF)

Node 8 Langkah 2 : Uji Fisibilitas Pembatas P 1 : X 1 = 1 X 2 = 1 X 3 = 0 X 4 = 1 X 5 = 1 -4(1) – 2(1) + (0) – 2(1) – (1) ≤ -3 -9 ≤ -3 (F) P 2 : X 1 = 1 X 2 = 1 X 3 = 0 X 4 = 0 X 5 = 0 -4(1) – 2(1) – 4(0) + 2(0) ≤ -7 -6 ≤ -7 (TF)

Node 9 Langkah 1 : Penyempurnaan terbaik : X 1 = 1 X 2 = 1 X 3 = 1 X 4 = 0 X 5 = 0 P 1 : -4(1) – 2(1) + (1) – 2(0) – (0) ≤ -3 -5 ≤ -3 (F) P 2 : -4(1) – 2(1) – 4(1) + (0) + 2(0) ≤ -7 -10 ≤ -7 (F)

Node 9 Langkah 2 : Uji Fisibilitas Pembatas P 1 : X 1 = 1 X 2 = 1 X 3 = 1 X 4 = 1 X 5 = 1 -4(1) – 2(1) + (1) – 2(1) – (1) ≤ -3 -8 ≤ -3 (F) P 2 : X 1 = 1 X 2 = 1 X 3 = 1 X 4 = 0 X 5 = 0 -4(1) – 2(1) – 4(1) + (0) + 2(0) ≤ -7 -10 ≤ -7 (F)

Node 9 • Merupakan calon solusi yang didapatkan • Masukkan nilai variabel keputusan pada penyempurnaan terbaik X 1 = 1 X 2 = 1 X 3 = 1 X 4 = 0 X 5 = 0 Z = -7(1) – 3(1) – 2(1) – (0) – 2(0) = -12

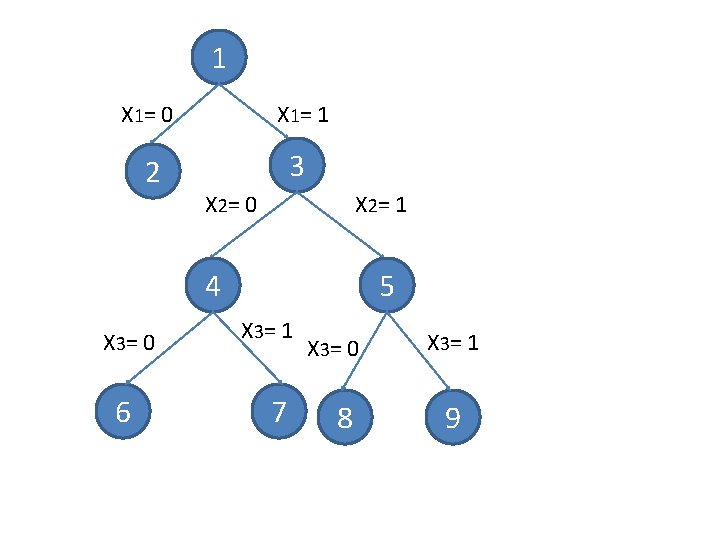
1 X 1= 0 X 1= 1 2 3 X 2= 0 X 2= 1 4 X 3= 0 6 5 X 3= 1 7 X 3= 0 8 X 3= 1 9

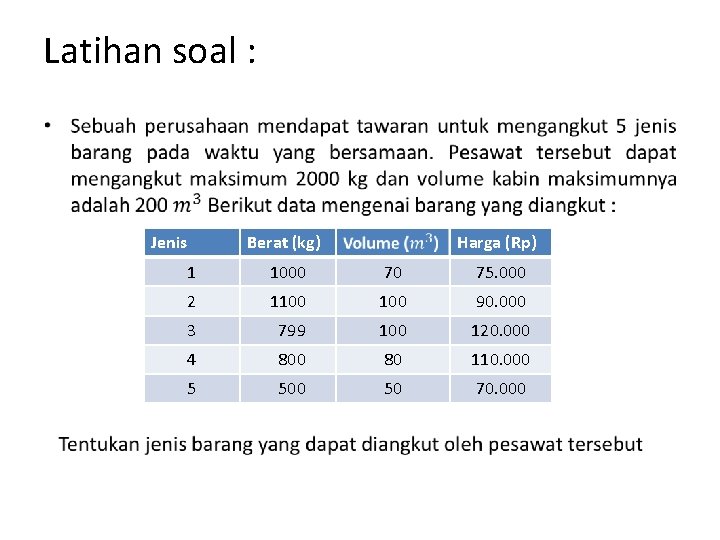
Latihan soal : • Jenis Berat (kg) Harga (Rp) 1 1000 70 75. 000 2 1100 90. 000 3 799 100 120. 000 4 800 80 110. 000 5 500 50 70. 000

Latihan soal : • Jenis mesin Berat/unit Volume/unit Harga/unit 1 5 1 4 2 8 8 7 3 3 6 6 4 2 5 5 5 7 4 4