METODE BAGI DUA 1 Interval yang didalamnya ada

METODE BAGI DUA 1. Interval yang didalamnya ada sebuah akar dibagi menjadi dua sub interval yang sama lebarnya. 2. Kemudian salah satu sub interval yang memuat akar dipilih sbg interval baru. 3. Ulangi langkah 1) dan 2) sampai didapatkan titik bagi/titik tengah xr sebuah interval dapat dianggap sbg 1/10/2022 Gunawan. ST. , MT - STMIK-BPN akar persamaan yang dicari.
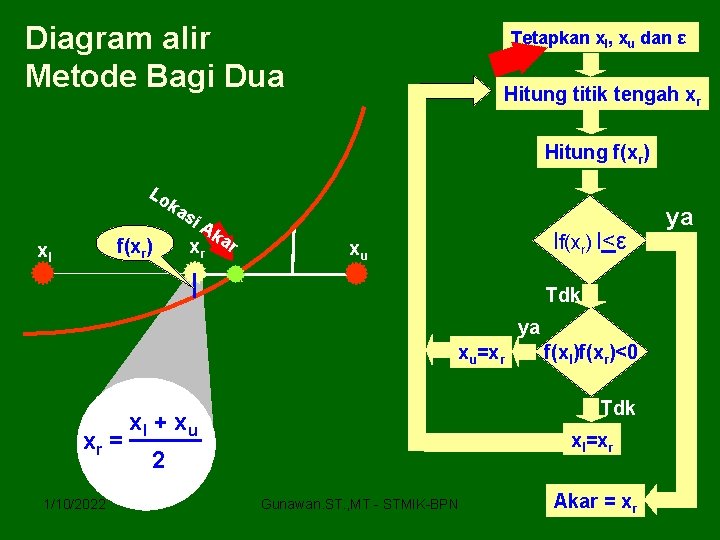
Diagram alir Metode Bagi Dua Tetapkan xl, xu dan ε Hitung titik tengah xr Hitung f(xr) Lo ka f(xr) xl si Ak xr ar lf(xr) l<ε xu Tdk f(xr) xr = 1/10/2022 ya xu=xr f(xl)f(xr)<0 Tdk xl + x u xl=xr 2 Gunawan. ST. , MT - STMIK-BPN Akar = xr ya

METODE POSISI SALAH Pers. Garis AB: y=f(x) B f(b) x 1 a f(a) b f(x 1) A 1/10/2022 x 3 Gunawan. ST. , MT - STMIK-BPN Lokasi Akar
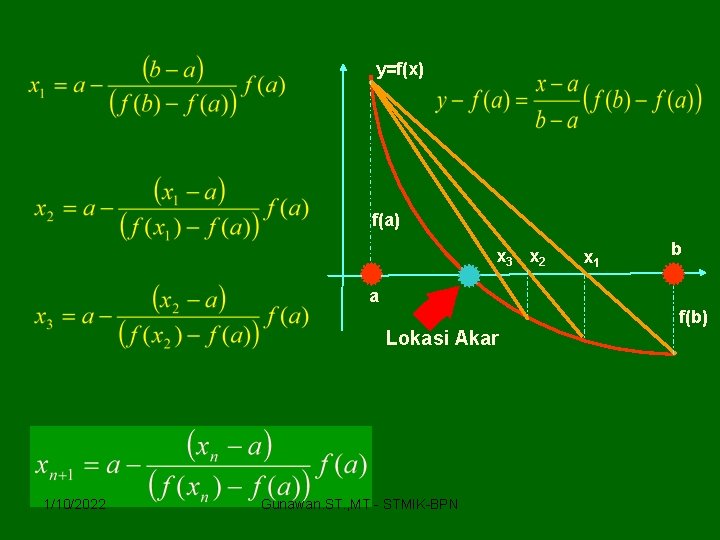
y=f(x) f(a) x 3 x 2 x 1 b a f(b) Lokasi Akar 1/10/2022 Gunawan. ST. , MT - STMIK-BPN

PROSEDUR PENYELESAIAN: 1. Tetapkan a dan b sedemikian hingga f(a) * f(b) < 0. 2. Hitung x 1: 3. Hitung f(x 1) 4. Jika f(a)*f(x 1) < 0: Jika f(a)*f(x 1) > 0: 1/10/2022 Gunawan. ST. , MT - STMIK-BPN

5. Hitung f(xn+1) 6. Jika Lanjutkan ke langkah 7, sebaliknya jika tidak maka kembali ke langkah 4 7. Akar persamaan adalah: x = xn+1 8. Selesai 1/10/2022 Gunawan. ST. , MT - STMIK-BPN

2 Cari akar persamaan 2 x + 5 - sin x = 0 Penyelesaian: f(x) = 2 x + 5 - sin x Ditetapkan a = -3, 5 dan b = -2, 5 sehingga f(a) = -2, 35078 dan f(b) = 0, 59847 Perhitungan pertama: 1/10/2022 Gunawan. ST. , MT - STMIK-BPN

Perhitungan kedua: 1/10/2022 Gunawan. ST. , MT - STMIK-BPN
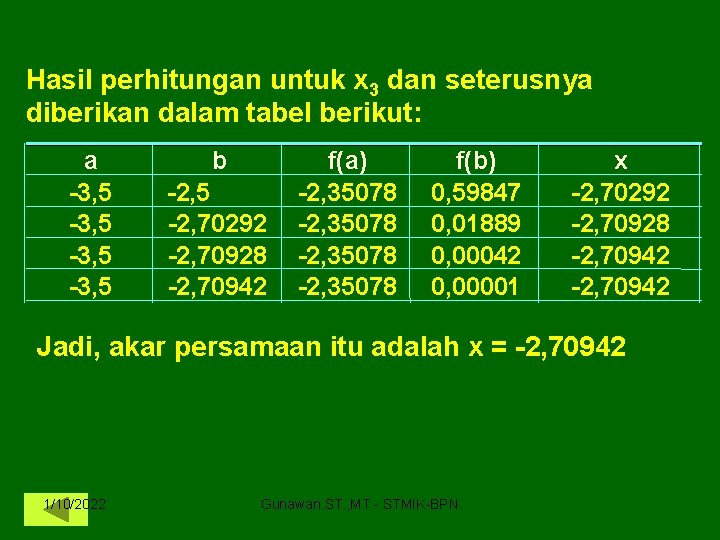
Hasil perhitungan untuk x 3 dan seterusnya diberikan dalam tabel berikut: a -3, 5 b -2, 5 -2, 70292 -2, 70928 -2, 70942 f(a) -2, 35078 f(b) 0, 59847 0, 01889 0, 00042 0, 00001 x -2, 70292 -2, 70928 -2, 70942 Jadi, akar persamaan itu adalah x = -2, 70942 1/10/2022 Gunawan. ST. , MT - STMIK-BPN
- Slides: 9