Metoda szeregu Fouriera Cel pracy Celem pracy jest

Metoda szeregu Fouriera

Cel pracy Celem pracy jest napisanie programu, który będzie wyznaczał przemieszczenia układu o jednym stopniu swobody z tłumieniem oraz wymuszeniem siłą okresową F(t). Położenie układu o jednym stopniu swobody można określić jednoznacznie za pomocą jednej współrzędnej uogólnionej. Rozpatrywany układ (rys. 1) składa się z nieodkształcalnej bryły, mogącej przemieszczać się prostoliniowym ruchem postępowym wzdłuż osi x połączonej z ostoją nieważką sprężyną oraz nieważkim tłumikiem. Rys. 1. Rozpatrywany układ o jednym stopniu swobody

Równanie ruchu Jeżeli na układ działa zmienne obciążenie w czasie w postaci siły F(t), to obciążenie takie nazywamy wymuszeniem siłowym. Równania ruchu można wyrazić następująco:

Metoda szeregu Fouriera (1) Występujące przy ruchu układów mechanicznych siły mają zazwyczaj charakter okresowy. Tylko w tym przypadku można stosować niżej opisaną metodę.

Metoda szeregu Fouriera (2) Niech siła będzie opisana funkcją czasu F(t), mającą okres τ. Funkcję tę można rozłożyć na składowe harmoniczne za pomocą szeregu Fouriera.

Metoda szeregu Fouriera (3) gdzie: j – dodatnia liczba całkowita, aj , bj – współczynniki nieskończonego szeregu. Każda składowa harmoniczna jest wyrazem szeregu Fouriera, na który rozkładamy badany przebieg. Każdy harmoniczny sygnał składa się ze składowej stałej (fizycznie oznacza wartość średnią) oraz ze składowych harmonicznych (fizycznie oznaczają przebiegi sinusoidalne sygnałów).

Metoda szeregu Fouriera (4) Równanie ruchu układu może być zapisane następująco:

Metoda szeregu Fouriera (5) Współczynniki rozkładu w szeregu Fouriera można wyrazić następująco:

Metoda szeregu Fouriera (6) Można wyznaczyć odpowiedź układu dla każdej składowej.

Metoda szeregu Fouriera (7) Odpowiedzi układu wyznaczone dla poszczególnych składowych.

Metoda szeregu Fouriera (8) Zgodnie z zasadą superpozycji, odpowiedzią wypadkową układu na okresową siłę wymuszającą jest suma odpowiedzi na każdą oddzielą składową harmoniczną wymuszenia.

Metoda szeregu Fouriera (9) Kompletna postać rozwiązania równowagi wygląda następująco:

Metoda szeregu Fouriera (10) gdzie: oraz

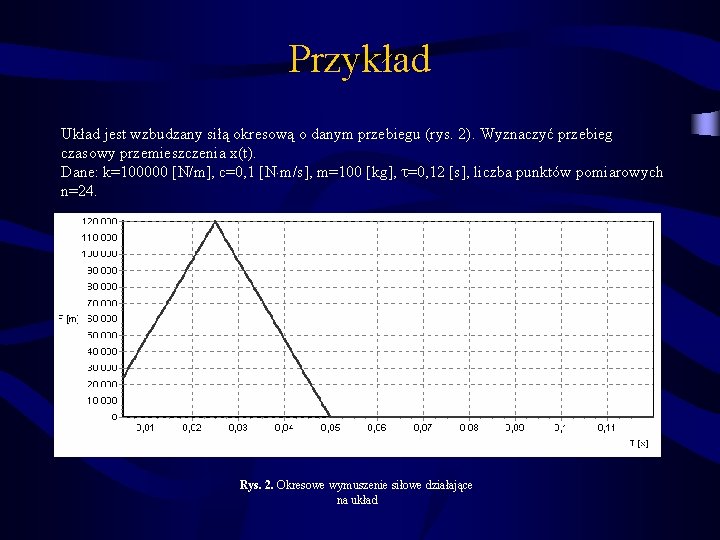
Przykład Układ jest wzbudzany siłą okresową o danym przebiegu (rys. 2). Wyznaczyć przebieg czasowy przemieszczenia x(t). Dane: k=100000 [N/m], c=0, 1 [N m/s], m=100 [kg], =0, 12 [s], liczba punktów pomiarowych n=24. Rys. 2. Okresowe wymuszenie siłowe działające na układ

Przykład (rozwiązanie) Rozwiązanie otrzymane za pomocą programu Math. CAD.

Wnioski Program Fourier wykonuje tzw. analizę harmoniczną czyli rozkłada wymuszenie okresowe w szereg Fouriera. Tak więc wymuszenie można przedstawić jako sumę wymuszeń harmonicznych, przy czym dokładność jest tym większa im więcej uwzględniamy składowych harmonicznych. W praktyce obliczeniowej uwzględnia się zwykle do kilkunastu składowych harmonicznych. Przy rozwiązywaniu przykładów wyniki obliczeń zmieniały się nieznacznie powyżej m=7.

Literatura [1] Giergiel J. : Drgania układów mechanicznych. Skrypt AGH, Kraków 1986 http: //victoria. bg. agh. edu. pl/BG/skrypty/ [2] Kruszewski J. Wittbrodt E. : Drgania układów mechanicznych w ujęciu komputerowym. WNT, Warszawa 1992 [3] Rao S. S. : Mechanical vibrations. Addison – Wesley Publishing Company, 1986