METODA PENENTUAN POSISI HORISONTAL METODA POLIGON Metoda Poligon

METODA PENENTUAN POSISI HORISONTAL

METODA POLIGON Metoda Poligon merupakan salah satu metoda penentuan posisi horisontal beberapa titik di lapangan dengan cara hitungan bertantai, dimana titik satu dengan titik lainnya dihubungkan secara berurutan dengan melakukan pengukuran sudut mendatar dan jarak mendatar sehingga membentuk suatu rangkaian titik-titik. Pengukuran poligon dilakukan untuk mendapatkan koordinat tititk-titik dilapangan, dengan tujuan agar dapat digunakan sebagai kerangka dasar pemetaan maupun untuk keperluan teknis.

Untuk mendapatkan koordinat titik-titik pada suatu poligon, dalam proses hitungannya menggunakan argumen sudut mendatar disetiap titik poligon dan jarak mendatar setiap sisi poligon. Selain itu diperlukan pula syarat agar dapta dilakukan hitungan koordinat, yaitu : Paling sedikit harus ada satu titik yang telah diketahui koordinatnya pada rangkaian poligon tersebut. Paling sedikit harus ada satu azimuth atau sudut jurusan sisi poligon yang telah diketahui.

POLIGON TERBUKA Pada poligon terbuka, proses hitungan koordinat titiknya dapat dibedakan menjadi 3 (tiga) jenis, yaitu: Poligon terbuka tidak terikat artinya jenis poligon terbuka ini tidak ada syarat geometris atau keterikatan geometris yang harus dipenuhi. Dalam hal ini, argumen sudut mendatar maupun jarak mendatar hasil ukuran dianggap benar, sehingga tidak perlu memberikan koreksi geometris terhadap data tersebut. Poligon ini ditandai dengan hanya diketahui 1 (satu) koordinat titik dan 1 (satu) azimuth / sudut jurusan pada sisi poligon. A.

b. Poligon terbuka terikat sempurna artinya jenis poligon terbuka ini dalam proses hitungannya ada syarat geometris yang harus dipenuhi atau ada keterikatan geometris. Dalam hal ini, baik sudut mendatar maupun jarak mendatar hasil ukuran poligon ada keterikatan geometris. Oleh karena itu, poligon ini ditandai dengan adanya 2 (dua) koordinat titik dan 2 (dua) azimuth / sudut jurusan di kedua titik ujung poligon yang telah diketahui nilainya atau didefinisikan benar.

Syarat geometris poligon terikat sempurna : Akhir - Awal = ( β ) – n. 180° X akhir – X awal = (d. sin ) Y akhir – Y awal = (d. cos ) Dalam hal ini : = Azimuth sisi poligon. β = jumlah sudut-sudut ukuran poligon. n = bilangan bulat positif atau angka kelipatan yang sesuai. X, Y = koordinat titik ujung poligon yang diketahui nilainya. (d. sin ) = jumlah dari perkalian antara jarak dan sin setiap sisi poligon. (d. cos ) = jumlah dari perkalian antara jarak dan cos setiap sisi poligon.

c. Poligon terbuka terikat sepihak/sebagian artinya jenis poligon terbuka ini ada syarat geometris yang harus dipenuhi atau ada ketertarikan geometris sebagian. Dalam hal ini, salah satu argumen sudut mendatar atau jarak mendatar hasil ukuran poligon ada keterikatan geometris. Oleh karena itu, jenis poligon ini dapat dibedakan menjadi 2 (dua) tipe, yaitu : Poligon terbuka terikat sudut. Poligon terbuka terikat jarak.

Poligon terbuka terikat sudut merupakan poligon yang secara geometris mempunyai keterikatan sudut dengan azimuth pada kedua titik ujung sebagai pengontrolnya, dan dalam proses hitungannya, sudut hasil ukuran harus memenuhi syarat geometris, sedangkan jarak ukuran dianggap benar. Poligon ini ditandai dengan adanya 1 (satu) koordinat titik dan 2 (dua) azimuth di kedua titik ujung poligon yang telah diketahui / didefinisikan nilainya. Syarat geometris : Akhir - Awal = ( β ) – n. 180° = Azimuth. β = jumlah sudut-sudut ukuran poligon. n = bilangan bulat positif atau angka kelipatan yang sesuai. Ø

ØPoligon terbuka terikat jarak merupakan poligon yang secara geometris mempunyai keterikatan jarak dengan koordinat titik ujung poligon sebagai pengontrolnya, dan dalam proses hitungannya, jarak hasil ukuran harus memenuhi syarat geometris, sedangkan sudut ukuran dianggap benar. Poligon ini ditandai dengan adanya 2 (dua) koordinat titik di kedua ujung poligon dan 1 (sati) azimuth atau sudut jurusan yang telah diketahui/didefinisikan benar nilainya. Syarat geometris : X akhir – X awal = (d. sin ) Y akhir – Y awal = (d. cos )

Dalam hal ini : X, Y =koordinattitikpoligonyangdiketahui di kedua ujungnya. (d. sin ) = jumlah dari perkalian antara jarak dan sin setiap sisi poligon (d. cos )= jumlah dari perkalian antara jarak dan cos setiap sisi poligon. Skets poligon :

POLIGON TERTUTUP Suatu jaringan poligon dikatakan sebagai poligon tertutup apabila posisi horisontal titik awal dan titik akhir poligon tersebut sama atai berhimpit. Dengan pernyataan tersebut, maka secara matematis konfigurasi poligon tertutup dapat ditandai sebagai berikut : Koordinat Awal = Koordinat Akhir Azimuth Awal = Azimuth Akhir

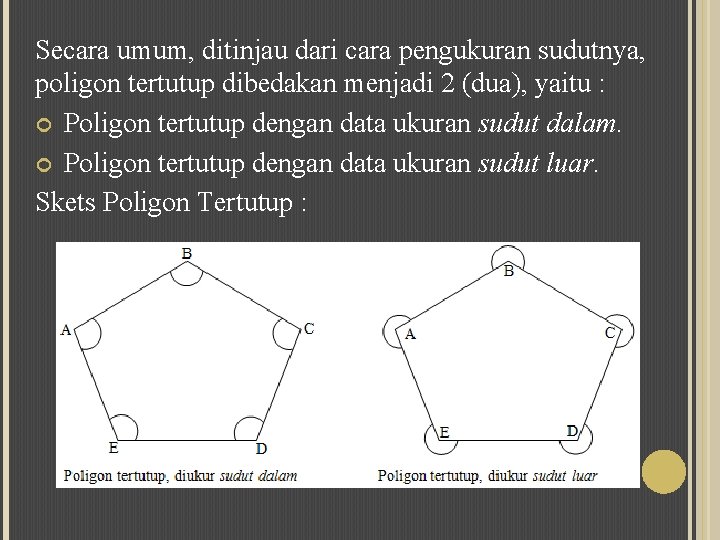
Secara umum, ditinjau dari cara pengukuran sudutnya, poligon tertutup dibedakan menjadi 2 (dua), yaitu : Poligon tertutup dengan data ukuran sudut dalam. Poligon tertutup dengan data ukuran sudut luar. Skets Poligon Tertutup :

Poligon tertutup merupakan poligon terikat sempurna, artinya baik sudut maupun jarak ukuran ada keterikatan geometris, sehingga dalam proses hitungannya data ukuran tersebut harus memenuhi syarat geometris. Syarat geometris poligon tertutup : ( β) – n. 180° = 0 (d. sin ) = 0 Dalam hal ini : ( β) = jumlah sudut-sudut ukuran pada poligon tertutup. n = bilangan bulat positif atau angka kelipatan yang sesuai. (d. sin ) = jumlah dari perkalian antara jarak ukuran dan sin . (d. cos )= jumlah dari perkalian antara jarak ukuran dan cos .

Perlu diketahui, dalam proses hitungan poligon tertutup bahwa : Untuk poligon tertutup dengan data ukuran sudut dalam, maka nilai n = N – 2 Untuk poligon tertutup dengan data ukuran sudut luar, maka nilai n = N + 2

Sistematika penyelesaian : 1. Perhatikan skets gambar poligon (sesuai data pengukuran lapangan). 2. Menghitung kesalahan total sudut ukuran atau clossing error polygon (fβ). 3. fβ = {( β ) – n. 180°} Menghitung nilai koreksi sudut dan nilai sudut terkoreksi. Nilai koreksi total = -fβ Besarnya koreksi setiap sudut ukuran (Δβ) = - fβ / N N = banyaknya sudut polygon yang diukur Nilai sudut terkoreksi : β = βu + Δβ

Menghitung azimuth setiap sisi poligon secara berurutan : BC = AB + β 2 - 180° CD = BC + β 3 - 180° = AB + β 2 + β 3 – ( 2 x 180° ) DE = CD + β 4 - 180° = AB + β 2 + β 3 + β 4 – ( 3 x 180° ) EA = DE + β 5 - 180° = AB + β 2 + β 3 + β 4 + β 5 – ( 4 x 180° ) Menghitung kesalahan total jarak ukuran dalam arah Absis (fx) dan arah Ordinat (fy) fx = { (d. sin )} fy = { (d. cos )}

6. Menghitung nilai koreksi jarak. Nilai koreksi jarak total arah X (absis) = - fx Besarnya koreksi setiap jarak ukuran dalam arah X : δx = (d / d). (-fx) Nilai koreksi jarak total arah Y (ordinat) = -fy Besarnya koreksi setiap jarak ukuran dalam arah Y : δy = (d / d). (-fy)

7. Menghitung koordinat titik B, C, D, dan E. XB = XA + d. AB sin AB + δx 1 XC = XB + d. BC sin BC + δx 2 XD = XC + d. CD sin CD + δx 3 XE = XD + d. DE sin DE + δx 4 YB = YA + d. AB cos AB + δy 1 YC = YB + d. BC cos BC + δy 2 YD = YC + d. CD cos CD + δy 3 YE = YD + d. DE cos DE + δy 4 ( Catatan : Koordinat titik A ini perlu dihitung dari titik E sebagai kontrol hitungan! )

PROSES DATA PRAKTIKUM DATA dan PROSESNYA DALAM FORMAT EXCEL. REFERENSI POLIGON TERTUTUP (LIHAT MODUL AJAR ILMU UKUR TANAH). SISTEMATIKA DAN TAHAPAN DIKETIK RAPI dengan koordinat awal : X= 150, 250 m ; Y = - 75, 125 m. BUATLAH PROGRAM EXCEL UNT PROSES DATA TSB. (hasilnya dicek dengan Calculator) HASIL AKHIR DITABELKAN DIGAMBAR DENGAN SKALA TERTENTU , format kertas HVS A 4. DIKUMPULKAN JUM’AT. SETIAP MHS HARUS PUNYA ARSIP.