METODA INTEGRASI GAUSS ILUSTRASI METODA TRAPESIUM ILUSTRASI METODA

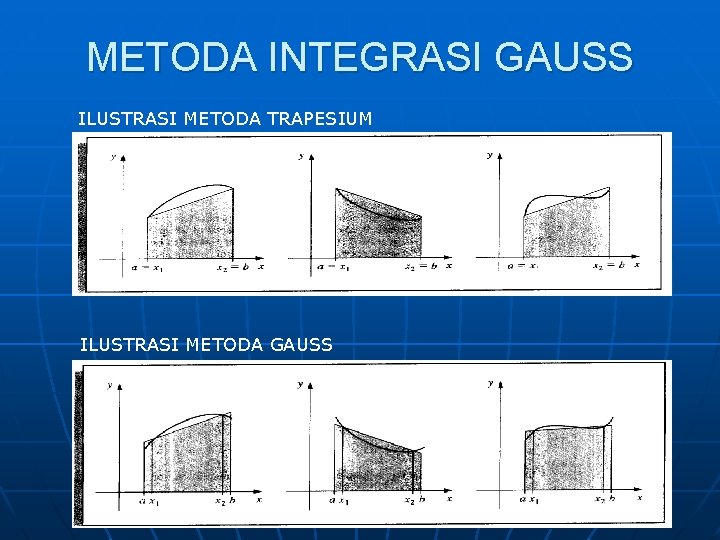
METODA INTEGRASI GAUSS ILUSTRASI METODA TRAPESIUM ILUSTRASI METODA GAUSS

Diperhatikan integral yang diaproksimasi oleh jumlahan berikut: Formula ini dikatakan mempunyai derajat akurasi p jika ia mampu memberikan hasil eksak jika f(x) polinomial berderajat paling tinggi p. Jadi, metoda midpoint derajat akurasi = 0. metoda trapesiaum derajat akurasi = 1. metoda Simpson derajat akurasi = 3. Metoda Gauss: menentukan koefisien c 1, c 2, . . . cn dan x 1, x 2, . . . xn sehingga formula memberikan akurasi 2 n-1. n = 2 derajat akurasi = 3. n = 3 derajat akurasi = 5.

Gauss Dasar, n = 2 n Akan ditentukan c 1, c 2, x 1, dan x 2 shg (*) memberikan hasil eksak bilamana f(x) polinomial berderajat 3 atau kurang, yaitu f(x)=1, f(x)=x 2 dan f(x)=x 3. Diperoleh sistem pers taklinier

Setelah diselesaikan diperoleh: Jadi bentuk dasar integrasi Gauss utk n =2 adalah: Transformasi variabel integrasi: x t = (2 x-a-b)/(b-a) menghasilkan:

CONTOH Hitunglah integral dengan metoda Gauss. Penyelesaian: a = 0, b = 4, f(x) = ex. Transformasi variabel, menghasilkan Badingkan dengan hasil eksak 53. 5982 dan metoda Simpson memberikan hasil 56. 7696. Gauss lebih akurat dari Simpson.

Menentukan koefisien dan akar untuk n besar 1. Membangun sistem persamaan taklinier dengan 2 n pers dan 2 n variabel melalui polinomial derajat sampai 2 n-1. 2. Akar polinomial Legendre sbg titik xi dan menghitung ci berdasarkan integral:

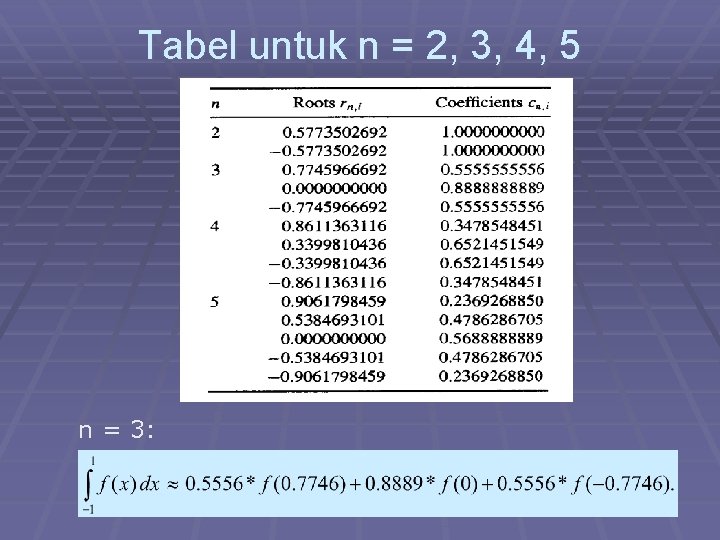
Tabel untuk n = 2, 3, 4, 5 n = 3:

LATIHAN § Diberikan masalah integral: a. Gunakan metoda integral Gauss n = 2, 3, 4 b. untuk mengaproksimasi integral ini. c. b. Periksalah error aproksimasing-masing n. d. Tentunya anda perlu menghitung hasil eksaknya. e. c. Bandingkan hasilnya dengan metoda Simpson. f. d. Terapkan metoda Gauss bersusun bila g. interval [0, π/4] dipecah menjadi 4 subinterval yg sama h. panjang.