Methods to Solve Quadratics Factoring Completing the Square







- Slides: 8

Methods to Solve Quadratics: Factoring, Completing the Square, or the Quadratic Formula and Equivalent Forms of Equations

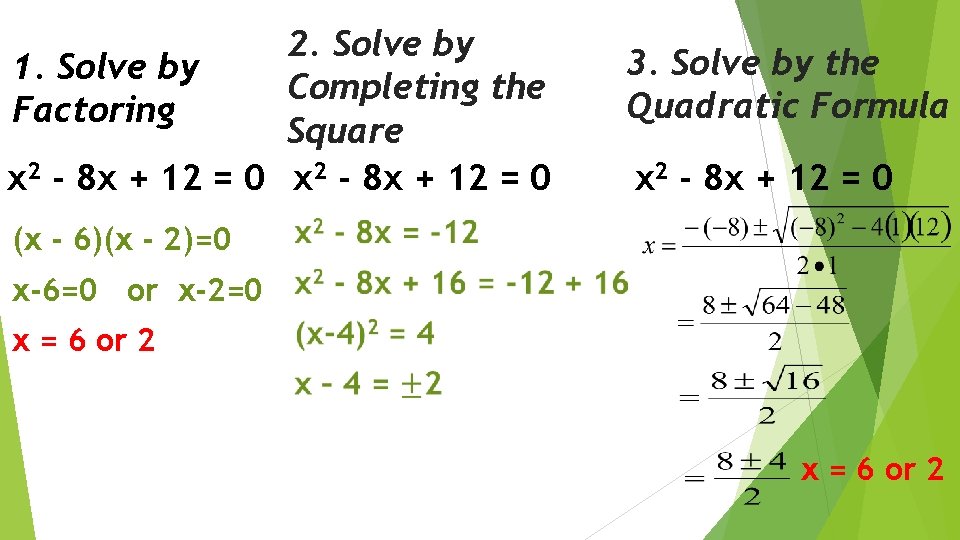
2. Solve by 1. Solve by Completing the Factoring Square x 2 - 8 x + 12 = 0 (x - 6)(x - 2)=0 3. Solve by the Quadratic Formula x 2 - 8 x + 12 = 0 x-6=0 or x-2=0 x = 6 or 2

When do you factor, complete the square, or use the quadratic formula to solve? When is factoring the most efficient method to use for solving a quadratic equation? When it’s not prime and fairly easy to find factors When factoring out the GCF or eliminating any fractional coefficients is possible. When is completing the square the most efficient method to use for solving a quadratic equation? When it is not possible (or it is very difficult) to factor the quadratic when the b and c value will be easy to deal with / not too many fractions When is the quadratic formula best? When it is not possible (or it is very difficult) to factor the quadratic If there are fraction coefficients

Solve these quadratic equations, using a different method for each: solve by factoring, solve by completing the square and solve by using the quadratic formula. Before starting, decide which method you will use on each one. 1. 2 x 2 + 5 x – 3 = 0 Factor to solve x = ½ or -3 (any method would have worked) 2. x 2 + 3 x – 5 = 0 Completing the square x= (or quad. formula would have worked) 3. ½x 2 - x – 4 = 0 Quadratic Formula x = 4 or -2 (any method would have worked) Any quadratic equation can be solved (if there is a solution) by the quadratic formula or completing the square – it’s your choice. Only some can be solved by factoring

You can write quadratic equations in many equivalent forms by using each solution method. Write / Match the equation to it’s equivalent forms 2 x 2 + 6 x = 36 2 x 2 + 6 x – 36 = 0 first put in standard form If using quadratic formula, it is equivalent to: 2 x 2 + 6 x – 36 = 0 If factored, it is equivalent to: 2(x 2 + 3 x – 18) = 0 Or 2(x + 6)(x – 3) = 0 Or roots: (-6, 0), (3, 0) x = -6, 3 x= -6, 3

You can write quadratic equations in many equivalent forms by using each solution method. Write / Match the equation to it’s equivalent forms x 2 – 6 x + 7 = 0 Can’t be factored If completing the square, it is equivalent to: x 2 – 6 x + 7 = 0 x 2 – 6 x = -7 x 2 – 6 x + 9 = -7 + 9 (x - 3)2 = 2 If using quadratic formula, it is equivalent to: x 2 - 6 x + 7 = 0

Match the equation to all equivalent equations in different forms. Select all choices that represent the same function/solution as what is given (x + 2 6) = 25 a. x 2 + 12 x – 25 = 0 d. (x + 11)(x + 1) b. e. x 2 + 12 x + 36 = 25 c. f.

Match the equation to all equivalent equations in different forms. Select all choices that represent the same function/solution as what is given 4 x 2 + 4 x – 6 = 3 a. 2(x - 3)(x + 1) = 0 b. c. d. f.