Methods of Proof correct complete A correct wellreasoned

증명의 중요성 Methods of Proof 수학에서 증명이란 • 수학적 문장의 진실성을 정밀하고 부정할 수 없도록 설명하는 정확(correct)하고 완전 (complete)한 기술이다. • A correct (well-reasoned, logically valid) and complete (clear, detailed) argument that rigorously and undeniably establishes the truth of a mathematical statement 증명에서의 기본적 사항 • 정확성: Correctness prevents us from fooling ourselves. • 완전성: Completeness allows anyone to verify the result. Page 2 Discrete Mathematics by Yang-Sae Moon

용어(Terminology) (1/3) Methods of Proof 정리(theorem) • 정리란 참(true)으로 밝혀진 명제이다. • A statement that has been proven to be true. 공리(axiom, postulates) • 증명된 정리 혹은 증명하고자 하는 정리의 가정/명제이다. (증명이 불필요한) • Assumptions (often unproven) defining the structures about which we are reasoning. (예: n이 짝수라면 n = 2 k라 나타낼 수 있다. ) 추론 규칙(rules of inference) • 논리적으로 유효한 주장(logically valid deductions)을 사용하여, 가정을 결론 으로 이끌어가는 증명의 과정이다. • Patterns of logically valid deductions from hypotheses to conclusions. Page 4 Discrete Mathematics by Yang-Sae Moon

용어(Terminology) (2/3) Methods of Proof 보조정리(lemma) • 다른 정리를 증명하는데 사용하는 간단한 정리이다. • A minor theorem used as a stepping-stone to proving a major theorem. “복잡한 내용이 정리이고, 간단한 내용이 보조정리”를 의미하는 것은 아님에 유의! 따름정리(corollary) • 어떤 정리가 증명되면, 이에 의하여 자연스럽게 증명되는 정리이다. • A minor theorem proved as an easy consequence of a major theorem. Page 5 Discrete Mathematics by Yang-Sae Moon

용어(Terminology) (3/3) Methods of Proof 가설(conjecture) • 증명되지는 않았지만 참으로 믿어지는 명제이다. • A statement whose truth values has not been proven. (A conjecture may be widely believed to be true, regardless. ) 이론(theory) • 주어진 공리(axiom)로부터 증명이 가능한 모든 정리(theorem)의 집합이다. • The set of all theorems that can be proven from a given set of axioms. Page 6 Discrete Mathematics by Yang-Sae Moon

추론 규칙 (Inference Rules) (2/2) Methods of Proof 각 추론 규칙은 “항진 명제인 함축(implication)”에 해당한다. ant. 1 ant. 2 … con. 에 해당하는 tautology는 “((ant. 1 ant. 2 … ) con. ”이다. Page 8 Discrete Mathematics by Yang-Sae Moon

추론 규칙 예제 (1/2) Methods of Proof 예제 • “It is below freezing now. Therefore, it is either below freezing or raining now. ”가 참인 것은 어떤 추론 규칙에 근거하는가? • 풀이 − p = “It is below freezing now. ”, q = “It is raining now. ” − 주어진 문장은 다음과 같은 추론 규칙에 근거하며, 이를 addition rule이라 한다. p p q Page 9 Discrete Mathematics by Yang-Sae Moon

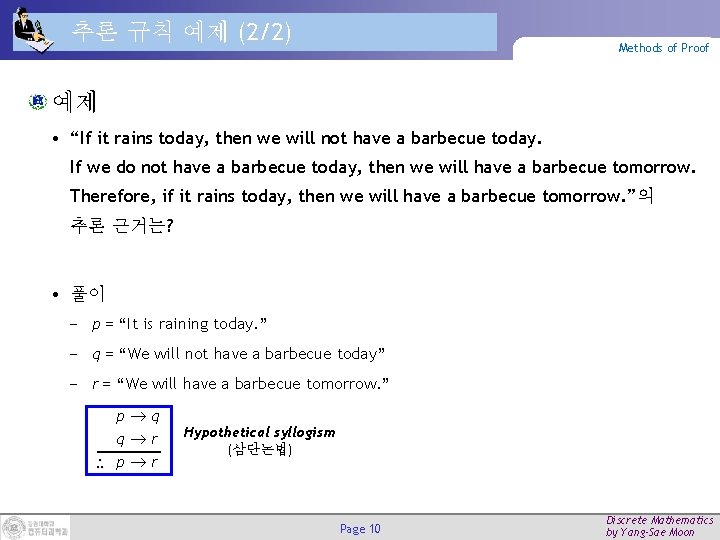
추론 규칙 예제 (2/2) Methods of Proof 예제 • “If it rains today, then we will not have a barbecue today. If we do not have a barbecue today, then we will have a barbecue tomorrow. Therefore, if it rains today, then we will have a barbecue tomorrow. ”의 추론 근거는? • 풀이 − p = “It is raining today. ” − q = “We will not have a barbecue today” − r = “We will have a barbecue tomorrow. ” p q q r p r Hypothetical syllogism (삼단논법) Page 10 Discrete Mathematics by Yang-Sae Moon

추론 규칙 종류 (1/2) Rule of inference Methods of Proof Tautology Name p p q p (p q) Addition p q p (p q) p Simplification p q ((p) (q)) (p q) Conjunction p p q q (p q)) q Modus ponens (긍정 논법) (the mode of affirming) (¬q (p q)) ¬p Modus tollens (부정 논법) (the mode of denying) ¬q p q ¬p p q가 true이면, 당연히 p와 q 모두 true이다. p가 true인 상태에서 p q가 true이면, 당연히 q는 true이다. Page 11 Discrete Mathematics by Yang-Sae Moon

추론 규칙 종류 (2/2) Rule of inference Methods of Proof Tautology Name p q q r p r ((p q) (q r)) (p r) Hypothetical syllogism (삼단 논법) p q ¬p q ((p q) ¬p) q Disjunctive syllogism p q ¬p r q r ((p q) (¬p r)) (q r) Resolution (분해) p가 false이고 p q이 true이면, 당연히 q는 true이다. Page 12 Discrete Mathematics by Yang-Sae Moon

Formal Proofs (1/2) Methods of Proof Formal Proof의 정의 • Formal proof란 주어진 가정(antecedent)에 기반하여 추론 규칙을 적용한 일 련의 단계(step)를 거쳐서 결론(consequent)을 도출하는 과정이다. − A formal proof of a conclusion C, given antecedents p 1, p 2, …, pn consists of a sequence of steps, each of which applies some inference rule to antecedents or to previously proven statements to yield a new true statement (the consequent). • 증명(proof)은 주어진 모든 가정이 true일 때 결론이 true임을 보이는 과정이다. − A proof demonstrates that if the antecedents are true, then the conclusion is true. Page 13 Discrete Mathematics by Yang-Sae Moon

Formal Proofs (2/2) Methods of Proof 예제 • 다음 가정이 “We will be home by sunset. ”이라는 결론을 도출함을 보여라. − “It is not sunny this afternoon and it is colder than yesterday. ” − “We will go swimming only if it is sunny. ” ( If we will go swimming, then it is sunny this …) − “If we do not go swimming, then we will take a canoe trip. ” − “If we take a canoe trip, then we will be home by sunset. ” • 풀이 − p = “It is sunny this afternoon. ” − q = “It is colder than yesterday. ” − r = “We will go swimming. ” − s = “We will take a canoe trip. ” − t = “We will be home by sunset. ” p p q q ¬q p q ¬p Modus ponens Modus tollens 단계 1 2 3 4 5 6 7 8 Page 14 과정 ¬p q ¬p r p ¬r ¬r s s s t t 이유 가정 단계 1의 simplification 가정 단계 2, 3 기반의 Modus tollens 가정 단계 4, 5 기반의 Modus ponens 가정 단계 6, 7 기반의 Modus ponens Discrete Mathematics by Yang-Sae Moon

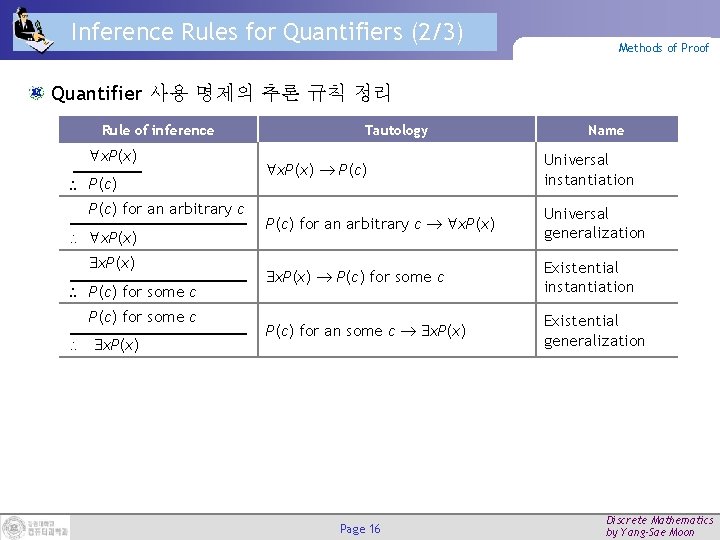
Inference Rules for Quantifiers (2/3) Methods of Proof Quantifier 사용 명제의 추론 규칙 정리 Rule of inference x. P(x) P(c) for an arbitrary c x. P(x) P(c) for some c x. P(x) Tautology Name x. P(x) P(c) Universal instantiation P(c) for an arbitrary c x. P(x) Universal generalization x. P(x) P(c) for some c Existential instantiation P(c) for an some c x. P(x) Existential generalization Page 16 Discrete Mathematics by Yang-Sae Moon

Inference Rules for Quantifiers (3/3) Methods of Proof 예제 • 다음 가정이 “Maria has taken a course in computer science. ”이라는 결론을 도출함을 보여라. − “Everyone in this discrete mathematics class has taken a course in computer science. ” − “Maria is a student in this class. ” • 풀이 − D(x) = “x is in this discrete mathematics class. ” − C(x) = “x has taken a course in computer science. ” − 가정: x(D(x) C(x)), D(Maria) − 결론: C(Maria) − 추론 과정 단계 1 2 3 4 과정 x(D(x) C(x)) D(Maria) C(Maria) D(Maria) C(Maria) 이유 가정 단계 1의 universal instantiation 가정 단계 2, 3 기반의 Modus ponens Page 17 Discrete Mathematics by Yang-Sae Moon

Summary of Proof Methods of Proof 함축(implication) p q의 증명을 위하여, 다음 방법들을 사용한다. • Direct proof: Assume p is true, and prove q. • Indirect proof: Assume ¬q, and prove ¬p. (대우의 증명에 해당) • Vacuous proof: Prove ¬p by itself. (가정이 false임을 증명) • Trivial proof: Prove q by itself. (결론이 항시 true임을 증명) • Proof by cases: To prove (p 1 p 2 . . pn) q, prove ((p 1 q) (p 2 q) . . (pn q)) Page 18 Discrete Mathematics by Yang-Sae Moon

Direct Proof (직접 증명) Methods of Proof Implication p q의 증명을 위하여, p가 true라 가정하고 여러 규칙과 기 존에 true로 증명된 정리를 사용하여 q가 true임을 증명한다. 예제 • Definition: An integer n is called odd iff n=2 k+1 for some integer k; n is even iff n=2 k for some k. • Axiom: Every integer is either odd or even. • Theorem: (For all numbers n) If n is an odd integer, then n 2 is an odd integer. • Proof: − If n is odd, then n = 2 k+1 for some integer k. − Thus, n 2 = (2 k+1)2 = 4 k 2 + 4 k + 1 = 2(2 k 2 + 2 k) + 1. − Therefore, n 2 is of the form 2 j + 1 (with j the integer 2 k 2 + 2 k), thus n 2 is odd. □ Page 19 Discrete Mathematics by Yang-Sae Moon

Indirect Proof (간접 증명) Methods of Proof Implication p q 대신 이의 대우인 ¬q ¬p를 증명한다. 예제 • Theorem: (For all integers n) If 3 n+2 is odd, then n is odd. • Proof: − Suppose that the conclusion is false, i. e. , n is even. − Then n=2 k for some integer k. − Then 3 n+2 = 3(2 k)+2 = 6 k+2 = 2(3 k+1). − Thus 3 n+2 is even, because it equals 2 j for integer j = 3 k+1. − So 3 n+2 is not odd. − We have shown that ¬(n is odd)→¬(3 n+2 is odd), thus its contra-positive (3 n+2 is odd) → (n is odd) is also true. □ Page 20 Discrete Mathematics by Yang-Sae Moon

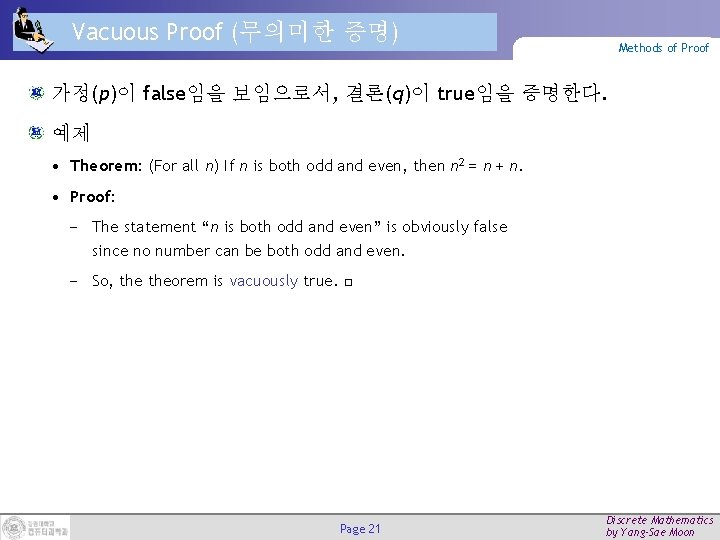
Vacuous Proof (무의미한 증명) Methods of Proof 가정(p)이 false임을 보임으로서, 결론(q)이 true임을 증명한다. 예제 • Theorem: (For all n) If n is both odd and even, then n 2 = n + n. • Proof: − The statement “n is both odd and even” is obviously false since no number can be both odd and even. − So, theorem is vacuously true. □ Page 21 Discrete Mathematics by Yang-Sae Moon

Trivial Proof (자명한 증명) Methods of Proof Implication p q에서, 결론(q)이 trivial하게 true임을 증명한다. 예제 • Theorem: (For integers n) If n is the sum of two prime numbers, then either n is odd or n is even. • Proof: − Any integer n is either odd or even. − So the conclusion of the implication is true regardless of the truth of the antecedent. − Thus the implication is true trivially. □ Page 22 Discrete Mathematics by Yang-Sae Moon

Proof by Cases (사례에 의한 증명) (2/2) Methods of Proof 예제 • Theorem: |xy| = |x||y|, where x and y are real numbers. (|x| = x if x 0, |x| = -x if x < 0) • Proof: − p = x and y are real numbers, q = |xy| = |x||y| − p = {x 0, y 0} {x 0, y < 0} {x < 0, y < 0} ▫ {x 0, y 0} q: |xy| = xy = |x||y| ▫ {x 0, y < 0} q: |xy| = -xy = x(-y) = |x||y| ▫ … − All the possible cases are proven to true, and thus, theorem is proven. □ Page 26 Discrete Mathematics by Yang-Sae Moon

Proof of Equivalence (동치 증명) Methods of Proof 상호조건 p ↔ q(“p if and only if q”)을 증명하기 위해서는 다음과 같은 tautology를 사용한다. (p ↔ q) ((p q) (q p)) • 즉, (p q)를 증명하고 (q p)를 증명함으로써, (p ↔ q)를 증명한다. Page 27 Discrete Mathematics by Yang-Sae Moon

Existence Proof (존재 증명) (1/2) Methods of Proof 증명하고자 하는 문장에 x. P(x) 형태의 quantifier/predicate가 포함된 경 우를 존재 증명(existence proof)이라 한다. If the proof of a statement of the form x. P(x) is called an existence proof. Page 28 Discrete Mathematics by Yang-Sae Moon

Existence Proof (존재 증명) (2/2) Methods of Proof 예제 • Theorem: There exists a positive integer n that is the sum of two perfect cubes in two different ways. (두 수의 세제곱의 합을 두 가지 방법으로 나타낼 수 있는 정수가 존재한다. ) (In other words, there exists a positive integer n such that n = j 3 + k 3 = l 3 + m 3, where j, k, l, and m are positive integers, and {j, k} {l, m}. ) • Proof: Consider n = 1729, j = 9, k = 10, l = 1, m = 12. Now just check that the equalities hold. □ Page 29 Discrete Mathematics by Yang-Sae Moon

Mistakes in Proofs Methods of Proof 예제 (mistakes in proof) • Theorem: Prove 1 = 2. • Proof: − Let a and b be the same positive integers. − a=b [주어진 정의] − a 2 = ab [양변에 a를 곱함] − a 2 - b 2 = ab - b 2 [양변에서 b 2를 뺌] − (a – b)(a + b) = b(a – b) [인수분해] − a+b=b [양변을 (a-b)로 나눔] − 2 b = b [since a = b] − 2 = 1. [양변을 b로 나눔] What is wrong? (a – b) is zero since a = b, and thus, we cannot use (a – b) as a divisor. Page 31 Discrete Mathematics by Yang-Sae Moon

Homework #1 Methods of Proof Page 32 Discrete Mathematics by Yang-Sae Moon