Methods of Motion Mathy AP Physics C Displacement

Methods of Motion Mathy AP Physics C

Displacement vs Distance! Displacement (x or y) "Change in position" It is not necessarily the total distance traveled. In fact, displacement and distance are entirely different concepts. Displacement is relative to an axis. o o o "x" displacement means you are moving horizontally either right or left. "y" displacement means you are moving vertically either up or down. The word change is expressed using the Greek letter DELTA ( Δ ). To find the change you ALWAYS subtract your FINAL - INITIAL position The expressions can be generic or specific Distance - How far you travel regardless of direction.

15 parsecs = 48. 9 light years Compare Han Solo’s Displacement vs distance

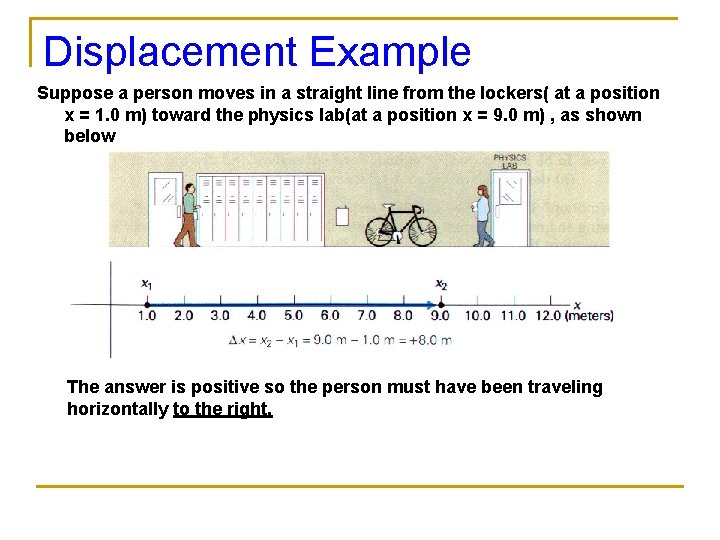
Displacement Example Suppose a person moves in a straight line from the lockers( at a position x = 1. 0 m) toward the physics lab(at a position x = 9. 0 m) , as shown below The answer is positive so the person must have been traveling horizontally to the right.

Displacement Example 2 Suppose the person turns around! The answer is negative so the person must have been traveling horizontally to the left What is the DISPLACEMENT for the entire trip? What is the total DISTANCE for the entire trip?

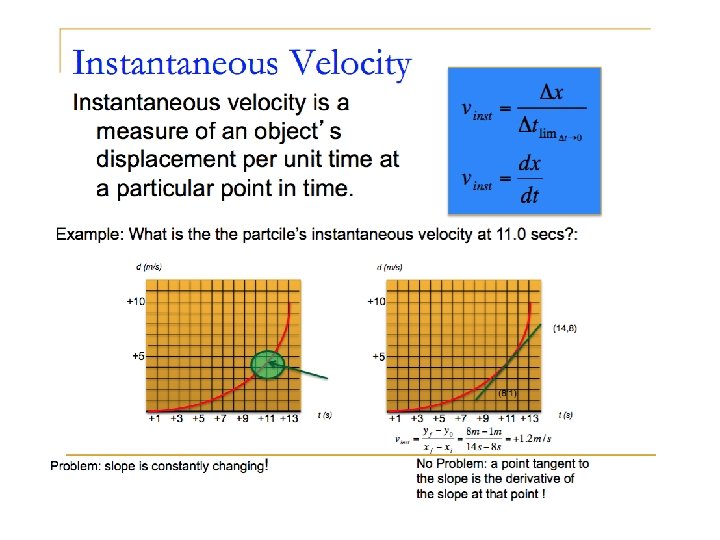
I & II Average Velocity Methods Velocity is defined as: “The RATE at which DISPLACEMENT changes”. Rate = ANY quantity divided by TIME. Average SPEED is simply the “RATE at which DISTANCE changes”. Units: m/s ft/s km/ hr cm/yr * 1 m/s= 2. 24 mi/hr

Slope – A basic graph model Read Only A basic model for understanding graphs in physics is SLOPE. Using the model - Look at the formula for velocity. Who gets to play the role of the slope? Velocity Who gets to play the role of the y-axis or the rise? Displacement Who get to play the role of the x-axis or the run? Time What does all the mean? It means that if your are given a Displacement vs. Time graph, to find the velocity of an object during specific time intervals simply find the slope.

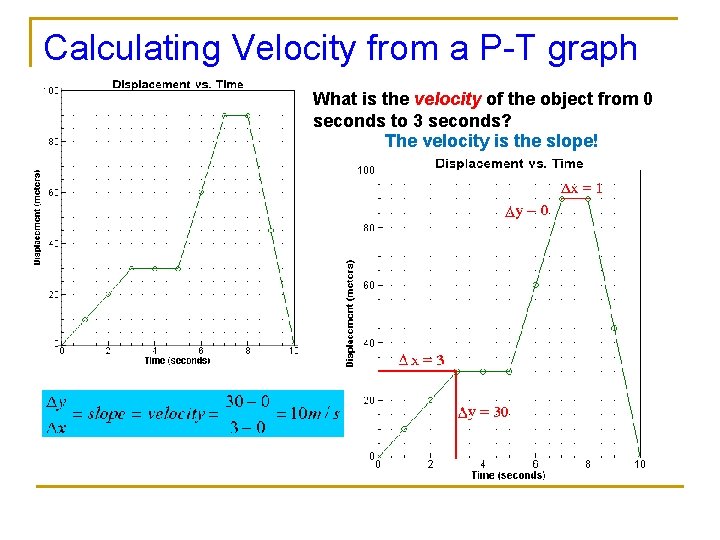
Calculating Velocity from a P-T graph What is the velocity of the object from 0 seconds to 3 seconds? The velocity is the slope!

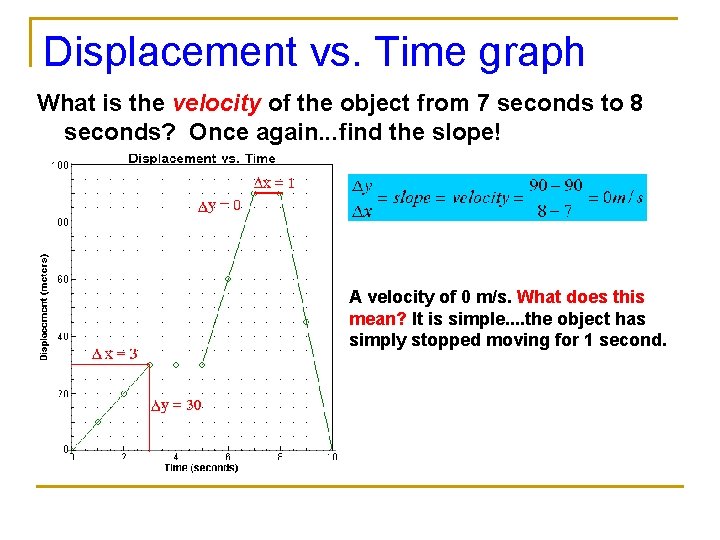
Displacement vs. Time graph What is the velocity of the object from 7 seconds to 8 seconds? Once again. . . find the slope! A velocity of 0 m/s. What does this mean? It is simple. . the object has simply stopped moving for 1 second.

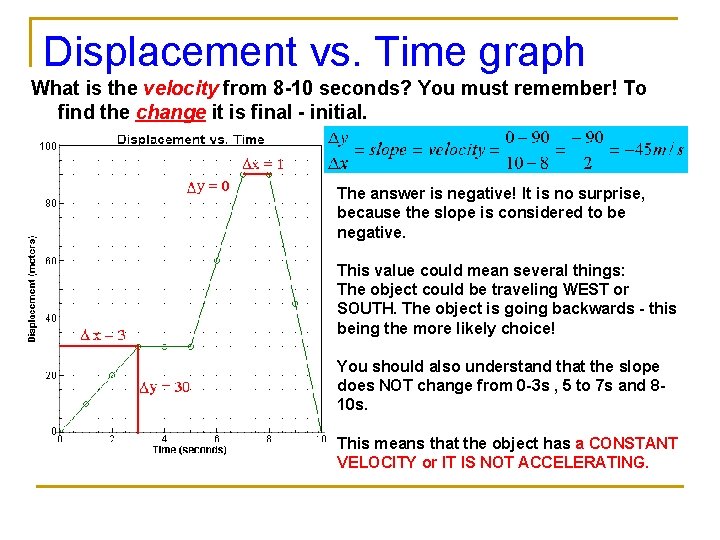
Displacement vs. Time graph What is the velocity from 8 -10 seconds? You must remember! To find the change it is final - initial. The answer is negative! It is no surprise, because the slope is considered to be negative. This value could mean several things: The object could be traveling WEST or SOUTH. The object is going backwards - this being the more likely choice! You should also understand that the slope does NOT change from 0 -3 s , 5 to 7 s and 810 s. This means that the object has a CONSTANT VELOCITY or IT IS NOT ACCELERATING.

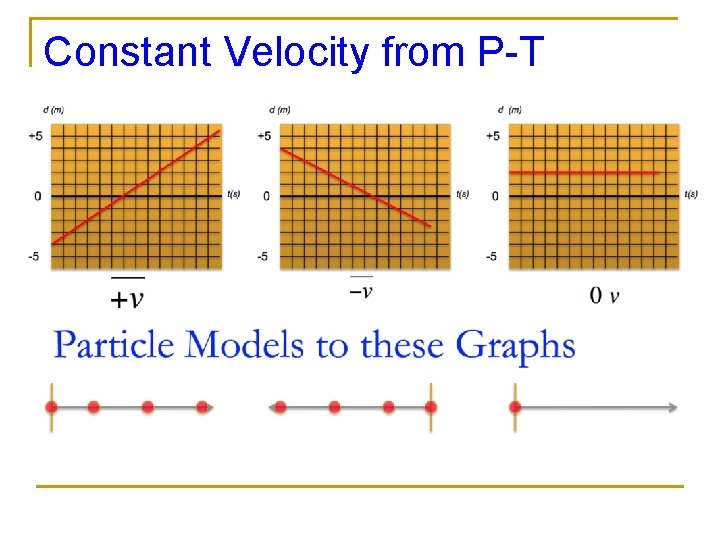
Constant Velocity from P-T Graphs

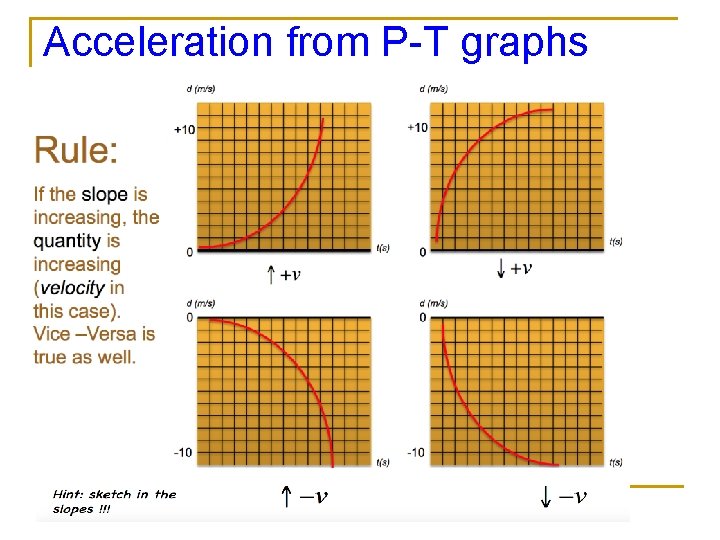
Acceleration from P-T graphs

Example Read Only A quarterback throws a pass to a defender on the other team who intercepts the football. Assume the defender had to run 50 m away from the quarterback to catch the ball, then 15 m towards the quarterback before he is tackled. The entire play took 8 seconds. Let's look at the defender's average velocity: Let's look at the defender's speed: “m/s” is the derived unit for both speed and velocity.

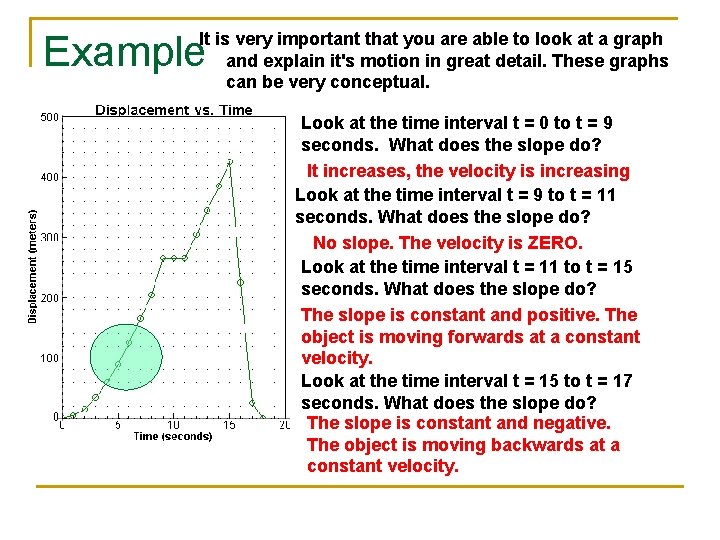
Example It is very important that you are able to look at a graph and explain it's motion in great detail. These graphs can be very conceptual. Look at the time interval t = 0 to t = 9 seconds. What does the slope do? It increases, the velocity is increasing Look at the time interval t = 9 to t = 11 seconds. What does the slope do? No slope. The velocity is ZERO. Look at the time interval t = 11 to t = 15 seconds. What does the slope do? The slope is constant and positive. The object is moving forwards at a constant velocity. Look at the time interval t = 15 to t = 17 seconds. What does the slope do? The slope is constant and negative. The object is moving backwards at a constant velocity.

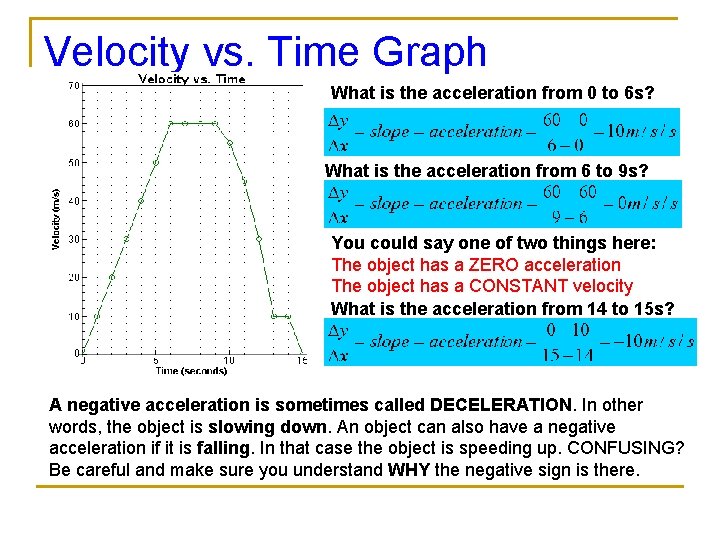
Velocity vs. Time Graph What is the acceleration from 0 to 6 s? What is the acceleration from 6 to 9 s? You could say one of two things here: The object has a ZERO acceleration The object has a CONSTANT velocity What is the acceleration from 14 to 15 s? A negative acceleration is sometimes called DECELERATION. In other words, the object is slowing down. An object can also have a negative acceleration if it is falling. In that case the object is speeding up. CONFUSING? Be careful and make sure you understand WHY the negative sign is there.

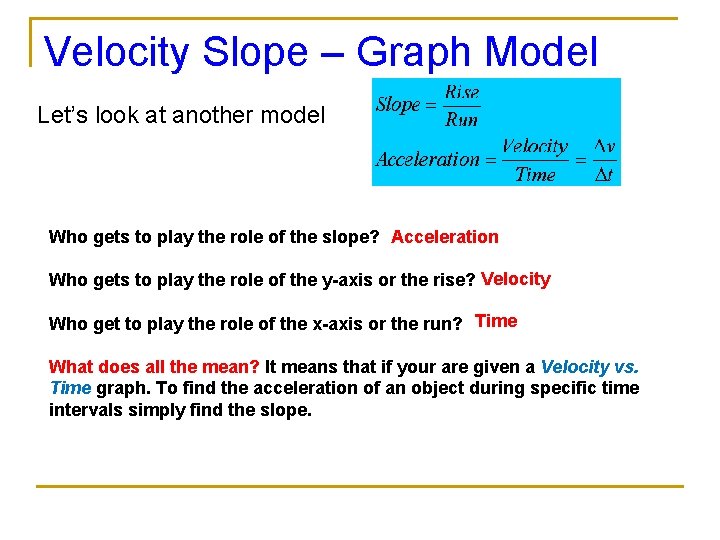
Velocity Slope – Graph Model Let’s look at another model Who gets to play the role of the slope? Acceleration Who gets to play the role of the y-axis or the rise? Velocity Who get to play the role of the x-axis or the run? Time What does all the mean? It means that if your are given a Velocity vs. Time graph. To find the acceleration of an object during specific time intervals simply find the slope.

III. 2. 6 (cont. ) Average Acceleration is the RATE at which VELOCITY changes. A truck accelerates from 10 m/s to 30 m/s in 2. 0 seconds. What is the acceleration? Suppose the same truck then slows down to 5 m/s in 4 seconds. What is the acceleration? “m/s/s” or “m/s 2” is the derived unit for acceleration.

Beware – the signs can confuse! Suppose a ball is thrown straight upwards at 40 m/s. It takes 4 seconds to reach its maximum height, then another 4 seconds back down to the point where it was thrown. Assume it is caught with the same speed it was thrown. Calculate the acceleration upwards and downwards. This negative sign came from using the DELTA This negative sign came from the DIRECTION of the velocity. It is no surprise you get a negative answer both ways as gravity acts DOWNWARDS no matter if the ball goes up or down. It is GRAVITY which changes the ball’s velocity.

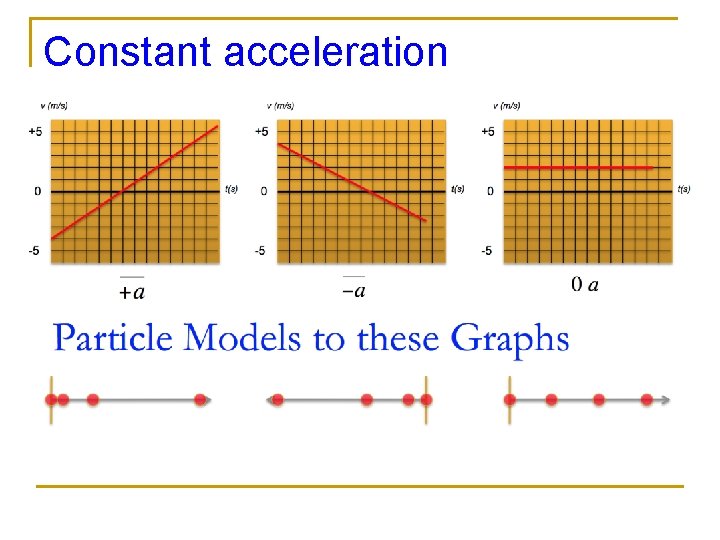
Constant acceleration

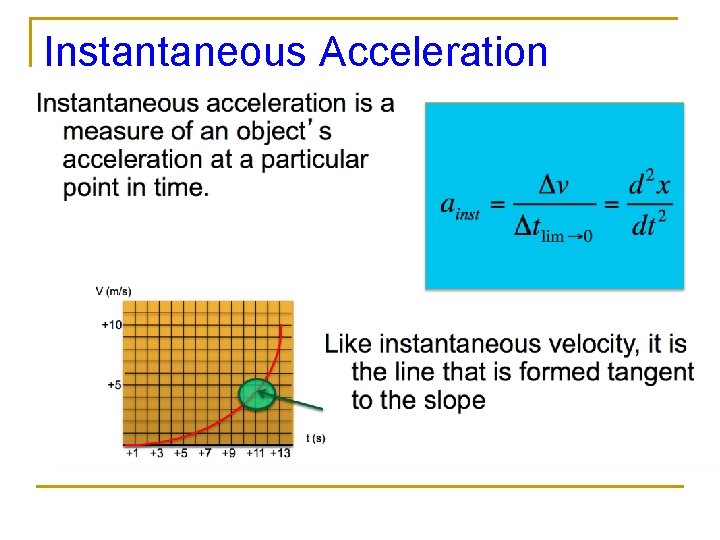
Instantaneous Acceleration

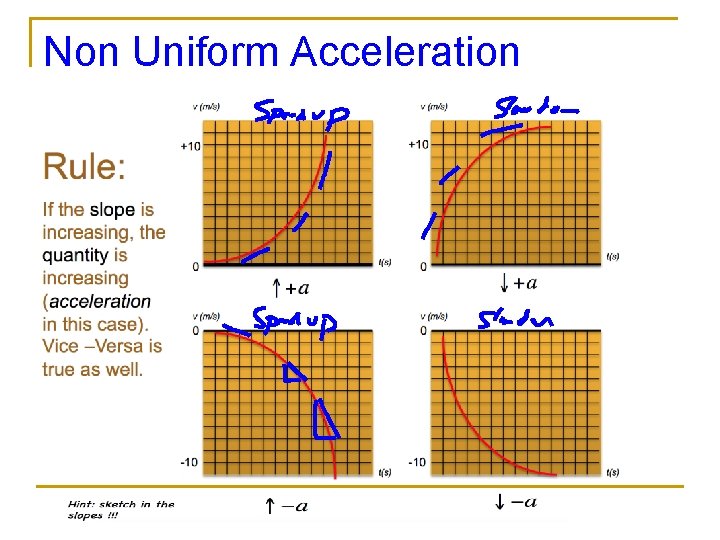
Non Uniform Acceleration

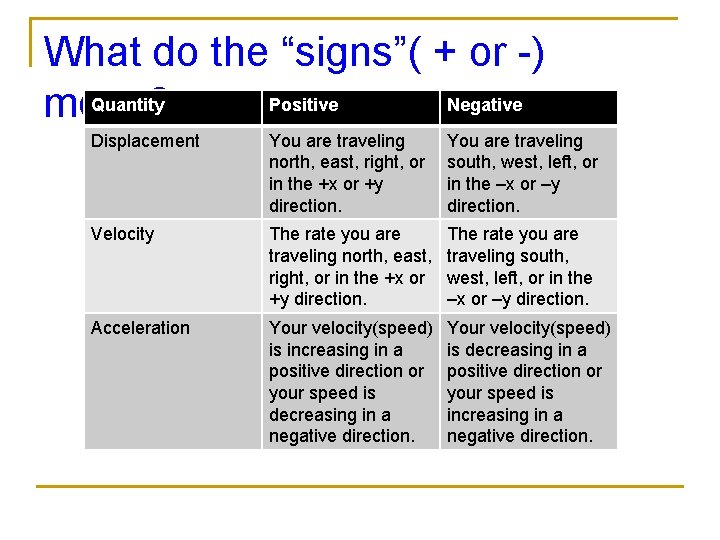
What do the “signs”( + or -) Quantity Positive Negative mean? Displacement You are traveling north, east, right, or in the +x or +y direction. You are traveling south, west, left, or in the –x or –y direction. Velocity The rate you are traveling north, east, right, or in the +x or +y direction. The rate you are traveling south, west, left, or in the –x or –y direction. Acceleration Your velocity(speed) is increasing in a positive direction or your speed is decreasing in a negative direction. Your velocity(speed) is decreasing in a positive direction or your speed is increasing in a negative direction.

Area – the “other” basic graph Another basic model for understanding graphs in model physics is AREA. Let's try to algebraically make our formulas look like the one above. We'll start with our formula for velocity. Who gets to play the role of the base? Time Who gets to play the role of the height? Velocity What kind of graph is this? A Velocity vs. Time graph ( velocity = yaxis & time = x-axis) Who gets to play the role of the Area? Displacement

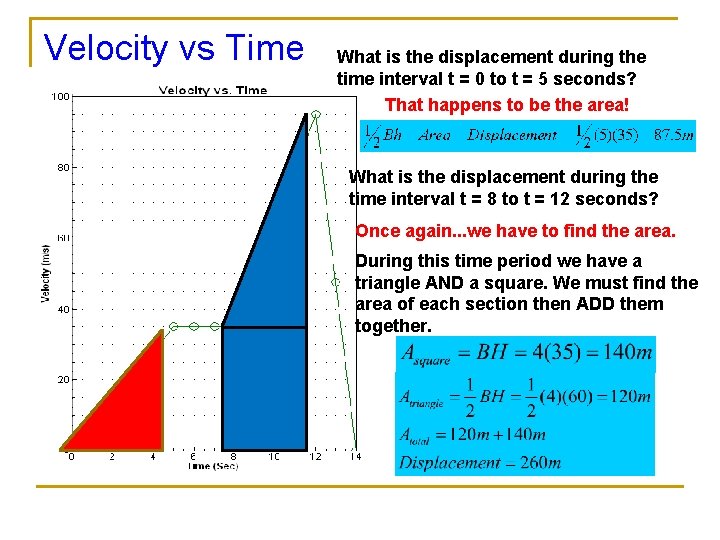
Velocity vs Time What is the displacement during the time interval t = 0 to t = 5 seconds? That happens to be the area! What is the displacement during the time interval t = 8 to t = 12 seconds? Once again. . . we have to find the area. During this time period we have a triangle AND a square. We must find the area of each section then ADD them together.

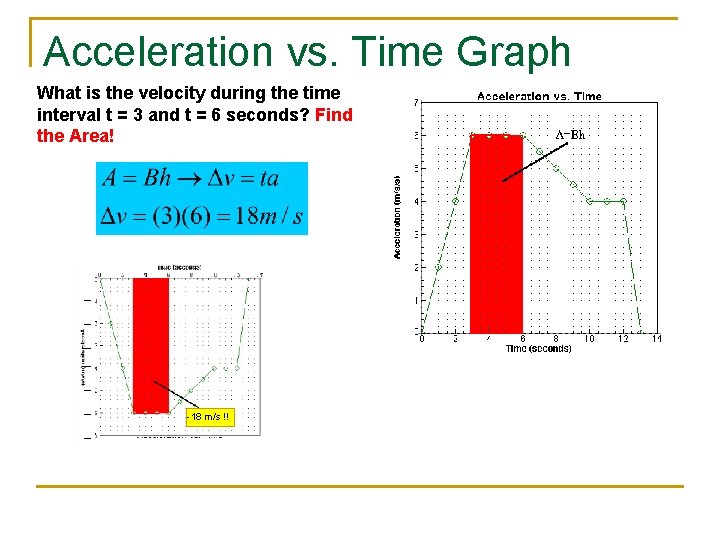
Acceleration vs. Time Graph What is the velocity during the time interval t = 3 and t = 6 seconds? Find the Area! -18 m/s !!

IV. Displacement as a function of time 2

V. Displacement as a function of velocity

The Big 5 Kinematic Equations

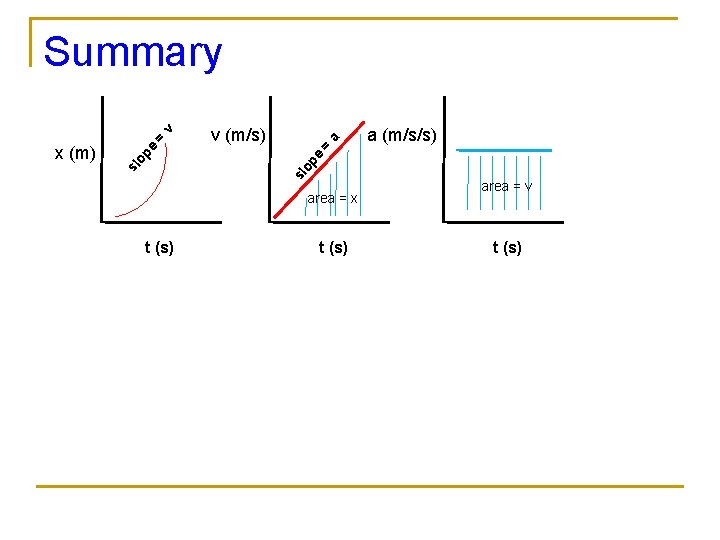
Summary There are 3 types of MOTION graphs n Displacement(position) vs. Time n Velocity vs. Time n Acceleration vs. Time There are 2 basic graph models n Slope n Area

sl area = x t (s) a (m/s/s) = a v (m/s) op e sl x (m) = v Summary t (s) area = v t (s)

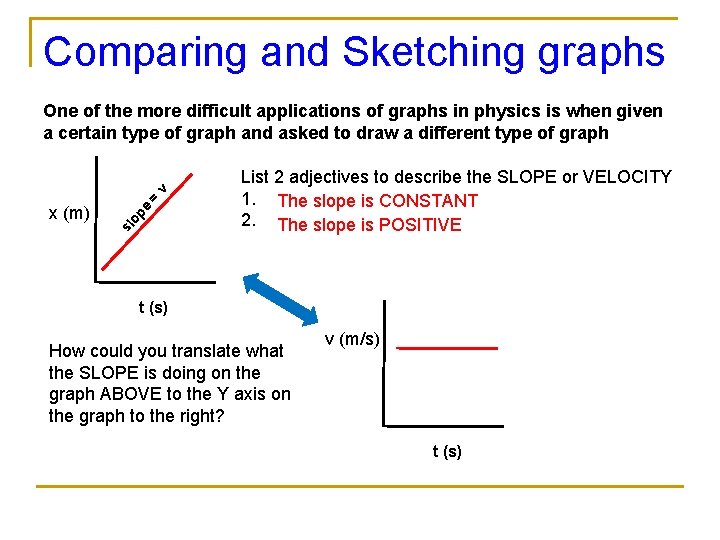
Comparing and Sketching graphs op e sl x (m) = v One of the more difficult applications of graphs in physics is when given a certain type of graph and asked to draw a different type of graph List 2 adjectives to describe the SLOPE or VELOCITY 1. The slope is CONSTANT 2. The slope is POSITIVE t (s) How could you translate what the SLOPE is doing on the graph ABOVE to the Y axis on the graph to the right? v (m/s) t (s)

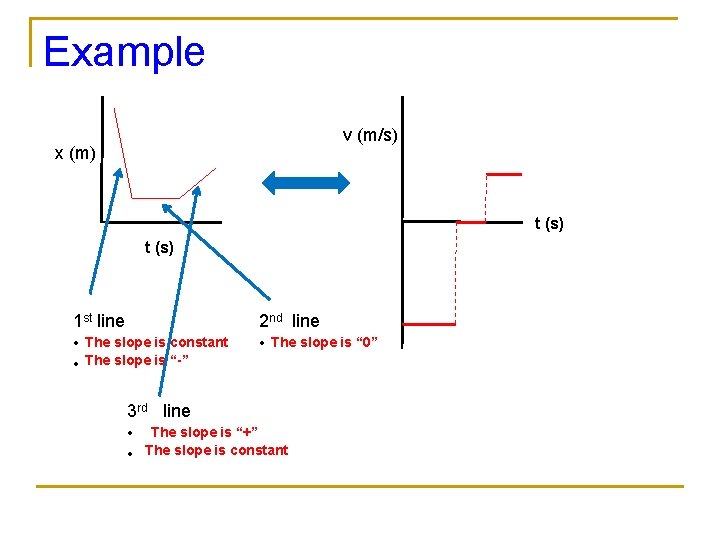
Example v (m/s) x (m) t (s) 1 st line • The slope is constant • The slope is “-” 2 nd line • The slope is “ 0” 3 rd line • The slope is “+” • The slope is constant

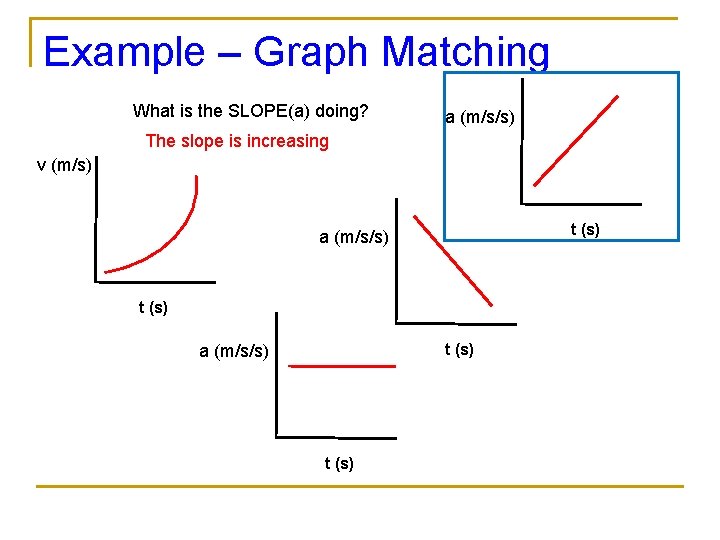
Example – Graph Matching What is the SLOPE(a) doing? a (m/s/s) The slope is increasing v (m/s) t (s) a (m/s/s) t (s)