Methods of Measuring correlation 1 Karl Pearsons coefficient

Methods of Measuring correlation 1. Karl Pearson's coefficient of correlation. 2. Spearman’s rank correlation 3. Scatter diagram

Karl Pearson’s Coefficient of correlation It is very popular method of measuring correlation. since it has been devised By Karl Pearson in 1890 , it is known as Personian coefficient of correlation. It is based on arithmetic mean and standard deviation.

Karl Pearsons coefficient of correlation Calculation of Karl Pearson’s Coefficient of correlation The following methods are used : 1. Actual Mean Method /Direct Method 2. Standard deviation method 3. Assumed mean method/ Indirect /short-cut method

Karl Pearson's co-efficient of correlation • Actual mean method/direct method • Calculate Karl Pearson's coefficient of correlation from the following data: Price (X) Quantity (Y) 10 20 12 29 14 21 16 22 18 28 STEPS: i) Take the deviations of X series from the mean of X and denote these deviations by x ii) Square these deviations and obtain the total, i. e. , ∑x 2 iii) Take the deviations of Y series from the mean of Y and denote these deviations by y iv) Square these deviations and obtain the total, i. e. , ∑y 2 v) Multiply the deviations of X and Y series and obtain the total, i. e. , ∑xy vi) Apply the formula r= å xy åx X å y 2 x = (X - X) y = (Y - Y ) 2

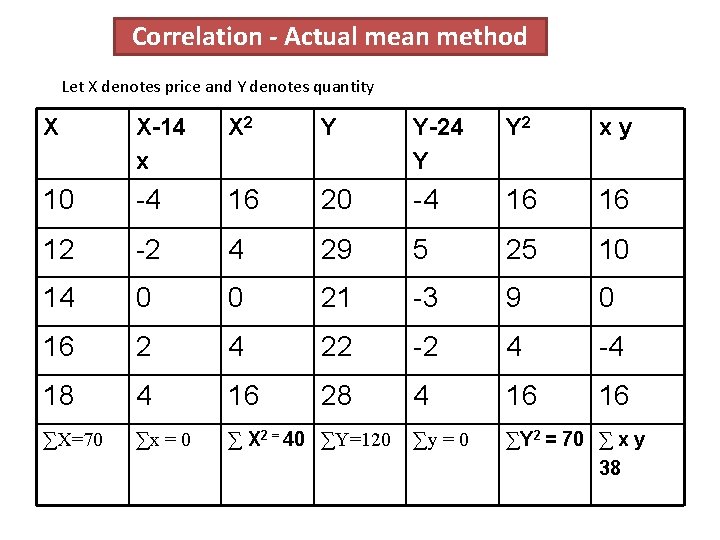
Correlation - Actual mean method Let X denotes price and Y denotes quantity X X-14 x X 2 Y Y-24 Y Y 2 xy 10 -4 16 20 -4 16 16 12 -2 4 29 5 25 10 14 0 0 21 -3 9 0 16 2 4 22 -2 4 -4 18 4 16 28 4 16 16 ∑X=70 ∑x = 0 ∑ X 2 = 40 ∑Y=120 ∑y = 0 ∑Y 2 = 70 ∑ x y 38

Solution actual mean method r = å xy åx å 2 38 = y 2 38 40 70 2800 38 = = 0. 34 r 52. 91

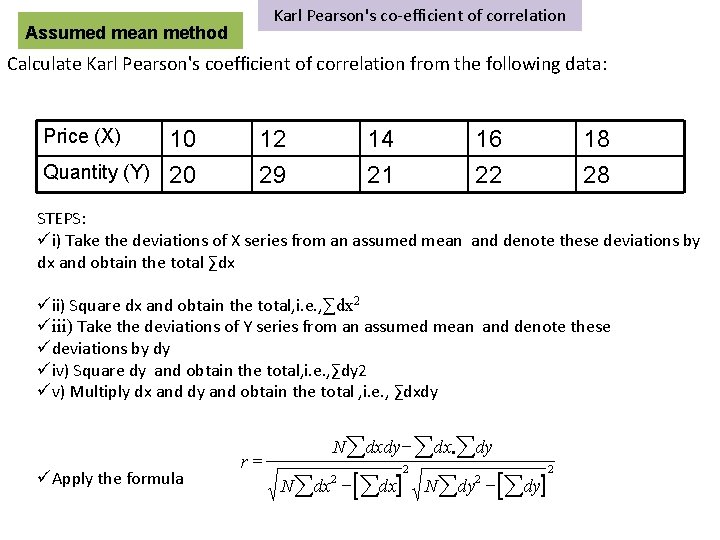
Karl Pearson's co-efficient of correlation Assumed mean method Calculate Karl Pearson's coefficient of correlation from the following data: Price (X) 10 Quantity (Y) 20 12 29 14 21 16 22 18 28 STEPS: üi) Take the deviations of X series from an assumed mean and denote these deviations by dx and obtain the total ∑dx üii) Square dx and obtain the total, i. e. , ∑dx 2 üiii) Take the deviations of Y series from an assumed mean and denote these üdeviations by dy üiv) Square dy and obtain the total, i. e. , ∑dy 2 üv) Multiply dx and dy and obtain the total , i. e. , ∑dxdy üApply the formula r= N ådxdy- ådx. ådy N ådx 2 N ådy 2

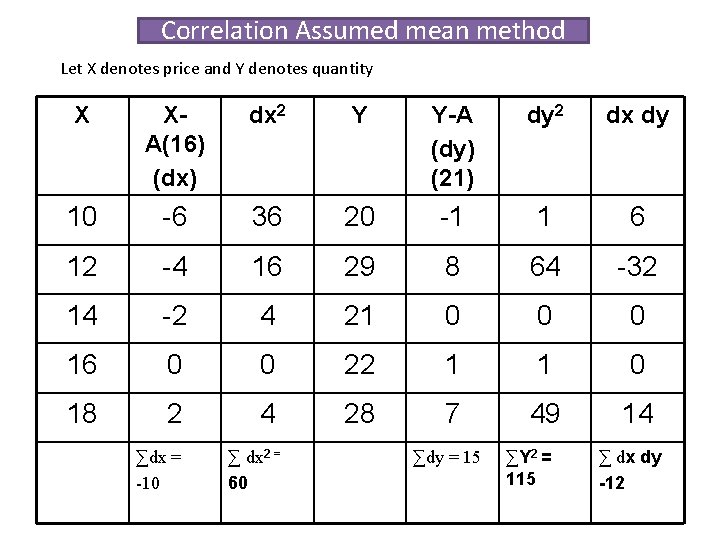
Correlation Assumed mean method Let X denotes price and Y denotes quantity X XA(16) (dx) dx 2 Y Y-A (dy) (21) dy 2 dx dy 10 -6 36 20 -1 1 6 12 -4 16 29 8 64 -32 14 -2 4 21 0 0 0 16 0 0 22 1 1 0 18 2 4 28 7 49 14 ∑dx = -10 ∑ dx 2 = 60 ∑dy = 15 ∑Y 2 = 115 ∑ dx dy -12

Solution - Assumed mean method r= r = r = Nådxdy -ådx. ådy Nådx 2 - ådx 5 X 60 - 2 - 10 Nådy 2 2 - 60 + 150 200 350 90 90 = 264. 57 70000 - 10 ådy 2 X 15 5 X 115 = 0. 34 - 15 2

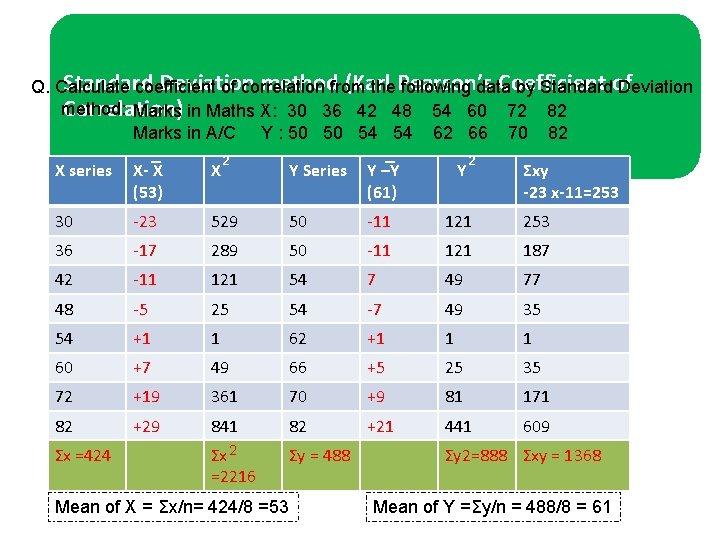
Standard Deviation methodfrom (Karl Coefficient Q. Calculate coefficient of correlation the Pearson’s following data by Standardof Deviation method: Correlation) Marks in Maths X: 30 36 42 48 54 60 72 82 Marks in A/C Y : 50 50 54 54 62 66 70 82 _ _ 2 2 X series X- X X Y Series Y –Y Y Σxy (53) (61) -23 x-11=253 30 -23 529 50 -11 121 253 36 -17 289 50 -11 121 187 42 -11 121 54 7 49 77 48 -5 25 54 -7 49 35 54 +1 1 62 +1 1 1 60 +7 49 66 +5 25 35 72 +19 361 70 +9 81 171 82 +29 841 82 +21 441 609 Σx 2 =2216 Σy = 488 Σx =424 Mean of X = Σx/n= 424/8 =53 Σy 2=888 Σxy = 1368 Mean of Y =Σy/n = 488/8 = 61

Standard Deviation of X & Y Series : S. D. of X = S. D. of Y Σx N = 2 2216 8 Σy 2 N 888 8 Σxy ______ N x σx x σy r = 1368 _______ 8 x 16. 64 x 10. 53 = = 1368 _____ 1401. 75 = 0. 975 High correlation 277 111 = 16. 64 = 10. 58

n a Th u o Y k