Method of manufactured solutions The first stage in

Method of manufactured solutions • The first stage in code verification is to test for problems for which we have analytical solutions. • However, often we have codes that are intended for more complex problems than we can solve analytically. • Codes typically solve differential equations for applied loadings in the form of right hand sides and boundary conditions. • If we cannot solve the differential equation for some representative loading and boundary condition, we can specify a solution, calculate the corresponding loading and boundary conditions, and use them as input to the code.

Beam example • The general equations of a beam loaded by a transverse load q(x) • We want to verify a code that solves this problem for any distribution of EI. • We can start by comparing the solution for constant EI, since for this case it is easy to obtain an analytical solution. • For example, for constant EI and constant q, integrating to obtain a quartic polynomial is very easy, and solution can be found in Mechanics of Materials textbooks.

Manufactured solution for beam • We next want to test code for varying EI, for example EI=cos(x/L) with clamped boundary conditions • Instead of specifying load and trying to find an analytical solution, we will specify the solution w=x 2 and calculate the load • We will now apply this load and check whether our code will produce w=x 2

General procedure (V&CSC 6. 3. 1) 1. Establish the mathematical model in the form L(u)=0, where L() is the differential operator and u is the dependent variable. 2. Choose the analytic form of the manufactured solution um. 3. Operate the mathematical model L onto the manufactured solution um and obtain the analytic source term s=L(um). 4. Obtain the modified mathematical model by including the analytic source term L(u)=s 5. (Mine) check whether the code produces the manufactured solution under the action of s.

Top Hat question • You wrote a code to solve the algebraic equation cosx+7 tan(ln(x))=a For a series of values of a. • What value of a will you test the code on in the spirit of manufactured solutions? • Assume that the equation gives numerical problems to your favorite root solver, and this is why you wrote your own code to solve it.

Remarks • Manufactured solutions do not need to be physically realistic, but care must be taken that they do not crash the code (e. g. square root of negative temperature). • When multiple terms appear in the equations, manufactured solutions should not make one term dominant because this will not verify the other terms. • Trigonometric and exponential functions are good for manufactured solutions because they are infinitely differentiable. • Having a manufactured solution that varies slowly will allow convergence with coarse meshes, hence inexpensive.

Example of MMS with order verification • 6. 3. 4. 1 Steady state heat conduction • A discrete solution described in 6. 3. 4. 1 was proven to have second order convergence, which needed to be verified for the code implementing it. • Manufactured solution that was used • What is needed to generate the manufactured solution besides the source term?

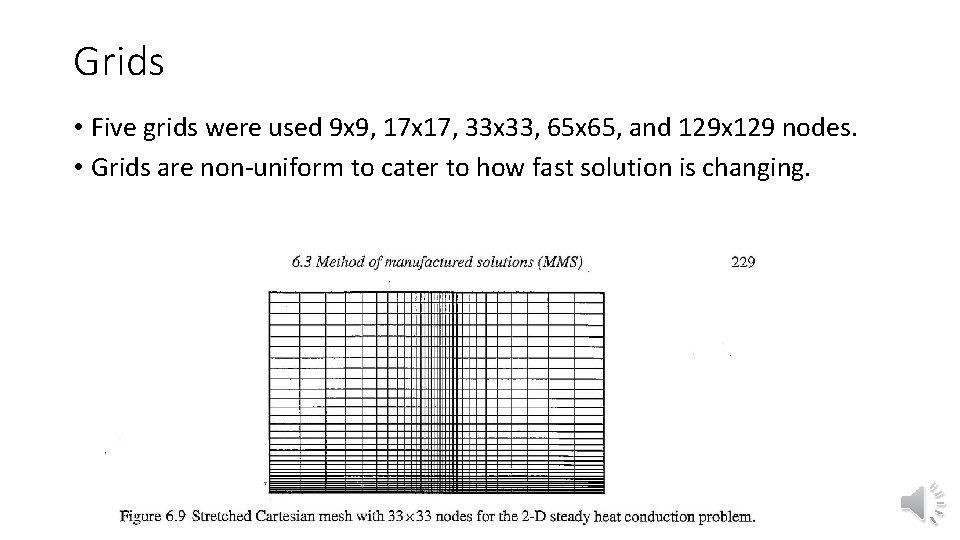
Grids • Five grids were used 9 x 9, 17 x 17, 33 x 33, 65 x 65, and 129 x 129 nodes. • Grids are non-uniform to cater to how fast solution is changing.

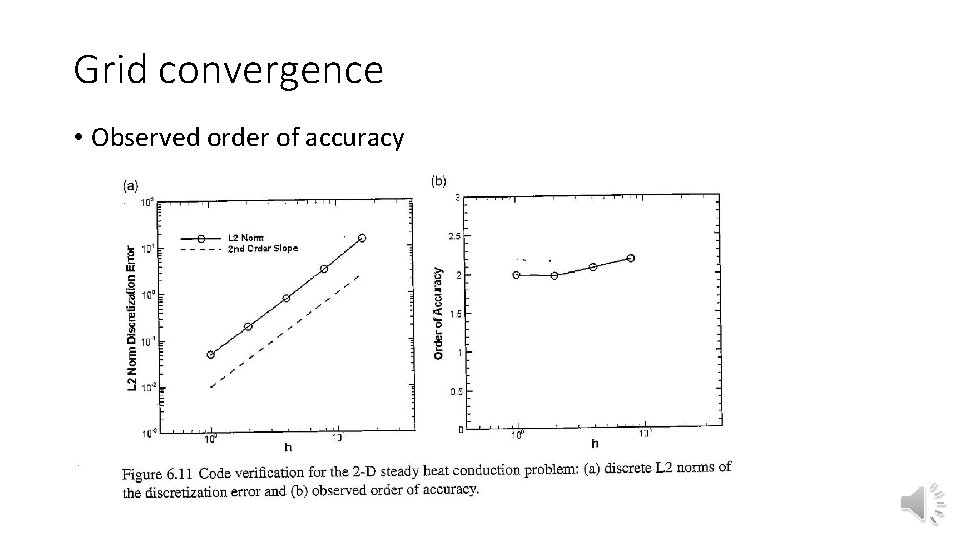
Grid convergence • Observed order of accuracy