Method 2 Resolution into Components Solving Vector Problems

Method #2: Resolution into Components

Solving Vector Problems using the Component Method § § Each vector is replaced by two perpendicular vectors called components. Turn every vector into a right triangle. Add the x-components and the ycomponents to find the x- and ycomponents of the resultant. Use the Pythagorean theorem and the tangent function to find the magnitude and direction of the resultant.

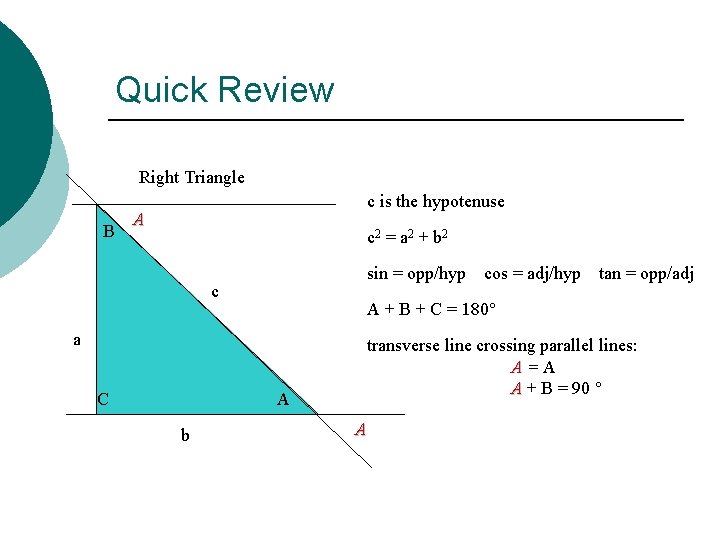
Quick Review Right Triangle B c is the hypotenuse A c 2 = a 2 + b 2 sin = opp/hyp c transverse line crossing parallel lines: A=A A + B = 90 ° A b tan = opp/adj A + B + C = 180° a C cos = adj/hyp A

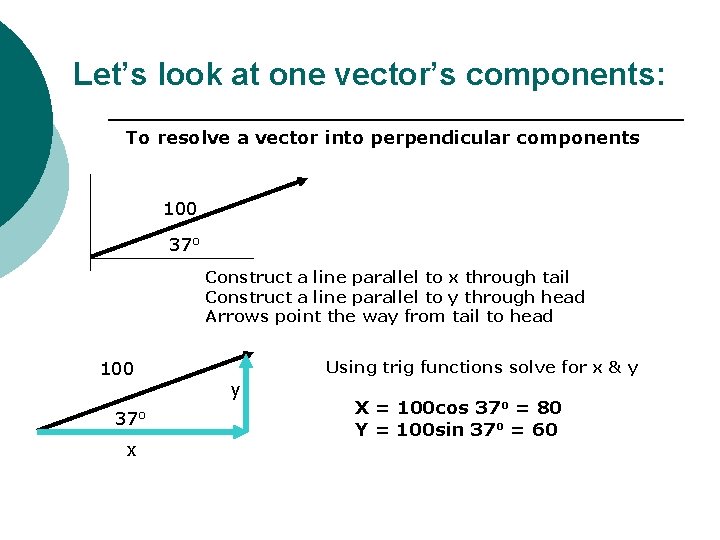
Let’s look at one vector’s components: To resolve a vector into perpendicular components 100 37 o Construct a line parallel to x through tail Construct a line parallel to y through head Arrows point the way from tail to head 100 37 o x Using trig functions solve for x & y y X = 100 cos 37 o = 80 Y = 100 sin 37 o = 60

Why is this important? Components of Force y x

Method #2: Adding Vectors By Resolution into Components USE COLOR PENCILS! Stan is trying to rescue Kyle from drowning. Stan gets in a boat and travels at 6 m/s at 20 o N of E, but there is a current of 4 m/s in the direction of 20 o E of N. Find the velocity of the boat. Don’t measure anything for this method!

Solve the following problem using the component method. 10 km at 30 N of E 6 km at 30 W of N

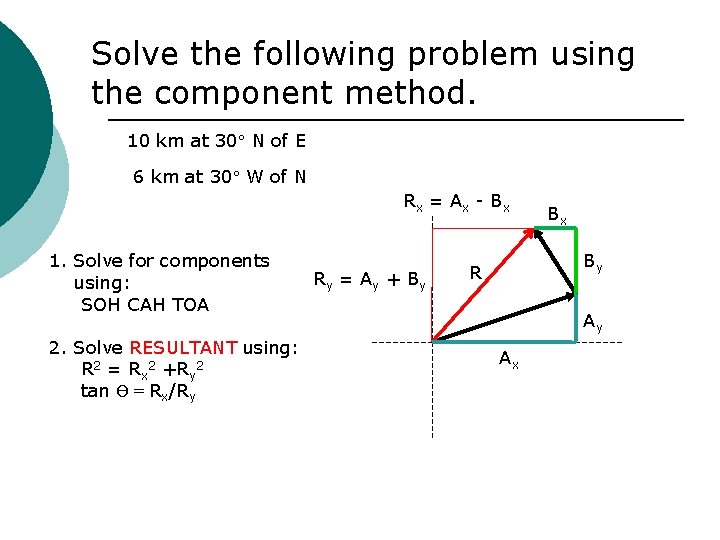
Solve the following problem using the component method. 10 km at 30 N of E 6 km at 30 W of N Rx = A x - B x 1. Solve for components using: SOH CAH TOA 2. Solve RESULTANT using: R 2 = Rx 2 +Ry 2 tan Ө = Rx/Ry Ry = A y + B y Bx By R Ay Ax

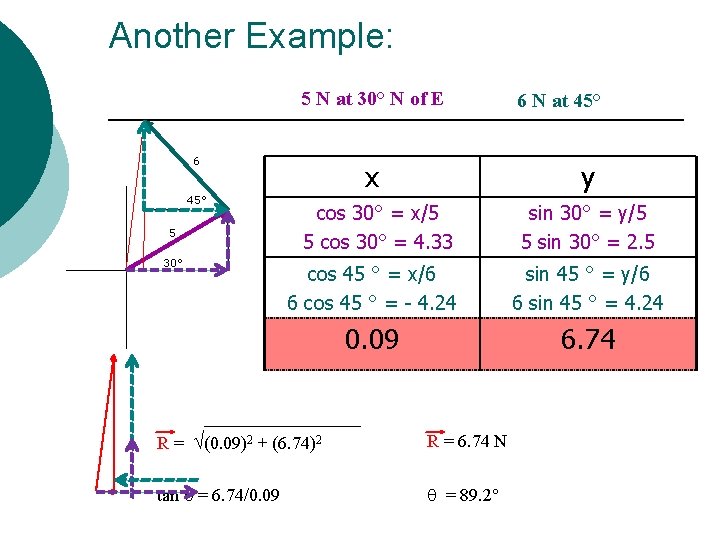
Another Example: 5 N at 30° N of E 6 45° 5 30° x 6 N at 45° y cos 30° = x/5 5 cos 30° = 4. 33 sin 30° = y/5 5 sin 30° = 2. 5 cos 45 ° = x/6 6 cos 45 ° = - 4. 24 sin 45 ° = y/6 6 sin 45 ° = 4. 24 0. 09 6. 74 R = (0. 09)2 + (6. 74)2 R = 6. 74 N tan = 6. 74/0. 09 = 89. 2°

Advantages of the Component Method: § § Can be used for any number of vectors. All vectors are added at one time. Only a limited number of mathematical equations must be used. Least time consuming method for multiple vectors.

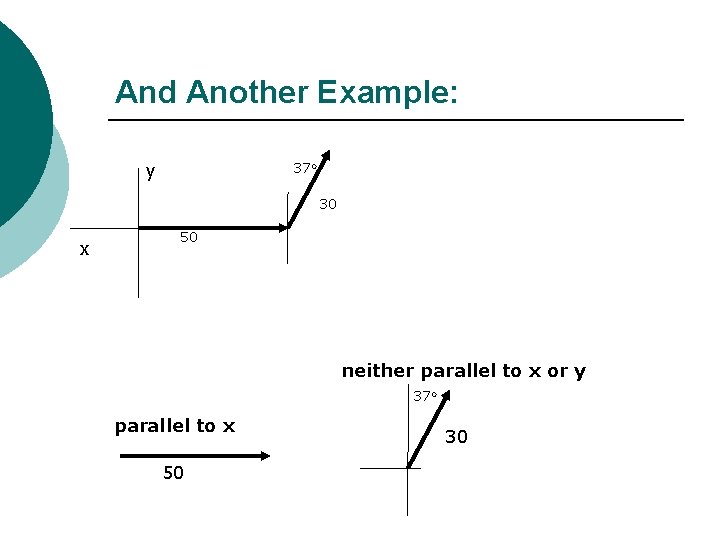
And Another Example: y 37 o 30 x 50 neither parallel to x or y 37 o parallel to x 50 30

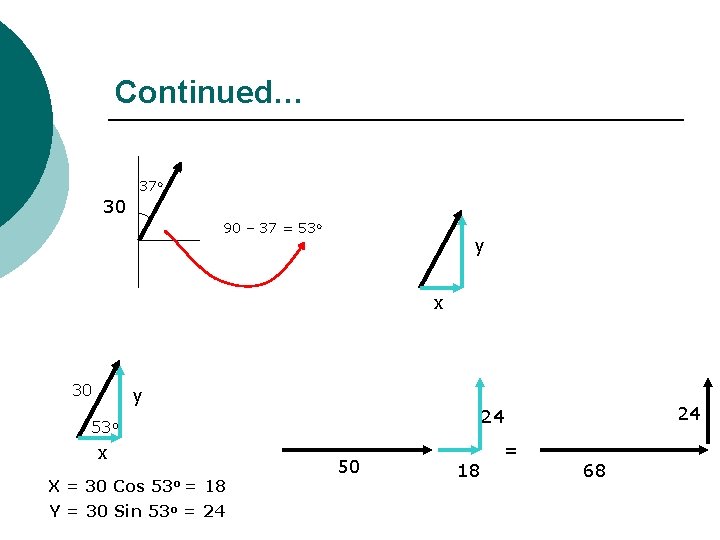
Continued… 37 o 30 90 – 37 = 53 o y x 30 y x X = 30 Cos 24 24 53 o = 18 Y = 30 Sin 53 o = 24 50 18 = 68

Neither Parallel nor Perpendicular Vector Addition (con) For these perpendicular vectors 24 68 Find resultant magnitude & direction R R 2 = 682 + 242 R = 72. 1 θ 24 68 tan θ = 24/68 = tan-1 24/68 = 19. 4 o N of E

This completes Method Two! So lets keep And practice some more! problems #3, 4 due tomorrow