Metda Konench Prvkov vo vrobnch technolgiach prednka 4

Metóda Konečných Prvkov vo výrobných technológiach prednáška č. 4

Obsah prednášky • Rozšírené matice elementu Vektor kódových čísiel • Zostavenie matice konštrukcie • Výpočet primárnych neznámych a reakcií vo väzbách • Jednorozmerná sústava prútov – príklad riešenia • Dvojrozmerná sústava prútov – príklad riešenia • Izoparametrické prvky Odvodenie matíc izoparametrického prútového prvku • Numerická integrácia 2

Zostavenie sústavy rovníc celej konštrukcie Pri zostavení výslednej sústavy rovníc celej úlohy platí pre celkovú potenciálnu energiu sústavy Minimalizáciou potenciálnej energie vzhľadom na posunutia dostaneme výslednú sústavu algebraických rovníc. 3

Rozšírené matice elementu • Sčítavanie potenciálnej energie prvkov a jej minimalizáciu nahradíme výpočtom matice K a vektora f pomocou rozšírených matíc prvku K* a f*. • Rozmer rozšírenej matice prvku je zhodný s rozmerom celkovej matice sústavy • Ak počet globálnych posunutí uzlov prvkov označíme n, bude rozmer celkovej matice sústavy n x n • Členy rozšírenej matice, ktoré nezodpovedajú globálnym posunutiam vybraného prvku sú nulové 4

Rozšírené matice elementu Príklad pre dvojuzlový prvok Pre prvok s globálnymi číslami uzlov {d, m} (tzv. globálne prvkové číslo) výsledný vektor globálnych posunutí uzlov konštrukcie bude (ndof x nbn) x 1 = nbdof x 1 a = [u 1 u 2. . . ud. . . um. . . unbdof] T Potenciálna energia vybraného prvku 5

Rozšírené matice elementu kde rozšírené matice prvku sú 6

Rozšírené matice elementu • Pri tvorbe rozšírených matíc prvkov využívame tzv. vektor kódových čísiel • sú v ňom usporiadané čísla globálnych posunutí uzlových bodov telesa Príklad pre dvojuzlový prvok 7

Zostavenie matice konštrukcie • Matice konštrukcie dostaneme sčítaním rozšírených matíc elementov • Výsledná matica je pásová, symetrická a pozitívne definitná 8

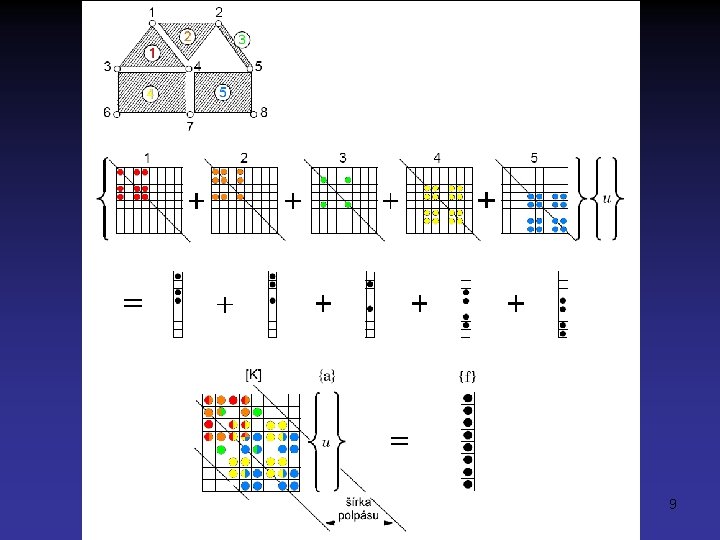
9

Zostavenie matice konštrukcie • šírka polpásu matice sústavy M = (R + 1) v kde R je max. rozdiel čísiel uzlov na prvkoch modelu sústavy v je počet globálnych stupňov voľnosti uzla prvku minimalizácia šírky polpásu = minimalizácia R Zásada: číslovať uzlové body tak, aby rozdiel na prvku (max. a min. číslo uzla) bol minimálny. Pozn. vplyv šírky polpásu na rýchlosť riešenia je závislý na použitej metóde riešenia napr. v prípade Gaussovej eliminačnej metódy. U frontálnej metódy má vplyv napr. rozdiel čísiel uzlov susedných prvkov 10

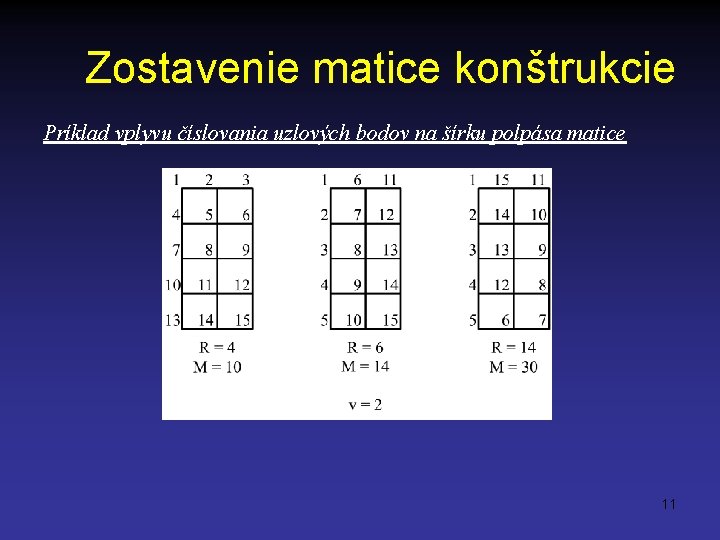
Zostavenie matice konštrukcie Príklad vplyvu číslovania uzlových bodov na šírku polpása matice 11

Zostavenie matice konštrukcie • vzhľadom na symetriu matice sústavy ukladáme iba nenulové členy nad diagonálou a pod tzv. profilom pása matice + diagonálne členy matice K • usporiadavajú sa do poľa pre ušetrenie miesta v pamäti počítača • pásovosť matice možno narušiť nevhodným číslovaním uzlových bodov 12

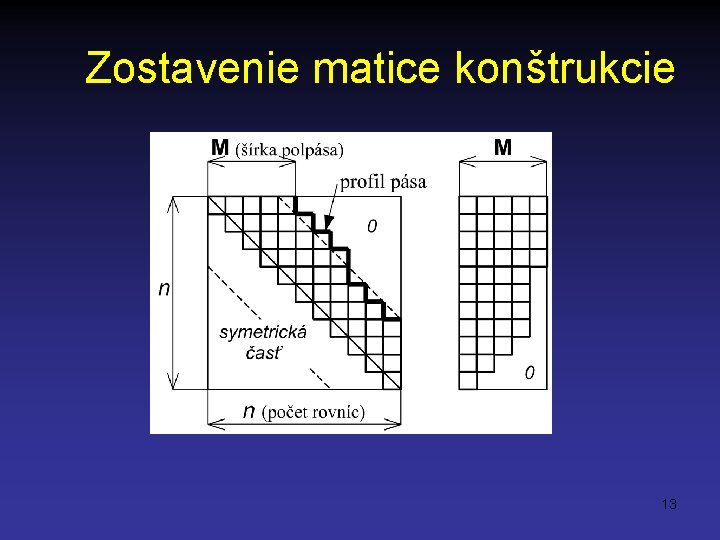
Zostavenie matice konštrukcie 13

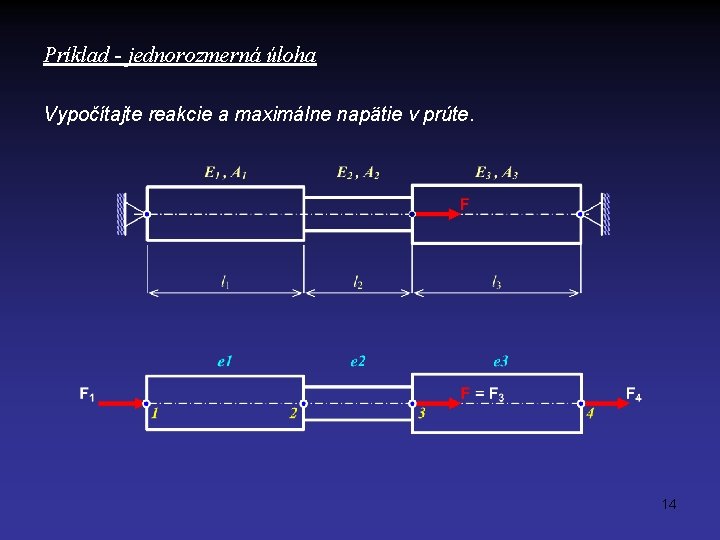
Príklad - jednorozmerná úloha Vypočítajte reakcie a maximálne napätie v prúte. 14

Zostavenie výslednej sústavy rovníc úlohy: Vektor posunutí telesa: a = [u 1 u 2 u 3 u 4] T Okrajové podmienky: u 1 = u 4 = 0 a) Celková potenciálna energia sústavy 15

Minimalizáciou potenciálnej energie vzhľadom na posunutia dostaneme 16

čo v maticovom tvare 17

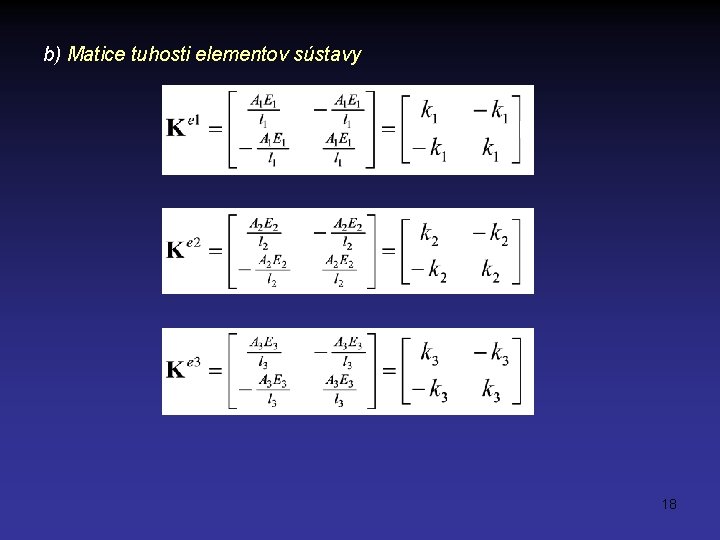
b) Matice tuhosti elementov sústavy 18

Rozšírené matice tuhosti elementov sústavy: 19

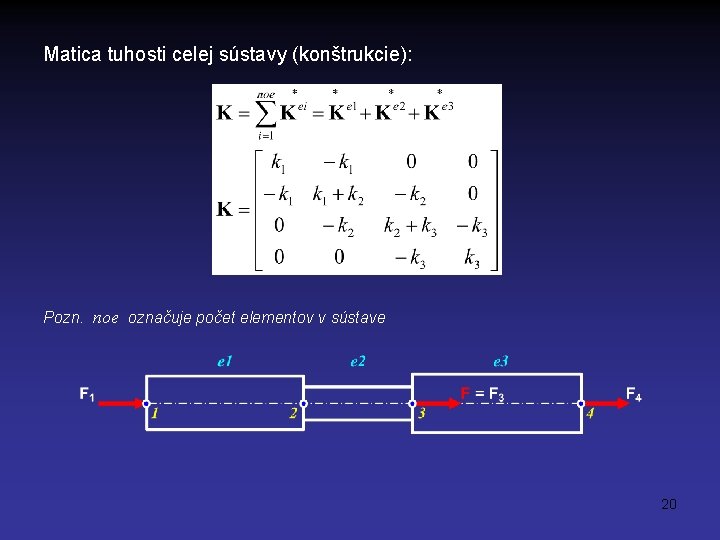
Matica tuhosti celej sústavy (konštrukcie): Pozn. noe označuje počet elementov v sústave 20

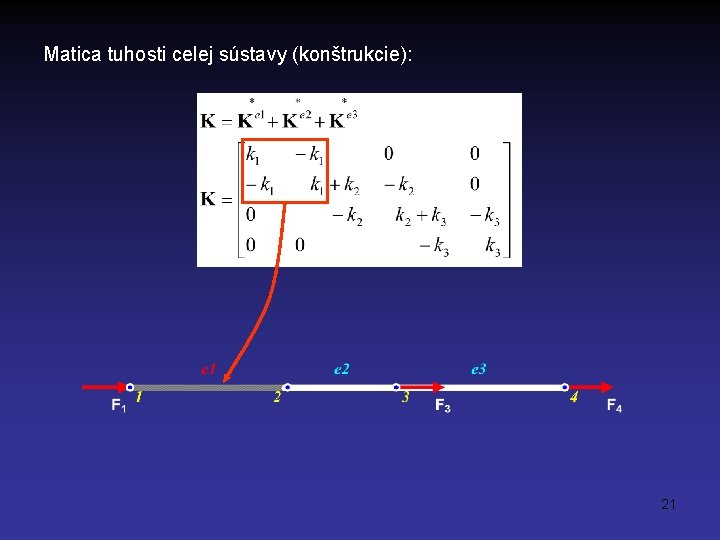
Matica tuhosti celej sústavy (konštrukcie): 21

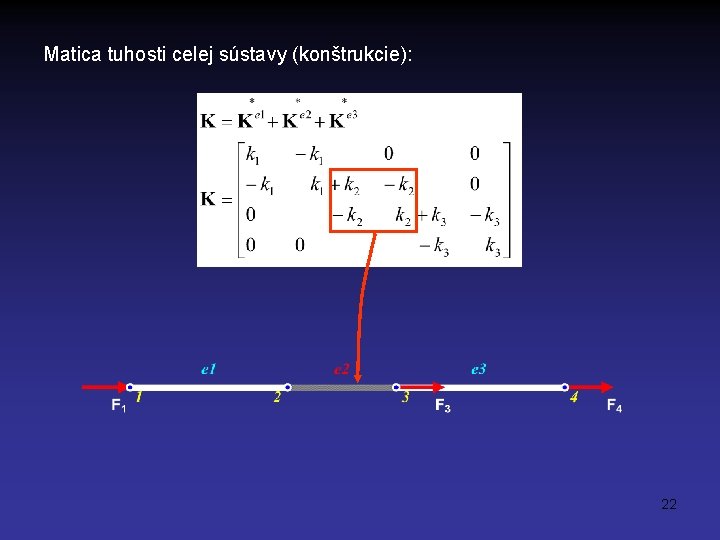
Matica tuhosti celej sústavy (konštrukcie): 22

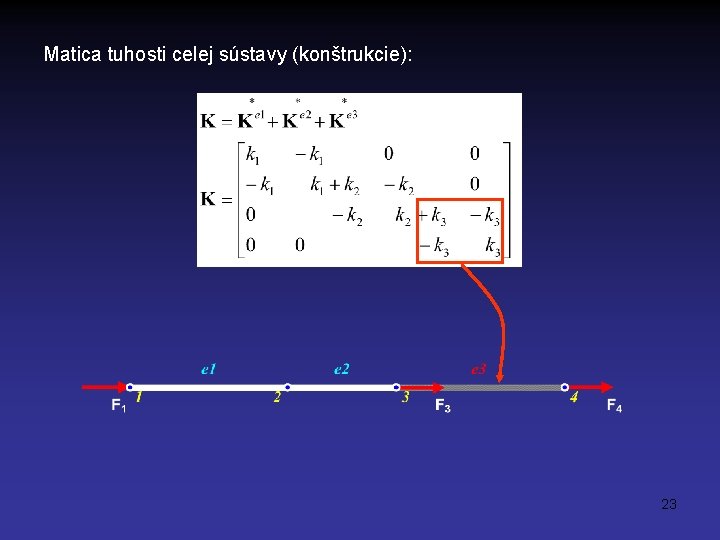
Matica tuhosti celej sústavy (konštrukcie): 23

Matica tuhosti celej sústavy (konštrukcie): Pozn. Symetria matice vyplýva z Maxwell-Bettiho vety o vzájomnosti posunutí. 24

Výsledná sústava rovníc celej konštrukcie pre neupevnené teleso: Matica K je singulárna. Po dosadení okrajových podmienok a do vektora uzlových síl 25

Redukovaná sústava rovníc celej konštrukcie má tvar Výsledné posunutia uzlov 2 a 3 26

Vynechané rovnice pre výpočet reakcií Napätia v elementoch sústavy 27

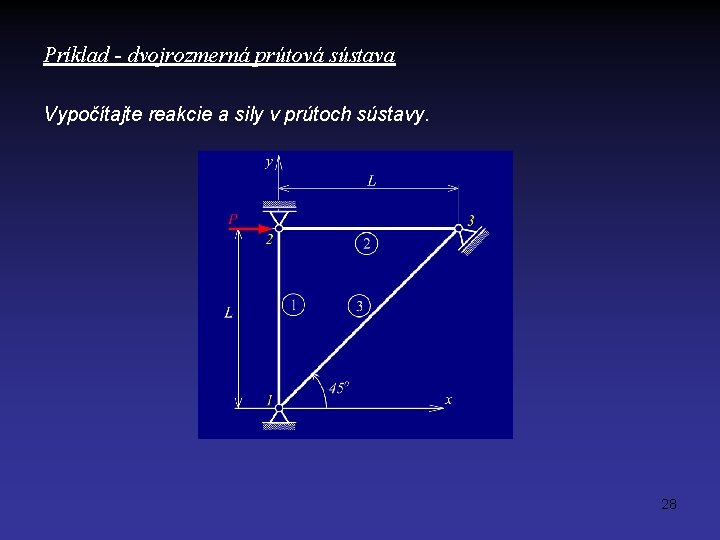
Príklad - dvojrozmerná prútová sústava Vypočítajte reakcie a sily v prútoch sústavy. 28

matice tuhosti prútov v LSS vektory posunutí uzlov v LSS vektory uzlových síl v LSS 29

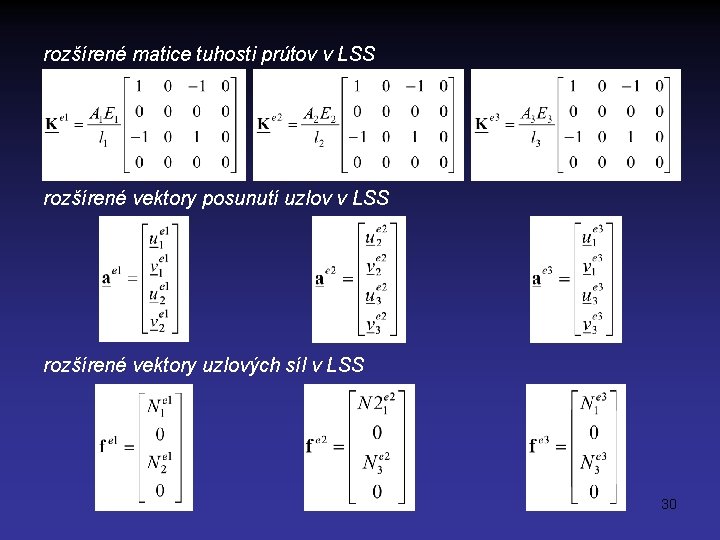
rozšírené matice tuhosti prútov v LSS rozšírené vektory posunutí uzlov v LSS rozšírené vektory uzlových síl v LSS 30

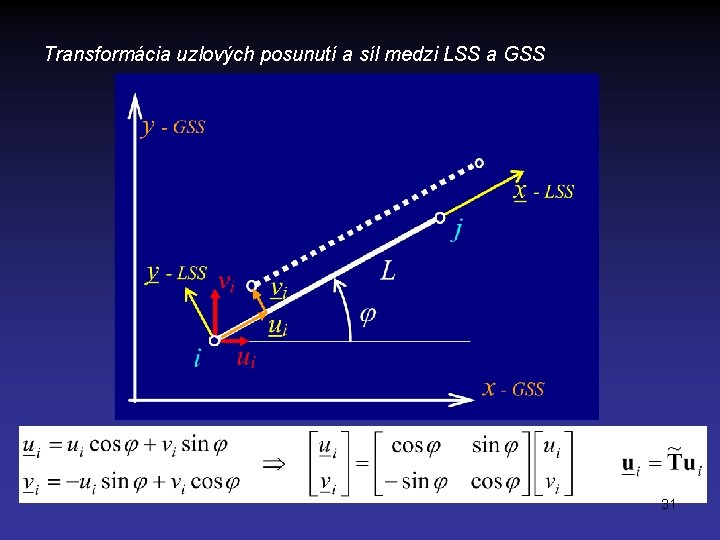
Transformácia uzlových posunutí a síl medzi LSS a GSS 31

Pre dvojuzlový prutový element potom Podobne sú transformované uzlové sily 32

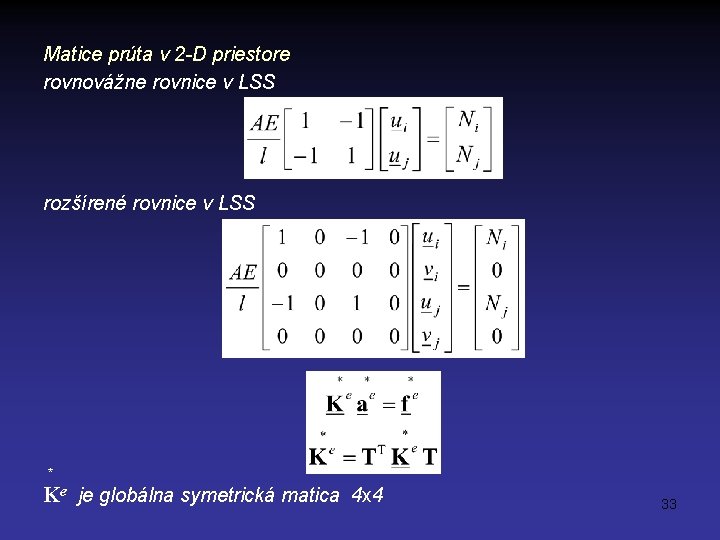
Matice prúta v 2 -D priestore rovnovážne rovnice v LSS rozšírené rovnice v LSS * Ke je globálna symetrická matica 4 x 4 33

transformácia matíc do GSS Prút 1: vektor globálnych posunutí uzlov prvku vektor globálnych uzlových síl transformačná matica 34

globálna matica tuhosti prvku rozšírená matica tuhosti prvku 35

transformácia matíc do GSS Prút 2: vektor globálnych posunutí uzlov prvku vektor globálnych uzlových síl transformačná matica 36

globálna matica tuhosti prvku rozšírená matica tuhosti prvku 37

transformácia matíc do GSS Prút 3: vektor globálnych posunutí uzlov prvku vektor globálnych uzlových síl transformačná matica 38

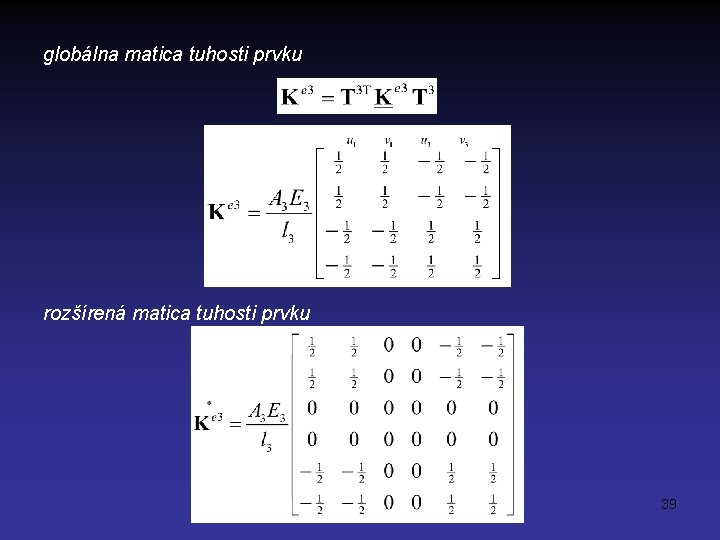
globálna matica tuhosti prvku rozšírená matica tuhosti prvku 39

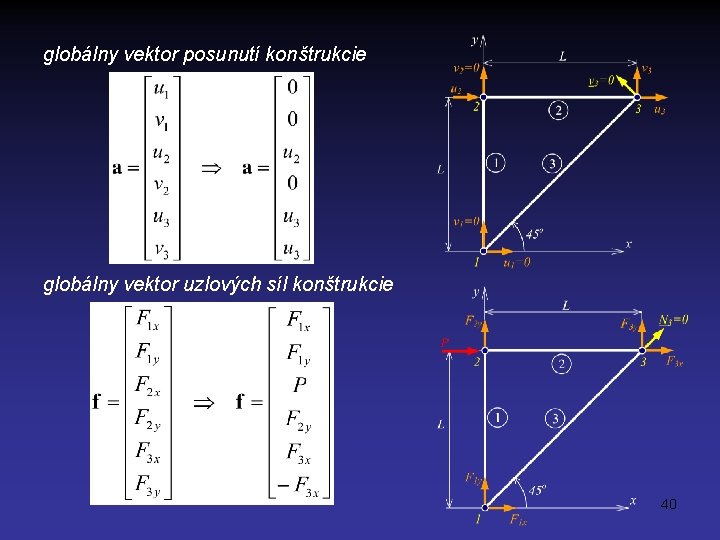
globálny vektor posunutí konštrukcie globálny vektor uzlových síl konštrukcie 40

vzhľadom na okrajové podmienky Pozn. multipoint constraint podobne pre sily 41

Celková globálna matica tuhosti konštrukcie 42

Výpočet primárnych neznámych a reakcií vo väzbách Výslednú sústavu rovníc celej konštrukcie upravíme do tvaru kde: aa sú neznáme zložky uzlových posunutí ab sú známe zložky uzlových posunutí fa sú známe (zaťažujúce) sily v uzloch fb sú neznáme reakcie vo väzbách 43

Potom neznáme uzlové posunutia aa vypočítame z rovníc a neznáme reakcie fb Úloha sa výrazne zjednoduší ak ab = 0 t. j. v uzloch sú tuhé upevnenia 44

Izoparametrické prvky Dôvody zavedenia a používania izoparametrických elementov: • modelovanie zložitých telies so zakriveným povrchom, • problémy s integráciou cez objem a povrch zložitých telies Princíp IE: • využívajú vlastnosti a možnosti transformácie bodov oblasti (objemu) na iný jednoduchší (normalizovaný) tvar, • objemová, resp. plošná integrácia sa potom vykonáva na tejto normalizovanej tzv. jednotkovej oblasti, • transformácia musí byť pritom jednoznačná (každému bodu pôvodnej oblasti jednoznačne prislúcha jeden bod normalizovanej oblasti a naopak). 45

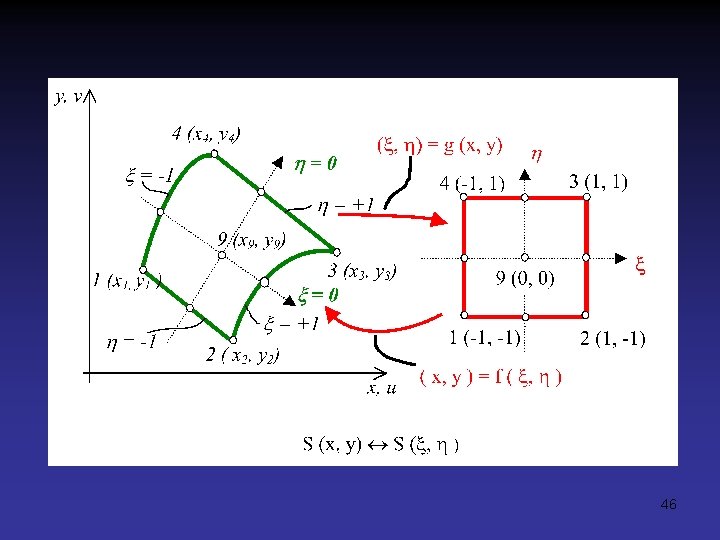
46

Izoparametrické prvky Pre transformáciu súradníc ľubovolného bodu platí teda kde Ni( ) sú tvarové funkcie vyjadrené v prirodzených súradniciach 47

Izoparametrické prvky ktoré musia spĺňať okrajové podmienky Ak = 1 = 0 : : atď. . x( ) = x 3 y( ) = y 3 x( ) = x 9 y( ) = y 9 48

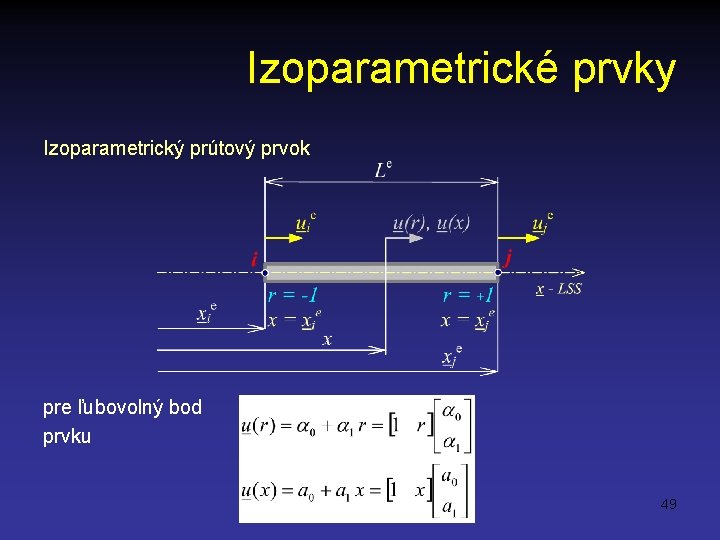
Izoparametrické prvky Izoparametrický prútový prvok pre ľubovolný bod prvku 49

Izoparametrické prvky pre posunutia uzlových bodov potom posunutie ľubovolného bodu prvku 50

Izoparametrické prvky vzťah medzi súradnicou x a prirodzenou súradnicou r 51

Izoparametrické prvky pomerná deformácia prvku kde J je Jakobián (Jakobiho matica) zobrazenia, zabezpečujúci vzťah medzi globálnymi a prirodzenými súradnicami. 52

Izoparametrické prvky lokálna matica tuhosti prvku Pre zložitejšie prvky sa integrácia v matici tuhosti robí numericky, napr. pomocou Gaussovej kvadratúry. 53

Izoparametrické prvky Delenie izoparametrických prvkov • subparametrické prvky pri ktorých sú pre transformáciu súradníc uzlov použité tvarové funkcie nižšieho rádu ako pre transformáciu posunutí • izoparametrické prvky pri ktorých sú pre transformáciu súradníc uzlov použité rovnaké tvarové funkcie ako pre transformáciu posunutí • superparametrické prvky pri ktorých sú pre transformáciu súradníc uzlov použité tvarové funkcie vyššieho rádu ako pre transformáciu posunutí 54

Numerická integrácia funkcie jednej premennej • vyčíslovanie integrálov pri výpočte matíc prvku pri použití prirodzených súradníc sa vykonáva vždy na rovnakej oblasti s jednotkovými hranicami • preto je možné pre výpočet použiť numerickú integráciu • najčastejšie sa používa metóda Gaussovej kvadratúry 55

Numerická integrácia Majme integrál Integrál počítame tak, že hodnotu funkcie f v niekoľkých vybraných bodoch (tzv. integračných bodoch) vynásobíme ich váhovými súčiniteľmi w a sčítame navzájom: 56

Numerická integrácia Pri Gaussovej metóde je poloha bodov i zvolená symetricky od stredu intervalu tak, aby bola dosiahnutá maximálna presnosť integrácie. 57

Numerická integrácia Vo všeobecnosti platí: ak použijeme n integračných bodov, dostaneme exaktný výsledok pre polynóm stupňa 2 n-1 a nižší 58

59