Metamorphic Exploration of an Unsupervised Clustering Program Sen

Metamorphic Exploration of an Unsupervised Clustering Program Sen Yang, Dave Towey School of Computer Science, University of Nottingham Ningbo China, Zhejiang, People’s Republic of China dave. towey@nottingham. edu. cn Zhi Quan Zhou Institute of Cybersecurity and Cryptology, University of Wollongong, NSW 2522, Australia

Acknowledgements • UNNC Fo. SE • UNNC IDIC • … and others • Thank you to Sen for drafting the PPTs

UNNC China UK Malaysia

UNNC • University of Nottingham Ningbo China • First Sino-foreign University • Established in 2004 • English Medium of Instruction (EMI) • About 8, 000 students • ~10% international • More than 750 staff (academic and professional) • From more than 70 countries and regions around the world • “An innovation, and centre for innovation”

Background I • The oracle problem makes it difficult to test Machine Learning (ML) software • There also many (potential) ML users who are not expert, due to ML’s popularity • Most related research is about supervised ML

Background II • Evaluating the quality of clustering algorithms can be challenging • No label for validation • Users’ subjective expectations matter a lot • MT can alleviate the oracle problem

Background III • ML has been applied in numerous industrial domains, including: • Medical, Economy, Automated driving, Decision making, … Supervised ML (Classification problem) • ML algorithm Unsupervised ML (Clustering problem)

Metamorphic Testing • The idea: • It is possible to identify relationships amongst multiple inputs and outputs for a software under test (SUT), even if we don’t know the correctness of individual outputs • Metamorphic Relations (MRs) are the necessary properties of the SUT

Metamorphic Exploration • Recently, MRs have been applied to enhance system understanding and use • These “MRs” need not be necessary properties for software correctness • They can be hypothesized by the users • Call them “Hypothesized MRs” (HMRs)

Our Study • A case study of metamorphic exploration using a clustering program • Weka, one of the most popular data science platforms for ML and data mining • K-means Clustering Algorithm

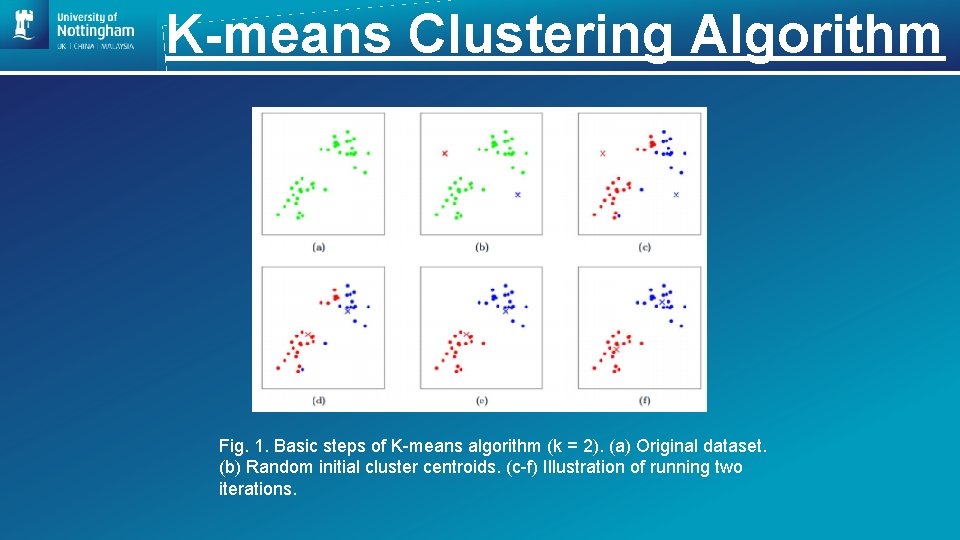
K-means Clustering Algorithm • Attempts to (iteratively) partition a dataset into K distinct non-overlapping subgroups (clusters) where each data point belongs to one and only one group • Aims to minimize the following cost function (sum of the squared error) X = {xi}, i = 1, …, n be the set of n d-dimensional points to be clustered into a set of K clusters, C = {ck}, k = 1, …, K. Let μk be the mean of cluster ck.

K-means Clustering Algorithm Fig. 1. Basic steps of K-means algorithm (k = 2). (a) Original dataset. (b) Random initial cluster centroids. (c-f) Illustration of running two iterations.

Hypothesised MRs • HMR 1: Translation of 2 D points along a line parallel to the x- or y-axis should not have an impact on the clustering results • HMR 2: Adding a duplicate point should not have an impact on the clustering results • HMR 3: Moving an existing point towards the cluster center should not have an impact on the clustering results • HMR 4: Adding a dimension in which all points have an equal value should not have an impact on the clustering results. • HMR 5: Swapping the x- and y-coordinates of each and every point (which is essentially conducting a geometric transformation on the existing points) should not have an impact on the clustering results • HMR 6: Using the same set of points while changing their input order to the SUT should not have an impact on the clustering results • HMR 7: In 2 D, flipping the data points along one (x- or y-) axis should not have an impact on the clustering results

Hypothesised MRs • HMR 1: Translation of 2 D points along a line parallel to the x- or y-axis should not have an impact on the clustering results • HMR 2: Adding a duplicate point should not have an impact on the clustering results • HMR 3: Moving an existing point towards the cluster center should not have an impact on the clustering results • HMR 4: Adding a dimension in which all points have an equal value should not have an impact on the clustering results. • HMR 5: Swapping the x- and y-coordinates of each and every point (which is essentially conducting a geometric transformation on the existing points) should not have an impact on the clustering results • HMR 6: Using the same set of points while changing their input order to the SUT should not have an impact on the clustering results • HMR 7: In 2 D, flipping the data points along one (x- or y-) axis should not have an impact on the clustering results

Set-up • Applied the approach on implementations of K-means clustering algorithm in Weka 3. 8. 3 • Initial test cases (single test case): • Iris. 2 D. arff data • Default setting with K=5, S=10 • Manually manipulated the follow-up test cases

(Preliminary) Results

(Preliminary) Results

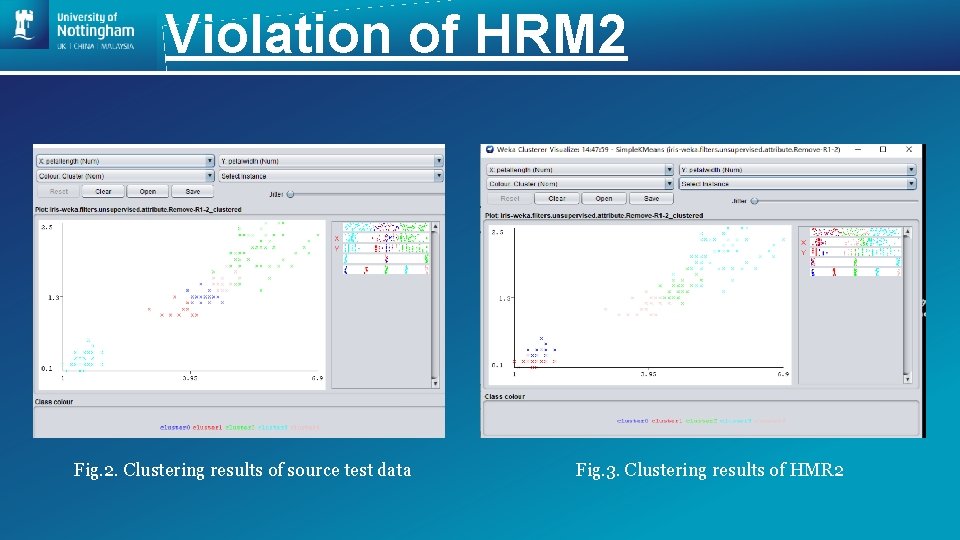
Violation of HRM 2 Fig. 2. Clustering results of source test data Fig. 3. Clustering results of HMR 2

(Preliminary) Results

(Preliminary) Results

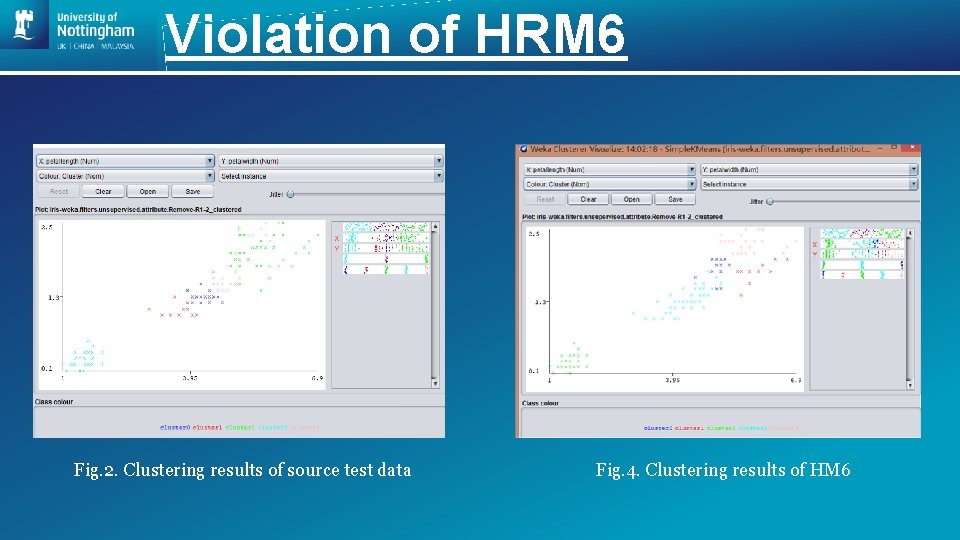
Violation of HRM 6 Fig. 2. Clustering results of source test data Fig. 4. Clustering results of HM 6

Analysis & Discussion • Adding a new data point leads to a new round of calculation of the Euclidean distance when re-locating the new cluster centroids • This will also influence the selection of initial cluster center points • Changing of the data entry order will have impact on the clustering results

Analysis & Discussion • This reflects a characteristic of the K-means clustering algorithm itself, and is not a defect in the implementation • K-means algorithm is sensitive to the selection of initial clustering centroid

Analysis & Discussion

Recommendation • If the user needs to add new data containing some duplicates to the original dataset, then it is better to choose a hierarchical clustering algorithm, to keep a stable clustering performance • If we want to re-generate an earlier test result, we should keep the original order of the data points when they are entered into the system

Sen’s Conclusion • Compared with the understanding of the SUT before the experiment, now have gained new knowledge and understanding of the system • ME can be used to help users explore the system • ME can be used to guide users to better use the algorithm

Discussion & Future Work • Opportunity to embrace ME as a step towards MT • Undergraduate curricula, and elsewhere • Metamorphic Exploration (Journal First): • Thursday 30 May 15: 10, Van-Horne

Thank you!

Q&A