Mestrado em Informtica Alguns conceitos de Teoria dos

Mestrado em Informática Alguns conceitos de Teoria dos Grafos para Fluxo em Redes Maria Claudia Silva Boeres boeres@inf. ufes. br Teoria dos Grafos UFES

Motivação • Definições e terminologias usadas em diferentes formulações e algoritmos de fluxo em redes Teoria dos Grafos UFES

Discutiremos. . . • Definições e terminologias de Teoria dos Grafos para fluxo em redes • Estruturas de Dados para representação de Redes • Transformações de modelos de problemas de fluxo em redes Teoria dos Grafos UFES

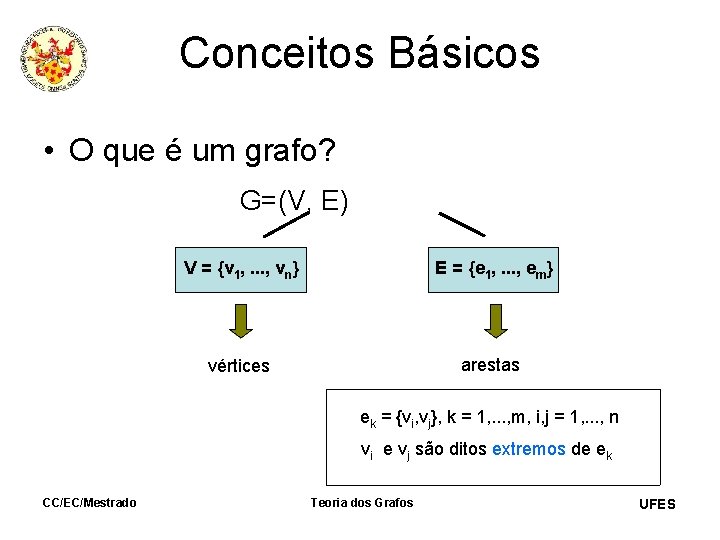
Conceitos Básicos • O que é um grafo? G=(V, E) V = {v 1, . . . , vn} E = {e 1, . . . , em} vértices arestas ek = {vi, vj}, k = 1, . . . , m, i, j = 1, . . . , n vi e vj são ditos extremos de ek CC/EC/Mestrado Teoria dos Grafos UFES

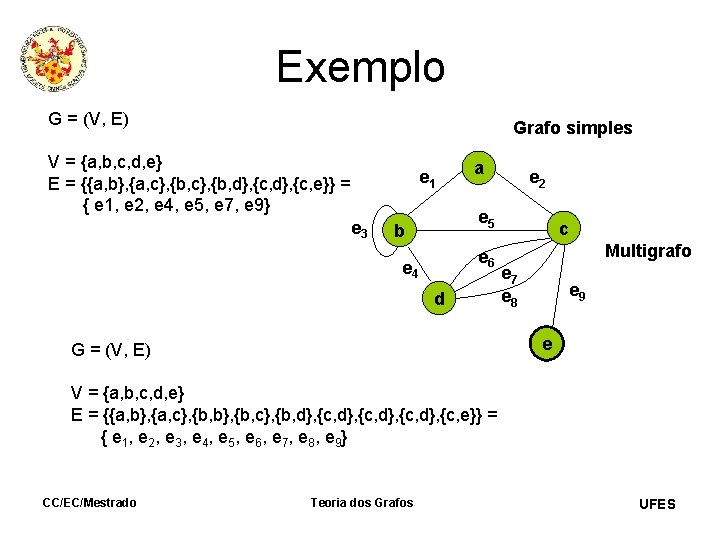
Exemplo G = (V, E) Grafo simples V = {a, b, c, d, e} E = {{a, b}, {a, c}, {b, d}, {c, e}} = { e 1, e 2, e 4, e 5, e 7, e 9} e 3 e 1 a e 2 e 5 b e 6 e 4 d c Multigrafo e 7 e 8 e 9 e G = (V, E) V = {a, b, c, d, e} E = {{a, b}, {a, c}, {b, b}, {b, c}, {b, d}, {c, e}} = { e 1, e 2, e 3, e 4, e 5, e 6, e 7, e 8, e 9} CC/EC/Mestrado Teoria dos Grafos UFES

Conceitos • Uma aresta do tipo {vi, vi} é denominada laço. – A aresta e 3 do exemplo anterior é um laço. • Arestas que possuem os mesmos vértices extremos são ditas paralelas. – As arestas e 6, e 7 e e 8 do exemplo anterior são paralelas. • Um grafo que possui arestas paralelas é denominado multigrafo. • Um grafo sem laços nem arestas paralelas é denominado grafo simples. CC/EC/Mestrado Teoria dos Grafos UFES

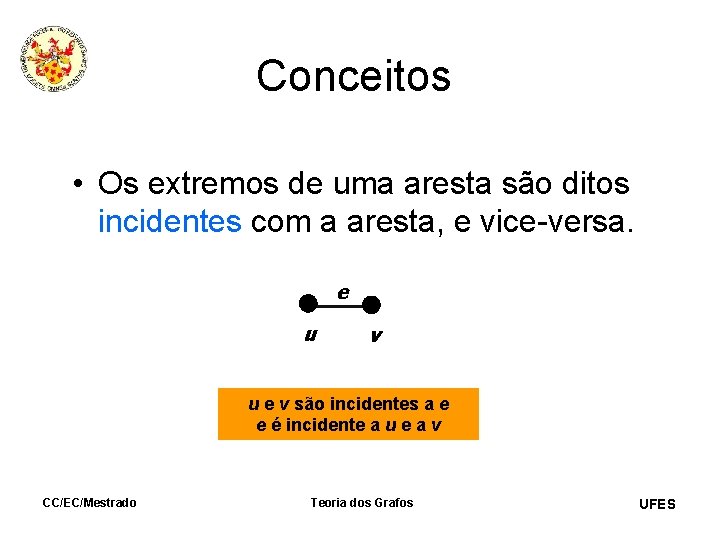
Conceitos • Os extremos de uma aresta são ditos incidentes com a aresta, e vice-versa. e u v u e v são incidentes a e e é incidente a u e a v CC/EC/Mestrado Teoria dos Grafos UFES

Conceitos • Dois vértices que são incidentes a uma mesma aresta são ditos adjacentes. e u e v são adjacentes u v • Duas arestas que são incidentes a um mesmo vértice são ditas adjacentes. e 1 e e 2 são adjacentes u CC/EC/Mestrado Teoria dos Grafos e 2 UFES

Observação O conceito de incidência ou adjacência é importante para a representação da estrutura de um grafo como um diagrama CC/EC/Mestrado Teoria dos Grafos UFES

Conceitos • O número de vértices de um grafo G é denotado por n = |V|. O valor n também é conhecido como ordem de G • O número de arestas de um grafo é denotado por m = |E| • Se n e m são finitos, o grafo é finito. Caso contrário é dito infinito. – Exemplo de grafo infinito: malhas CC/EC/Mestrado Teoria dos Grafos UFES

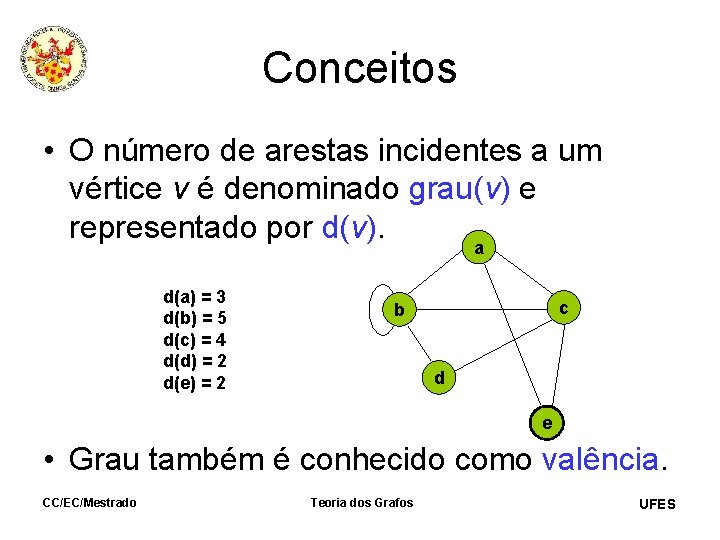
Conceitos • O número de arestas incidentes a um vértice v é denominado grau(v) e representado por d(v). a d(a) = 3 d(b) = 5 d(c) = 4 d(d) = 2 d(e) = 2 c b d e • Grau também é conhecido como valência. CC/EC/Mestrado Teoria dos Grafos UFES

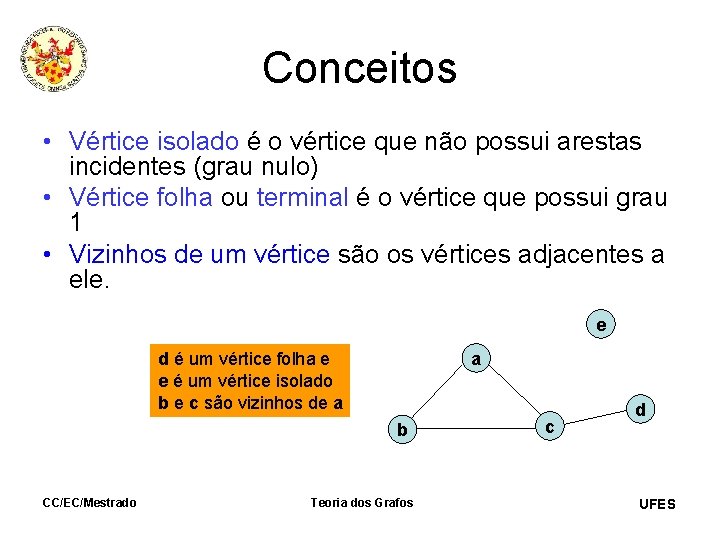
Conceitos • Vértice isolado é o vértice que não possui arestas incidentes (grau nulo) • Vértice folha ou terminal é o vértice que possui grau 1 • Vizinhos de um vértice são os vértices adjacentes a ele. e a d é um vértice folha e e é um vértice isolado b e c são vizinhos de a b CC/EC/Mestrado Teoria dos Grafos c d UFES

Conceitos • Pares de vértices (ou de arestas) não adjacentes são denominadas independentes. • Um conjunto de vértices (ou arestas) é independente se nenhum par de seus elementos é adjacente. CC/EC/Mestrado Teoria dos Grafos UFES

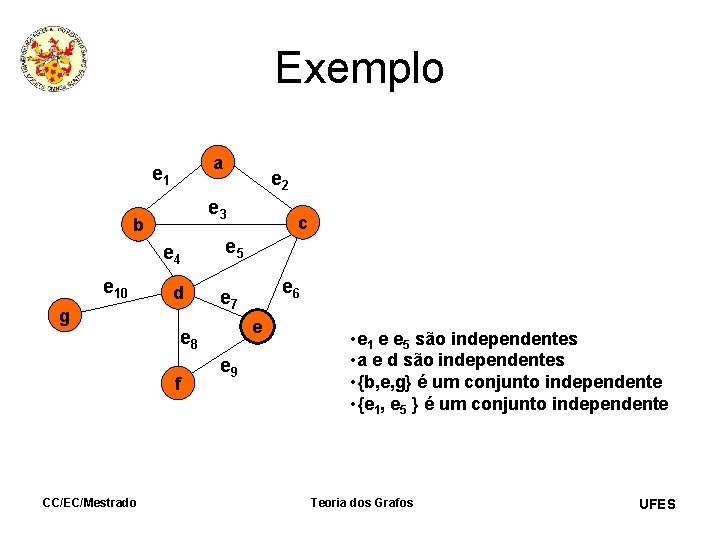
Exemplo a e 1 e 3 b e 4 e 10 e 2 d g e 5 CC/EC/Mestrado e 6 e 7 e e 8 f c e 9 • e 1 e e 5 são independentes • a e d são independentes • {b, e, g} é um conjunto independente • {e 1, e 5 } é um conjunto independente Teoria dos Grafos UFES

Teorema 1: Seja G = (V, E) um grafo simples com n vértices e m arestas. Então ∑ d(v) = 2 m vЄV Prova: • A aresta e é incidente aos vértices v e w e u CC/EC/Mestrado v • É contabilizada no cômputo do grau de v e também de w. Teoria dos Grafos UFES

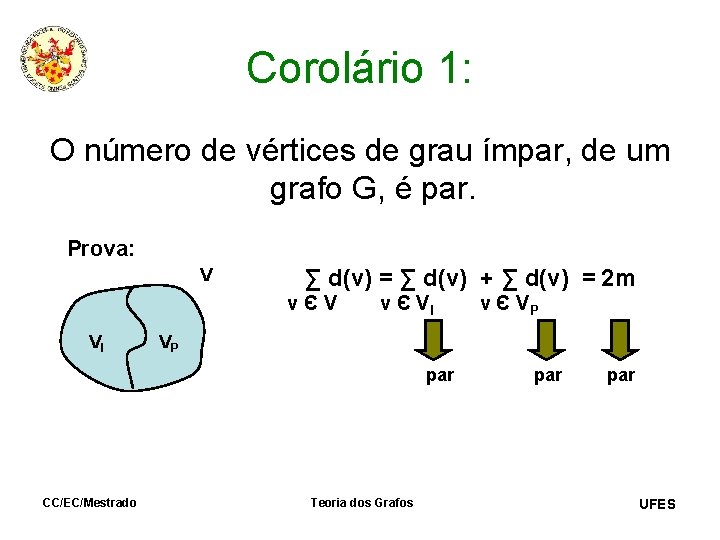
Corolário 1: O número de vértices de grau ímpar, de um grafo G, é par. Prova: V ∑ d(v) = ∑ d(v) + ∑ d(v) = 2 m vЄV VI v Є VI VP par CC/EC/Mestrado v Є VP Teoria dos Grafos par UFES

Subgrafos Subgrafo: G' = (N', A') é um subgrafo de G = (N, A) se N' N e A' A. Subgrafo induzido por N': G' = (N', A') é um subgrafo de G = (N, A) induzido por N' se G' contém todos os arcos de G que ligam apenas os vértices de N'. • Subgrafo gerador: o subgrafo G' = (N', A') de G = (N, A) é gerador se N' = N e A' A. UFES

Percursos Percurso: é um subgrafo de G = (N, A) que consiste de vértices e arcos em uma sequência i 1 – a 1 – i 2 – a 2 – i 3 – a 3 - … - ir-1 – ir, que satisfaz a seguinte propriedade: k, 1 k r-1, ak = (ik, ik+1) A ou ak = (ik+1, ik) A. Percurso direcionado: todos os arcos do percurso estão na mesma direção. Percurso simples direcionado: étodos os arcos do percurso direcionado não se repetem, podendo haver repetição de vértices. • Caminho: percurso simples sem repetição de vértices. • Caminho direcionado: percurso simples direcionado sem repetição de vértices. UFES

Percursos Ciclo: percurso simples e fechado (o nó inicial coincide com o final). Ciclo direcionado: ciclo orientado com todos os arcos na mesma direção. Rede acíclica: um grafo é acíclico se não contém ciclo direcionado. UFES

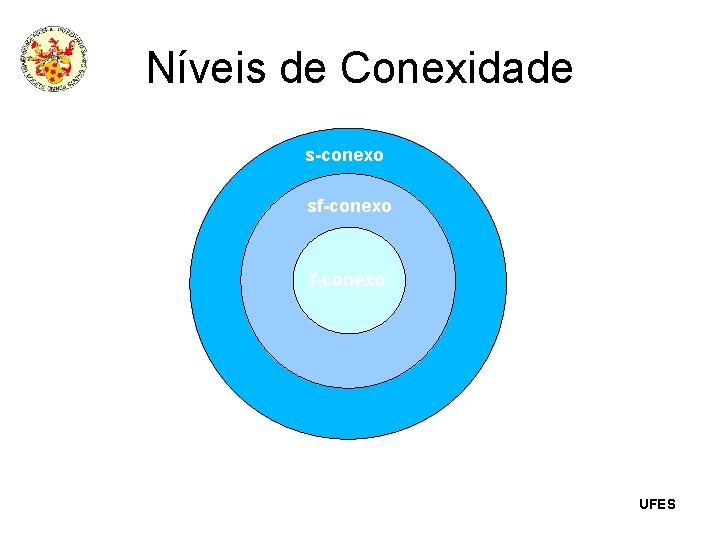
Conexidade Dois vértices estão conectados se existe um caminho entre eles. Um grafo é conexo se todo par de vértices é conectado. Caso contrário é desconexo. Grafo simplesmente conexo ou s-conexo: todo par de vértices é unido por ao menos um caminho no grafo correspondente não direcionado. Grafo semi-fortemente conexo ou sf-conexo: em todo par de vértices do grafo, um deles é atingível a partir do outro (ou seja, entre eles existe um caminho em ao menos um dos dois sentidos possíveis) Grafo fortemente conexo ou f-conexo: todo par de vértices é mutuamente atingível, ou seja, a todo par de vértices está associado um par de caminhos de sentidos opostos. Todo vértice é atingível a partir de um vértice dado e todo vértice atinge todo vértice dado UFES

Exemplos a a c b d d a c b d UFES

Níveis de Conexidade s-conexo sf-conexo UFES

Componentes f-conexas • Um grafo orientado qualquer pode ser particionado em componentes f-conexas maximais. • Se um grafo orientado é f-conexo: a partição é o próprio conjunto de vértices do grafo. UFES

Corte de arcos • Um corte é um conjunto de arcos que define uma partição do conjunto de vértices [S, N-S], de maneira que cada arco pertencente ao corte possui um dos seus extremos em S e o outro em N-S. • Um corte s-t é um corte [S, N-S] com respeito a dois vértices s e t do grafo, de maneira que s S e t N-S. UFES

Árvores • Uma árvore é um grafo conexo sem ciclos. • Algumas propriedades: – Uma árvore com n nós possui exatamente n-1 arcos – Cada par de vértices de uma árvore está conectado por exatamente um único caminho – Uma árvore possui pelo menos 2 folhas (vértices de grau 1) • Uma floresta é um grafo sem ciclos. • Subárvore: um subgrafo conexo de uma árvore • Árvore enraizada: algum vértice da árvore é escolhido como raíz e todos os outros vértices são “hierarquizados” de acordo com essa raíz UFES

Árvores • Uma árvore out-tree direcionada enraizada no nó s é uma árvore T na qual o único caminho entre s e cada vértice de T é um caminho direcionado. • Uma árvore in-tree direcionada enraizada no nó s é uma árvore T na qual o único caminho entre cada vértice de T e s é um caminho direcionado. • Árvore geradora: Uma árvore T é uma árvore geradora de G se T é subgrafo gerador de G e é uma árvore. • Um grafo G é bipartido seu conjunto de vértices pode ser particionado em 2 conjuntos N 1 e N 2 de forma que cada arco de G possui um dos extremos em N 1 e o outro em N 2 e não há arcos que liguem vértices de uma mesma partição. – Propriedade: Um grafo G é bipartido sss cada ciclo em G possui comprimento par. UFES