Messy nice stuff Nice messy stuff Omri Barak

Messy nice stuff & Nice messy stuff Omri Barak Collaborators: Larry Abbott David Sussillo Misha Tsodyks Sloan-Swartz July 12, 2011

Neural representation • Representation of task parameters by neural population. • We know that large populations of neurons are involved. • Yet we look for and are inspired by impressive single neurons. • Case study: Delayed vibrotactile discrimination (from Ranulfo Romo’s lab)
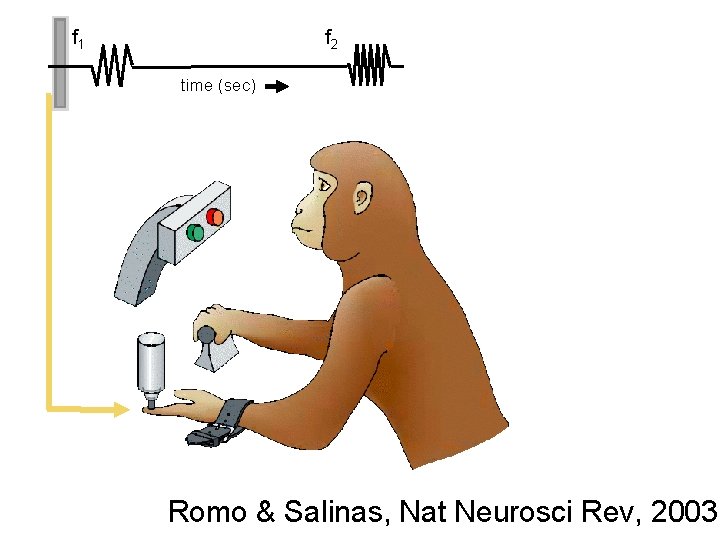
f 1 f 2 time (sec) Romo & Salinas, Nat Neurosci Rev, 2003
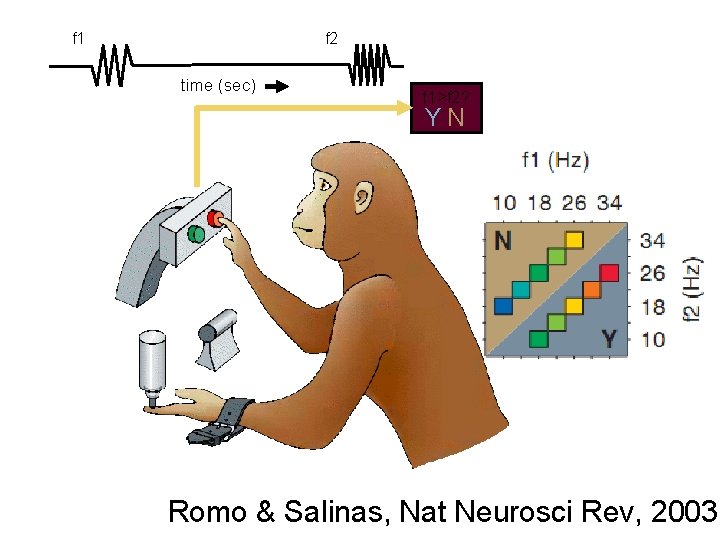
f 1 f 2 time (sec) f 1>f 2? YN Romo & Salinas, Nat Neurosci Rev, 2003

Romo task • Encoding of analog variable • Memory of analog variable • Arithmetic operation “f 1 -f 2”
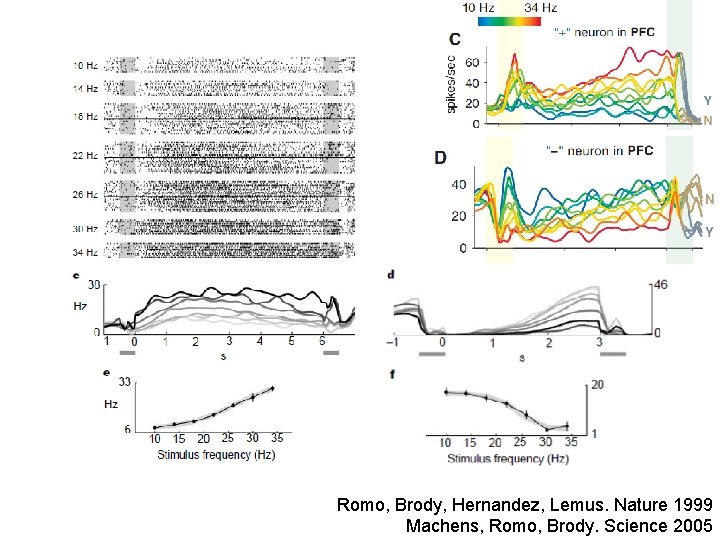
Romo, Brody, Hernandez, Lemus. Nature 1999 Machens, Romo, Brody. Science 2005

• Striking tuning properties • Lead to “simple / low dimensional” models • “Typical” neurons are used to define model populations.
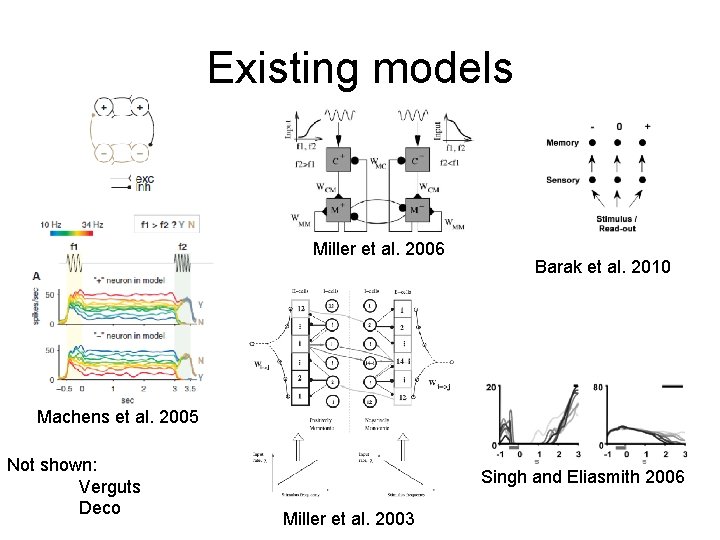
Existing models Miller et al. 2006 Barak et al. 2010 Machens et al. 2005 Not shown: Verguts Deco Singh and Eliasmith 2006 Miller et al. 2003
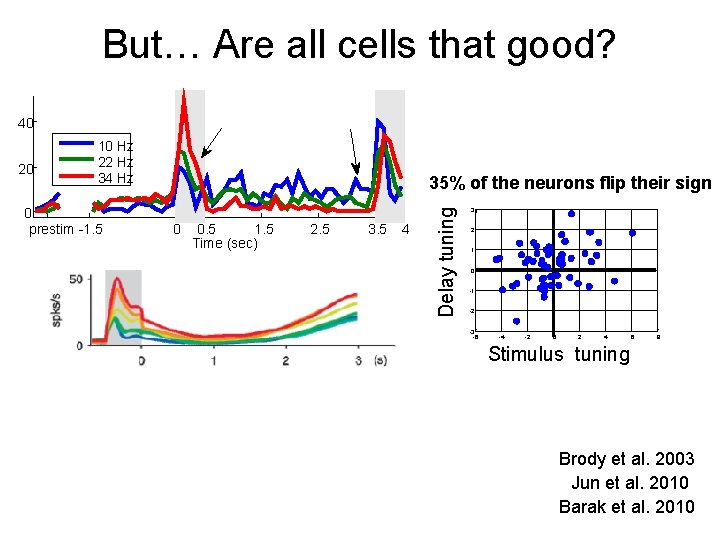
But… Are all cells that good? 40 0 prestim -1. 5 35% of the neurons flip their sign 0 0. 5 1. 5 Time (sec) 2. 5 3. 5 4 Delay tuning 20 10 Hz 22 Hz 34 Hz 3 2 1 0 -1 -2 -3 -6 -4 -2 0 2 4 6 8 Stimulus tuning Brody et al. 2003 Jun et al. 2010 Barak et al. 2010
Echo state network Jaeger 2001 Maass et al 2002 Buonomano and Merzenich 1995
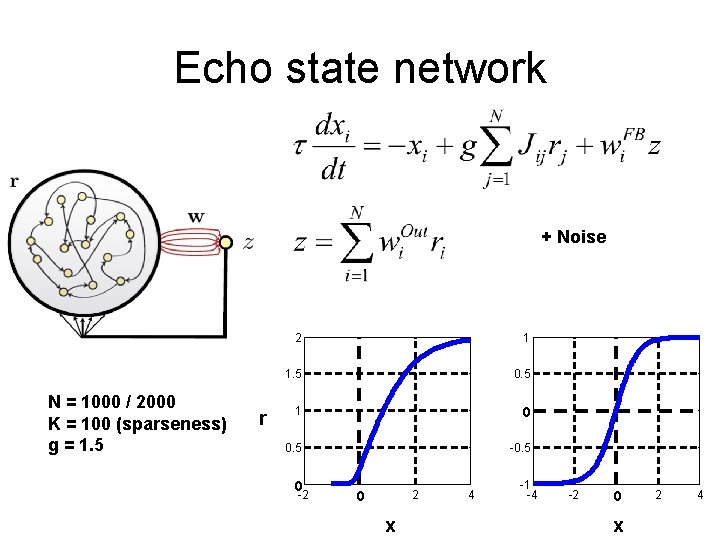
Echo state network + Noise N = 1000 / 2000 K = 100 (sparseness) g = 1. 5 r 2 1 1. 5 0. 5 1 0 0. 5 -0. 5 0 -2 2 0 x 4 -1 -4 -2 0 x 2 4
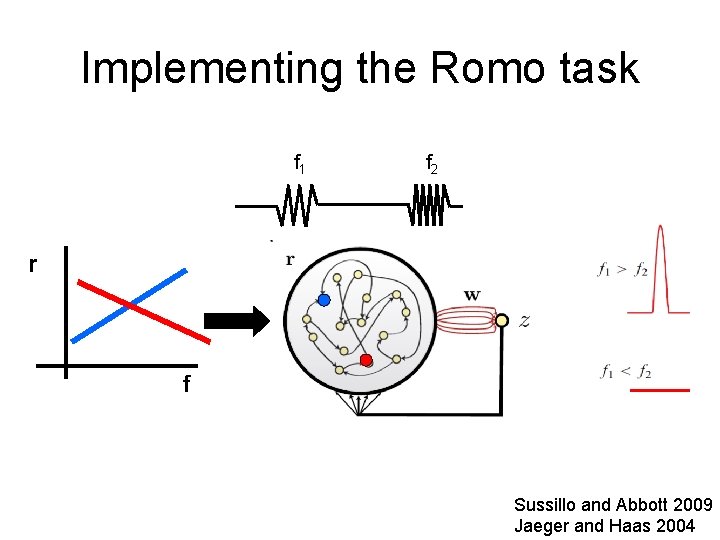
Implementing the Romo task f 1 f 2 r f Sussillo and Abbott 2009 Jaeger and Haas 2004
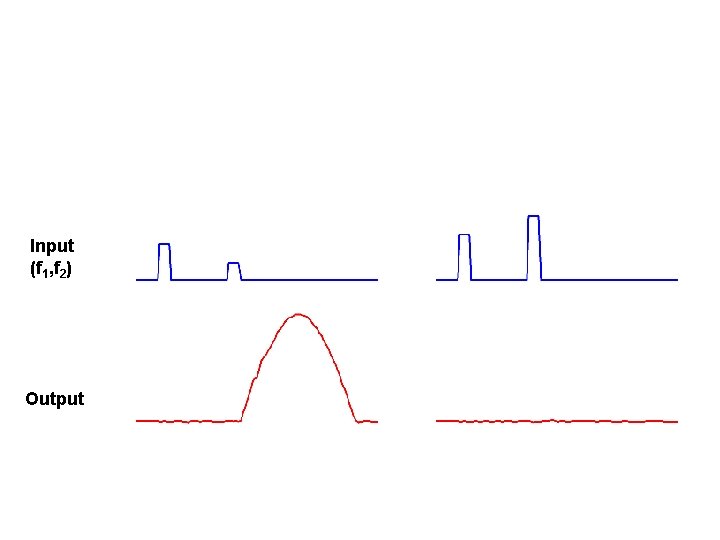
Input (f 1, f 2) Output
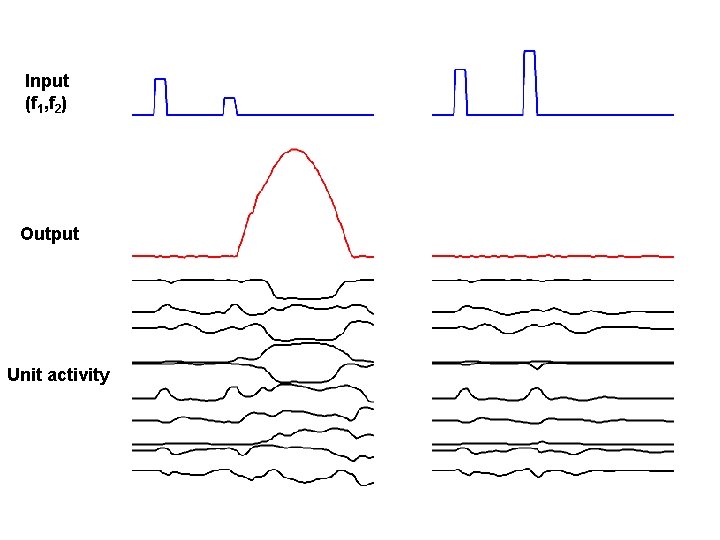
Input (f 1, f 2) Output Unit activity

It works, but… • How does it work? – After the training, we have a network that is almost a black box. • Relation to experimental data.

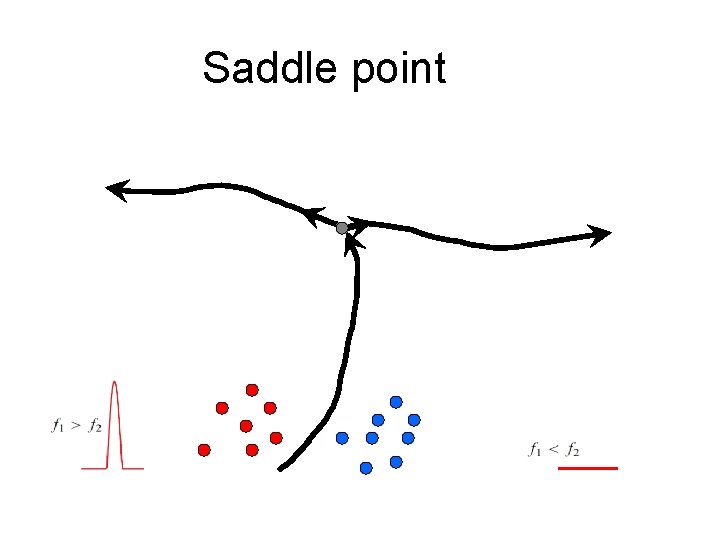
Hypothesis • Consider the state of the network in 1000 D as the trial evolves
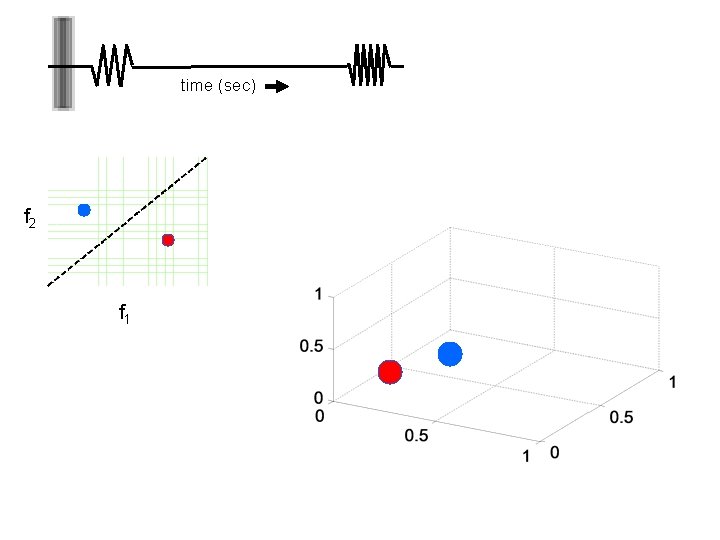
time (sec) f 2 f 1

Hypothesis • Focus only at the end of the 2 nd stimulus. • For each (f 1, f 2) pair, there is a point in 1000 -D space.


Hypothesis • Focus only at the end of the 2 nd stimulus. • For each (f 1, f 2) pair, there is a point in 1000 -D space. • So there is a 2 D manifold in the 1000 -D space. • Can the dynamics (after learning) draw a line through this manifold?

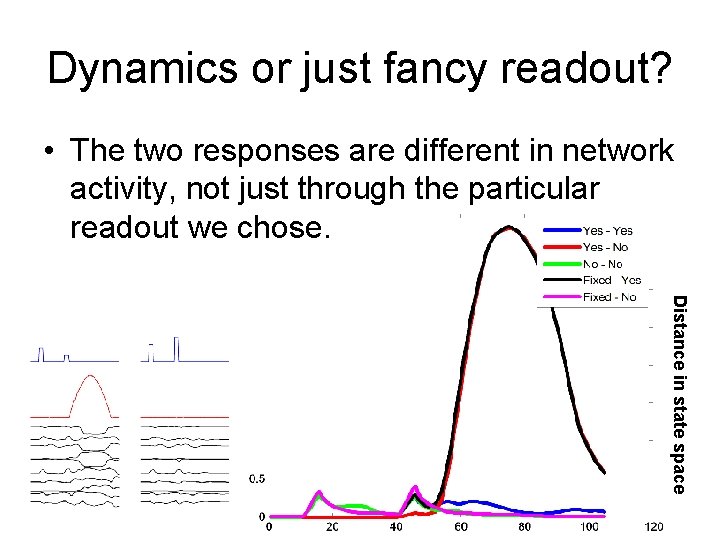
Dynamics or just fancy readout? • The two responses are different in network activity, not just through the particular readout we chose. Distance in state space
Saddle point

Searching for a saddle in 1000 D Vector function: Scalar function:
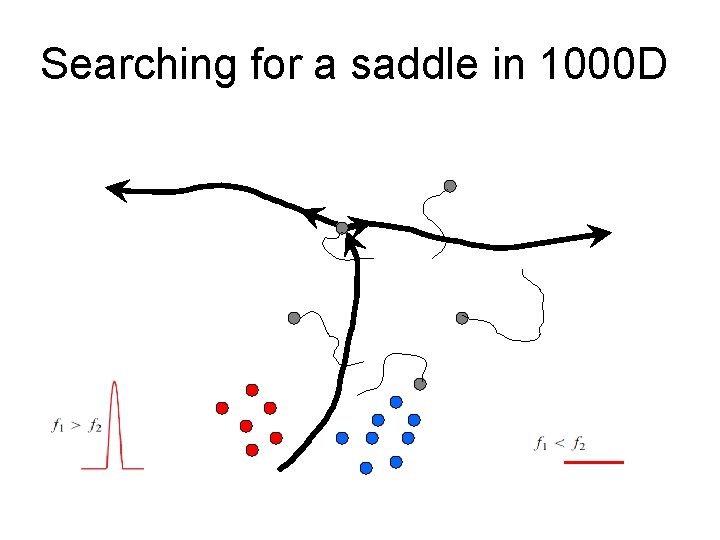
Searching for a saddle in 1000 D
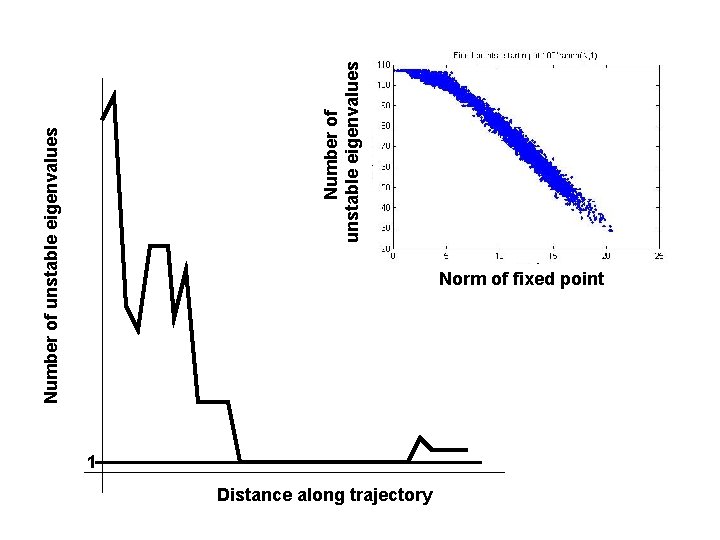
Number of unstable eigenvalues Norm of fixed point 1 Distance along trajectory
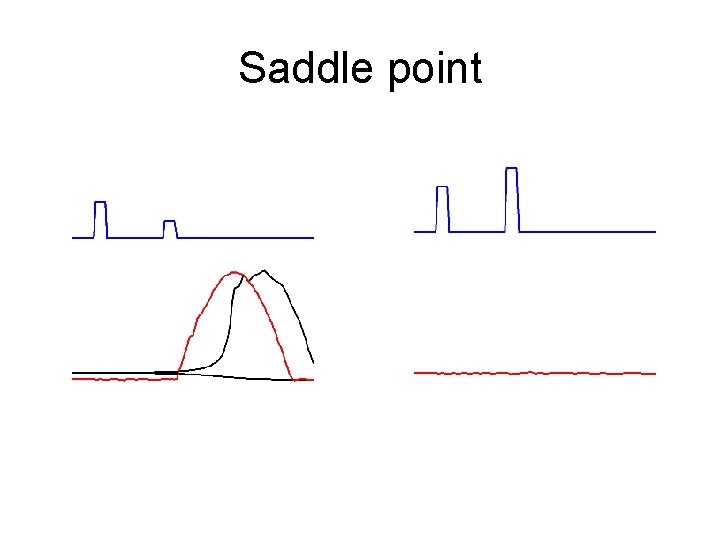
Saddle point
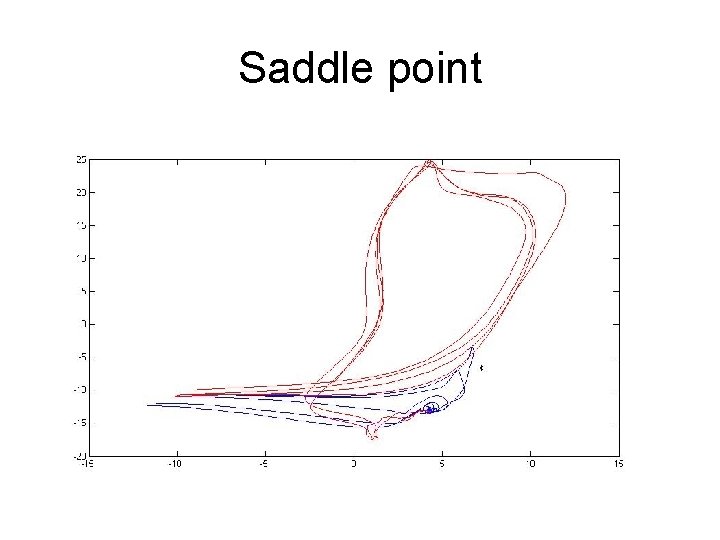
Saddle point

Slightly more realistic • • Positive firing rates Avoid fixed point between trials. Introduce reset signal. Chaotic activity in delay period =0

It works
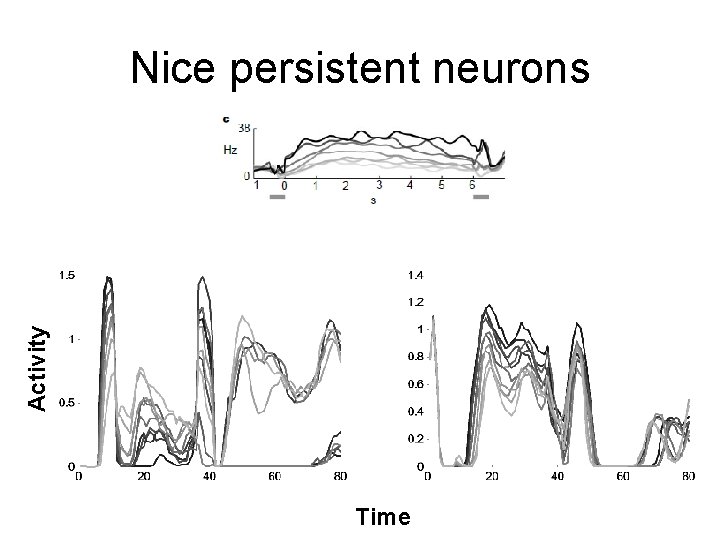
Activity Nice persistent neurons Time
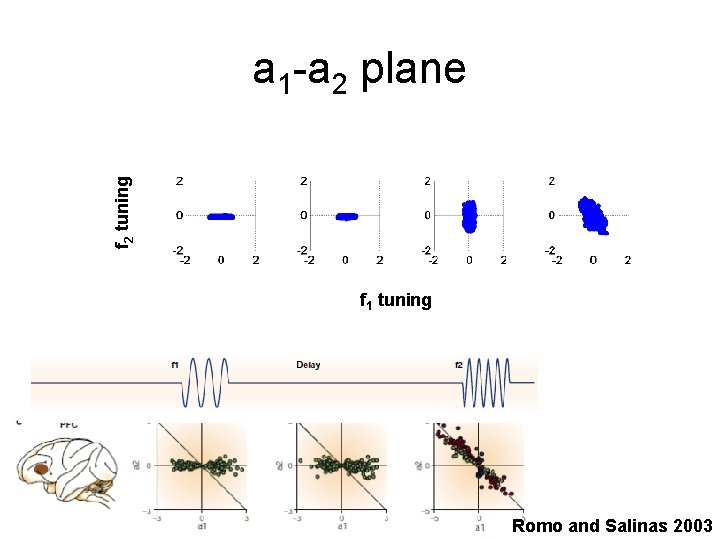
f 2 tuning a 1 -a 2 plane f 1 tuning Romo and Salinas 2003

Problems / predictions • Reset signal • Generalization
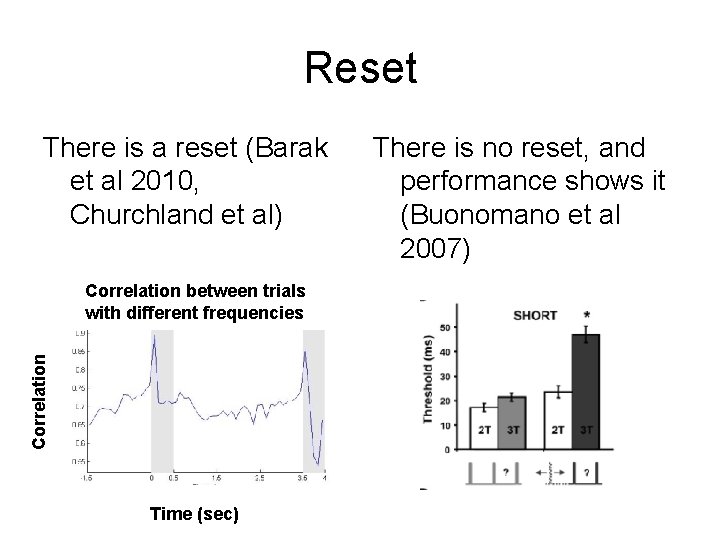
Reset There is a reset (Barak et al 2010, Churchland et al) Correlation between trials with different frequencies Time (sec) There is no reset, and performance shows it (Buonomano et al 2007)
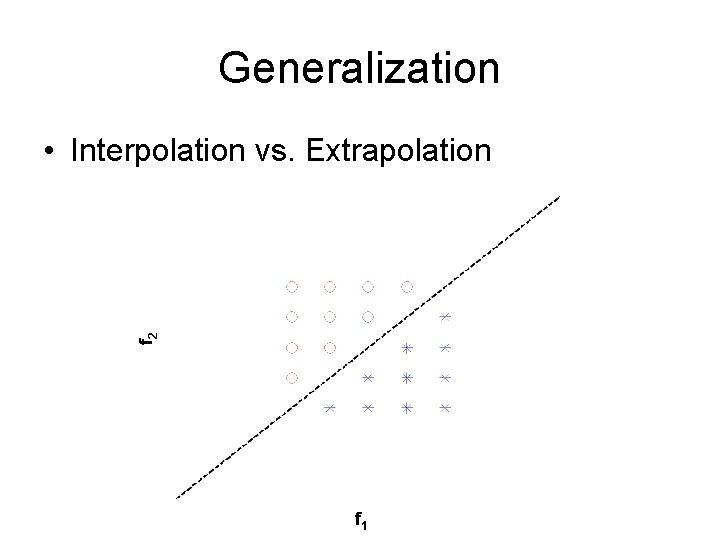
Generalization f 2 • Interpolation vs. Extrapolation f 1
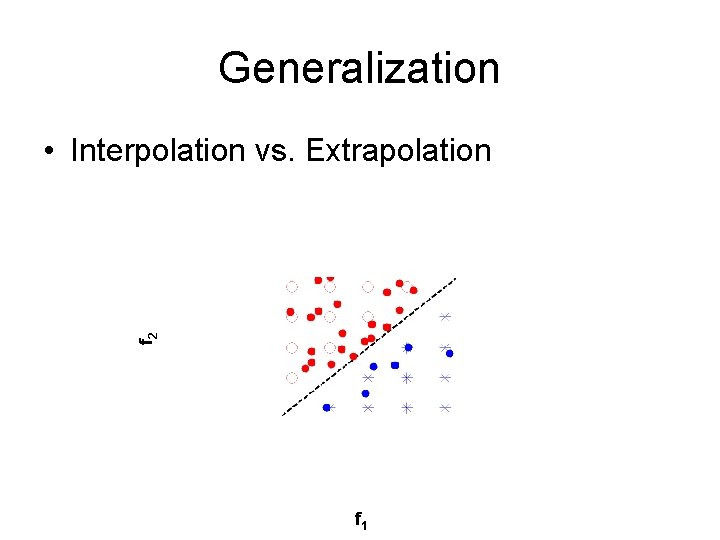
Generalization f 2 • Interpolation vs. Extrapolation f 1

Generalization f 2 • Interpolation vs. Extrapolation f 1

Extrapolation Delosh et al 1997

Conclusions • Response properties of individual neurons can be misleading. • An echo state network can solve decision making tasks. • Dynamical systems analysis can reveal function of echo state networks. • Need to find a middle ground.
- Slides: 39