Mesoscopic and Stochastic Phenomena and the Lac operon

Mesoscopic and Stochastic Phenomena and the Lac operon Ádám Halász joint work with Agung Julius, Vijay Kumar, George Pappas Adam Halasz Towards Systems Biology, October 2007, Grenoble

Outline • Lactose induction in E. coli, an example of bistability • Stochastic phenomena in reaction networks • Mesoscopic effects in the lac operon • Outlook Adam Halasz Towards Systems Biology, October 2007, Grenoble

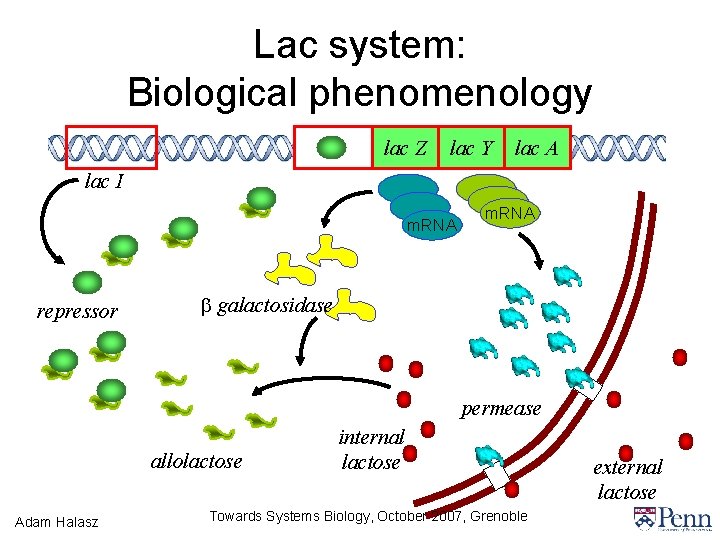
Lac system: Biological phenomenology lac Z lac Y lac A lac I m. RNA repressor m. RNA b galactosidase permease allolactose Adam Halasz internal lactose Towards Systems Biology, October 2007, Grenoble external lactose

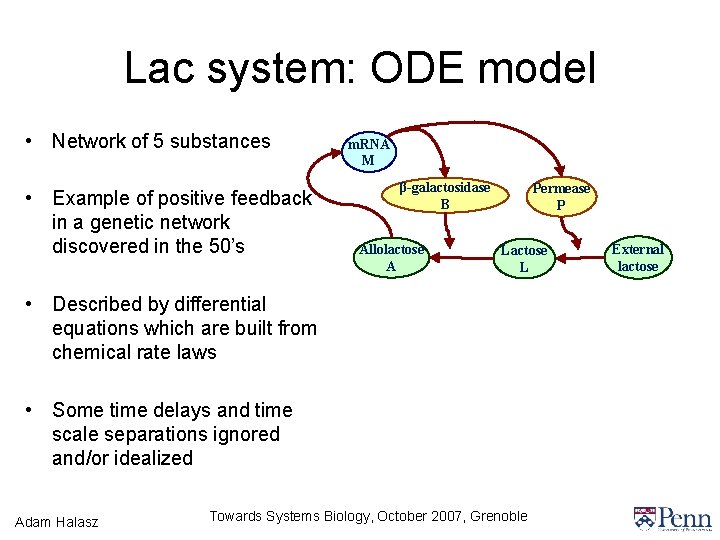
Lac system: ODE model • Network of 5 substances • Example of positive feedback in a genetic network discovered in the 50’s m. RNA M β-galactosidase B Allolactose A Permease P Lactose L • Described by differential equations which are built from chemical rate laws • Some time delays and time scale separations ignored and/or idealized Adam Halasz Towards Systems Biology, October 2007, Grenoble External lactose

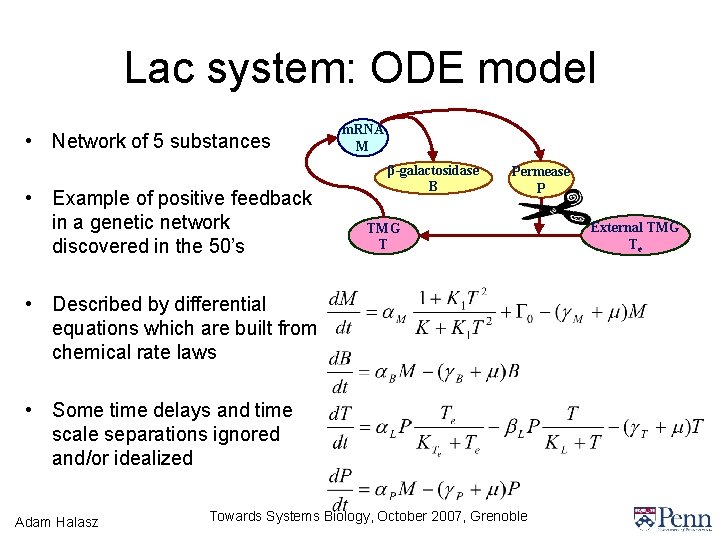
Lac system: ODE model • Network of 5 substances • Example of positive feedback in a genetic network discovered in the 50’s m. RNA M β-galactosidase B Permease P TMG T • Described by differential equations which are built from chemical rate laws • Some time delays and time scale separations ignored and/or idealized Adam Halasz Towards Systems Biology, October 2007, Grenoble External TMG Te

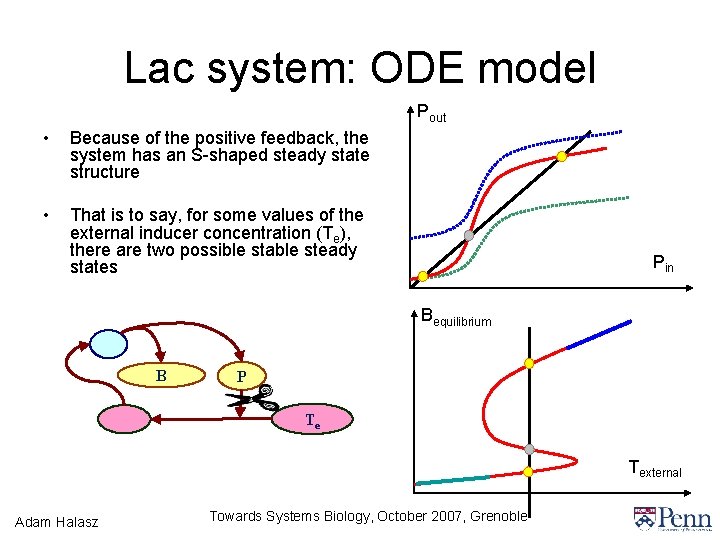
Lac system: ODE model Pout • Because of the positive feedback, the system has an S-shaped steady state structure • That is to say, for some values of the external inducer concentration (Te), there are two possible stable steady states Pin Bequilibrium B P Te Texternal Adam Halasz Towards Systems Biology, October 2007, Grenoble

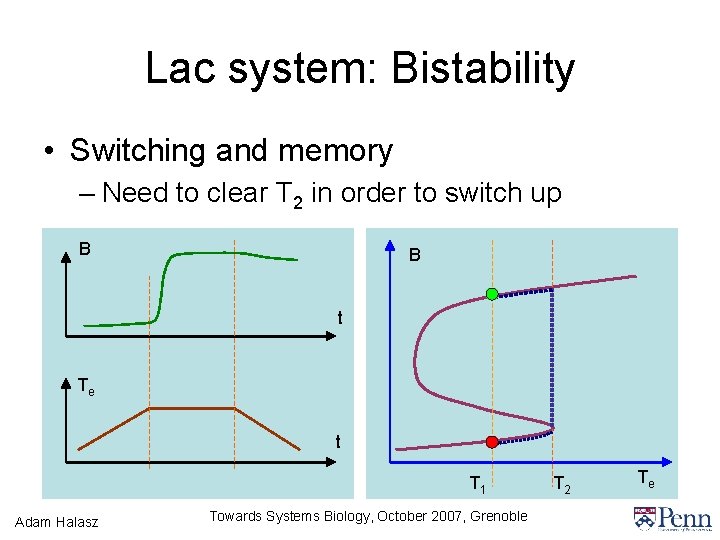
Lac system: Bistability • Switching and memory – Need to clear T 2 in order to switch up B B t Te t T 1 Adam Halasz Towards Systems Biology, October 2007, Grenoble T 2 Te

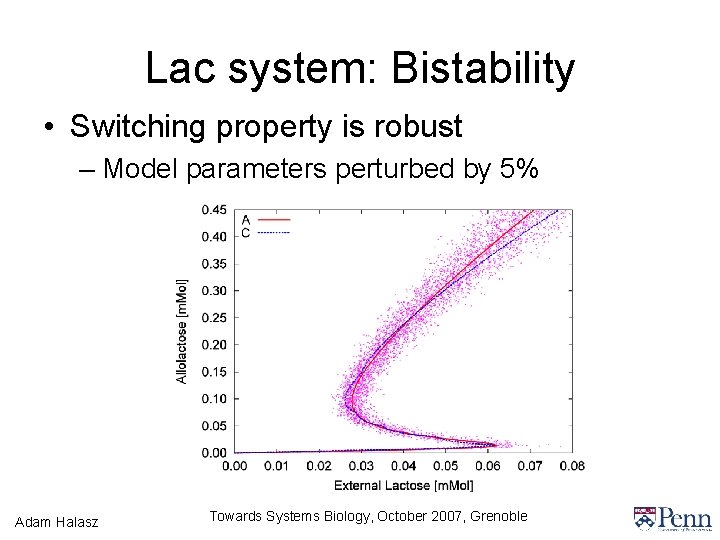
Lac system: Bistability • Switching property is robust – Model parameters perturbed by 5% Adam Halasz Towards Systems Biology, October 2007, Grenoble

Lac system – first lesson • Network of <5 species involved in reactions • Reactions decomposed* into mass action laws • Can be implemented using simple stochastic transition rules eg: “upon colliding with a B, A becomes C with probability x” • Recipe for synthesis of switch with hysteresis • Compose motifs to build logical functions, … – Design the network and transition rules – Map the rules to individual stochastic programs Adam Halasz Towards Systems Biology, October 2007, Grenoble

Lac system: ODE is not enough Adam Halasz Towards Systems Biology, October 2007, Grenoble

Stochastic versus deterministic • Substances are represented by finite numbers of molecules • Rate laws reflect the probability of individual molecular transitions • The abstraction/limit process is not always trivial Next transition time distribution: t 1 N 1 Adam Halasz t 2 N 2=N 1 -2 Towards Systems Biology, October 2007, Grenoble :

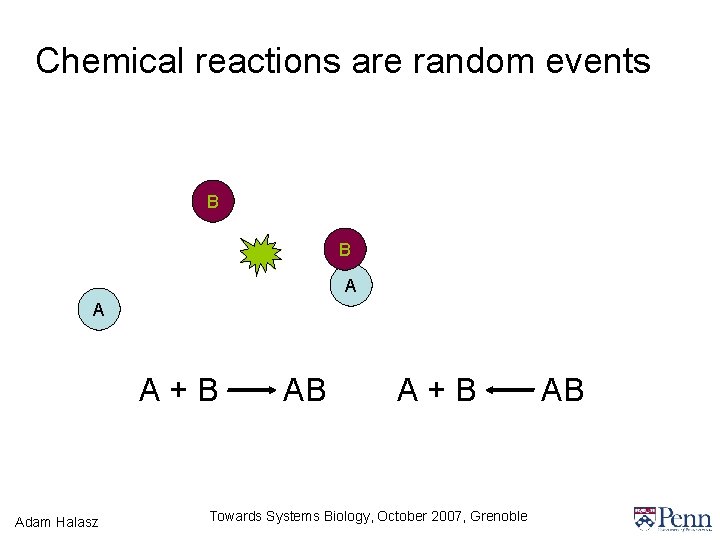
Chemical reactions are random events B B A A A+B Adam Halasz AB A+B Towards Systems Biology, October 2007, Grenoble AB

Stochastic reaction kinetics • Quantities are measured as #molecules instead of concentration. • Reaction rates are seen as rates of Poisson processes. k • A + B AB Rate of Poisson process Adam Halasz Towards Systems Biology, October 2007, Grenoble

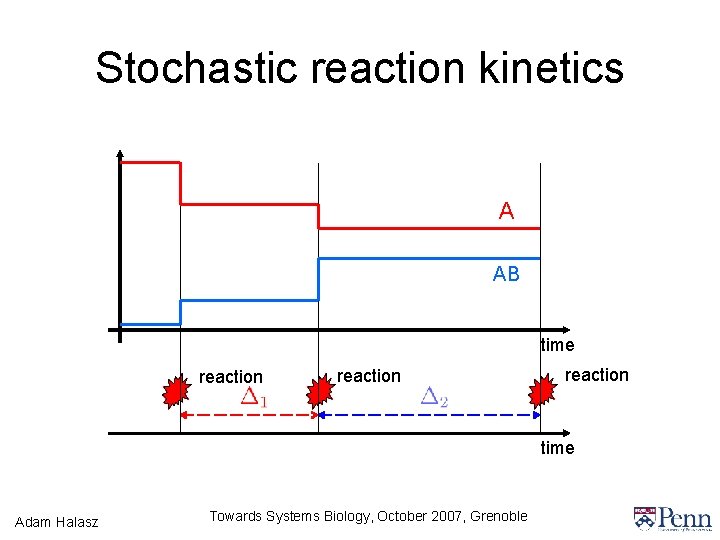
Stochastic reaction kinetics A AB time reaction time Adam Halasz Towards Systems Biology, October 2007, Grenoble

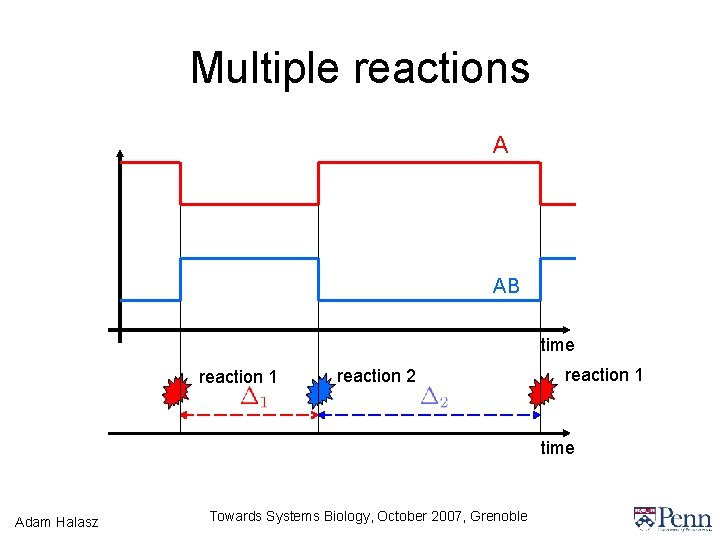
Multiple reactions • Multiple reactions are seen as concurrent Poisson processes. k 1 A + B AB k 2 Rate 1 Rate 2 • Gillespie simulation algorithm: determine which reaction happens first. Adam Halasz Towards Systems Biology, October 2007, Grenoble

Multiple reactions A AB time reaction 1 reaction 2 reaction 1 time Adam Halasz Towards Systems Biology, October 2007, Grenoble

Gillespie simulations • When the number of molecules per cell is small*, the respective substance has to be treated as an integer variable • The probabilistic transition rules can be implemented in standard ways • Gillespie method: instead of calculating time derivatives, we calculate the time of the next transition • Many other sophisticated methods exist. As an empirical rule, the higher the number of molecules, the closer the simulation is to the continuous version Adam Halasz Towards Systems Biology, October 2007, Grenoble

Gillespie automata • The state of the system is given by the number of copies of each molecular species • Transitions consist of copy number changes corresponding to elementary reactions • The distribution of the next transition time is Poisson, e-kt where k is the propensity • A Gillespie automaton is a mathematical concept [a continuous time Markov chain] • Plays the same role differential equations have in the continuum description Adam Halasz Towards Systems Biology, October 2007, Grenoble

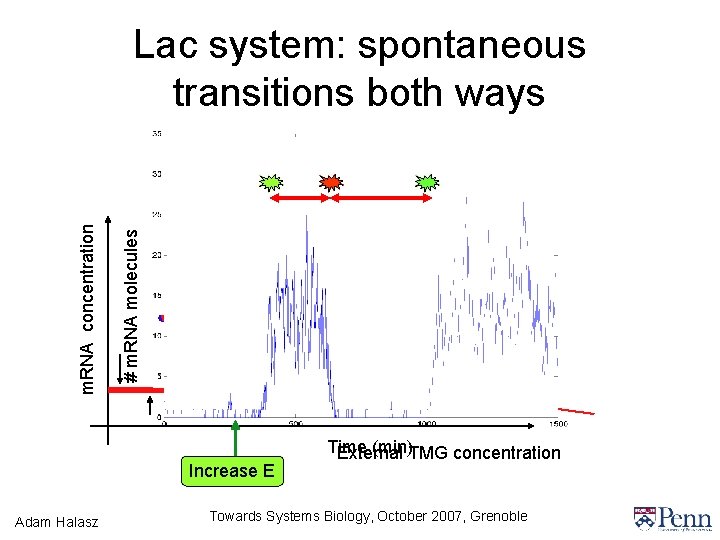
# m. RNA molecules m. RNA concentration Lac system: spontaneous transitions both ways Increase E Adam Halasz Time (min)TMG concentration External Towards Systems Biology, October 2007, Grenoble

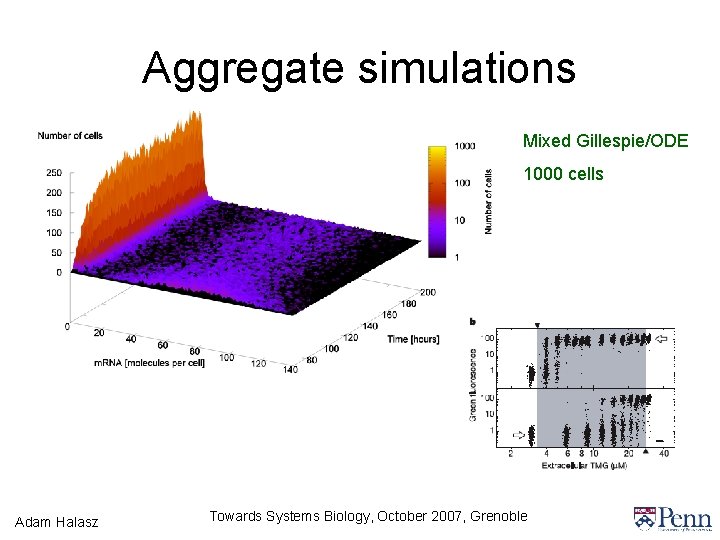
Aggregate simulations Mixed Gillespie/ODE 1000 cells Adam Halasz Towards Systems Biology, October 2007, Grenoble

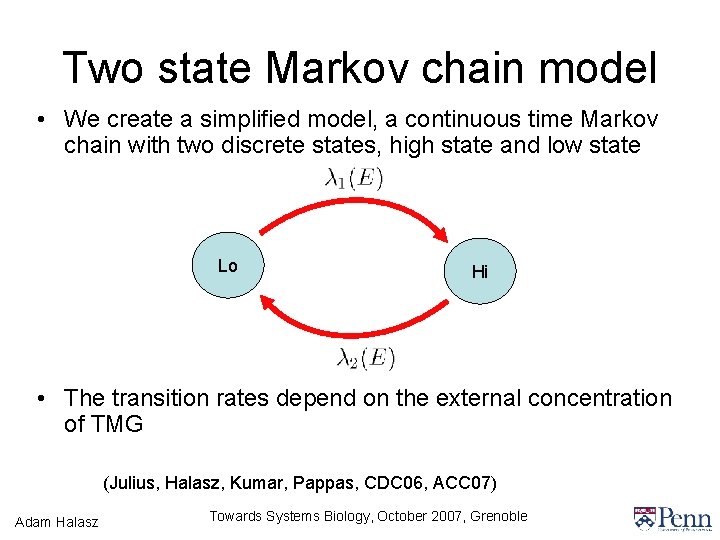
Two state Markov chain model • We create a simplified model, a continuous time Markov chain with two discrete states, high state and low state Lo Hi • The transition rates depend on the external concentration of TMG (Julius, Halasz, Kumar, Pappas, CDC 06, ACC 07) Adam Halasz Towards Systems Biology, October 2007, Grenoble

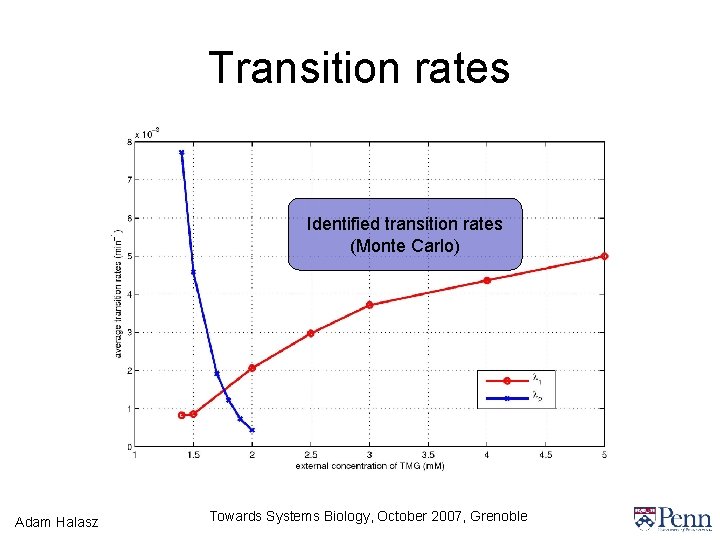
Transition rates Identified transition rates (Monte Carlo) Adam Halasz Towards Systems Biology, October 2007, Grenoble

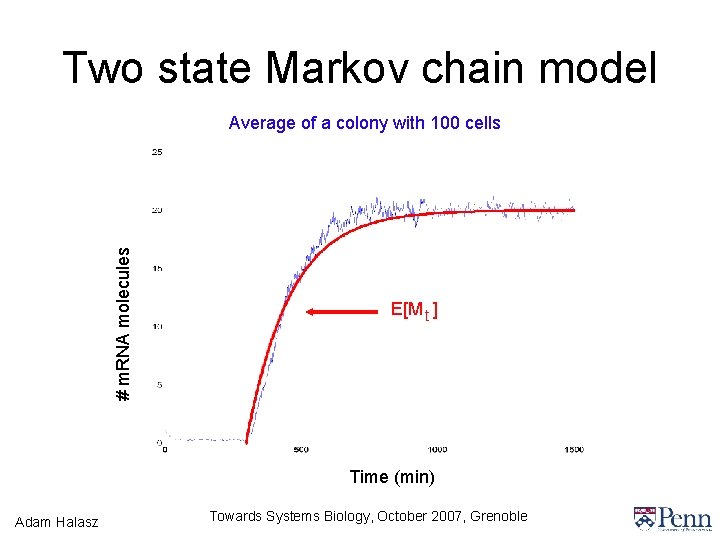
Two state Markov chain model # m. RNA molecules Average of a colony with 100 cells E[M t ] Time (min) Adam Halasz Towards Systems Biology, October 2007, Grenoble

Lac system – second lesson • Bad news: underlying stochasticity can drastically modify the ODE prediction – The price paid for an ‘uncontrolled’ approximation • Good news: the ODE abstraction can also be performed rigorously – Gillespie automaton is an exact abstraction – For Gillespie ODE, all ‘molecule’ numbers must be large • Stochastic effects retained at the macro-discrete level – Effects are reproducible and quantifiable – Further abstractions of stochastic effects are possible • Lac example: can quantify the spontaneous transitions: – Choose an implementation where they are kept at a low rate – Implement control strategies that use the two-state model Adam Halasz Towards Systems Biology, October 2007, Grenoble

Beyond Gillespie • Gillespie method is ‘exact’ – produces exact realisations of the stochastic process • Main problem is computational cost – Larger molecule numbers – Rare transitions • Several approaches to circumvent ‘exact’ simulations Adam Halasz Towards Systems Biology, October 2007, Grenoble

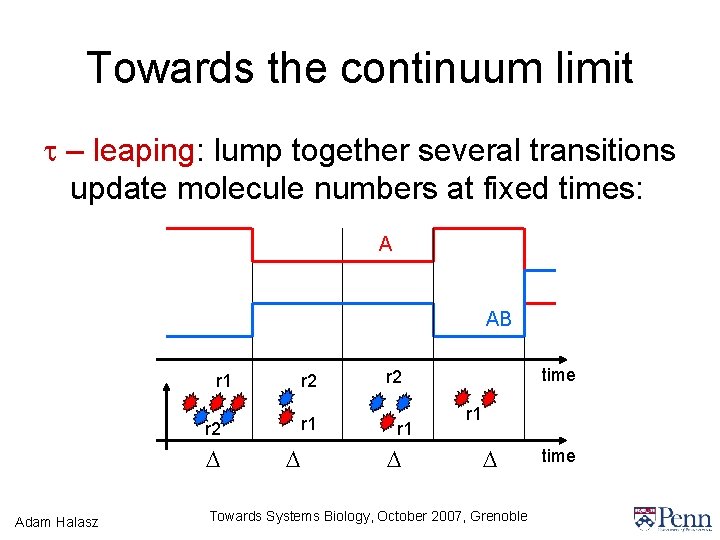
Towards the continuum limit t – leaping: lump together several transitions update molecule numbers at fixed times: A AB r 1 r 2 D Adam Halasz D time r 2 r 1 D Towards Systems Biology, October 2007, Grenoble time

Towards the continuum limit • Error introduced by t – leaping is due to variation of the propensities over the time interval (may lead to negative particle numbers!) • Acceptable if the expected relative change of each particle number over Δ is small (e. g. if the number of particles is large) • If the number of transitions per interval is also large, the variation can be described as a continuous random number stochastic differential equations • Finally, is the variance of the change per interval can also be neglected, the simulation is equivalent to an Euler scheme for an ODE. Adam Halasz Towards Systems Biology, October 2007, Grenoble

Other limiting cases • If the number of all possible configurations is relatively small, probabilities for each state can be calculated directly, by calculating all possible transition rates, (finite state projection) or using the master equation (Hespanha, Khammash, . . ) • In some situations (eg. signaling cascades) there is a combinatorial explosion of species, where agentbased simulations are useful (Los Alamos group, Kholodenko) Adam Halasz Towards Systems Biology, October 2007, Grenoble

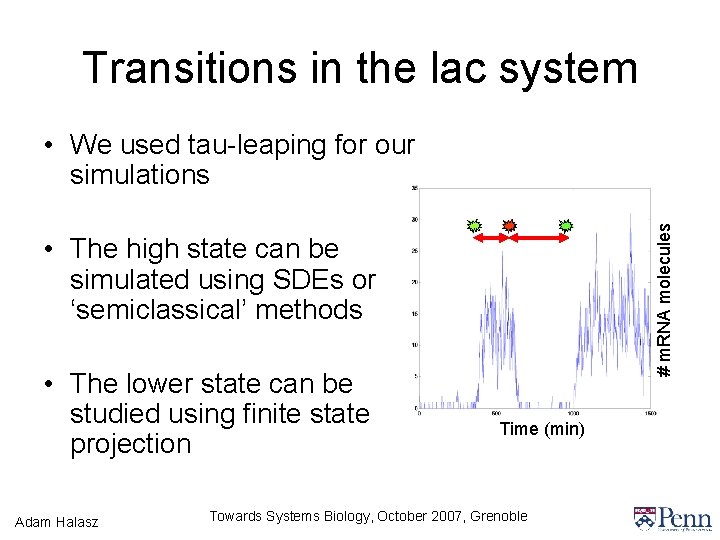
Transitions in the lac system # m. RNA molecules • We used tau-leaping for our simulations • The high state can be simulated using SDEs or ‘semiclassical’ methods • The lower state can be studied using finite state projection Adam Halasz Time (min) Towards Systems Biology, October 2007, Grenoble

Summary • Mesoscopic effects in biological reaction networks are due to small numbers of molecules in individual cells • They may affect the system dramatically, somewhat, or not at all • These effects can be described mathematically and incorporated in our modeling efforts • Several sophisticated methods exist; it is important to use an approximation that is appropriate, both in terms of correctness and in terms of efficiency Adam Halasz Towards Systems Biology, October 2007, Grenoble

Thanks: Agung Julius, , George Pappas, Vijay Kumar, Harvey Rubin DARPA, NIH, NSF, Penn Genomics Institute Adam Halasz Towards Systems Biology, October 2007, Grenoble