Mesh Parameterization Theory and Practice Setting the Boundary

Mesh Parameterization: Theory and Practice Setting the Boundary Free Bruno Lévy - INRIA

Overview 1. Introduction - Motivations 2. Using differential geometry 3. Analytic methods 4. Conclusion

1. Introduction Setting the bndy free, why ? Floater-Tutte: provably correct result for fixed convex boundary n

1. Introduction Seamster [Sheffer et. al] Cuts the model, ready for "pelting"

1. Introduction Fixed boundary - distortion

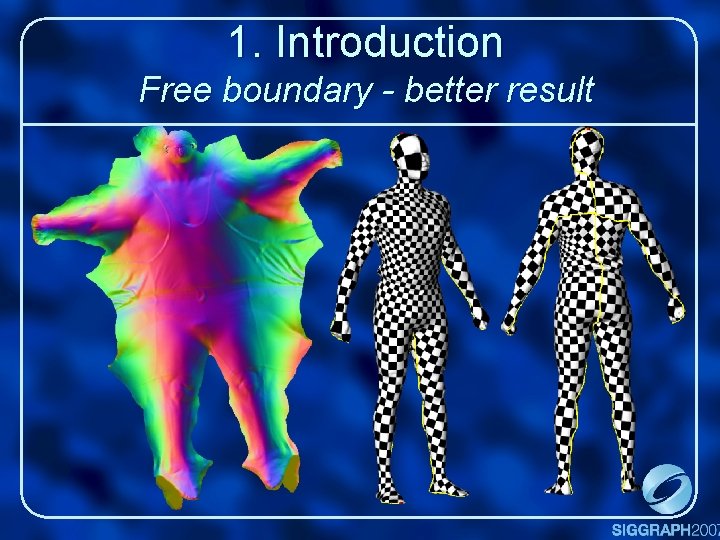
1. Introduction Free boundary - better result

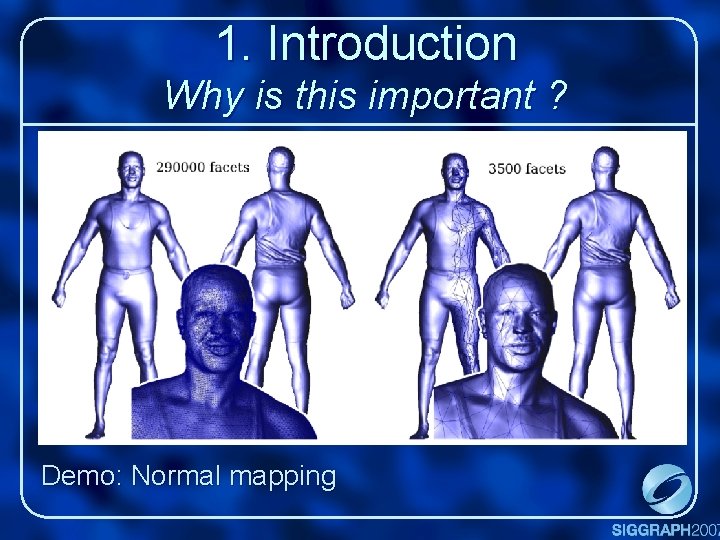
1. Introduction Why is this important ? Demo: Normal mapping

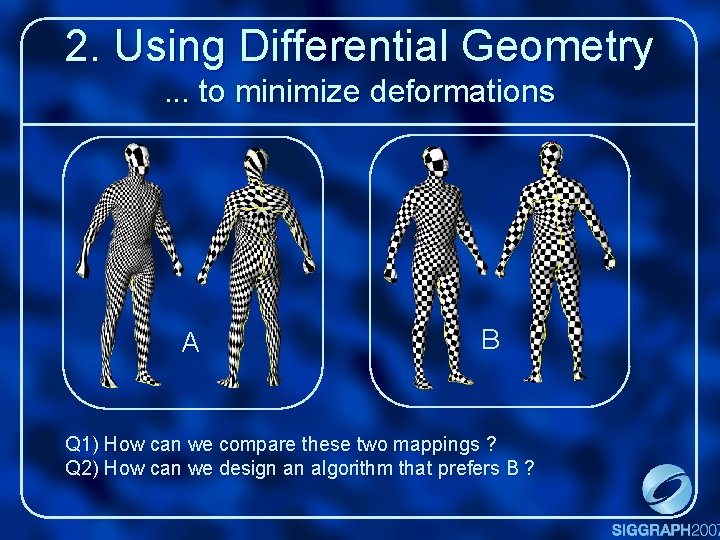
2. Using Differential Geometry. . . to minimize deformations A B Q 1) How can we compare these two mappings ? Q 2) How can we design an algorithm that prefers B ?

2. Using Differential Geometry. . . to minimize deformations [Greiner et. al]: Variational principles for geometric modeling with Splines PDEs for geometric optimization n Can we port this principle to the discrete setting ?

2. Using Differential Geometry. . . to minimize deformations [Hormann and Greiner] MIPS n [Pinkall and Poltier] cotan formula n [Do Carmo] for meshes

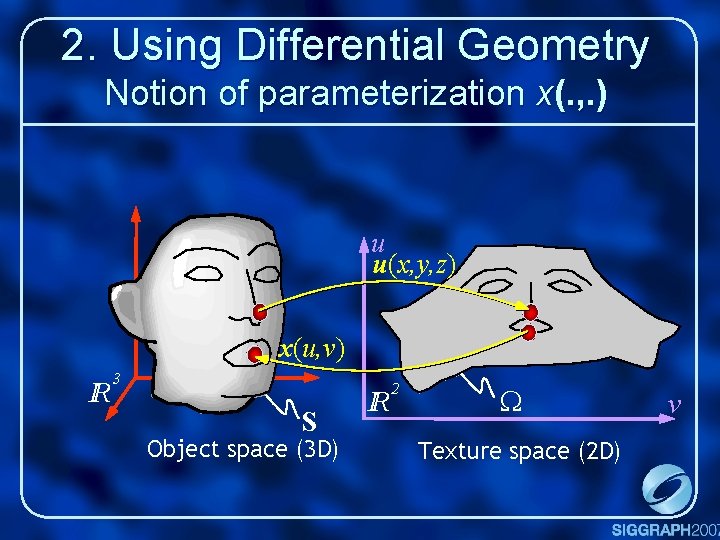
2. Using Differential Geometry Notion of parameterization x(. , . ) u u(x, y, z) x(u, v) IR 3 S Object space (3 D) IR 2 W Texture space (2 D) v

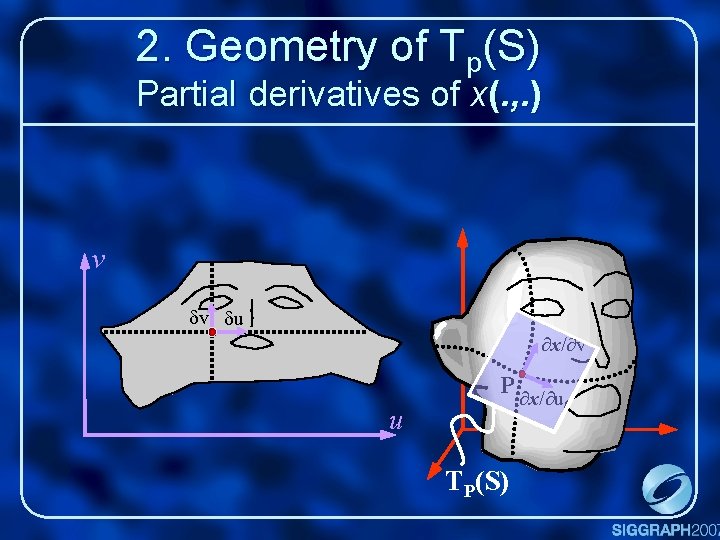
2. Geometry of Tp(S) Partial derivatives of x(. , . ) v dv du x/ v u P x/ u TP(S)

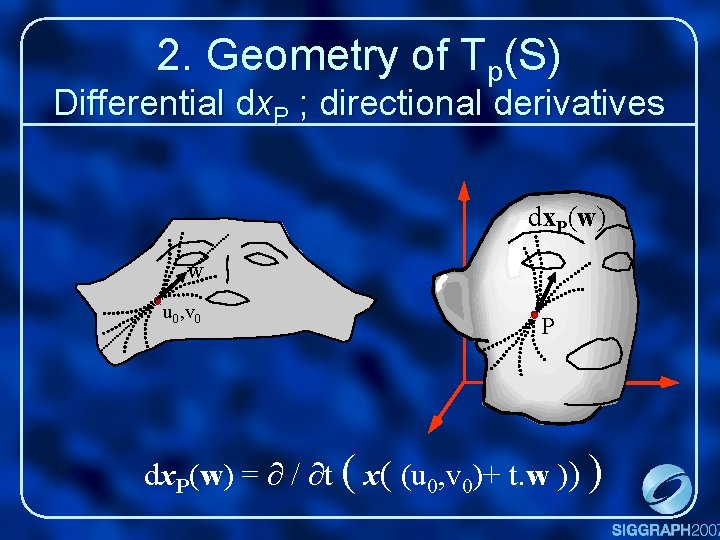
2. Geometry of Tp(S) Differential dx. P ; directional derivatives dx. P(w) w u 0, v 0 P dx. P(w) = / t ( x( (u 0, v 0)+ t. w )) )

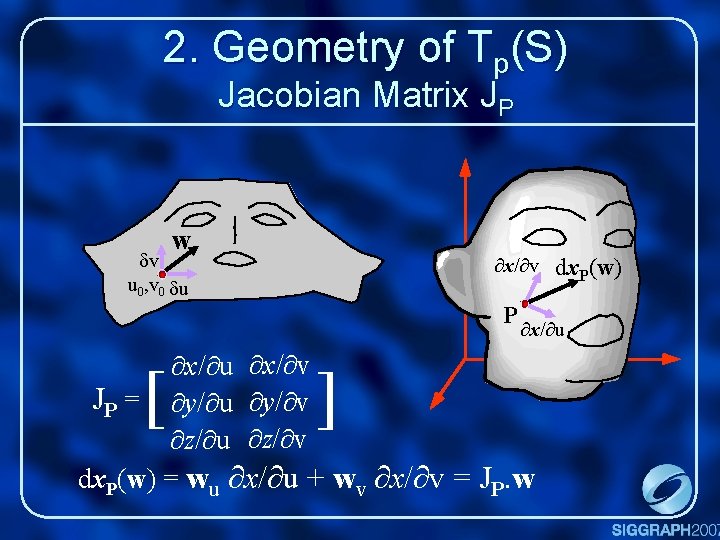
2. Geometry of Tp(S) Jacobian Matrix JP w dv u 0, v 0 du x/ v P x/ u x/ v JP = y/ u y/ v z/ u z/ v dx. P(w) = wu x/ u + wv x/ v = JP. w [ ] dx. P(w)

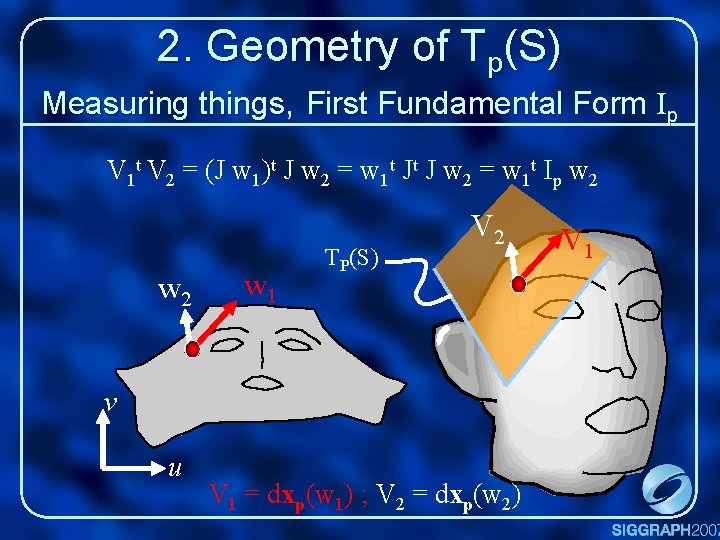
2. Geometry of Tp(S) Measuring things, First Fundamental Form Ip V 1 t V 2 = (J w 1)t J w 2 = w 1 t Jt J w 2 = w 1 t Ip w 2 w 1 TP(S) V 2 v u V 1 = dxp(w 1) ; V 2 = dxp(w 2) V 1

2. Geometry of Tp(S) Measuring things, First Fundamental Form Ip Distances : || V 1 ||2 = w 1 t Ip w 1 Angles : V 1 t V 2 = w 1 t Ip w 2 Ip is called the metric tensor

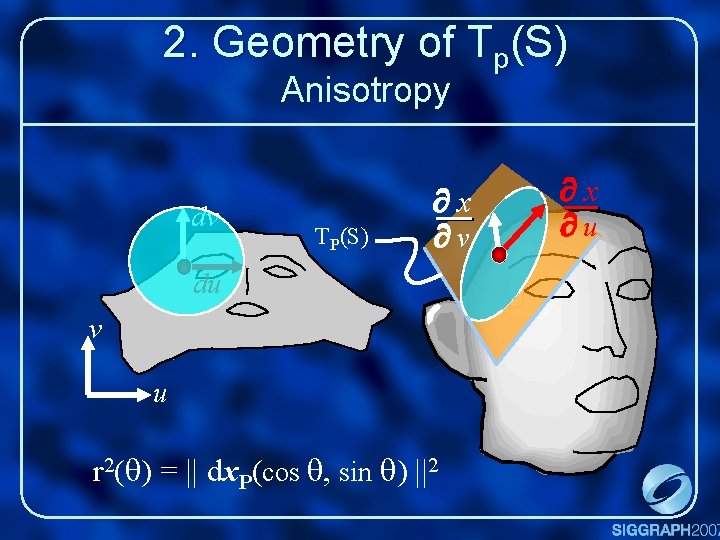
2. Geometry of Tp(S) Anisotropy dv TP(S) x v du v u r 2(q) = || dx. P(cos q, sin q) ||2 x u

2. Geometry of Tp(S) Anisotropy ; 1 st fundamental form IP || dx. P(w) ||2 = || JP. w ||2 IP = x u 2 x v = (JPw)t x u x v 2 = wt. JP. w = wt. IP. w

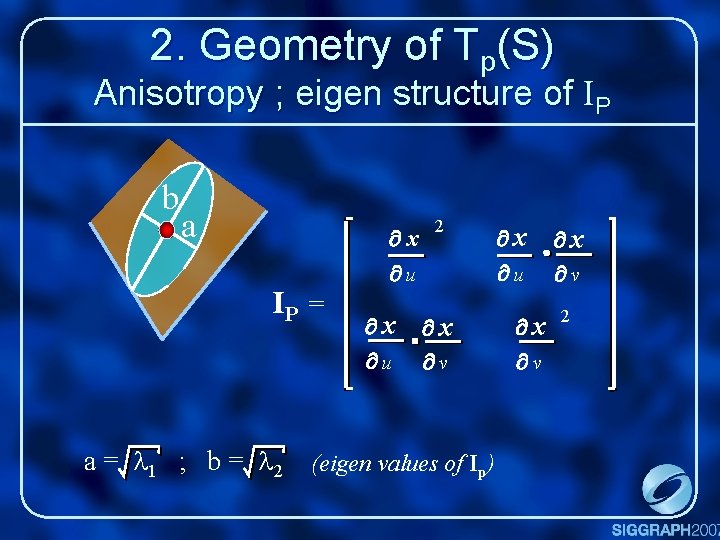
2. Geometry of Tp(S) Anisotropy ; eigen structure of IP b a IP = a = l 1 ; b = l 2 x u 2 x v (eigen values of Ip) x u x v 2

2. Geometry of Tp(S) Anisotropy ; eigen structure of IP b a Jp = x u y u z u x v y v z v a 0 =U 0 b Vt 0 0 Singular values decomposition (SVD) of J Rem: Ip = Jt. J a = l 1 ; b = l 2

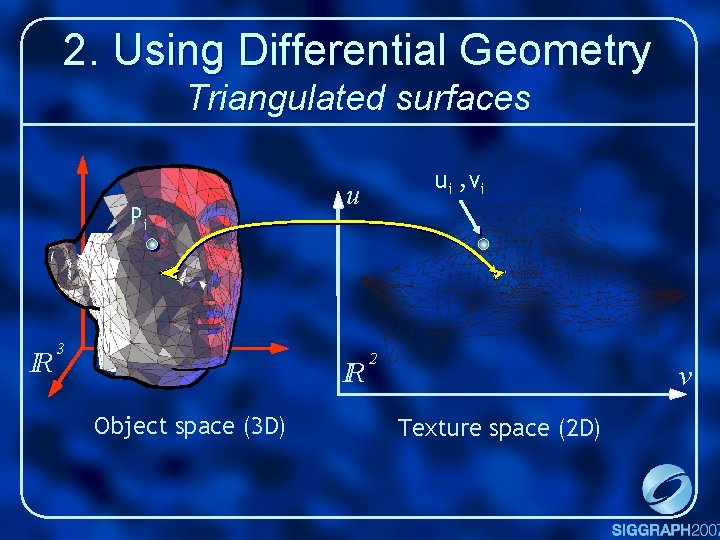
2. Using Differential Geometry Triangulated surfaces Pi IR 3 u IR Object space (3 D) ui , vi 2 v Texture space (2 D)

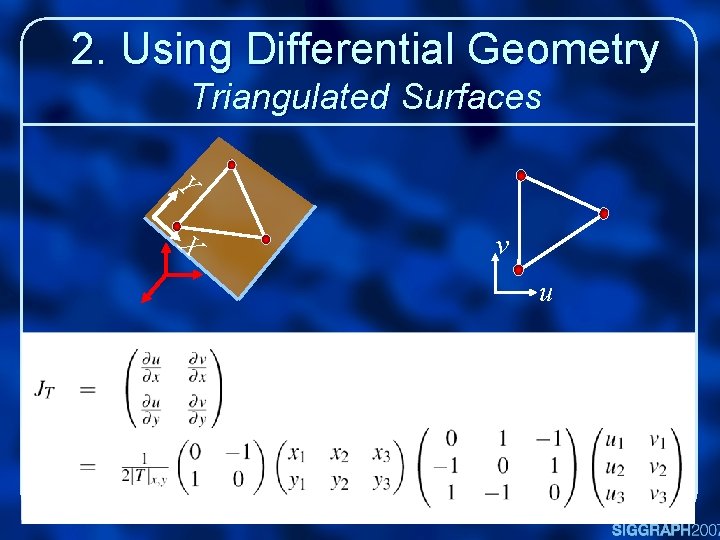
2. Using Differential Geometry Triangulated Surfaces Y X v u

2. Using Differential Geometry Anisotropy - See Kai's diff. geo. primer n first fundamental form n eigenvalues of n singular values of (anisotropy ellipse axes)

3. Analytic methods General Principle n Define some energy functional F in function of Jp, Ip, l 1, l 2 n Expand their expression in F in function of the unknown ui, vi n Design an algorithm to find the ui, vi's that minimizes F

3. Analytic methods The first fundamental form I is the metric tensor Minimize a matrix norm of I - Id [Maillot, Yahia & Verroust, 1993]

3. Analytic methods MIPS [Hormann et. al] Principle: F should be invariant by similarity and shoud punish collapsing triangles [Hormann & Greiner]

3. Analytic methods Stretch optimization [Sander et. al] w(q) dx. P(w(q)) TP(S) v u r 2(q) = ||dxp(w(q))||2 = || dx. P(cos q, sin q) ||2 Stretch L 2 = 1/2 p ∫ r 2(q)dq L∞ = max(r(q))

3. Analytic methods Stretch optimization [Sander et. al]

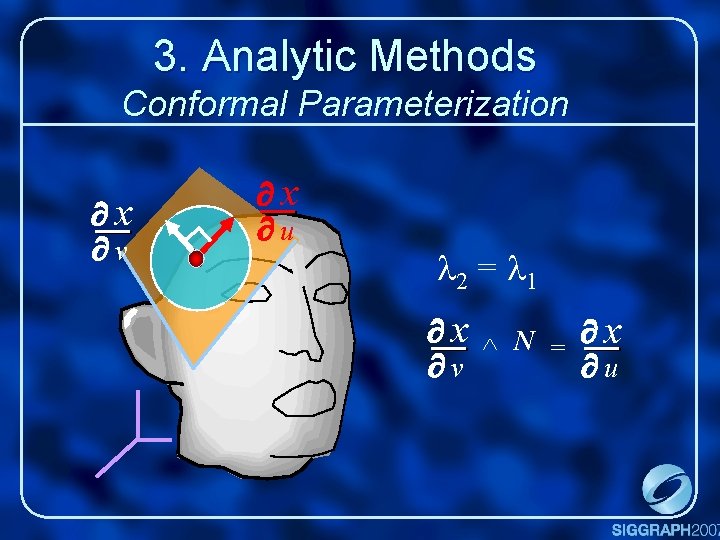
3. Analytic Methods Conformal Parameterization x v x u l 2 = l 1 x N = x ^ v u

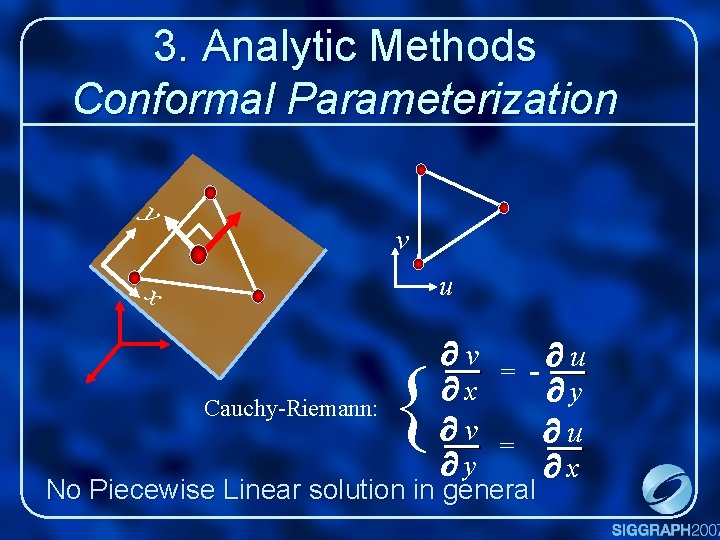
3. Analytic Methods Conformal Parameterization y v u x Cauchy-Riemann: { v u = x y v u = y x No Piecewise Linear solution in general

3. Analytic Methods LSCM [Levy et. al] Minimize S T v x v y - u - y u x 2 Fix two vertices to determine rot, transl, scaling + easy to implement - overlaps, deformations

3. Analytic Methods DNCP [Desbrun et. al] Tutte-Floater with harmonic weights (cotan) + additional equation for natural boundaries Bndry point i, grad of Dirichlet energy Natural idea for "setting the bndry free" (Laplace eqn with Neumman bndry)

Isotropic Parameterizations Conformal = Harmonic EC(u) + Au(T) = ED(u) = ½. | Au(T) = D where: u |2 det(Ju) Dirichlet Energy Area of T EC(u) = ½. || D 90( u) - v ||2 Conformal Energy [Douglas 31] [Rado 30] [Courant 50] [Brakke 90]

Application of free boundaries Show 2 D domain Segmentation: VSA [Alliez et. al]

Epilogue Limits of analytic methods LSCM ; DNCP distortions ; validity Geometric methods

Resources n Source code & papers on http: //alice. loria. fr – Graphite – Open. NL

Calls for papers n Eurographics 2008 – Abstracts: Sept 21, papers: Sept 26 n SPM / SPMI 2008 – Abstracts: Nov 27, papers: Dec 4 n SGP 2008 – Abstracts: April 20, papers: April 27 n Special issue Computing - eigenfunctions – Abstracts: Nov 1 st, Papers: Nov, 15 Paper copies of Cf. P available, ask us !

Course Evaluations 4 Random Individuals will win an ATI Radeontm HD 2900 XT http: //www. siggraph. org/course_evaluation